2021秋北师版九上数学4.7相似三角形的性质导学案(无答案)
文档属性
| 名称 | 2021秋北师版九上数学4.7相似三角形的性质导学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 230.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 00:00:00 | ||
图片预览


文档简介
2021秋北师版九上数学4.7相似三角形的性质导学案
第2课时
学习目标:
1.理解并掌握相似三角形对应高的比、对应角平分线的比、和对应中线的比都等于相似比;
2.应用相似三角形的性质进行证明和计算;
重点和难点:
重点:利用相似三角形的性质解决计算问题。
难点:相似三角形的性质定理的证明。
学习过程:
一、学习准备
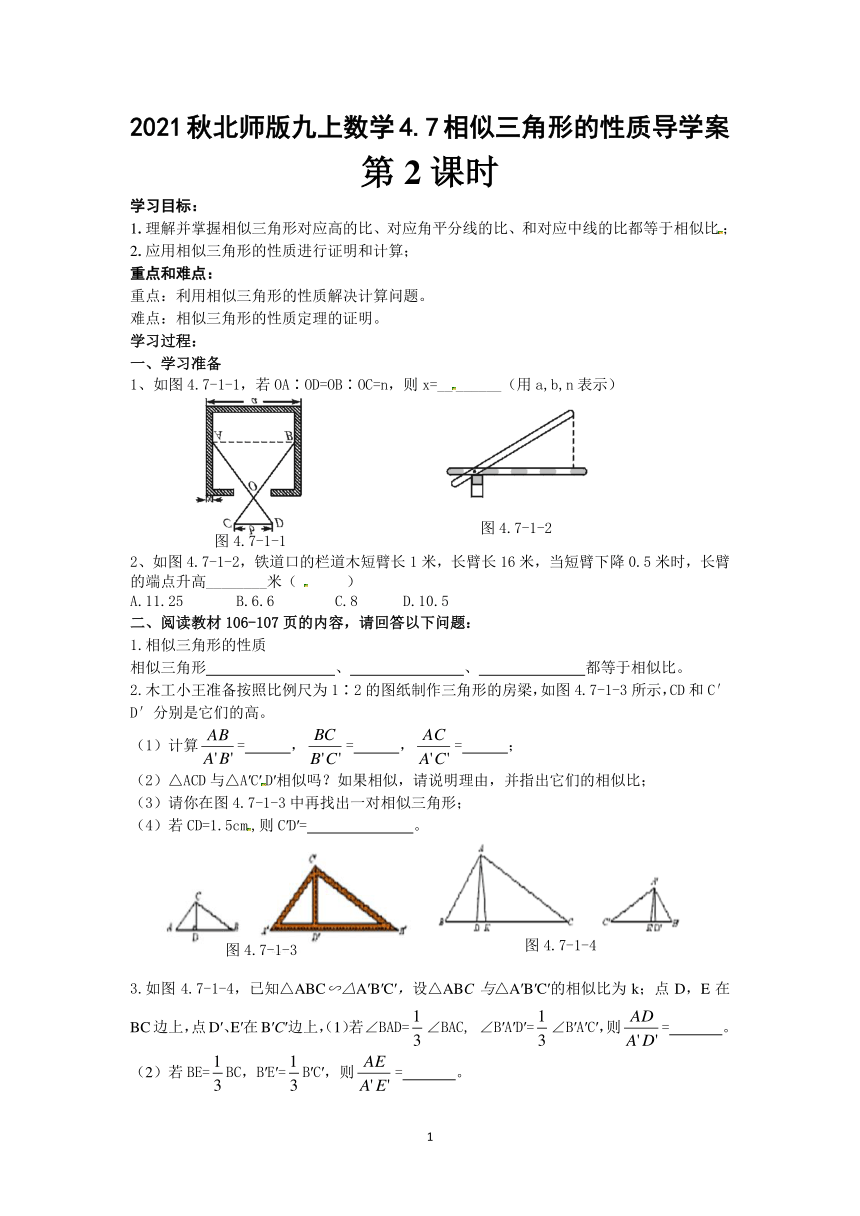
1、如图4.7-1-1,若OA∶OD=OB∶OC=n,则x=________(用a,b,n表示)
2、如图4.7-1-2,铁道口的栏道木短臂长1米,长臂长16米,当短臂下降0.5米时,长臂的端点升高________米( )
A.11.25 B.6.6 C.8 D.10.5
二、阅读教材106-107页的内容,请回答以下问题:
1.相似三角形的性质
相似三角形 、 、 都等于相似比。
2.木工小王准备按照比例尺为1∶2的图纸制作三角形的房梁,如图4.7-1-3所示,CD和C′D′分别是它们的高。
(1)计算= ,= ,= ;
(2)△ACD与△A′C′D′相似吗?如果相似,请说明理由,并指出它们的相似比;
(3)请你在图4.7-1-3中再找出一对相似三角形;
(4)若CD=1.5cm,则C′D′= 。
3.如图4.7-1-4,已知△ABC∽△A′B′C′,设△ABC与△A′B′C′的相似比为k;点D,E在BC边上,点D′、E′在B′C′边上,(1)若∠BAD=∠BAC, ∠B′A′D′=∠B′A′C′,则= 。(2)若BE=BC,B′E′=B′C′,则= 。
二、合作探究学习
1.探究1:证明本节定理(对学、群学画出图形,写出已知、求证及证明过程并展示点评)
请写出您的分析与解答:
2.探究2:请仿照课本p107页中的“例题”,解答下列问题。
如图4.7-1-5所示,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E。
(1)当SR=BC时,求DE的长;
(2)当SR=BC时,求DE的长。
请写出您的分析与解答:
三、当堂检测:
1.已知△DEF∽△ABC ,DF =5cm , AC =8cm , 则它们的相似比是 ,对应高的比是 ,对应中线的比是 ,对应角平分线的比是 。
2.如图4.7-1-6,AD是△ABC的高,点P、Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm, AD=40cm,四边形PQRS是正方形。
(1)△ARS与△ABC相似吗?为什么?
(2)求正方形PQRS的边长.
3. 如图4.7-1-7,CD是Rt△ABC的斜边AB上的高。
(1)则图中有几对相似三角形;
(2)若AD=9cm,CD=6 cm,求BD;
(3)若AB=25cm,BC=15 cm,求BD。
四、课堂小结
这节课您学到了什么知识?您还有什么疑问需要解决?
五、课后作业:
1.教材P107,随堂练习1-2题,习题4.11的1-4题
2.补充题:《天府数学》本节内容
第2课时
学习目标:
1.掌握三角形相似,则周长的比与相似比,面积的比与相似比的平方之间存在的等量关系;
2.能熟练运用三角形相似性质进行计算,并能解决一些实际问题;
重点和难点:
重点:探索相似三角形的周长比、面积比的性质。
难点:利用相似三角形的性质定理解决实际问题。
学习过程:
一、知识准备
1、已知图4.7-2-1,△ABC∽△ADE,,则△ABC的BC边上的高线与△ADE的DE边上高线的比为________;对应中线的比为________;对应角平分线的比为_________;相似比为____________。
2、如果,那么
=_________________。[
二、阅读教材109-110页的内容,请回答以下问题:
1.相似三角形的周长比与面积比的证明
如图4.7-2-2结合课本P109页相似三角形性质的证明过程,思考证明步骤的依据是什么
(1)∵△ABC∽△A′B′C′∴==== k
(2)猜想:,理由是:
∵=== k
∴ 由比例的等比性质可知=______[]
(3) ∵S△ABC=× × ,S△A B C =× × ,
∴△ABC与△A′B′C′的面积比是 。
(4)从以上证明可以发现一条规律,这个规律可归纳为:
相似三角形的周长比等于 ,面积比等于 。
2.若ΔABC∽ΔDEF的相似比是2∶3,则它们的对应高线的比是 ,对应中线的比是 ,对应角平分线的比是 ,周长比是 ,面积比是 。
二、合作探究学习
1.探究1:如图4.7-2-3,研读课本P109页中的“议一议”,探究相似多边形的周长比、面积比与相似比的关系。并对你的猜想加以证明。请写出您的分析与解答:
结论:相似四边形周长比等于 ,面积比等于 。
以此类推可得相似多边形周长比等于 ,面积比等于 。
2.探究2:请仿照课本P110页中的“例题2”,解答下列问题。
如图4.7-2-4,将 ABC沿AB方向平移得到 DEF, ABC与 DEF重叠部分(图中阴影部分)的面积是 ABC的面积的一半。已知AB=4,求 ABC平移的距离。请写出您的分析与解答:
3.探究3:拓展
如图4.7-2-5,在△ABC中,D,E分别是边AB,AC上的点,,求。请写出您的分析与解答:
三、当堂检测:
1.把一个三角形改成和它相似的三角形,如果面积扩大到原来的100倍,那么边长扩大到原来的( )A.10000倍 B.10倍 C.100倍 D.1000倍
2.在一张1:10000的地图上,一块多边形地区的面积为6 ,则这块多边形地区的实际面积为( )A.6 B.60000 C.600 D.6000
3. 如图4.7-2-5,在△ABC中,DE∥BC,且则DE= 。
4. 如图4.7-2-6,在△ABC中,∠C=90 o,D是AC上一点,DE⊥AB于E,若AB=10,BC=6,DE=2,求四边形DEBC的面积。
四、课堂小结
这节课您学到了什么知识?您还有什么疑问需要解决?
五、课后作业:
1.教材P110,随堂练习1-2题,习题4.12的1-6题
2.补充题:如右图,□ ABCD中,AE∶ED=1∶2,S△AEF=6 cm2,求S△CBF的值。
图4.7-1-2
图4.7-1-1
图4.7-1-3
图4.7-1-4
图4.7-1-5
图4.7-1-6
图4.7-1-7
图4.7-2-1
图4.7-2-2
图4.7-2-3
图4.7-2-4
图4.7-2-5
图4.7-2-6
PAGE
1
第2课时
学习目标:
1.理解并掌握相似三角形对应高的比、对应角平分线的比、和对应中线的比都等于相似比;
2.应用相似三角形的性质进行证明和计算;
重点和难点:
重点:利用相似三角形的性质解决计算问题。
难点:相似三角形的性质定理的证明。
学习过程:
一、学习准备
1、如图4.7-1-1,若OA∶OD=OB∶OC=n,则x=________(用a,b,n表示)
2、如图4.7-1-2,铁道口的栏道木短臂长1米,长臂长16米,当短臂下降0.5米时,长臂的端点升高________米( )
A.11.25 B.6.6 C.8 D.10.5
二、阅读教材106-107页的内容,请回答以下问题:
1.相似三角形的性质
相似三角形 、 、 都等于相似比。
2.木工小王准备按照比例尺为1∶2的图纸制作三角形的房梁,如图4.7-1-3所示,CD和C′D′分别是它们的高。
(1)计算= ,= ,= ;
(2)△ACD与△A′C′D′相似吗?如果相似,请说明理由,并指出它们的相似比;
(3)请你在图4.7-1-3中再找出一对相似三角形;
(4)若CD=1.5cm,则C′D′= 。
3.如图4.7-1-4,已知△ABC∽△A′B′C′,设△ABC与△A′B′C′的相似比为k;点D,E在BC边上,点D′、E′在B′C′边上,(1)若∠BAD=∠BAC, ∠B′A′D′=∠B′A′C′,则= 。(2)若BE=BC,B′E′=B′C′,则= 。
二、合作探究学习
1.探究1:证明本节定理(对学、群学画出图形,写出已知、求证及证明过程并展示点评)
请写出您的分析与解答:
2.探究2:请仿照课本p107页中的“例题”,解答下列问题。
如图4.7-1-5所示,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E。
(1)当SR=BC时,求DE的长;
(2)当SR=BC时,求DE的长。
请写出您的分析与解答:
三、当堂检测:
1.已知△DEF∽△ABC ,DF =5cm , AC =8cm , 则它们的相似比是 ,对应高的比是 ,对应中线的比是 ,对应角平分线的比是 。
2.如图4.7-1-6,AD是△ABC的高,点P、Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm, AD=40cm,四边形PQRS是正方形。
(1)△ARS与△ABC相似吗?为什么?
(2)求正方形PQRS的边长.
3. 如图4.7-1-7,CD是Rt△ABC的斜边AB上的高。
(1)则图中有几对相似三角形;
(2)若AD=9cm,CD=6 cm,求BD;
(3)若AB=25cm,BC=15 cm,求BD。
四、课堂小结
这节课您学到了什么知识?您还有什么疑问需要解决?
五、课后作业:
1.教材P107,随堂练习1-2题,习题4.11的1-4题
2.补充题:《天府数学》本节内容
第2课时
学习目标:
1.掌握三角形相似,则周长的比与相似比,面积的比与相似比的平方之间存在的等量关系;
2.能熟练运用三角形相似性质进行计算,并能解决一些实际问题;
重点和难点:
重点:探索相似三角形的周长比、面积比的性质。
难点:利用相似三角形的性质定理解决实际问题。
学习过程:
一、知识准备
1、已知图4.7-2-1,△ABC∽△ADE,,则△ABC的BC边上的高线与△ADE的DE边上高线的比为________;对应中线的比为________;对应角平分线的比为_________;相似比为____________。
2、如果,那么
=_________________。[
二、阅读教材109-110页的内容,请回答以下问题:
1.相似三角形的周长比与面积比的证明
如图4.7-2-2结合课本P109页相似三角形性质的证明过程,思考证明步骤的依据是什么
(1)∵△ABC∽△A′B′C′∴==== k
(2)猜想:,理由是:
∵=== k
∴ 由比例的等比性质可知=______[]
(3) ∵S△ABC=× × ,S△A B C =× × ,
∴△ABC与△A′B′C′的面积比是 。
(4)从以上证明可以发现一条规律,这个规律可归纳为:
相似三角形的周长比等于 ,面积比等于 。
2.若ΔABC∽ΔDEF的相似比是2∶3,则它们的对应高线的比是 ,对应中线的比是 ,对应角平分线的比是 ,周长比是 ,面积比是 。
二、合作探究学习
1.探究1:如图4.7-2-3,研读课本P109页中的“议一议”,探究相似多边形的周长比、面积比与相似比的关系。并对你的猜想加以证明。请写出您的分析与解答:
结论:相似四边形周长比等于 ,面积比等于 。
以此类推可得相似多边形周长比等于 ,面积比等于 。
2.探究2:请仿照课本P110页中的“例题2”,解答下列问题。
如图4.7-2-4,将 ABC沿AB方向平移得到 DEF, ABC与 DEF重叠部分(图中阴影部分)的面积是 ABC的面积的一半。已知AB=4,求 ABC平移的距离。请写出您的分析与解答:
3.探究3:拓展
如图4.7-2-5,在△ABC中,D,E分别是边AB,AC上的点,,求。请写出您的分析与解答:
三、当堂检测:
1.把一个三角形改成和它相似的三角形,如果面积扩大到原来的100倍,那么边长扩大到原来的( )A.10000倍 B.10倍 C.100倍 D.1000倍
2.在一张1:10000的地图上,一块多边形地区的面积为6 ,则这块多边形地区的实际面积为( )A.6 B.60000 C.600 D.6000
3. 如图4.7-2-5,在△ABC中,DE∥BC,且则DE= 。
4. 如图4.7-2-6,在△ABC中,∠C=90 o,D是AC上一点,DE⊥AB于E,若AB=10,BC=6,DE=2,求四边形DEBC的面积。
四、课堂小结
这节课您学到了什么知识?您还有什么疑问需要解决?
五、课后作业:
1.教材P110,随堂练习1-2题,习题4.12的1-6题
2.补充题:如右图,□ ABCD中,AE∶ED=1∶2,S△AEF=6 cm2,求S△CBF的值。
图4.7-1-2
图4.7-1-1
图4.7-1-3
图4.7-1-4
图4.7-1-5
图4.7-1-6
图4.7-1-7
图4.7-2-1
图4.7-2-2
图4.7-2-3
图4.7-2-4
图4.7-2-5
图4.7-2-6
PAGE
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
