苏科版八年级数学上册 3.1 勾股定理教案
文档属性
| 名称 | 苏科版八年级数学上册 3.1 勾股定理教案 |  | |
| 格式 | doc | ||
| 文件大小 | 75.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 14:18:26 | ||
图片预览

文档简介
勾股定理
【教学目标】
1.初步了解勾股定理的内容:直角三角形两直角边的平方和等于斜边的平方。
2.尝试用“割”和“补”两种方法探索教材图中以AB为边的正方形的面积,在求解的过程中判断哪一种方法更简便,总结在网格图中求图形面积的方法。
3.熟记11到20的平方,能迅速判断给定的一个平方数是几的平方,如144是12的平方。
4.对给定的已知两边长的直角三角形,能根据勾股定理求出第三边的长。
【教学重难点】
能根据勾股定理求出第三边的长。
【教学过程】
一、情景引入:
1.网格图中正方形的面积的求法。
教材的图3-1中,以AB为边的正方形的面积的常见求法有两种:
(1)用“补”的方法:将边长为AB的正方形面积看成边长为_______的正方形面积与4个两直角边长分别为_______的小直角三角形面积的差;
(2)用“割”的方法:将边长为AB的正方形面积看成边长为_______的正方形面积与4个两直角边长分别为_______的小直角三角形面积的和。
2.勾股定理
(1)直角三角形_________________________的平方和等于________________的平方。
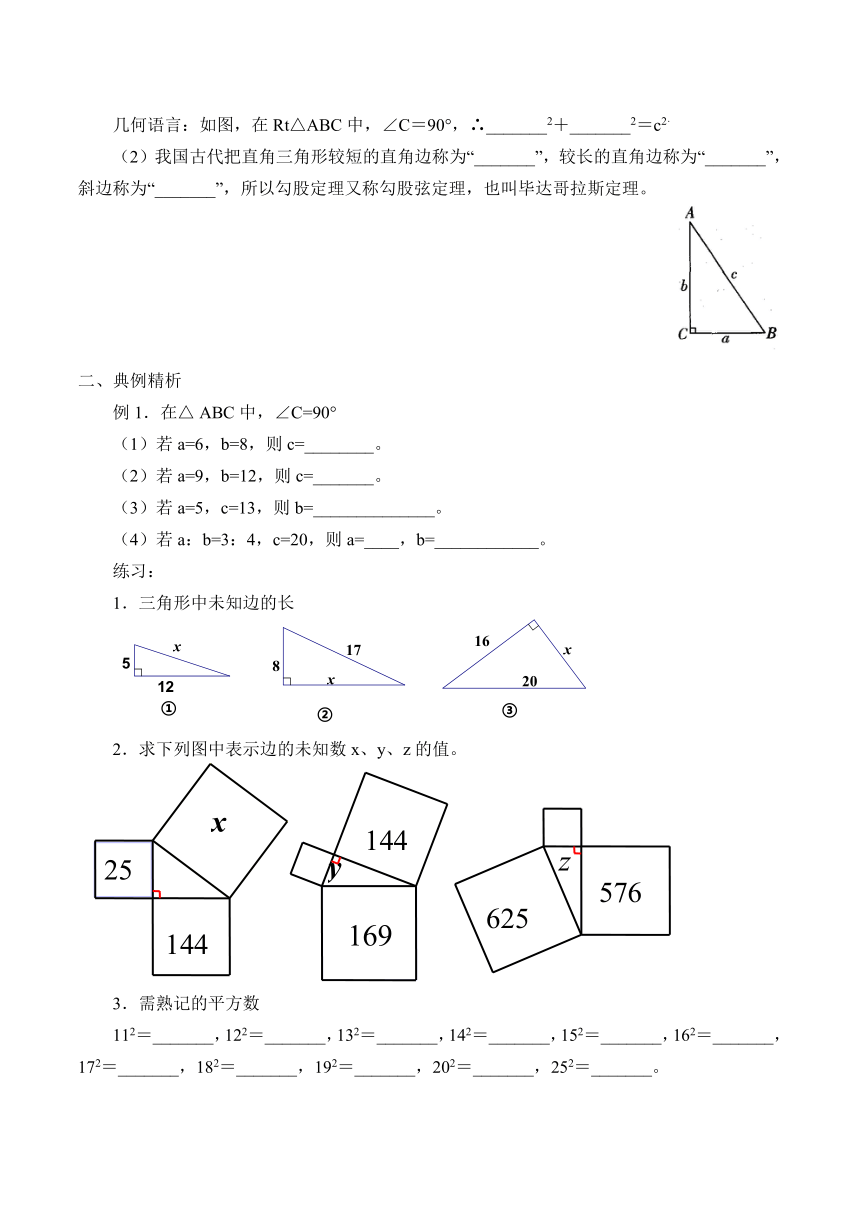
几何语言:如图,在Rt△ABC中,∠C=90°,∴_______2+_______2=c2.
(2)我国古代把直角三角形较短的直角边称为“_______”,较长的直角边称为“_______”,斜边称为“_______”,所以勾股定理又称勾股弦定理,也叫毕达哥拉斯定理。
二、典例精析
例1.在△ ABC中,∠C=90°
(1)若a=6,b=8,则c=________。
(2)若a=9,b=12,则c=_______。
(3)若a=5,c=13,则b=______________。
(4)若a:b=3:4,c=20,则a=____,b=____________。
练习:
1.三角形中未知边的长
2.求下列图中表示边的未知数x、y、z的值。
3.需熟记的平方数
112=_______,122=_______,132=_______,142=_______,152=_______,162=_______,172=_______,182=_______,192=_______,202=_______,252=_______。
例2.在Rt△ABC中,∠ACB=90°,CD是高,AC=5,BC=12,求CD的长。
例3.(1)如图①,在Rt△ABC中,∠ACB=90°,以AC.BC.AB为直径的3个半圆的面积S1.S2和S3之间有什么关系?请说明理由,若AB=4,求S1+S2的值。
变:(2)如图②,若Rt△ABC的面积为10,分别以AC.BC.AB为直径在AB的同侧作三个半圆,面积分别为S1.S2和S3,求阴影部分的面积S。
三、课堂巩固
1.直角三角形两条直角边的长分别为3,4,则斜边上的高为______。
2.如图是一棵美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形。若正方形A.B.C.D的边长分别是3,5,2,3,则最大正方形E的面积是( )
A.13 B.26 C.47 D.94
3.如图,在等腰△ABC中,AB=AC,AD是底边上的高,若AB=5cm,BC=6cm,则AD=______cm。
4.如图,在△ABC中,AC=17,BC=10,AB边上的高CD=8,则AB边的长为 ( )
A.21 B.15 C.6 D.以上答案都不对
5.斜边长为17.一条直角边长为15的直角三角形的面积为______。
6.在中,,若AB=5,则AB2+AC2+BC2=______。
四、拓展提高
如图,在△ABC中,AB=AC,P为BC上任意一点,请用学过的知识说明:AB2-AP2=PB×PC.
五、课堂小结
1.会利用割补法求网格图中几何图形的面积;
2.掌握勾股定理的用法,已知直角三角形两边求第三边;
3.简单应用勾股定理
x
y
z
576
625
144
169
144
25
A
B
P
C
【教学目标】
1.初步了解勾股定理的内容:直角三角形两直角边的平方和等于斜边的平方。
2.尝试用“割”和“补”两种方法探索教材图中以AB为边的正方形的面积,在求解的过程中判断哪一种方法更简便,总结在网格图中求图形面积的方法。
3.熟记11到20的平方,能迅速判断给定的一个平方数是几的平方,如144是12的平方。
4.对给定的已知两边长的直角三角形,能根据勾股定理求出第三边的长。
【教学重难点】
能根据勾股定理求出第三边的长。
【教学过程】
一、情景引入:
1.网格图中正方形的面积的求法。
教材的图3-1中,以AB为边的正方形的面积的常见求法有两种:
(1)用“补”的方法:将边长为AB的正方形面积看成边长为_______的正方形面积与4个两直角边长分别为_______的小直角三角形面积的差;
(2)用“割”的方法:将边长为AB的正方形面积看成边长为_______的正方形面积与4个两直角边长分别为_______的小直角三角形面积的和。
2.勾股定理
(1)直角三角形_________________________的平方和等于________________的平方。
几何语言:如图,在Rt△ABC中,∠C=90°,∴_______2+_______2=c2.
(2)我国古代把直角三角形较短的直角边称为“_______”,较长的直角边称为“_______”,斜边称为“_______”,所以勾股定理又称勾股弦定理,也叫毕达哥拉斯定理。
二、典例精析
例1.在△ ABC中,∠C=90°
(1)若a=6,b=8,则c=________。
(2)若a=9,b=12,则c=_______。
(3)若a=5,c=13,则b=______________。
(4)若a:b=3:4,c=20,则a=____,b=____________。
练习:
1.三角形中未知边的长
2.求下列图中表示边的未知数x、y、z的值。
3.需熟记的平方数
112=_______,122=_______,132=_______,142=_______,152=_______,162=_______,172=_______,182=_______,192=_______,202=_______,252=_______。
例2.在Rt△ABC中,∠ACB=90°,CD是高,AC=5,BC=12,求CD的长。
例3.(1)如图①,在Rt△ABC中,∠ACB=90°,以AC.BC.AB为直径的3个半圆的面积S1.S2和S3之间有什么关系?请说明理由,若AB=4,求S1+S2的值。
变:(2)如图②,若Rt△ABC的面积为10,分别以AC.BC.AB为直径在AB的同侧作三个半圆,面积分别为S1.S2和S3,求阴影部分的面积S。
三、课堂巩固
1.直角三角形两条直角边的长分别为3,4,则斜边上的高为______。
2.如图是一棵美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形。若正方形A.B.C.D的边长分别是3,5,2,3,则最大正方形E的面积是( )
A.13 B.26 C.47 D.94
3.如图,在等腰△ABC中,AB=AC,AD是底边上的高,若AB=5cm,BC=6cm,则AD=______cm。
4.如图,在△ABC中,AC=17,BC=10,AB边上的高CD=8,则AB边的长为 ( )
A.21 B.15 C.6 D.以上答案都不对
5.斜边长为17.一条直角边长为15的直角三角形的面积为______。
6.在中,,若AB=5,则AB2+AC2+BC2=______。
四、拓展提高
如图,在△ABC中,AB=AC,P为BC上任意一点,请用学过的知识说明:AB2-AP2=PB×PC.
五、课堂小结
1.会利用割补法求网格图中几何图形的面积;
2.掌握勾股定理的用法,已知直角三角形两边求第三边;
3.简单应用勾股定理
x
y
z
576
625
144
169
144
25
A
B
P
C
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
