2020-2021学年河北省廊坊高二(下)期末考试数学试卷人教A版(Word含答案解析)
文档属性
| 名称 | 2020-2021学年河北省廊坊高二(下)期末考试数学试卷人教A版(Word含答案解析) | 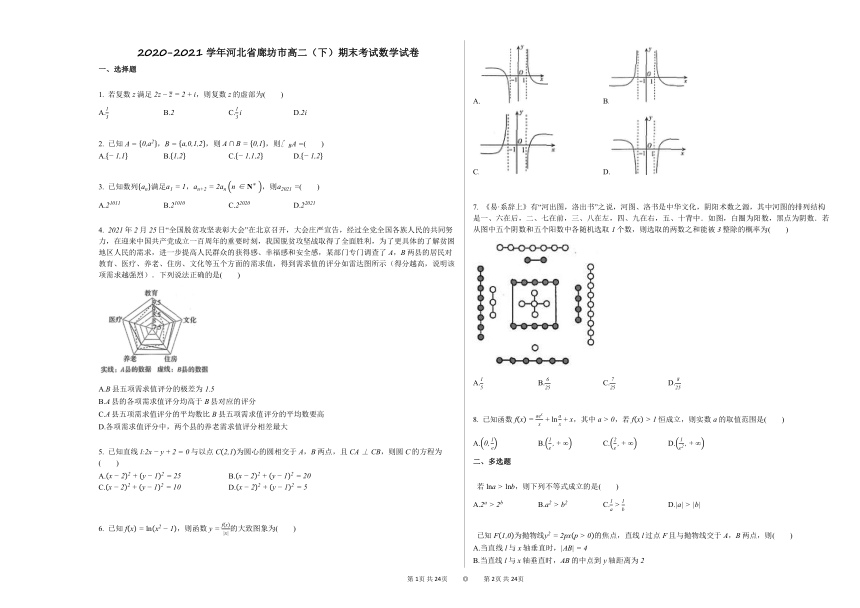 | |
| 格式 | zip | ||
| 文件大小 | 346.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 22:40:02 | ||
图片预览





文档简介
2020-2021学年河北省廊坊市高二(下)期末考试数学试卷
一、选择题
1. 若复数满足,则复数的虚部为( )
A. B. C. D.
2. 已知,,则,则( )
A. B. C. D.
3. 已知数列满足,,则( )
A. B. C. D.
4. 年月日“全国脱贫攻坚表彰大会”在北京召开,大会庄严宣告,经过全党全国各族人民的共同努力,在迎来中国共产党成立一百周年的重要时刻,我国脱贫攻坚战取得了全面胜利,为了更具体的了解贫困地区人民的需求,进一步提高人民群众的获得感、幸福感和安全感,某部门专门调查了,两县的居民对教育、医疗、养老、住房、文化等五个方面的需求值,得到需求值的评分如雷达图所示(得分越高,说明该项需求越强烈).下列说法正确的是( )
A.县五项需求值评分的极差为
B.县的各项需求值评分均高于县对应的评分
C.县五项需求值评分的平均数比县五项需求值评分的平均数要高
D.各项需求值评分中,两个县的养老需求值评分相差最大
5. 已知直线与以点为圆心的圆相交于,两点,且,则圆的方程为( )
A. B.
C. D.
6. 已知,则函数的大致图象为( )
A. B.
C. D.
7. 《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从图中五个阴数和五个阳数中各随机选取个数,则选取的两数之和能被整除的概率为( )
A. B. C. D.
8. 已知函数,其中,若恒成立,则实数的取值范围是( )
A. B. C. D.
二、多选题
若,则下列不等式成立的是( )
A. B. C. D.
已知为抛物线的焦点,直线过点且与抛物线交于,两点,则( )
A.当直线与轴垂直时,
B.当直线与轴垂直时,的中点到轴距离为
C.的最小值为
D.若点,则的最小值为
关于函数,下列说法正确的是( )
A.是偶函数 B.在区间单调递减
C.在有个零点 D.的最大值为
半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.如图的半正多面体是由棱长为的正方体“切”去个“角”后得到的几何体,它的所有顶点都在同一个正方体的棱上,则下列关于该多面体的说法中正确的是( )
A.它的表面积为
B.它的体积为
C.它的所有顶点均在同一个球面上,且该球的表面积为
D.它的任意两个共棱的面所成的锐二面角都相等
三、填空题
在的展开式中,含项的系数是,则
________;
该展开式中所有项的系数之和为________.
四、解答题
在中,内角,,所对的边分别为,,,从条件①、条件②这两个条件中选择一个作为已知条件,求:
的大小;
若,求周长的最大值.
条件①:;
条件②:.
已知数列的前项和为,满足,且对任意正整数,都有.
求数列的通项公式;
是否存在正整数,使得,,成等比数列?若存在,求出的值;若不存在,说明理由.
如图,在直三棱柱中,侧棱,,且,分别为,的中点.
证明:平面;
若,求二面角的大小.
去年,中共中央、国务院印发了《关于全面加强新时代大中小学劳动教育的意见》(以下简称《意见》),就全面贯彻党的教育方针,加强大中小学劳动教育进行了系统设计和全面部署.把劳动教育纳入人才培养全过程,促进学生形成正确的世界观、人生观、价值观.某中学为了更好的落实劳动教育课,在校园内开展了有关劳动教育的知识测评,并从参加测评的学生中随机抽取了名学生,统计了每个学生的测评得分,其统计结果如下表所示:
测评得分
频数
利用该样本的频率分布估计总体的分布,估计该校学生劳动教育的知识测评得分的均值;(注:每组数据取区间的中点值代表);
若劳动教育的知识测评得分近似地服从正态分布,其中近似为样本平均数,近似为样本的标准差,并已求得.现从全校学生中随机抽取的个学生,记测评得分在区间]之外的人数记为,求及的数学期望.(精确到)
参考数据:若随机变量,则,,,.
已知椭圆:的左顶点为,上顶点为,离心率为,为坐标原点且的面积等于.
求椭圆的标准方程;
过点作直线交椭圆于,(异于点)两点,求证:.
已知函数,.
求函数极值点的个数;
当时,证明:函数的图象恒在直线的上方.
参考答案与试题解析
2020-2021学年河北省廊坊市高二(下)期末考试数学试卷
一、选择题
1.
【答案】
A
【考点】
复数的基本概念
复数相等的充要条件
共轭复数
复数代数形式的加减运算
【解析】
此题暂无解析
【解答】
解:,
则,
所以,
即,
所以,,,
复数的虚部为.
故选.
2.
【答案】
D
【考点】
补集及其运算
集合关系中的参数取值问题
【解析】
此题暂无解析
【解答】
解:因为,且,
所以,
解得.
又,
所以,
故,
所以.
故选.
3.
【答案】
B
【考点】
等比数列的通项公式
数列递推式
【解析】
【解答】
解:由,
可得,
所以数列的奇数项是以为首项,以为公比的等比数列,
所以.
故选.
4.
【答案】
C
【考点】
众数、中位数、平均数
极差、方差与标准差
【解析】
此题暂无解析
【解答】
解:对于选项,县五项需求值评分依次为,,,,,
所以极差为,故错误;
对于选项,,两县的教育需求值评分相等,故错误;
对于选项,县五项需求值评分的平均数为,
县五项需求值评分的平均数为,故正确;
对于选项,,两县的养老需求值评分相差,
而两县的文化需求值评分相差 ,故错误.
故选.
5.
【答案】
C
【考点】
圆的标准方程
点到直线的距离公式
【解析】
此题暂无解析
【解答】
解:圆心到直线的距离,
因为,
所以是以为直角的等腰直角三角形,
所以,
即半径,
所以圆的方程为.
故选.
6.
【答案】
D
【考点】
函数的图象
【解析】
此题暂无解析
【解答】
解:构造函数.
因为,
所以函数是偶函数,图象关于轴对称,故排除,选项;
又,,故排除选项.
故选.
7.
【答案】
D
【考点】
列举法计算基本事件数及事件发生的概率
【解析】
此题暂无解析
【解答】
解:由题意可知,阴数为,,,,,阳数为,,,,.
各选一个数,共有种选法.
其和能被整除的分别为:,;,;,;,;,;,; ,;,共种选法,
∴ 选取的两数之和能被整除的概率.
故选.
8.
【答案】
B
【考点】
利用导数研究不等式恒成立问题
利用导数研究函数的单调性
利用导数研究函数的最值
【解析】
此题暂无解析
【解答】
解:由得:,
即,
∴ 在上恒成立.
∵ 在上单调递增,且,
∴ ,
∴ 在上恒成立;
∴ 在上恒成立,
构造函数,
则,
当时,,单调递增;
当时,,单调递减.
∴ ,
∴ ,
解得.
故选.
二、多选题
【答案】
A,B,D
【考点】
不等式比较两数大小
指数函数的性质
【解析】
此题暂无解析
【解答】
解:因为,
所以.
则,故正确;
,故正确;
,故不正确;
,故正确,
故选.
【答案】
A,C,D
【考点】
抛物线的求解
与抛物线有关的中点弦及弦长问题
【解析】
此题暂无解析
【解答】
解:为抛物线的焦点,
所以抛物线的方程为.
对于选项,直线与轴垂直时,不妨设,,
则,故选项正确;
对于选项,直线与轴垂直时,则,,
则的中点即为,到轴距离为,故错误;
对于选项,,不妨设在第一象限,
若直线斜率不存在,则,,即.
若直线存在斜率,设直线斜率为,
则直线的方程为,显然,
联立方程组
消去得,
设,,
则,
∴ ,
综上,故正确;
对于选项,过点向准线作垂线,垂足为,
则,
又在抛物线内部,
故当,,三点共线时,取得最小值,故正确.
故选.
【答案】
A,B
【考点】
正弦函数的单调性
函数的零点
正弦函数的奇偶性
三角函数的最值
【解析】
此题暂无解析
【解答】
解:由
,故正确;
时,,
则在上单调递减,故正确;
时,,函数有零点,,,
当时,,函数有零点,,
则在上有个零点,故错误;
因为函数为偶函数,且周期是,
所以当时,最大值为,
所以当时,最大值也为.
故函数最大值为,故错误.
故选.
【答案】
B,C,D
【考点】
球内接多面体
球的表面积和体积
柱体、锥体、台体的体积计算
棱柱的结构特征
二面角的平面角及求法
棱柱、棱锥、棱台的侧面积和表面积
【解析】
此题暂无解析
【解答】
解:如图所示,
由题意可知,该多面体的顶点为正方体各棱的中点,
故该多面体的棱为正方体相邻两条棱的中点的连线,
则该多面体有个正方形面,个等边三角形面,共个面.
对于,该多面体的棱长为,
则个正方形面的面积和为,
个等边三角形面的面积和为,
∴ 该多面体的表面积为,故错误;
对于,该多面体的体积为正方体体积减去个相同的三棱锥的体积,
即多面体体积,故正确;
对于,由对称性可知,该多面体的外接球球心为正方体的中心,
外接球的直径为正方体的面对角线长,
该球的半径为,外接球的表面积为,故正确;
设正方体底面的中心为点,
连接交该多面体的棱于点,连接,
则为的中点,且为等边三角形,
∴ .
∵ ,为的中点,
∴ ,
∵ ,分别为,的中点,则,
∴ ,
∴ 为该多面体的底面与平面所成锐二面角的平面角,
∵ 正方体的棱长为,
∴ ,
,
.
∵ 平面,平面,
∴ .
在中,,
则该多面体相邻两个面所成锐二面角的余弦值均为,故选项正确.
故选.
三、填空题
【答案】
,
【考点】
二项式系数的性质
二项展开式的特定项与特定系数
【解析】
此题暂无解析
【解答】
解:设,
令,
解得,
即,
所以,
解得,
所以二项式为,
令,则各项系数之和为.
故答案为:;
四、解答题
【答案】
解:若选择条件①:,
由正弦定理得.
因为,
所以,
因为,
所以.
因为,
所以.
若选择条件②,
由正弦定理得,
即:,
整理得.
因为,
所以,
因为,
所以.
由可知:.
在中,由余弦定理得,
即,
所以,
所以,当且仅当时等号成立,
所以,即周长的最大值为.
【考点】
正弦定理
两角和与差的正弦公式
诱导公式
余弦定理
基本不等式
【解析】
此题暂无解析
【解答】
解:若选择条件①:,
由正弦定理得.
因为,
所以,
因为,
所以.
因为,
所以.
若选择条件②,
由正弦定理得,
即:,
整理得.
因为,
所以,
因为,
所以.
由可知:.
在中,由余弦定理得,
即,
所以,
所以,当且仅当时等号成立,
所以,即周长的最大值为.
【答案】
解:由,
又对任意正整数,都成立,
即,
所以,
所以,
当时,,
即数列是以为公差,为首项的等差数列,
所以,即,
得,
又由,满足上式,
所以.
假设存在满足条件的正整数,使得,,成等比数列,
由得,,
,
若,,成等比数列,
则,
即,
因为为正整数且,
所以解得.
【考点】
数列递推式
等差数列的通项公式
等差数列的前n项和
等比数列的性质
【解析】
此题暂无解析
【解答】
解:由,
又对任意正整数,都成立,
即,
所以,
所以,
当时,,
即数列是以为公差,为首项的等差数列,
所以,即,
得,
又由,满足上式,
所以.
假设存在满足条件的正整数,使得,,成等比数列,
由得,,
,
若,,成等比数列,
则,
即,
因为为正整数且,
所以解得.
【答案】
证明:如图,取中点,分别连接,.
由题知为中点,
所以,且.
由题知为矩形,又为的中点,
所以且,
所以,且,
所以四边形为平行四边形,
所以,
又因为平面,平面,
所以平面.
解:因为三棱柱是直三棱柱,
所以平面.
如图,以为原点建立空间直角坐标系,
则,,,.
因为轴⊥平面,
所以为平面的一个法向量,
设为平面的法向量,
因为,,
所以
得
令,则,,
故可取,
则,
由二面角为锐二面角,
所以二面角的大小为.
【考点】
直线与平面平行的判定
用空间向量求平面间的夹角
【解析】
此题暂无解析
【解答】
证明:如图,取中点,分别连接,.
由题知为中点,
所以,且.
由题知为矩形,又为的中点,
所以且,
所以,且,
所以四边形为平行四边形,
所以,
又因为平面,平面,
所以平面.
解:因为三棱柱是直三棱柱,
所以平面.
如图,以为原点建立空间直角坐标系,
则,,,.
因为轴⊥平面,
所以为平面的一个法向量,
设为平面的法向量,
因为,,
所以
得
令,则,,
故可取,
则,
由二面角为锐二面角,
所以二面角的大小为.
【答案】
解:由题意知:
中间值
概率
∴ 样本平均数为
.
由可知
∴
而
,
从而测评得分在区间之外的概率为
易知,
因此
,
的数学期望为.
【考点】
用样本的频率分布估计总体分布
众数、中位数、平均数
正态分布的密度曲线
二项分布的应用
两点分布二项分布超几何分布的期望与方差
【解析】
此题暂无解析
【解答】
解:由题意知:
中间值
概率
∴ 样本平均数为
.
由可知
∴
而
,
从而测评得分在区间之外的概率为
易知,
因此
,
的数学期望为.
【答案】
解:根据题意得
解得
所以椭圆的方程为.
证明:如图,
依题意可知直线的斜率不为.
设直线的方程为:,
联立方程
化简得.
显然点在椭圆的内部,
所以,
设,,
则,,
又因为,
所以,
所以
,
所以,
所以.
【考点】
椭圆的标准方程
圆锥曲线中的定点与定值问题
【解析】
【解答】
解:根据题意得
解得
所以椭圆的方程为.
证明:如图,
依题意可知直线的斜率不为.
设直线的方程为:,
联立方程
化简得.
显然点在椭圆的内部,
所以,
设,,
则,,
又因为,
所以,
所以
,
所以,
所以.
【答案】
解:,
则.
设,则.
令,
又,得.
当时,;
当时,,
所以在内单调递增,在内单调递减.
又,,,
因此,当时,有唯一解,设为,
从而时,,即,单调递增;
时,,即,单调递减,
故在区间内有唯一极大值点,没有极小值点,
即函数的极值点个数为.
证明:要证明函数的图象恒在直线的上方.
即证恒成立,
即恒成立.
令,
因为,
设,
则.
令,由得,
当时,,
当时,,
所以在内单调递增,在内单调递减.
由得,,,.
当,
即时,.
此时函数在内单调递增,.
当,
即时,
因为,
所以,在内恒成立,而
在区间内有且只有一个零点,记为,
则函数在内单调递增,在内单调递减.
又因为,,
所以此时.
由可知,当时,对任意总有,
即时,函数的图象恒在直线的上方.
【考点】
利用导数研究函数的极值
利用导数研究不等式恒成立问题
【解析】
【解答】
解:,
则.
设,则.
令,
又,得.
当时,;
当时,,
所以在内单调递增,在内单调递减.
又,,,
因此,当时,有唯一解,设为,
从而时,,即,单调递增;
时,,即,单调递减,
故在区间内有唯一极大值点,没有极小值点,
即函数的极值点个数为.
证明:要证明函数的图象恒在直线的上方.
即证恒成立,
即恒成立.
令,
因为,
设,
则.
令,由得,
当时,,
当时,,
所以在内单调递增,在内单调递减.
由得,,,.
当,
即时,.
此时函数在内单调递增,.
当,
即时,
因为,
所以,在内恒成立,而
在区间内有且只有一个零点,记为,
则函数在内单调递增,在内单调递减.
又因为,,
所以此时.
由可知,当时,对任意总有,
即时,函数的图象恒在直线的上方.
第3页 共16页 ◎ 第4页 共16页
第1页 共16页 ◎ 第2页 共16页
一、选择题
1. 若复数满足,则复数的虚部为( )
A. B. C. D.
2. 已知,,则,则( )
A. B. C. D.
3. 已知数列满足,,则( )
A. B. C. D.
4. 年月日“全国脱贫攻坚表彰大会”在北京召开,大会庄严宣告,经过全党全国各族人民的共同努力,在迎来中国共产党成立一百周年的重要时刻,我国脱贫攻坚战取得了全面胜利,为了更具体的了解贫困地区人民的需求,进一步提高人民群众的获得感、幸福感和安全感,某部门专门调查了,两县的居民对教育、医疗、养老、住房、文化等五个方面的需求值,得到需求值的评分如雷达图所示(得分越高,说明该项需求越强烈).下列说法正确的是( )
A.县五项需求值评分的极差为
B.县的各项需求值评分均高于县对应的评分
C.县五项需求值评分的平均数比县五项需求值评分的平均数要高
D.各项需求值评分中,两个县的养老需求值评分相差最大
5. 已知直线与以点为圆心的圆相交于,两点,且,则圆的方程为( )
A. B.
C. D.
6. 已知,则函数的大致图象为( )
A. B.
C. D.
7. 《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从图中五个阴数和五个阳数中各随机选取个数,则选取的两数之和能被整除的概率为( )
A. B. C. D.
8. 已知函数,其中,若恒成立,则实数的取值范围是( )
A. B. C. D.
二、多选题
若,则下列不等式成立的是( )
A. B. C. D.
已知为抛物线的焦点,直线过点且与抛物线交于,两点,则( )
A.当直线与轴垂直时,
B.当直线与轴垂直时,的中点到轴距离为
C.的最小值为
D.若点,则的最小值为
关于函数,下列说法正确的是( )
A.是偶函数 B.在区间单调递减
C.在有个零点 D.的最大值为
半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体,体现了数学的对称美.如图的半正多面体是由棱长为的正方体“切”去个“角”后得到的几何体,它的所有顶点都在同一个正方体的棱上,则下列关于该多面体的说法中正确的是( )
A.它的表面积为
B.它的体积为
C.它的所有顶点均在同一个球面上,且该球的表面积为
D.它的任意两个共棱的面所成的锐二面角都相等
三、填空题
在的展开式中,含项的系数是,则
________;
该展开式中所有项的系数之和为________.
四、解答题
在中,内角,,所对的边分别为,,,从条件①、条件②这两个条件中选择一个作为已知条件,求:
的大小;
若,求周长的最大值.
条件①:;
条件②:.
已知数列的前项和为,满足,且对任意正整数,都有.
求数列的通项公式;
是否存在正整数,使得,,成等比数列?若存在,求出的值;若不存在,说明理由.
如图,在直三棱柱中,侧棱,,且,分别为,的中点.
证明:平面;
若,求二面角的大小.
去年,中共中央、国务院印发了《关于全面加强新时代大中小学劳动教育的意见》(以下简称《意见》),就全面贯彻党的教育方针,加强大中小学劳动教育进行了系统设计和全面部署.把劳动教育纳入人才培养全过程,促进学生形成正确的世界观、人生观、价值观.某中学为了更好的落实劳动教育课,在校园内开展了有关劳动教育的知识测评,并从参加测评的学生中随机抽取了名学生,统计了每个学生的测评得分,其统计结果如下表所示:
测评得分
频数
利用该样本的频率分布估计总体的分布,估计该校学生劳动教育的知识测评得分的均值;(注:每组数据取区间的中点值代表);
若劳动教育的知识测评得分近似地服从正态分布,其中近似为样本平均数,近似为样本的标准差,并已求得.现从全校学生中随机抽取的个学生,记测评得分在区间]之外的人数记为,求及的数学期望.(精确到)
参考数据:若随机变量,则,,,.
已知椭圆:的左顶点为,上顶点为,离心率为,为坐标原点且的面积等于.
求椭圆的标准方程;
过点作直线交椭圆于,(异于点)两点,求证:.
已知函数,.
求函数极值点的个数;
当时,证明:函数的图象恒在直线的上方.
参考答案与试题解析
2020-2021学年河北省廊坊市高二(下)期末考试数学试卷
一、选择题
1.
【答案】
A
【考点】
复数的基本概念
复数相等的充要条件
共轭复数
复数代数形式的加减运算
【解析】
此题暂无解析
【解答】
解:,
则,
所以,
即,
所以,,,
复数的虚部为.
故选.
2.
【答案】
D
【考点】
补集及其运算
集合关系中的参数取值问题
【解析】
此题暂无解析
【解答】
解:因为,且,
所以,
解得.
又,
所以,
故,
所以.
故选.
3.
【答案】
B
【考点】
等比数列的通项公式
数列递推式
【解析】
【解答】
解:由,
可得,
所以数列的奇数项是以为首项,以为公比的等比数列,
所以.
故选.
4.
【答案】
C
【考点】
众数、中位数、平均数
极差、方差与标准差
【解析】
此题暂无解析
【解答】
解:对于选项,县五项需求值评分依次为,,,,,
所以极差为,故错误;
对于选项,,两县的教育需求值评分相等,故错误;
对于选项,县五项需求值评分的平均数为,
县五项需求值评分的平均数为,故正确;
对于选项,,两县的养老需求值评分相差,
而两县的文化需求值评分相差 ,故错误.
故选.
5.
【答案】
C
【考点】
圆的标准方程
点到直线的距离公式
【解析】
此题暂无解析
【解答】
解:圆心到直线的距离,
因为,
所以是以为直角的等腰直角三角形,
所以,
即半径,
所以圆的方程为.
故选.
6.
【答案】
D
【考点】
函数的图象
【解析】
此题暂无解析
【解答】
解:构造函数.
因为,
所以函数是偶函数,图象关于轴对称,故排除,选项;
又,,故排除选项.
故选.
7.
【答案】
D
【考点】
列举法计算基本事件数及事件发生的概率
【解析】
此题暂无解析
【解答】
解:由题意可知,阴数为,,,,,阳数为,,,,.
各选一个数,共有种选法.
其和能被整除的分别为:,;,;,;,;,;,; ,;,共种选法,
∴ 选取的两数之和能被整除的概率.
故选.
8.
【答案】
B
【考点】
利用导数研究不等式恒成立问题
利用导数研究函数的单调性
利用导数研究函数的最值
【解析】
此题暂无解析
【解答】
解:由得:,
即,
∴ 在上恒成立.
∵ 在上单调递增,且,
∴ ,
∴ 在上恒成立;
∴ 在上恒成立,
构造函数,
则,
当时,,单调递增;
当时,,单调递减.
∴ ,
∴ ,
解得.
故选.
二、多选题
【答案】
A,B,D
【考点】
不等式比较两数大小
指数函数的性质
【解析】
此题暂无解析
【解答】
解:因为,
所以.
则,故正确;
,故正确;
,故不正确;
,故正确,
故选.
【答案】
A,C,D
【考点】
抛物线的求解
与抛物线有关的中点弦及弦长问题
【解析】
此题暂无解析
【解答】
解:为抛物线的焦点,
所以抛物线的方程为.
对于选项,直线与轴垂直时,不妨设,,
则,故选项正确;
对于选项,直线与轴垂直时,则,,
则的中点即为,到轴距离为,故错误;
对于选项,,不妨设在第一象限,
若直线斜率不存在,则,,即.
若直线存在斜率,设直线斜率为,
则直线的方程为,显然,
联立方程组
消去得,
设,,
则,
∴ ,
综上,故正确;
对于选项,过点向准线作垂线,垂足为,
则,
又在抛物线内部,
故当,,三点共线时,取得最小值,故正确.
故选.
【答案】
A,B
【考点】
正弦函数的单调性
函数的零点
正弦函数的奇偶性
三角函数的最值
【解析】
此题暂无解析
【解答】
解:由
,故正确;
时,,
则在上单调递减,故正确;
时,,函数有零点,,,
当时,,函数有零点,,
则在上有个零点,故错误;
因为函数为偶函数,且周期是,
所以当时,最大值为,
所以当时,最大值也为.
故函数最大值为,故错误.
故选.
【答案】
B,C,D
【考点】
球内接多面体
球的表面积和体积
柱体、锥体、台体的体积计算
棱柱的结构特征
二面角的平面角及求法
棱柱、棱锥、棱台的侧面积和表面积
【解析】
此题暂无解析
【解答】
解:如图所示,
由题意可知,该多面体的顶点为正方体各棱的中点,
故该多面体的棱为正方体相邻两条棱的中点的连线,
则该多面体有个正方形面,个等边三角形面,共个面.
对于,该多面体的棱长为,
则个正方形面的面积和为,
个等边三角形面的面积和为,
∴ 该多面体的表面积为,故错误;
对于,该多面体的体积为正方体体积减去个相同的三棱锥的体积,
即多面体体积,故正确;
对于,由对称性可知,该多面体的外接球球心为正方体的中心,
外接球的直径为正方体的面对角线长,
该球的半径为,外接球的表面积为,故正确;
设正方体底面的中心为点,
连接交该多面体的棱于点,连接,
则为的中点,且为等边三角形,
∴ .
∵ ,为的中点,
∴ ,
∵ ,分别为,的中点,则,
∴ ,
∴ 为该多面体的底面与平面所成锐二面角的平面角,
∵ 正方体的棱长为,
∴ ,
,
.
∵ 平面,平面,
∴ .
在中,,
则该多面体相邻两个面所成锐二面角的余弦值均为,故选项正确.
故选.
三、填空题
【答案】
,
【考点】
二项式系数的性质
二项展开式的特定项与特定系数
【解析】
此题暂无解析
【解答】
解:设,
令,
解得,
即,
所以,
解得,
所以二项式为,
令,则各项系数之和为.
故答案为:;
四、解答题
【答案】
解:若选择条件①:,
由正弦定理得.
因为,
所以,
因为,
所以.
因为,
所以.
若选择条件②,
由正弦定理得,
即:,
整理得.
因为,
所以,
因为,
所以.
由可知:.
在中,由余弦定理得,
即,
所以,
所以,当且仅当时等号成立,
所以,即周长的最大值为.
【考点】
正弦定理
两角和与差的正弦公式
诱导公式
余弦定理
基本不等式
【解析】
此题暂无解析
【解答】
解:若选择条件①:,
由正弦定理得.
因为,
所以,
因为,
所以.
因为,
所以.
若选择条件②,
由正弦定理得,
即:,
整理得.
因为,
所以,
因为,
所以.
由可知:.
在中,由余弦定理得,
即,
所以,
所以,当且仅当时等号成立,
所以,即周长的最大值为.
【答案】
解:由,
又对任意正整数,都成立,
即,
所以,
所以,
当时,,
即数列是以为公差,为首项的等差数列,
所以,即,
得,
又由,满足上式,
所以.
假设存在满足条件的正整数,使得,,成等比数列,
由得,,
,
若,,成等比数列,
则,
即,
因为为正整数且,
所以解得.
【考点】
数列递推式
等差数列的通项公式
等差数列的前n项和
等比数列的性质
【解析】
此题暂无解析
【解答】
解:由,
又对任意正整数,都成立,
即,
所以,
所以,
当时,,
即数列是以为公差,为首项的等差数列,
所以,即,
得,
又由,满足上式,
所以.
假设存在满足条件的正整数,使得,,成等比数列,
由得,,
,
若,,成等比数列,
则,
即,
因为为正整数且,
所以解得.
【答案】
证明:如图,取中点,分别连接,.
由题知为中点,
所以,且.
由题知为矩形,又为的中点,
所以且,
所以,且,
所以四边形为平行四边形,
所以,
又因为平面,平面,
所以平面.
解:因为三棱柱是直三棱柱,
所以平面.
如图,以为原点建立空间直角坐标系,
则,,,.
因为轴⊥平面,
所以为平面的一个法向量,
设为平面的法向量,
因为,,
所以
得
令,则,,
故可取,
则,
由二面角为锐二面角,
所以二面角的大小为.
【考点】
直线与平面平行的判定
用空间向量求平面间的夹角
【解析】
此题暂无解析
【解答】
证明:如图,取中点,分别连接,.
由题知为中点,
所以,且.
由题知为矩形,又为的中点,
所以且,
所以,且,
所以四边形为平行四边形,
所以,
又因为平面,平面,
所以平面.
解:因为三棱柱是直三棱柱,
所以平面.
如图,以为原点建立空间直角坐标系,
则,,,.
因为轴⊥平面,
所以为平面的一个法向量,
设为平面的法向量,
因为,,
所以
得
令,则,,
故可取,
则,
由二面角为锐二面角,
所以二面角的大小为.
【答案】
解:由题意知:
中间值
概率
∴ 样本平均数为
.
由可知
∴
而
,
从而测评得分在区间之外的概率为
易知,
因此
,
的数学期望为.
【考点】
用样本的频率分布估计总体分布
众数、中位数、平均数
正态分布的密度曲线
二项分布的应用
两点分布二项分布超几何分布的期望与方差
【解析】
此题暂无解析
【解答】
解:由题意知:
中间值
概率
∴ 样本平均数为
.
由可知
∴
而
,
从而测评得分在区间之外的概率为
易知,
因此
,
的数学期望为.
【答案】
解:根据题意得
解得
所以椭圆的方程为.
证明:如图,
依题意可知直线的斜率不为.
设直线的方程为:,
联立方程
化简得.
显然点在椭圆的内部,
所以,
设,,
则,,
又因为,
所以,
所以
,
所以,
所以.
【考点】
椭圆的标准方程
圆锥曲线中的定点与定值问题
【解析】
【解答】
解:根据题意得
解得
所以椭圆的方程为.
证明:如图,
依题意可知直线的斜率不为.
设直线的方程为:,
联立方程
化简得.
显然点在椭圆的内部,
所以,
设,,
则,,
又因为,
所以,
所以
,
所以,
所以.
【答案】
解:,
则.
设,则.
令,
又,得.
当时,;
当时,,
所以在内单调递增,在内单调递减.
又,,,
因此,当时,有唯一解,设为,
从而时,,即,单调递增;
时,,即,单调递减,
故在区间内有唯一极大值点,没有极小值点,
即函数的极值点个数为.
证明:要证明函数的图象恒在直线的上方.
即证恒成立,
即恒成立.
令,
因为,
设,
则.
令,由得,
当时,,
当时,,
所以在内单调递增,在内单调递减.
由得,,,.
当,
即时,.
此时函数在内单调递增,.
当,
即时,
因为,
所以,在内恒成立,而
在区间内有且只有一个零点,记为,
则函数在内单调递增,在内单调递减.
又因为,,
所以此时.
由可知,当时,对任意总有,
即时,函数的图象恒在直线的上方.
【考点】
利用导数研究函数的极值
利用导数研究不等式恒成立问题
【解析】
【解答】
解:,
则.
设,则.
令,
又,得.
当时,;
当时,,
所以在内单调递增,在内单调递减.
又,,,
因此,当时,有唯一解,设为,
从而时,,即,单调递增;
时,,即,单调递减,
故在区间内有唯一极大值点,没有极小值点,
即函数的极值点个数为.
证明:要证明函数的图象恒在直线的上方.
即证恒成立,
即恒成立.
令,
因为,
设,
则.
令,由得,
当时,,
当时,,
所以在内单调递增,在内单调递减.
由得,,,.
当,
即时,.
此时函数在内单调递增,.
当,
即时,
因为,
所以,在内恒成立,而
在区间内有且只有一个零点,记为,
则函数在内单调递增,在内单调递减.
又因为,,
所以此时.
由可知,当时,对任意总有,
即时,函数的图象恒在直线的上方.
第3页 共16页 ◎ 第4页 共16页
第1页 共16页 ◎ 第2页 共16页
同课章节目录
