黑龙江省肇州县第三中学2020-2021学年九年级上学期期中考试数学试卷(word版无答案)
文档属性
| 名称 | 黑龙江省肇州县第三中学2020-2021学年九年级上学期期中考试数学试卷(word版无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 373.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 19:25:16 | ||
图片预览
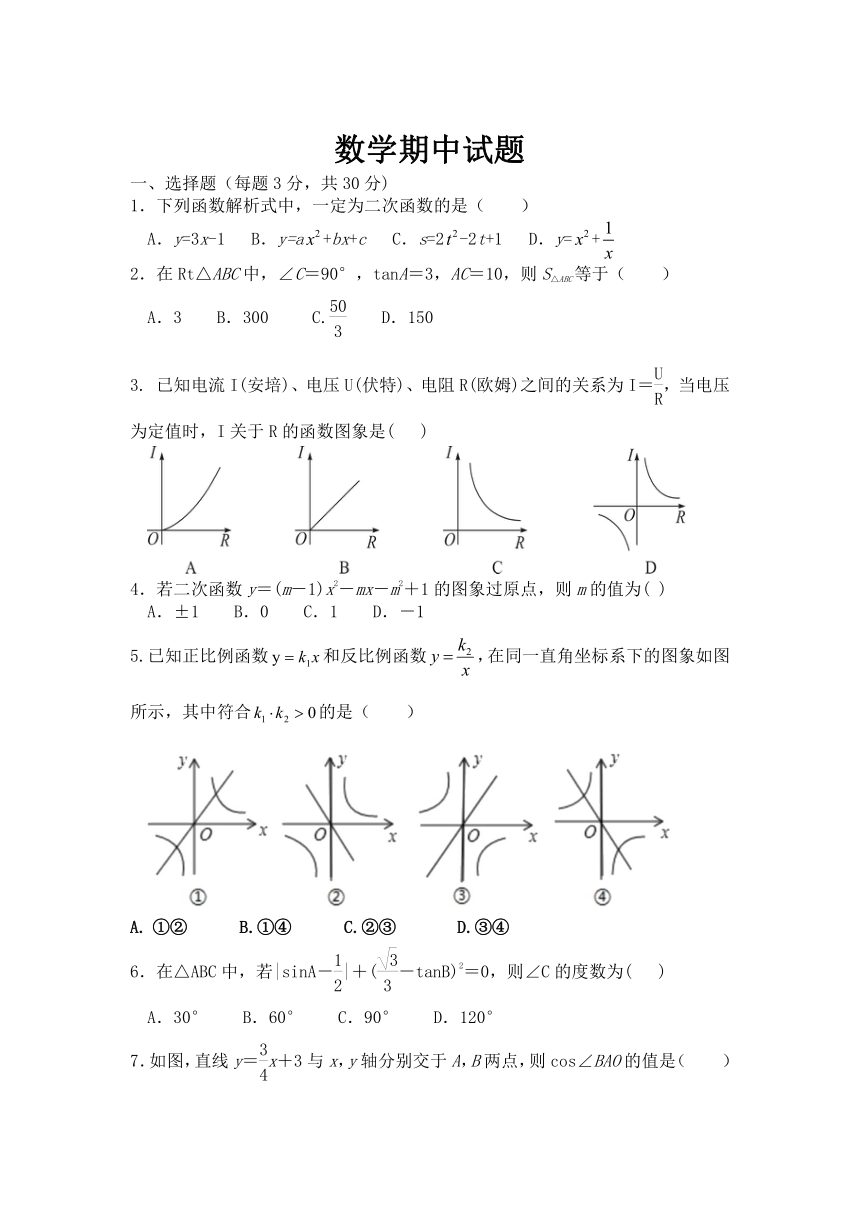

文档简介
数学期中试题
一、选择题(每题3分,共30分)
1.下列函数解析式中,一定为二次函数的是( )
A.y=3x-1 B.y=a+bx+c C.s=2-2t+1 D.y=+
2.在Rt△ABC中,∠C=90°,tanA=3,AC=10,则S△ABC等于( )
A.3 B.300 C. D.150
3. 已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为I=,当电压为定值时,I关于R的函数图象是( )
4.若二次函数y=(m-1)x2-mx-m2+1的图象过原点,则m的值为( )
A.±1 B.0 C.1 D.-1
5.已知正比例函数和反比例函数,在同一直角坐标系下的图象如图所示,其中符合的是( )
A. ①② B.①④ C.②③ D.③④
6.在△ABC中,若|sinA-|+(-tanB)2=0,则∠C的度数为( )
A.30° B.60° C.90° D.120°
7.如图,直线y=x+3与x,y轴分别交于A,B两点,则cos∠BAO的值是( )
A. B. C. D.
(7) (8) (10)
8. 一次函数y1=kx+b和反比例函数y2=的图象如图,则使y1>y2的x范围是( )
A.x<-2或x>3 B.-2<x<0或x>3
C.x<-2或0<x<3 D.-2<x<3
9.若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45° B.45°<α<60°
C.60°<α<90° D.30°<α<60°
10.如图,点A在双曲线上,点B在双曲线y= (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D,连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
A.2 B.4 C.6 D.9
二、填空题(每题3分,共30分)
11.抛物线y=2(x-3)2+1的顶点坐标是__________.
12.若点P(4,6)、点Q(-3,b)都是反比例函数y= (k≠0)图象上的点,则b=________.
13.一斜坡的坡度为1∶3,如果某人站的位置的水平宽度为9米,则他所在的位置的铅直高度为__________.
14.已知函数的图象是开口向上的抛物线,则m的值为______.
15.如果两个相似三角形的面积的比是9:16,那么它们的周长的比是___________
16.在反比例函数的图象的每一象限内,y随x的增大而减小,则m的取值范围是___________
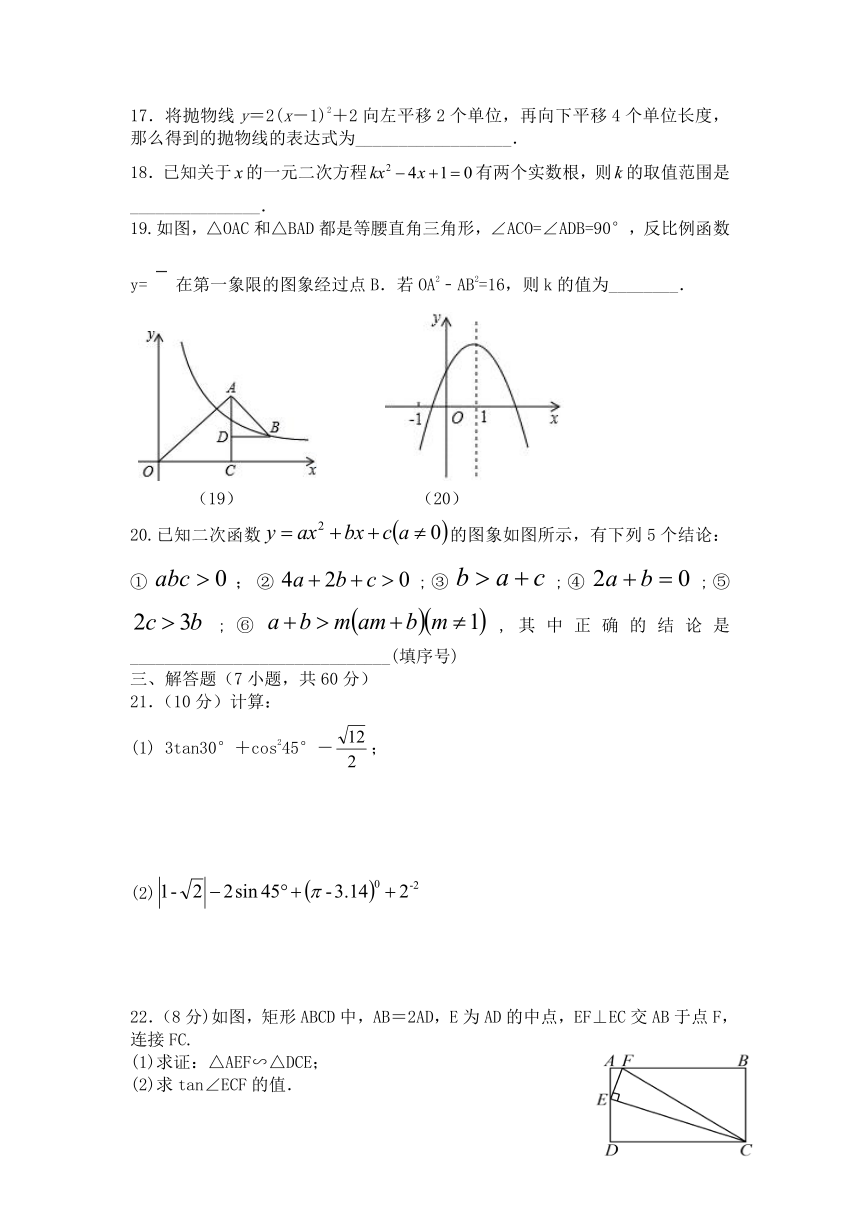
17.将抛物线y=2(x-1)2+2向左平移2个单位,再向下平移4个单位长度,那么得到的抛物线的表达式为__________________.
18.已知关于的一元二次方程有两个实数根,则的取值范围是_______________.
19.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= 在第一象限的图象经过点B.若OA2﹣AB2=16,则k的值为________.
(19) (20)
20.已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤;⑥,其中正确的结论是______________________________(填序号)
三、解答题(7小题,共60分)
21.(10分)计算:
(1) 3tan30°+cos245°-;
(2)
22.(8分)如图,矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
(1)求证:△AEF∽△DCE;
(2)求tan∠ECF的值.
23.(8分)将抛物线y=x2﹣4x+4沿y轴向下平移9个单位,所得新抛物线与x轴正半轴交于点B,与y轴交于点C,顶点为D.求:
(1)点B、C、D坐标;
(2)△BCD的面积.
24.(8分)为了预防流感,某校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,生才能进入教室?
25.(8分)如图,AB、CD为两个建筑物,两建筑物底部之间的水平地面上有一点M . 从建筑物AB的顶点A测得M点俯角为45°,从建筑物CD的顶点C测得M点的俯角为75°,测得建筑物AB的顶点A的俯角为30°. 若已知建筑物AB的高度为20米,求两建筑物顶点A、C之间的距离(结果精确到1m,参考数据:)
26.(8分)如图,直线y=2x+2与y轴交于A点,与反比例函数y=(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数y=(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
27.(10分)如图,直线y=k1x(x≥0)与双曲线y=(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C.
(1)求k1与k2的值;
(2)求直线PC的表达式;
(3)直接写出线段AB扫过的面积.
一、选择题(每题3分,共30分)
1.下列函数解析式中,一定为二次函数的是( )
A.y=3x-1 B.y=a+bx+c C.s=2-2t+1 D.y=+
2.在Rt△ABC中,∠C=90°,tanA=3,AC=10,则S△ABC等于( )
A.3 B.300 C. D.150
3. 已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为I=,当电压为定值时,I关于R的函数图象是( )
4.若二次函数y=(m-1)x2-mx-m2+1的图象过原点,则m的值为( )
A.±1 B.0 C.1 D.-1
5.已知正比例函数和反比例函数,在同一直角坐标系下的图象如图所示,其中符合的是( )
A. ①② B.①④ C.②③ D.③④
6.在△ABC中,若|sinA-|+(-tanB)2=0,则∠C的度数为( )
A.30° B.60° C.90° D.120°
7.如图,直线y=x+3与x,y轴分别交于A,B两点,则cos∠BAO的值是( )
A. B. C. D.
(7) (8) (10)
8. 一次函数y1=kx+b和反比例函数y2=的图象如图,则使y1>y2的x范围是( )
A.x<-2或x>3 B.-2<x<0或x>3
C.x<-2或0<x<3 D.-2<x<3
9.若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45° B.45°<α<60°
C.60°<α<90° D.30°<α<60°
10.如图,点A在双曲线上,点B在双曲线y= (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D,连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
A.2 B.4 C.6 D.9
二、填空题(每题3分,共30分)
11.抛物线y=2(x-3)2+1的顶点坐标是__________.
12.若点P(4,6)、点Q(-3,b)都是反比例函数y= (k≠0)图象上的点,则b=________.
13.一斜坡的坡度为1∶3,如果某人站的位置的水平宽度为9米,则他所在的位置的铅直高度为__________.
14.已知函数的图象是开口向上的抛物线,则m的值为______.
15.如果两个相似三角形的面积的比是9:16,那么它们的周长的比是___________
16.在反比例函数的图象的每一象限内,y随x的增大而减小,则m的取值范围是___________
17.将抛物线y=2(x-1)2+2向左平移2个单位,再向下平移4个单位长度,那么得到的抛物线的表达式为__________________.
18.已知关于的一元二次方程有两个实数根,则的取值范围是_______________.
19.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= 在第一象限的图象经过点B.若OA2﹣AB2=16,则k的值为________.
(19) (20)
20.已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤;⑥,其中正确的结论是______________________________(填序号)
三、解答题(7小题,共60分)
21.(10分)计算:
(1) 3tan30°+cos245°-;
(2)
22.(8分)如图,矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
(1)求证:△AEF∽△DCE;
(2)求tan∠ECF的值.
23.(8分)将抛物线y=x2﹣4x+4沿y轴向下平移9个单位,所得新抛物线与x轴正半轴交于点B,与y轴交于点C,顶点为D.求:
(1)点B、C、D坐标;
(2)△BCD的面积.
24.(8分)为了预防流感,某校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,生才能进入教室?
25.(8分)如图,AB、CD为两个建筑物,两建筑物底部之间的水平地面上有一点M . 从建筑物AB的顶点A测得M点俯角为45°,从建筑物CD的顶点C测得M点的俯角为75°,测得建筑物AB的顶点A的俯角为30°. 若已知建筑物AB的高度为20米,求两建筑物顶点A、C之间的距离(结果精确到1m,参考数据:)
26.(8分)如图,直线y=2x+2与y轴交于A点,与反比例函数y=(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数y=(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
27.(10分)如图,直线y=k1x(x≥0)与双曲线y=(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C.
(1)求k1与k2的值;
(2)求直线PC的表达式;
(3)直接写出线段AB扫过的面积.
同课章节目录
