山东省济宁市曲阜第一中学2021-2022学年高二上学期10月月考数学试题(PDF版含答案)
文档属性
| 名称 | 山东省济宁市曲阜第一中学2021-2022学年高二上学期10月月考数学试题(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 303.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 19:30:32 | ||
图片预览



文档简介
曲阜一中高二数学 10 月份月考
数学试卷
一、选择题(本题共 8 道小题,每小题 5 分,共 40 分)
1.经过点(1,0),且斜率为 2的直线的方程是( )
A. 2x y 2 0 B. 2x y 2 0 C. x 2y 1 0 D. x 2y 1 0
2.两平行直线 kx 6y 2 0与 4x 3y 4 0之间的距离为 ( )
1 2 6
A. B. C. 1 D.
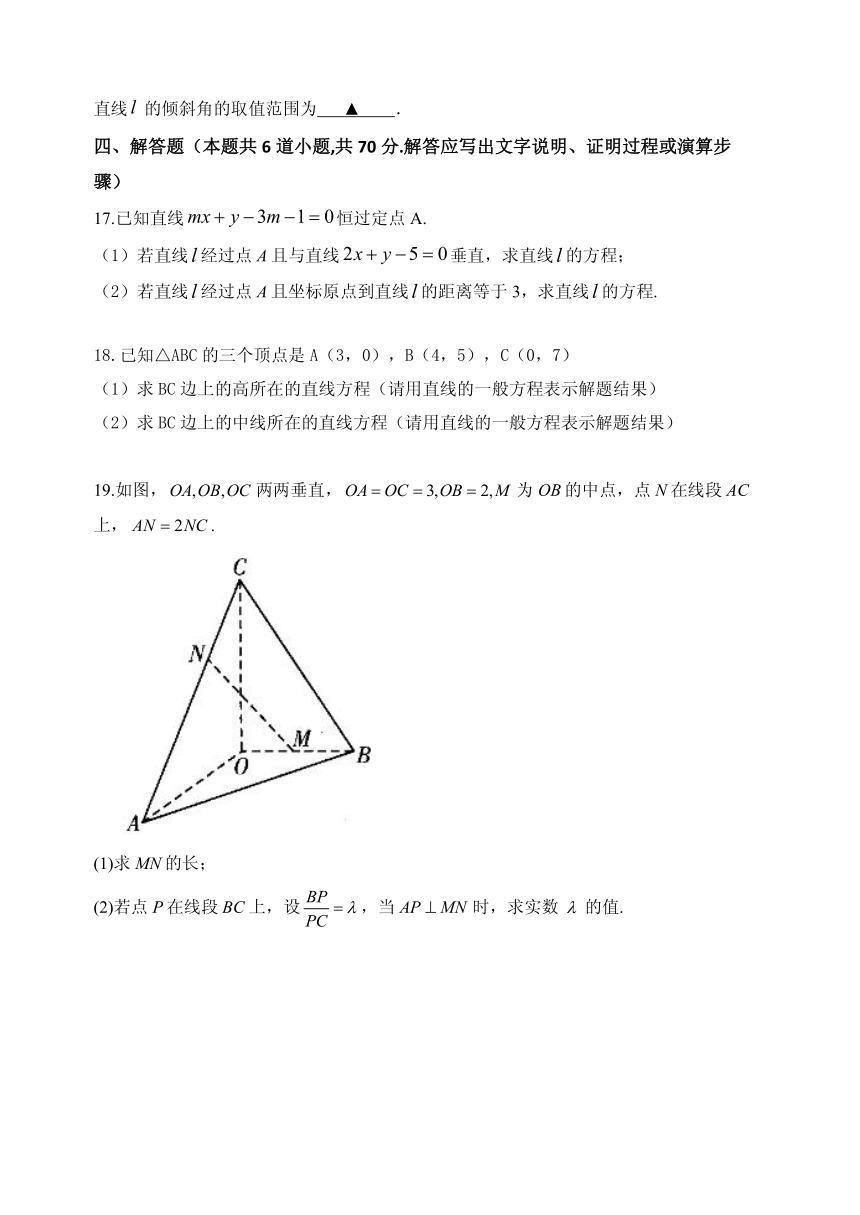
5 5 5
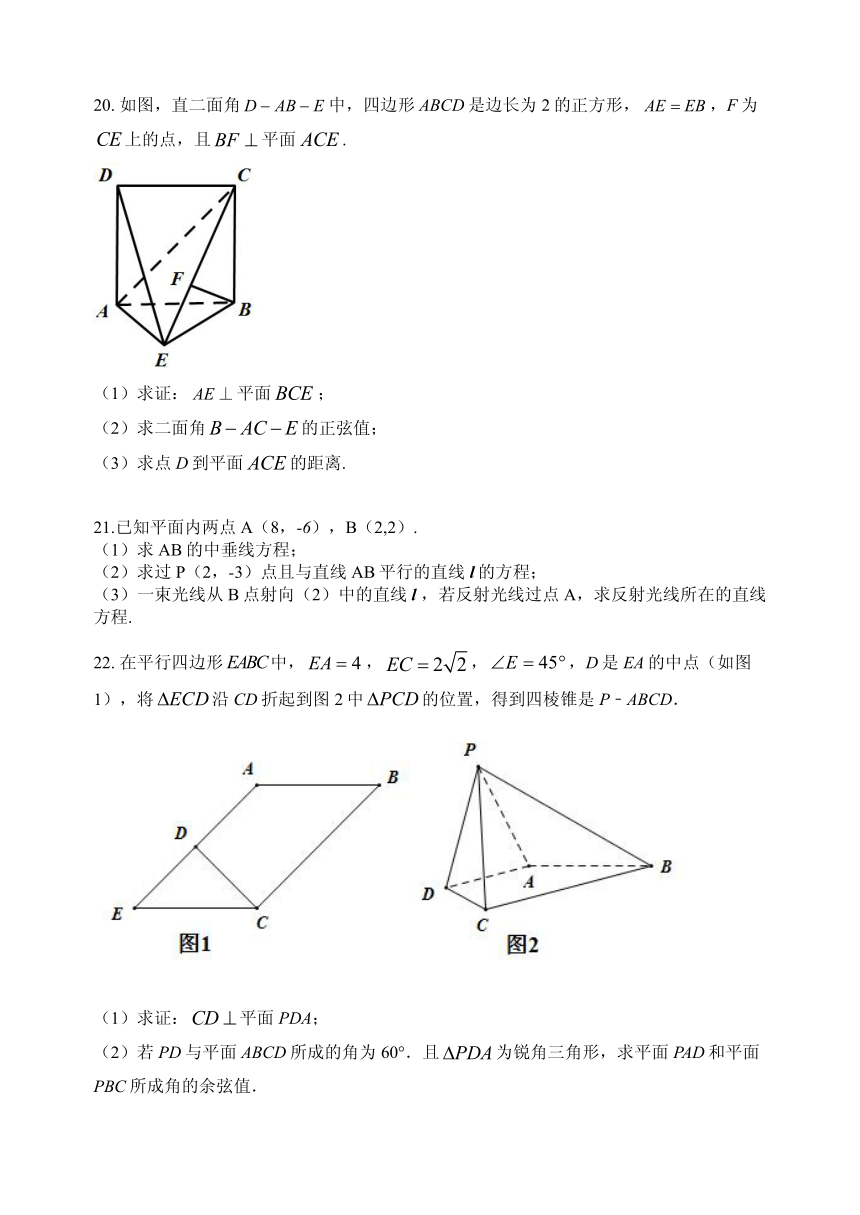
3.已知平面 的一个法向量 n 2, 2,1 ,点 A(–1,3,0)在平面 内,则点 P 2,1,4 到平
面 的距离为 ( )
A.10 B.3 C. 8 D.10
3 3
4.设 i, j,k 是空间中的一个单位正交基底,已知向量 p 8a 6b 4c,其中 a i j,
b j k , c k i ,则向量 p在基底 i, j,k 下的坐标是( )
A. 12,14,10 B. 10,12,14 C. 14,12,10 D. 4,3,2
5.如图所示,在三棱柱 ABC﹣A1B1C1中, AA1 底面
ABC, AB BC AA , π1 ABC ,点 E,F分别是棱 AB,BB2 1
的中点,则直线 EF和 BC1的夹角是( )
A. π B. π C. π D. π
6 4 3 2
6 .若空间向量a与b不共线, a b 0 c a a a,且 b,则向量 a与 c的夹角为( )
a b
A.0 B. C. D.
6 3 2
7.已知 a b 2, 2,2 3 ,a b 0, 2,0 ,则 cos a,b ( )
A. 1 B. 1 C. 6 D. 6
3 6 3 6
8.如图,在四面体 OABC 中,OA 8, AB 6, AC 4,
BC 5, OAC 45 , OAB 60 ,则 OA 与 BC 所成
角的余弦值为( )
3 2 2 2 2 1
A. B. C.
5 6 2
二、选择题(本题共 4 道小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多
项符合题目要求.全部选对的得 5 分,有选错的得 0 分,部分选对的得 2 分.)
9.(多选题)关于直线 l : 3x y 1 0,下列说法正确的有( )
A.过点( 3,-2) B. 斜率为 3 C.倾斜角为 60° D.在 y轴上的截距为 1
10.(多选题)若直线过点 A 1,2 ,且在两坐标轴上截距的绝对值相等,则直线 l方程可
能为( )
A. x y 1 0 B. x y 3 0 C. 2x y 0 D. x y 1 0
11.(多选题)已知直线 l1 、 l2 的方向向量分别是 AB (2,4, x),CD (2, y, 2),
若 | AB | 6且 l1 l2,则 x y的值可以是 ( )
A. 3 B. 1 C.1 D.3
12.(多选题)如图,在四棱锥 P﹣ABCD中,底面 ABCD为菱形,且 DAB 60 ,侧
面 PAD为正三角形,且平面 PAD 平面 ABCD,则下列说法正确的是( )
A.在棱 AD上存在点 M,使 AD 平面 PMB
B. 异面直线 AD与 PB所成的角为 90°
C. 二面角 P BC A的大小为 45°
D. BD 平面 PAC
三、填空题(本题共 4 道小题,每小题 5 分,共 20 分)
13.在长方体 ABCD﹣A1B1C1D1中, AA1 AB 2, AD 1,点 F ,G分别是 AB,CC1的中
点,则点 D1到直线GF 的距离为 ▲ .
14.已知直线 l1:ax+2y﹣3=0和直线 l2:(1﹣a)x+y+1=0.若 l1⊥l2,则实数 a的值为
▲ ;若 l1∥l2,则实数 a的值为 ▲ .
15.若直线方程ax +by +c = 0的一个法向量为 ( 3, 1),则此直线的倾斜角为 ▲ .
16.已知直线 l经过点 P 1,0 且与以 A 2,1 , B 3, 2 为端点的线段 AB有公共点,则
直线 l 的倾斜角的取值范围为 ▲ .
四、解答题(本题共 6 道小题,共 70 分.解答应写出文字说明、证明过程或演算步
骤)
17.已知直线mx y 3m 1 0恒过定点 A.
(1)若直线 l经过点 A且与直线 2x y 5 0垂直,求直线 l的方程;
(2)若直线 l经过点 A且坐标原点到直线 l的距离等于 3,求直线 l的方程.
18.已知△ABC 的三个顶点是 A(3,0),B(4,5),C(0,7)
(1)求 BC 边上的高所在的直线方程(请用直线的一般方程表示解题结果)
(2)求 BC 边上的中线所在的直线方程(请用直线的一般方程表示解题结果)
19.如图,OA,OB,OC 两两垂直,OA OC 3,OB 2,M 为 OB的中点,点 N在线段 AC
上, AN 2NC .
(1)求 MN的长;
(2) P BC BP若点 在线段 上,设 ,当 AP MN 时,求实数 的值.
PC
20.如图,直二面角D AB E中,四边形 ABCD是边长为 2的正方形, AE EB,F为
CE上的点,且BF 平面 ACE .
(1)求证: AE⊥平面 BCE;
(2)求二面角B AC E的正弦值;
(3)求点 D到平面 ACE的距离.
21.已知平面内两点 A(8,-6),B(2,2).
(1)求 AB的中垂线方程;
(2)求过 P(2,-3)点且与直线 AB平行的直线 l的方程;
(3)一束光线从 B点射向(2)中的直线 l,若反射光线过点 A,求反射光线所在的直线
方程.
22.在平行四边形 EABC中, EA 4, EC 2 2, E 45 ,D是 EA的中点(如图
1),将 ECD沿 CD折起到图 2中 PCD的位置,得到四棱锥是 P﹣ABCD.
(1)求证:CD 平面 PDA;
(2)若 PD与平面 ABCD所成的角为 60°.且 PDA为锐角三角形,求平面 PAD和平面
PBC所成角的余弦值.
曲阜一中高二数学 10 月份月考
试卷答案
1-8:BCDAC DCA
9.BC 10.ABC 11.AC 12.ABC
12.【详解】如图,取 AD 的中点 M ,连接 PM ,BM ,∵侧面 PAD 为正三角形,
PM AD ,又底面 ABCD 是菱形, DAB 60
, ABD 是等边三角形,
AD BM ,又 PM BM M , PM ,BM 平面 PMB,
AD 平面 PMB, AD PB,故 A,B正确;
对于 C,∵平面 PBC 平面 ABCD BC,BC //AD, BC 平面 PMB,
BC PB ,BC BM , PBM 是二面角 P BC A的平面角,
设 AB 1,则 BM 3 3 , PM ,
2 2
在 Rt△PBM 中, tan PBM
PM
1,即 PBM 45 ,故二面角 P BC A的
BM
大小为 45 ,故 C正确;
对于 D,假设 BD 平面 PAC,则 BD PA,又依题意平面 PAD 平面 ABCD,
AD BM ,则 BM 平面 PAD,故 BM PA,而 BD,BM相交,且在平面 ABCD
内,故 PA 平面 ABCD,与 PM 平面 ABCD矛盾,因此 BD与平面PAC不垂直,
故D错误.
故选:ABC.
13. 42
3
2
14.﹣1或 2;
3
15.
3
16.[0, ] [3 , )
4 4
17.【解】直线mx y 3m 1 0可化为m x 3 y 1 0,
x 3 0 x 3
由 可得 ,所以点 A的坐标为 3,1 .
y 1 0 y 1
(Ⅰ)设直线 l的方程为 x 2y n 0,
将点 A 3,1 代入方程可得 n 1,所以直线 l的方程为 x 2y 1 0 ,
(Ⅱ)①当直线 l斜率不存在时,因为直线过点 A,所以直线方程为 x 3,
符合原点到直线 l的距离等于 3.
②当直线 l斜率不存在时,设直线 l方程为 y kx 3k 1,即 kx y 3k 1 0
- 3k + 1 4
因为原点到直线的距离为 3,所以 = 3,解得 k
k 2 + 1 3
所以直线 l的方程为 4x 3y 15 0
综上所以直线 l的方程为 x 3或 4x 3y 15 0 .
18.解:(1)∵直线 BC 的斜率为 =﹣ ,
∴BC 边上的高所在直线的斜率为 2.
又∵直线过点 A(3,0),
∴所求直线的方程为 y﹣0=2(x﹣3),
即 2x﹣y﹣6=0,
(2)BC 边上的中点坐标为(2,6),
又∵直线过点 A(3,0),
∴所求直线的方程为 = 即 6x+y﹣18=0,
19. (1)以 O 为坐标原点,分别以OA,OB,OC 的方向为 x 轴、 y 轴、 z 轴的正方向建
立空间直角坐标系Oxyz,
则O 0,0,0 , A 3,0,0 ,B 0,2,0 ,C 0,0,3 ,
由 M 为OB的中点, AN 2NC,得M 0,1,0 ,N 1,0,2 , MN 1, 1,2 ,
MN 6,即MN 的长为 6 .
(2)设 P(0, y, z), BP ,且点 P 在线段 BC上,
PC
BP PC , 2 3 1, P 0, ,
,
1 1
AP 3, 2 , 3
1 1
,
AP MN , AP MN 0 ,
3 2 6 0, 5 .
1 1 3
20.(1)因为 BF 平面 ACE,所以 BF AE .
因为二面角 D AB E为直二面角,且CB AB,
所以CB 平面 ABE .所以CB AE .
因为 BC与BF 相交,且都属于平面BCE .
所以 AE⊥平面 BCE .
(2)以线段 AB的中点为原点O,OE所在直线为 x轴, AB所在直线为 y轴,过O点
平行于 AD的直线为 z轴,建立空间直角坐标系O xyz,如图.
因为 AE⊥面 BCE, BE 面BCE,所以 AE BE,在 Rt AEB中, AB 2,O为
AB的中点,
所以OE 1 .所以 A 0, 1,0 , E 1,0,0 ,C 0,1,2 , AE 1,1,0 , AC 0,2,2 .
设平面 AEC的一个法向量为 n x, y, z .
AE n 0, x y 0, y x,
则 即 化简得2y 2z 0, AC n 0, y z,
令 x 1,得 n 1, 1,1 是平面 AEC的一个法向量.
又平面 BAC的一个法向量为m 1,0,0 ,
cos m,n m n 1 3 .
m n 3 3
所以二面角 B AC E 6的正弦值为 .
3
(3)因为 AD//z轴, AD 2,所以 AD 0,0,2 ,
AD n 2 2
所以点D到平面 ACE的距离 d 33 3 .n
8 2
5 6 2 2
21.(Ⅰ) 2 , 2 ,∴ AB的中点坐标为 (5, 2)
k 6 2 4 3AB 8 2 3 ,∴ AB的中垂线斜率为 4
∴ AB的中垂线方程为3x 4y 23 0
y 3 4 (x 2)
(Ⅱ)由点斜式 3 ∴直线 l的方程 4x 3y 1 0
(Ⅲ)设 B(2, 2) 关于直线 l的对称点 B (m, n)
n 2 3 m 14 8 m 2 4 5 6
5 11
4 m 2 3 n 2
8 kB A
1 0 n
B (
14 8
, ) 8 14 27
∴ 2 2 .解 5 ∴ 5 5 , 5
y 11 6 (x 8)
由点斜式可得 27 ,整理得11x 27 y 74 0
22.【解】(1)将 ECD沿 CD折起过程中,CD 平面 PDA成立.证明如下:
D是 EA的中点, EA 4, DE DA 2,
在△EDC中,由余弦定理得,
CD2 EC 2 ED2 2EC 2 cos 45 8 4 2 2 2 2 4,
2
CD 2 ED,
CD2 DE 2 8 EC 2 ,
△EDC 为等腰直角三角形且CD EA,
CD DA,CD PD, PD AD D,
CD 平面 PDA.
(2)由(1)知CD 平面 PDA,CD 平面 ABCD,
平面 PDA 平面 ABCD,
PDA为锐角三角形,
P在平面 ABCD内的射影必在棱 AD上,记为 O,连接 PO, PO 平面 ABCD,
则 PDA是 PD与平面 ABCD所成的角,
PDA 60 ,
DP DA 2,
PDA为等边三角形,O为 AD的中点,
故以 O为坐标原点,过点 O且与 CD平行的直线为 x轴,
DA所在直线为 y轴,OP所在直线为 z轴建立如图所示的空间直角坐标系,
设 x轴与 BC交于点 M,
DA PA 2, OP 3
易知OD OA CM 1
BM 3,
则 P 0,0, 3 ,D 0, 1,0 ,C 2, 1,0 , B 2,3,0 ,
DC 2,0,0 ,BC 0, 4,0 , PC 2, 1, 3 ,
CD 平面 PDA,
可取平面 PDA的一个法向量 n1 1,0,0 ,
设平面 PBC的法向量 n2 x2 , y2 , z2 ,
n
BC 0 4y2 0,
则
n
,即 ,
PC 0 2x2 y2 3z2 0
3
令 z2 1,则 n2 , 0,1 为平面 PBC的一个法向量,
2
设平面 PAD和平面 PBC所成的角为 ,
3
n1 n2 21
cos cos n1,n2 2 .
n n 71 2 1 7
2
21平面 PAD和平面 PBC所成角的余弦值为 .
7
数学试卷
一、选择题(本题共 8 道小题,每小题 5 分,共 40 分)
1.经过点(1,0),且斜率为 2的直线的方程是( )
A. 2x y 2 0 B. 2x y 2 0 C. x 2y 1 0 D. x 2y 1 0
2.两平行直线 kx 6y 2 0与 4x 3y 4 0之间的距离为 ( )
1 2 6
A. B. C. 1 D.
5 5 5
3.已知平面 的一个法向量 n 2, 2,1 ,点 A(–1,3,0)在平面 内,则点 P 2,1,4 到平
面 的距离为 ( )
A.10 B.3 C. 8 D.10
3 3
4.设 i, j,k 是空间中的一个单位正交基底,已知向量 p 8a 6b 4c,其中 a i j,
b j k , c k i ,则向量 p在基底 i, j,k 下的坐标是( )
A. 12,14,10 B. 10,12,14 C. 14,12,10 D. 4,3,2
5.如图所示,在三棱柱 ABC﹣A1B1C1中, AA1 底面
ABC, AB BC AA , π1 ABC ,点 E,F分别是棱 AB,BB2 1
的中点,则直线 EF和 BC1的夹角是( )
A. π B. π C. π D. π
6 4 3 2
6 .若空间向量a与b不共线, a b 0 c a a a,且 b,则向量 a与 c的夹角为( )
a b
A.0 B. C. D.
6 3 2
7.已知 a b 2, 2,2 3 ,a b 0, 2,0 ,则 cos a,b ( )
A. 1 B. 1 C. 6 D. 6
3 6 3 6
8.如图,在四面体 OABC 中,OA 8, AB 6, AC 4,
BC 5, OAC 45 , OAB 60 ,则 OA 与 BC 所成
角的余弦值为( )
3 2 2 2 2 1
A. B. C.
5 6 2
二、选择题(本题共 4 道小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多
项符合题目要求.全部选对的得 5 分,有选错的得 0 分,部分选对的得 2 分.)
9.(多选题)关于直线 l : 3x y 1 0,下列说法正确的有( )
A.过点( 3,-2) B. 斜率为 3 C.倾斜角为 60° D.在 y轴上的截距为 1
10.(多选题)若直线过点 A 1,2 ,且在两坐标轴上截距的绝对值相等,则直线 l方程可
能为( )
A. x y 1 0 B. x y 3 0 C. 2x y 0 D. x y 1 0
11.(多选题)已知直线 l1 、 l2 的方向向量分别是 AB (2,4, x),CD (2, y, 2),
若 | AB | 6且 l1 l2,则 x y的值可以是 ( )
A. 3 B. 1 C.1 D.3
12.(多选题)如图,在四棱锥 P﹣ABCD中,底面 ABCD为菱形,且 DAB 60 ,侧
面 PAD为正三角形,且平面 PAD 平面 ABCD,则下列说法正确的是( )
A.在棱 AD上存在点 M,使 AD 平面 PMB
B. 异面直线 AD与 PB所成的角为 90°
C. 二面角 P BC A的大小为 45°
D. BD 平面 PAC
三、填空题(本题共 4 道小题,每小题 5 分,共 20 分)
13.在长方体 ABCD﹣A1B1C1D1中, AA1 AB 2, AD 1,点 F ,G分别是 AB,CC1的中
点,则点 D1到直线GF 的距离为 ▲ .
14.已知直线 l1:ax+2y﹣3=0和直线 l2:(1﹣a)x+y+1=0.若 l1⊥l2,则实数 a的值为
▲ ;若 l1∥l2,则实数 a的值为 ▲ .
15.若直线方程ax +by +c = 0的一个法向量为 ( 3, 1),则此直线的倾斜角为 ▲ .
16.已知直线 l经过点 P 1,0 且与以 A 2,1 , B 3, 2 为端点的线段 AB有公共点,则
直线 l 的倾斜角的取值范围为 ▲ .
四、解答题(本题共 6 道小题,共 70 分.解答应写出文字说明、证明过程或演算步
骤)
17.已知直线mx y 3m 1 0恒过定点 A.
(1)若直线 l经过点 A且与直线 2x y 5 0垂直,求直线 l的方程;
(2)若直线 l经过点 A且坐标原点到直线 l的距离等于 3,求直线 l的方程.
18.已知△ABC 的三个顶点是 A(3,0),B(4,5),C(0,7)
(1)求 BC 边上的高所在的直线方程(请用直线的一般方程表示解题结果)
(2)求 BC 边上的中线所在的直线方程(请用直线的一般方程表示解题结果)
19.如图,OA,OB,OC 两两垂直,OA OC 3,OB 2,M 为 OB的中点,点 N在线段 AC
上, AN 2NC .
(1)求 MN的长;
(2) P BC BP若点 在线段 上,设 ,当 AP MN 时,求实数 的值.
PC
20.如图,直二面角D AB E中,四边形 ABCD是边长为 2的正方形, AE EB,F为
CE上的点,且BF 平面 ACE .
(1)求证: AE⊥平面 BCE;
(2)求二面角B AC E的正弦值;
(3)求点 D到平面 ACE的距离.
21.已知平面内两点 A(8,-6),B(2,2).
(1)求 AB的中垂线方程;
(2)求过 P(2,-3)点且与直线 AB平行的直线 l的方程;
(3)一束光线从 B点射向(2)中的直线 l,若反射光线过点 A,求反射光线所在的直线
方程.
22.在平行四边形 EABC中, EA 4, EC 2 2, E 45 ,D是 EA的中点(如图
1),将 ECD沿 CD折起到图 2中 PCD的位置,得到四棱锥是 P﹣ABCD.
(1)求证:CD 平面 PDA;
(2)若 PD与平面 ABCD所成的角为 60°.且 PDA为锐角三角形,求平面 PAD和平面
PBC所成角的余弦值.
曲阜一中高二数学 10 月份月考
试卷答案
1-8:BCDAC DCA
9.BC 10.ABC 11.AC 12.ABC
12.【详解】如图,取 AD 的中点 M ,连接 PM ,BM ,∵侧面 PAD 为正三角形,
PM AD ,又底面 ABCD 是菱形, DAB 60
, ABD 是等边三角形,
AD BM ,又 PM BM M , PM ,BM 平面 PMB,
AD 平面 PMB, AD PB,故 A,B正确;
对于 C,∵平面 PBC 平面 ABCD BC,BC //AD, BC 平面 PMB,
BC PB ,BC BM , PBM 是二面角 P BC A的平面角,
设 AB 1,则 BM 3 3 , PM ,
2 2
在 Rt△PBM 中, tan PBM
PM
1,即 PBM 45 ,故二面角 P BC A的
BM
大小为 45 ,故 C正确;
对于 D,假设 BD 平面 PAC,则 BD PA,又依题意平面 PAD 平面 ABCD,
AD BM ,则 BM 平面 PAD,故 BM PA,而 BD,BM相交,且在平面 ABCD
内,故 PA 平面 ABCD,与 PM 平面 ABCD矛盾,因此 BD与平面PAC不垂直,
故D错误.
故选:ABC.
13. 42
3
2
14.﹣1或 2;
3
15.
3
16.[0, ] [3 , )
4 4
17.【解】直线mx y 3m 1 0可化为m x 3 y 1 0,
x 3 0 x 3
由 可得 ,所以点 A的坐标为 3,1 .
y 1 0 y 1
(Ⅰ)设直线 l的方程为 x 2y n 0,
将点 A 3,1 代入方程可得 n 1,所以直线 l的方程为 x 2y 1 0 ,
(Ⅱ)①当直线 l斜率不存在时,因为直线过点 A,所以直线方程为 x 3,
符合原点到直线 l的距离等于 3.
②当直线 l斜率不存在时,设直线 l方程为 y kx 3k 1,即 kx y 3k 1 0
- 3k + 1 4
因为原点到直线的距离为 3,所以 = 3,解得 k
k 2 + 1 3
所以直线 l的方程为 4x 3y 15 0
综上所以直线 l的方程为 x 3或 4x 3y 15 0 .
18.解:(1)∵直线 BC 的斜率为 =﹣ ,
∴BC 边上的高所在直线的斜率为 2.
又∵直线过点 A(3,0),
∴所求直线的方程为 y﹣0=2(x﹣3),
即 2x﹣y﹣6=0,
(2)BC 边上的中点坐标为(2,6),
又∵直线过点 A(3,0),
∴所求直线的方程为 = 即 6x+y﹣18=0,
19. (1)以 O 为坐标原点,分别以OA,OB,OC 的方向为 x 轴、 y 轴、 z 轴的正方向建
立空间直角坐标系Oxyz,
则O 0,0,0 , A 3,0,0 ,B 0,2,0 ,C 0,0,3 ,
由 M 为OB的中点, AN 2NC,得M 0,1,0 ,N 1,0,2 , MN 1, 1,2 ,
MN 6,即MN 的长为 6 .
(2)设 P(0, y, z), BP ,且点 P 在线段 BC上,
PC
BP PC , 2 3 1, P 0, ,
,
1 1
AP 3, 2 , 3
1 1
,
AP MN , AP MN 0 ,
3 2 6 0, 5 .
1 1 3
20.(1)因为 BF 平面 ACE,所以 BF AE .
因为二面角 D AB E为直二面角,且CB AB,
所以CB 平面 ABE .所以CB AE .
因为 BC与BF 相交,且都属于平面BCE .
所以 AE⊥平面 BCE .
(2)以线段 AB的中点为原点O,OE所在直线为 x轴, AB所在直线为 y轴,过O点
平行于 AD的直线为 z轴,建立空间直角坐标系O xyz,如图.
因为 AE⊥面 BCE, BE 面BCE,所以 AE BE,在 Rt AEB中, AB 2,O为
AB的中点,
所以OE 1 .所以 A 0, 1,0 , E 1,0,0 ,C 0,1,2 , AE 1,1,0 , AC 0,2,2 .
设平面 AEC的一个法向量为 n x, y, z .
AE n 0, x y 0, y x,
则 即 化简得2y 2z 0, AC n 0, y z,
令 x 1,得 n 1, 1,1 是平面 AEC的一个法向量.
又平面 BAC的一个法向量为m 1,0,0 ,
cos m,n m n 1 3 .
m n 3 3
所以二面角 B AC E 6的正弦值为 .
3
(3)因为 AD//z轴, AD 2,所以 AD 0,0,2 ,
AD n 2 2
所以点D到平面 ACE的距离 d 33 3 .n
8 2
5 6 2 2
21.(Ⅰ) 2 , 2 ,∴ AB的中点坐标为 (5, 2)
k 6 2 4 3AB 8 2 3 ,∴ AB的中垂线斜率为 4
∴ AB的中垂线方程为3x 4y 23 0
y 3 4 (x 2)
(Ⅱ)由点斜式 3 ∴直线 l的方程 4x 3y 1 0
(Ⅲ)设 B(2, 2) 关于直线 l的对称点 B (m, n)
n 2 3 m 14 8 m 2 4 5 6
5 11
4 m 2 3 n 2
8 kB A
1 0 n
B (
14 8
, ) 8 14 27
∴ 2 2 .解 5 ∴ 5 5 , 5
y 11 6 (x 8)
由点斜式可得 27 ,整理得11x 27 y 74 0
22.【解】(1)将 ECD沿 CD折起过程中,CD 平面 PDA成立.证明如下:
D是 EA的中点, EA 4, DE DA 2,
在△EDC中,由余弦定理得,
CD2 EC 2 ED2 2EC 2 cos 45 8 4 2 2 2 2 4,
2
CD 2 ED,
CD2 DE 2 8 EC 2 ,
△EDC 为等腰直角三角形且CD EA,
CD DA,CD PD, PD AD D,
CD 平面 PDA.
(2)由(1)知CD 平面 PDA,CD 平面 ABCD,
平面 PDA 平面 ABCD,
PDA为锐角三角形,
P在平面 ABCD内的射影必在棱 AD上,记为 O,连接 PO, PO 平面 ABCD,
则 PDA是 PD与平面 ABCD所成的角,
PDA 60 ,
DP DA 2,
PDA为等边三角形,O为 AD的中点,
故以 O为坐标原点,过点 O且与 CD平行的直线为 x轴,
DA所在直线为 y轴,OP所在直线为 z轴建立如图所示的空间直角坐标系,
设 x轴与 BC交于点 M,
DA PA 2, OP 3
易知OD OA CM 1
BM 3,
则 P 0,0, 3 ,D 0, 1,0 ,C 2, 1,0 , B 2,3,0 ,
DC 2,0,0 ,BC 0, 4,0 , PC 2, 1, 3 ,
CD 平面 PDA,
可取平面 PDA的一个法向量 n1 1,0,0 ,
设平面 PBC的法向量 n2 x2 , y2 , z2 ,
n
BC 0 4y2 0,
则
n
,即 ,
PC 0 2x2 y2 3z2 0
3
令 z2 1,则 n2 , 0,1 为平面 PBC的一个法向量,
2
设平面 PAD和平面 PBC所成的角为 ,
3
n1 n2 21
cos cos n1,n2 2 .
n n 71 2 1 7
2
21平面 PAD和平面 PBC所成角的余弦值为 .
7
同课章节目录
