2021-2022学年数学人教A版(2019)选择性必修第一册2.3.2 两点间的距离公式课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)选择性必修第一册2.3.2 两点间的距离公式课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 383.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 21:58:12 | ||
图片预览






文档简介
(共19张PPT)
第二章 直线和圆的方程
2.3.2 两点间的距离公式
一、创设情境 引入新课
在一条笔直的公路同侧有两个大型小区,现计划在公路上某处建一个公交站点以方便居住在两个小区住户的出行。如何选址能使站点到两个小区的距离之和最小?
二、探究本质得新知
探究一:两点间的距离公式
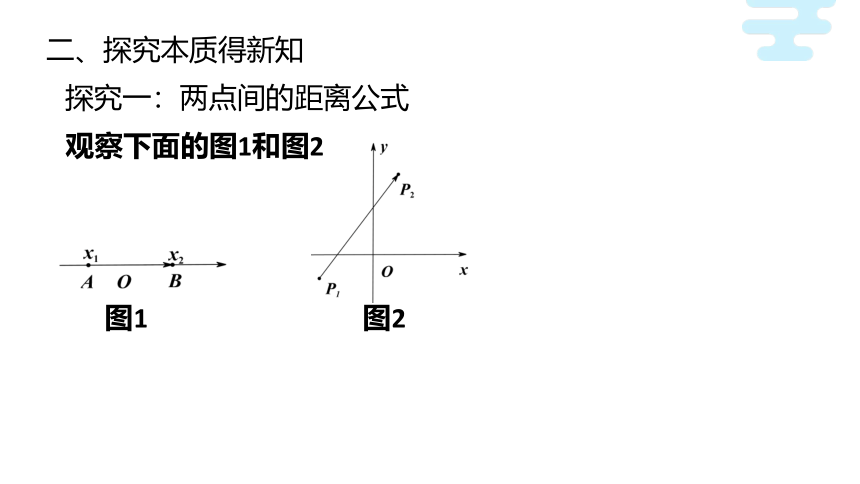
观察下面的图1和图2
图1 图2
二、探究本质得新知
探究一:两点间的距离公式
问题1:如何求图1中A、B两点间的距离?A、B两点间的距离与向量 的模有何关系?
提示:|AB|=|x2-x1|.A、B两点间的距离等于向量 的模。
问题2:图2中能否用向量 的模求出 两点间距离?
提示:可以,根据向量的知识得: ,所以 .
二、探究本质得新知
两点间的距离公式
探究一:两点间的距离公式
三、举例应用,掌握定义
例1 (1)(多选题)已知A(2,1),B(-1,b),|AB|=5,则b的值为 ( )
A.-3 B.3 C.5 D.-1
(2)已知△ABC三顶点坐标A(-3,1)、B(3,-3)、C(1,7),试判断△ABC的形状.
三、举例应用,掌握定义
【解析】(1)选AC.因为
所以 ,所以 或 .
答案:AC
三、举例应用,掌握定义
(2)因为|AB|= ,
|AC|= , 又|BC|= =2 ,
所以|AB|2+|AC|2=|BC|2,且|AB|=|AC|,
所以△ABC是等腰直角三角形.
三、举例应用,掌握定义
例2:如图所示,已知 BD是 ΔABC边 AC上的中线,建立适当的平面直角坐标系,证明: .
三、举例应用,掌握定义
【解析】如图所示,以 AC所在的直线为x 轴,点D 为坐标原点,建立平面直角坐标系xDy .设 B(b,c),C(a,0),依题意得A(-a,0) .
所以
四、学生练习,加深理解
1.已知ΔABC的顶点坐标为A(7,8),B(10,4),
C(2,-4),则BC边上的中线AM的长为()
A.8 B.13 C. 2 D.
四、学生练习,加深理解
【解析】选D.由B(10,4),C(2,-4),可得中点M(6,0),又A(7,8)
所以
四、学生练习,加深理解
2. 已知点A(-3,4)和B(0,b),且|AB|=5,则b等于( )
A.0或8 B.0或-8 C.0或6 D.0或-6
【解析】选A. 由两点间距离公式得: ,解得:b=0 或8.
四、学生练习,加深理解
3.已知点A(5,2a-1),B(a+1, a-4),当|AB|取最小值时,a=________.
【解析】|AB|=
=
=
所以当a= 时,|AB|取最小值.
答案:
四、学生练习,加深理解
4.设点A在x轴上,点B在y轴上,AB的中点是P(2,-1),则|AB|等于________.
【解析】设A(x,0),B(0,y),因为AB中点P(2,-1),所以 =2, =-1,所以x=4,y=-2,即A(4,0),B(0,-2),所以|AB|= .
答案:
四、学生练习,加深理解
5.求证:等腰梯形的对角线相等.
四、学生练习,加深理解
【证明】如图,以AB所在直线为x轴,以AB的中
点为坐标原点建立如图平面直角坐标系.
设A(-a,0)、D(b,c),由等腰梯形的性质知
B(a,0),C(-b,c).
则|AC|=
|BD|=
所以|AC|=|BD|.即等腰梯形的对角线相等.
1.知识方面:(1)掌握了平面内两点间的距离公式。
(2)能够利用两点间的距离公式解决平面几何中的有关问题
2.能力方面:能够用所学知识解决一些实际问题。
3.思想方面:体升了数学运算素养和数形结合的能力
五、归纳小结 提高认识
六、作业布置 检测目标
教材P79 习题4,5题
第二章 直线和圆的方程
2.3.2 两点间的距离公式
一、创设情境 引入新课
在一条笔直的公路同侧有两个大型小区,现计划在公路上某处建一个公交站点以方便居住在两个小区住户的出行。如何选址能使站点到两个小区的距离之和最小?
二、探究本质得新知
探究一:两点间的距离公式
观察下面的图1和图2
图1 图2
二、探究本质得新知
探究一:两点间的距离公式
问题1:如何求图1中A、B两点间的距离?A、B两点间的距离与向量 的模有何关系?
提示:|AB|=|x2-x1|.A、B两点间的距离等于向量 的模。
问题2:图2中能否用向量 的模求出 两点间距离?
提示:可以,根据向量的知识得: ,所以 .
二、探究本质得新知
两点间的距离公式
探究一:两点间的距离公式
三、举例应用,掌握定义
例1 (1)(多选题)已知A(2,1),B(-1,b),|AB|=5,则b的值为 ( )
A.-3 B.3 C.5 D.-1
(2)已知△ABC三顶点坐标A(-3,1)、B(3,-3)、C(1,7),试判断△ABC的形状.
三、举例应用,掌握定义
【解析】(1)选AC.因为
所以 ,所以 或 .
答案:AC
三、举例应用,掌握定义
(2)因为|AB|= ,
|AC|= , 又|BC|= =2 ,
所以|AB|2+|AC|2=|BC|2,且|AB|=|AC|,
所以△ABC是等腰直角三角形.
三、举例应用,掌握定义
例2:如图所示,已知 BD是 ΔABC边 AC上的中线,建立适当的平面直角坐标系,证明: .
三、举例应用,掌握定义
【解析】如图所示,以 AC所在的直线为x 轴,点D 为坐标原点,建立平面直角坐标系xDy .设 B(b,c),C(a,0),依题意得A(-a,0) .
所以
四、学生练习,加深理解
1.已知ΔABC的顶点坐标为A(7,8),B(10,4),
C(2,-4),则BC边上的中线AM的长为()
A.8 B.13 C. 2 D.
四、学生练习,加深理解
【解析】选D.由B(10,4),C(2,-4),可得中点M(6,0),又A(7,8)
所以
四、学生练习,加深理解
2. 已知点A(-3,4)和B(0,b),且|AB|=5,则b等于( )
A.0或8 B.0或-8 C.0或6 D.0或-6
【解析】选A. 由两点间距离公式得: ,解得:b=0 或8.
四、学生练习,加深理解
3.已知点A(5,2a-1),B(a+1, a-4),当|AB|取最小值时,a=________.
【解析】|AB|=
=
=
所以当a= 时,|AB|取最小值.
答案:
四、学生练习,加深理解
4.设点A在x轴上,点B在y轴上,AB的中点是P(2,-1),则|AB|等于________.
【解析】设A(x,0),B(0,y),因为AB中点P(2,-1),所以 =2, =-1,所以x=4,y=-2,即A(4,0),B(0,-2),所以|AB|= .
答案:
四、学生练习,加深理解
5.求证:等腰梯形的对角线相等.
四、学生练习,加深理解
【证明】如图,以AB所在直线为x轴,以AB的中
点为坐标原点建立如图平面直角坐标系.
设A(-a,0)、D(b,c),由等腰梯形的性质知
B(a,0),C(-b,c).
则|AC|=
|BD|=
所以|AC|=|BD|.即等腰梯形的对角线相等.
1.知识方面:(1)掌握了平面内两点间的距离公式。
(2)能够利用两点间的距离公式解决平面几何中的有关问题
2.能力方面:能够用所学知识解决一些实际问题。
3.思想方面:体升了数学运算素养和数形结合的能力
五、归纳小结 提高认识
六、作业布置 检测目标
教材P79 习题4,5题
