七年级下册数学第七章三角形全章导学案(无答案)
文档属性
| 名称 | 七年级下册数学第七章三角形全章导学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 113.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-27 09:19:19 | ||
图片预览



文档简介
七年级下册数学 第七章 三角形
导学1 7.1.1 三角形的边
一、学习目标:
1.了解三角形的概念及其基本元素。
2.理解三角形三边之间的关系。
二、自主学习
认真阅读课本第63页——64页上面,解决以下问题:
举出几个日常生活中三角形的例子。
由______________的三条线段______相接所组成得图形叫做三角形。
如图,三角形的三边分别是________或______,
三角形的内角分别是__________,
三角形的顶点分别是_______ ,
这个三角形记作______,读作____________. (第3题)
4._______________的三角形叫等边三角形,_____________的三角形叫等腰三角形,_______________的三角形叫不等边三角形。在等腰三角形中,__________都叫腰,______叫底,______________叫底角 ,_____________叫顶角。
如图,在等腰⊿ABC中,AB=AC,
______________是腰,_____是底边,
______是顶角,_______是底角。 ( 第4题)
5.按“几条边相等”分类,三角形分为_______、________和__________,等腰三角形又分为_________和_________。按角的大小分类,三角形分为______、________、___________。
三、合作探究
1.课本第64页探究。
2. 课本第64页例题。
3.有2厘米和5厘米的小棒各一根,再配一根8厘米的小棒,能围成一个三角形吗?换成3厘米的呢?要想组成三角形,第三根小棒的长度应在什么范围内?
四、巩固提高
1.三角形任意两边的和____第三边,任意两边的差_____第三边。
如图,在三角形ABC中,AB+BC____AC,
AC+BC____AB, AB-AC___BC.
( 第1题)
2.课本第65页
3. 课本 第65页
4.课本 第69页
七年级下册数学 第七章 三角形
导学2 7.1.2三角形的高、中线、角平分线
一、学习目标:
1、会画三角形的高、中线、角平分线。
2、理解三角形的高、中线、角平分线的简单性质。
二、自主学习
阅读课本第65页----66页,回答下列问题:(注意三角形的高、中线、角平分线的作法)
从⊿ABC的顶点A向__________作垂线,垂足为D,所得线段AD叫⊿ABC的边BC上的高。
连接⊿ABC顶点A和_______________,所得线段AD叫⊿ABC的边BC上的中线。
画∠A的平分线AD,交___于D,所得线段AD叫⊿ABC的角平分线。
三角形的三条高、三条中线、三条角平分线都是______。(线段、直线、射线)
课本第66页 练习第1题。
6. 课本第66页 练习第1题。
7.课本第69页 第3题。
三、合作探究
1.三角形的三条高相交于一点吗?锐角三角形、直接三角形、钝角三角形他们的三条高各交于什么位置?
2.三角形的三条中线、三条角平分线也分别相交于一点吗?交点在什么位置?
四、巩固提高
1.下列说法错误的是( )
A.三角形的三条高一定在三角形的内部交于一点。
B.三角形的三条中线一定在三角形的内部交于一点。
C.三角形的角平分线一定在三角形的内部交于一点。
D.三角形的三条高可能相交于三角形外部一点。
2.能把一个三角形分成面积相等的两个小三角形的是这个三角形的( )
A.角平分线 B. 高 C.边的中垂线 D.中线
3.如图所示,
因为AD是⊿ABC的角平分线,
所以∠___=∠___=∠_____,
因为BE是⊿ABC的高,
所以BE__AC或∠____=∠____=90°,
因为CF是⊿ABC的中线, (第3题)
所以_______=________。
4.课本第70页第9题
七年级下册数学 第七章 三角形
导学3 7.1.3三角形的稳定性
一、学习目标:
1、掌握三角形的稳定性。
2、认识生活实际中的运用。
二、自主学习
快速阅读课本第67页——68页后,回答以下问题:
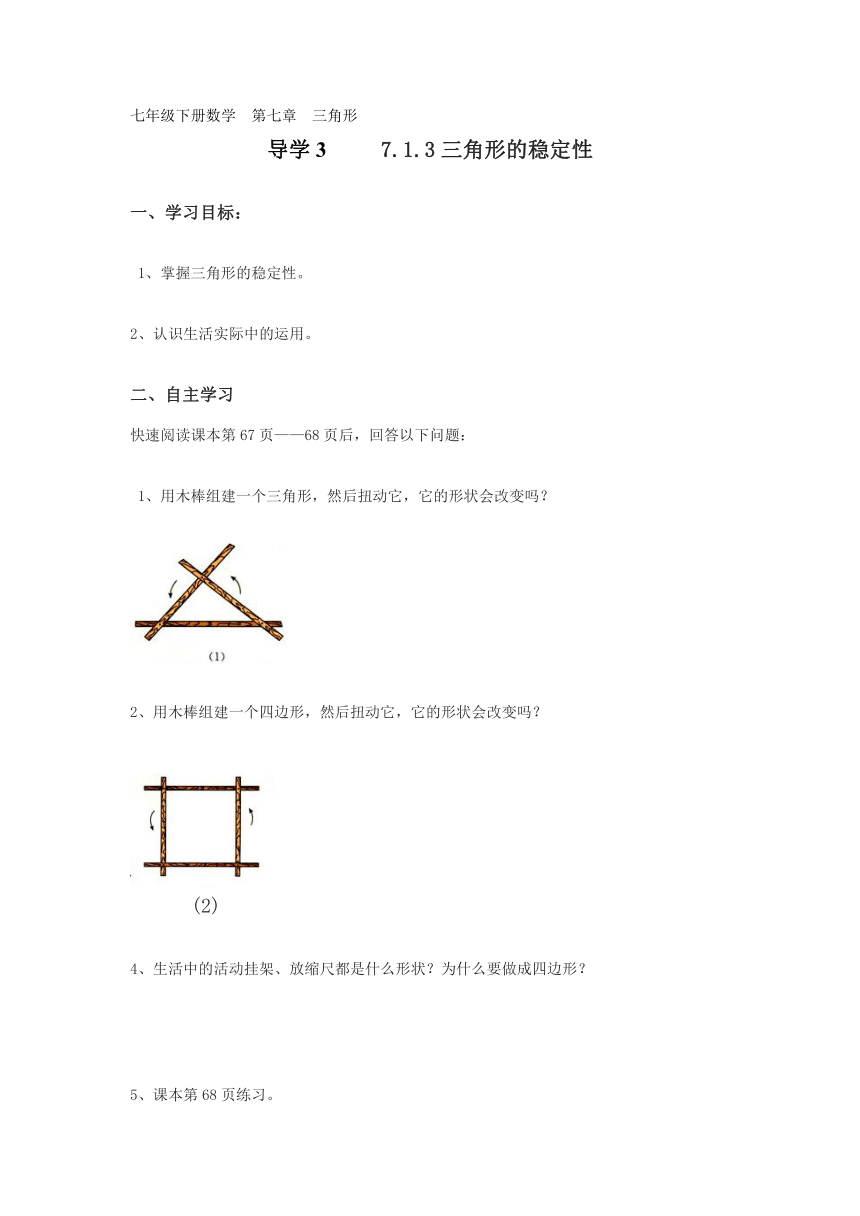
1、用木棒组建一个三角形,然后扭动它,它的形状会改变吗?
2、用木棒组建一个四边形,然后扭动它,它的形状会改变吗?
(2)
4、生活中的活动挂架、放缩尺都是什么形状?为什么要做成四边形?
5、课本第68页练习。
三、合作探究
1、比一比,举例说明生活中哪些要用到三角形的稳定性,哪些要用到四边形的不稳定性?
2、想一想,用什么方法能使不稳定的四边形变的稳定。
3、做一做,如何使损坏的凳子修好?
四、巩固提高
1、四边形易变形是优点还是缺点?
2、课本第70页第10题 。
七年级下册数学 第七章 三角形
导学4 7.2.1三角形的内角
学习目标
学会三角形的内角和定理及其证明
会利用三角形的内角和定理求教的度数
自主学习
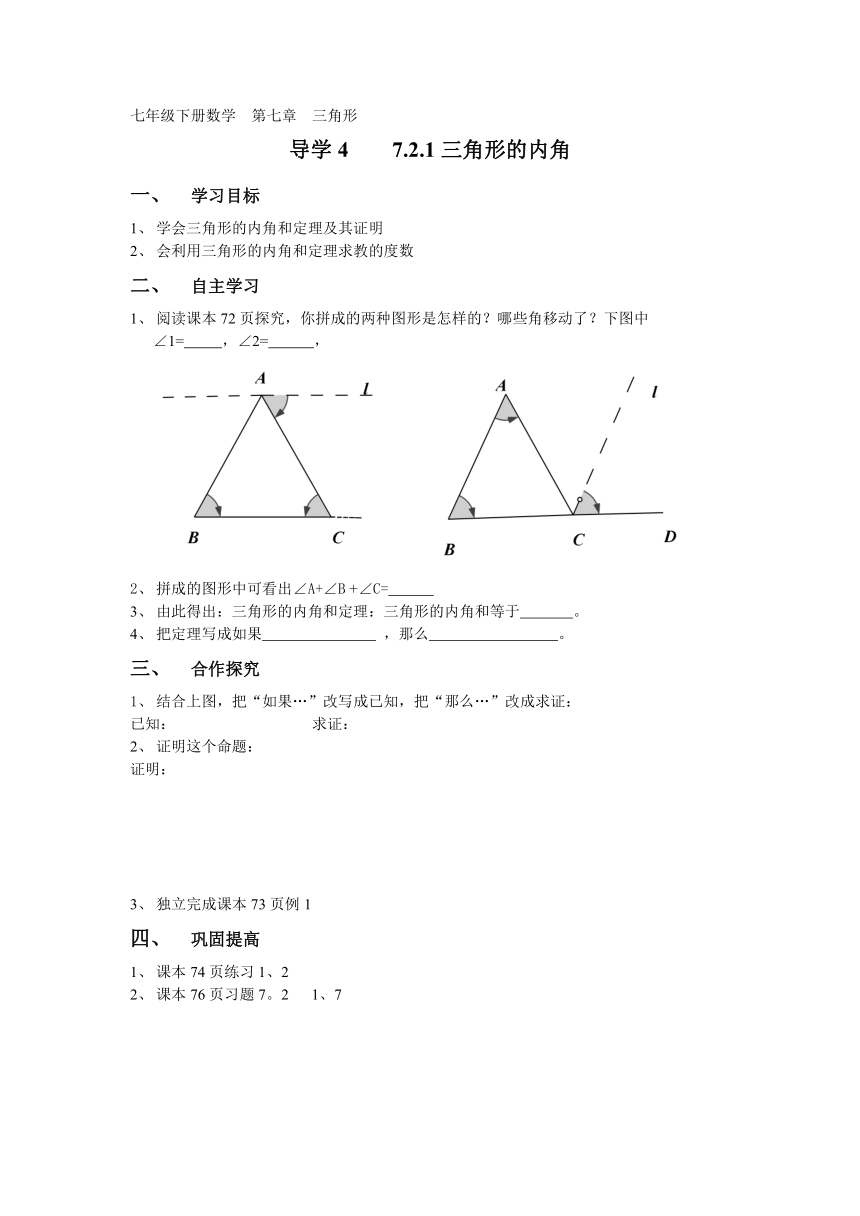
阅读课本72页探究,你拼成的两种图形是怎样的?哪些角移动了?下图中
∠1= ,∠2= ,
拼成的图形中可看出∠A+∠B +∠C=
由此得出:三角形的内角和定理:三角形的内角和等于 。
把定理写成如果 ,那么 。
合作探究
结合上图,把“如果…”改写成已知,把“那么…”改成求证:
已知: 求证:
证明这个命题:
证明:
独立完成课本73页例1
巩固提高
课本74页练习1、2
课本76页习题7。2 1、7
七年级下册数学 第七章 三角形
导学5 7.2.2三角形的外角
学习目标
理解三角形外角的定义
学会三角形外角的性质及其推论
自主学习
1、阅读课文填空:三角形的 与 组成的角,叫做三角形的外角。
2、下面图形中的角是三角形的外角吗?
探究三角形外交的性质:课本74页
结论:三角形的一个外角等于 。
可改为如果 ,那么 。
合作探究 课本75页例2
巩固提高
课本75页练习
(1)一个三角形最多有几个直角;最多有几个钝角?为什么?
(2)直角三角形的外角可以是锐角吗?为什么?
CE是 ABC的外角∠ACD的平分线,且CE交BA延长线于点E,证明:∠BAC>∠B
七年级下册数学 第七章 三角形
导学6 7.3.1多边形
学习目标
认识多边形及其有关概念
会计算多边形的对角线的条数
自主学习
阅读课文填空:
(1)在平面内, 叫做多边形。
(2)如果一个多边形由 条线段组成,那么这个多边形就叫做 边形,
是最简单的多边形。
叫做多边形的内角。
叫做多边形的外角。
叫做多边形的对角线。
(6)如果 ,那么这个多边形就是凸多边形。
(7) 叫做正多边形。
三、合作探究
1、课本81页练习1、2;
2、从六边形的一个顶点出发可以画出几条对角线?他们将六边形分成几个三角形?
七边形呢?
由此你能得出多边形对角线条数与它的变数的关系吗?
一个八边形,它有 条对角线。
四、巩固提高
课本84页习题7.3 1、
七年级下册数学 第七章 三角形
导学7 7.3.1多边形的内角和
学习目标
会计算多边形的内角和
会计算多边形的外角和
会利用内角和、外角和求多边形的边数
自主学习
1、从n边形的一个顶点可以画 条对角线,它们可以将n边形分成 个三角形?
2、阅读课本81—82页
3、n边形的内角和等于
4、做课本83页练习1(1)(2)(4)
5、做课本84页习题7.3 2、4
三、合作探究
1、课本82页例1
2、课本82页例2
3、多边形的外角和等于
4、做课本84页练习1(3)
四、巩固提高
1、一个多边形的格内角都等于120度,它是几边形?
2、一个多边形的内角和与外角和相等,它是几边形?
3、课本85页5、6题
七年级下册数学 第七章 三角形
导学 8 复习 三角形 (一)
学习目标:
理解并掌握本章有关概念及性质。
会用本章知识解决问题。
自主学习:
阅读课本第七章内容,回答下列问题:
有关概念
什么叫三角形?三角形的高、中线、角平分线?
什么叫多边形?多边形的对角线?
什么叫平面镶嵌?
有关性质:
三角形三边的关系?
三角形、多边形的内角和?外角和?
3. 三角形外角的性质?
用一种或两种正多边形进行平面镶嵌的条件是什么?
合作探究:
先独立完成下列问题,再小组交流
1. 以下列各组线段长为边能构成三角形的是( )
(A) 7. 12. 5 (B) 6. 8. 15 (C) 4. 5. 3 (D) 8. 3. 4
2. 在△ABC中,若∠C=90 ∠CAB与∠CBA的平分线相交于点O,则∠AOB=( )
(A) 105 (B)120 (C)135 (D)150
3. 如图,∠BOC=100 ∠C=20 ∠B=25 ,则∠A=( )
4. 正三角形、正四边形、正五边形、正六边形、正八边形,在选择其中一种正多边形进行平面镶嵌,可选择的是 。
巩固提高:
1. 已知:△ABC中, AD⊥BC于D,∠DAC=∠C,∠B=65
则∠BAC= 。
2. 如图,已知 ∠B=42 ∠A+10 =∠C AB∥C
则 ∠ACD=
3. 如果一个凸多边形从一个顶点引出的对角线条数为4, 则这个多边形为 边形, 内角和
是 。
4. 如图,在小河的一边开两条小渠,设计要求两条水渠成45 角,有人采取这样的方法:在两个水渠内侧各取一点E F 之后连起来,并测得∠CEF=100 ∠BFE=55 .问这条水渠是否符合要求?并说明理由。
七年级下册数学 第七章 三角形
导学9 复习三角形 专题训练 (二)
一、 学习目标:
1. 学会分析解题思路
2. 学会用本章知识解决实际问题
二、 自主学习:
专题①: 与三角形有关的线段:
三角形的高构造了 条件, 三角形的中线隐含了 相等的条件。
将三角形面积分成 两部分, 三角形的角平分线提供了
相等条件。
专题②: 三角形内角和及外角的性质
三角形内角和与外角性质为解题提供了隐含条件,可解决许多有关三角形 问题。
专题③: 多边形内角和及外角和
求多边形的内角、外角、边数及对角线问题时,常用到多边形的公式是 。
专题④: 平面镶嵌
常用的平面镶嵌大多是 的镶嵌, 主要限于用 种正多边形镶嵌和允许用 种正多边形镶嵌两种类型
三、 合作探究
1. 如图(1),在△ABC中,AD、AE分别是BC边的中线和高,AB=10, AC=6
则△ABD与△ACD的周长之差
是 面积关系是
2. 如图(2),已知△ABC中,D在BC的延长线上,E在CA的延长线上,F在AB上,则∠2 ∠1 (填“<”或“=”或“>”)
3. 已知,一个多边形内角和是外角和的2.5倍,则此多边形的边数为 。
4. 三角形最长边等于10,另外两边长分别为X和4,周长为C,则X的取值范围是 C的取值范围是 。
四、 巩固提高:
1. 如图(4),在△ABC中,AD是高,AE 是∠BAC的角平分线,∠B=20 , ∠C=60 ,求∠DAE的度数
2. 某校欲建一座足球场,现有正三角形、正六边形、正八边形、正十边形五种形状的草皮,请你帮助选择两种草皮来铺满足球场
导学1 7.1.1 三角形的边
一、学习目标:
1.了解三角形的概念及其基本元素。
2.理解三角形三边之间的关系。
二、自主学习
认真阅读课本第63页——64页上面,解决以下问题:
举出几个日常生活中三角形的例子。
由______________的三条线段______相接所组成得图形叫做三角形。
如图,三角形的三边分别是________或______,
三角形的内角分别是__________,
三角形的顶点分别是_______ ,
这个三角形记作______,读作____________. (第3题)
4._______________的三角形叫等边三角形,_____________的三角形叫等腰三角形,_______________的三角形叫不等边三角形。在等腰三角形中,__________都叫腰,______叫底,______________叫底角 ,_____________叫顶角。
如图,在等腰⊿ABC中,AB=AC,
______________是腰,_____是底边,
______是顶角,_______是底角。 ( 第4题)
5.按“几条边相等”分类,三角形分为_______、________和__________,等腰三角形又分为_________和_________。按角的大小分类,三角形分为______、________、___________。
三、合作探究
1.课本第64页探究。
2. 课本第64页例题。
3.有2厘米和5厘米的小棒各一根,再配一根8厘米的小棒,能围成一个三角形吗?换成3厘米的呢?要想组成三角形,第三根小棒的长度应在什么范围内?
四、巩固提高
1.三角形任意两边的和____第三边,任意两边的差_____第三边。
如图,在三角形ABC中,AB+BC____AC,
AC+BC____AB, AB-AC___BC.
( 第1题)
2.课本第65页
3. 课本 第65页
4.课本 第69页
七年级下册数学 第七章 三角形
导学2 7.1.2三角形的高、中线、角平分线
一、学习目标:
1、会画三角形的高、中线、角平分线。
2、理解三角形的高、中线、角平分线的简单性质。
二、自主学习
阅读课本第65页----66页,回答下列问题:(注意三角形的高、中线、角平分线的作法)
从⊿ABC的顶点A向__________作垂线,垂足为D,所得线段AD叫⊿ABC的边BC上的高。
连接⊿ABC顶点A和_______________,所得线段AD叫⊿ABC的边BC上的中线。
画∠A的平分线AD,交___于D,所得线段AD叫⊿ABC的角平分线。
三角形的三条高、三条中线、三条角平分线都是______。(线段、直线、射线)
课本第66页 练习第1题。
6. 课本第66页 练习第1题。
7.课本第69页 第3题。
三、合作探究
1.三角形的三条高相交于一点吗?锐角三角形、直接三角形、钝角三角形他们的三条高各交于什么位置?
2.三角形的三条中线、三条角平分线也分别相交于一点吗?交点在什么位置?
四、巩固提高
1.下列说法错误的是( )
A.三角形的三条高一定在三角形的内部交于一点。
B.三角形的三条中线一定在三角形的内部交于一点。
C.三角形的角平分线一定在三角形的内部交于一点。
D.三角形的三条高可能相交于三角形外部一点。
2.能把一个三角形分成面积相等的两个小三角形的是这个三角形的( )
A.角平分线 B. 高 C.边的中垂线 D.中线
3.如图所示,
因为AD是⊿ABC的角平分线,
所以∠___=∠___=∠_____,
因为BE是⊿ABC的高,
所以BE__AC或∠____=∠____=90°,
因为CF是⊿ABC的中线, (第3题)
所以_______=________。
4.课本第70页第9题
七年级下册数学 第七章 三角形
导学3 7.1.3三角形的稳定性
一、学习目标:
1、掌握三角形的稳定性。
2、认识生活实际中的运用。
二、自主学习
快速阅读课本第67页——68页后,回答以下问题:
1、用木棒组建一个三角形,然后扭动它,它的形状会改变吗?
2、用木棒组建一个四边形,然后扭动它,它的形状会改变吗?
(2)
4、生活中的活动挂架、放缩尺都是什么形状?为什么要做成四边形?
5、课本第68页练习。
三、合作探究
1、比一比,举例说明生活中哪些要用到三角形的稳定性,哪些要用到四边形的不稳定性?
2、想一想,用什么方法能使不稳定的四边形变的稳定。
3、做一做,如何使损坏的凳子修好?
四、巩固提高
1、四边形易变形是优点还是缺点?
2、课本第70页第10题 。
七年级下册数学 第七章 三角形
导学4 7.2.1三角形的内角
学习目标
学会三角形的内角和定理及其证明
会利用三角形的内角和定理求教的度数
自主学习
阅读课本72页探究,你拼成的两种图形是怎样的?哪些角移动了?下图中
∠1= ,∠2= ,
拼成的图形中可看出∠A+∠B +∠C=
由此得出:三角形的内角和定理:三角形的内角和等于 。
把定理写成如果 ,那么 。
合作探究
结合上图,把“如果…”改写成已知,把“那么…”改成求证:
已知: 求证:
证明这个命题:
证明:
独立完成课本73页例1
巩固提高
课本74页练习1、2
课本76页习题7。2 1、7
七年级下册数学 第七章 三角形
导学5 7.2.2三角形的外角
学习目标
理解三角形外角的定义
学会三角形外角的性质及其推论
自主学习
1、阅读课文填空:三角形的 与 组成的角,叫做三角形的外角。
2、下面图形中的角是三角形的外角吗?
探究三角形外交的性质:课本74页
结论:三角形的一个外角等于 。
可改为如果 ,那么 。
合作探究 课本75页例2
巩固提高
课本75页练习
(1)一个三角形最多有几个直角;最多有几个钝角?为什么?
(2)直角三角形的外角可以是锐角吗?为什么?
CE是 ABC的外角∠ACD的平分线,且CE交BA延长线于点E,证明:∠BAC>∠B
七年级下册数学 第七章 三角形
导学6 7.3.1多边形
学习目标
认识多边形及其有关概念
会计算多边形的对角线的条数
自主学习
阅读课文填空:
(1)在平面内, 叫做多边形。
(2)如果一个多边形由 条线段组成,那么这个多边形就叫做 边形,
是最简单的多边形。
叫做多边形的内角。
叫做多边形的外角。
叫做多边形的对角线。
(6)如果 ,那么这个多边形就是凸多边形。
(7) 叫做正多边形。
三、合作探究
1、课本81页练习1、2;
2、从六边形的一个顶点出发可以画出几条对角线?他们将六边形分成几个三角形?
七边形呢?
由此你能得出多边形对角线条数与它的变数的关系吗?
一个八边形,它有 条对角线。
四、巩固提高
课本84页习题7.3 1、
七年级下册数学 第七章 三角形
导学7 7.3.1多边形的内角和
学习目标
会计算多边形的内角和
会计算多边形的外角和
会利用内角和、外角和求多边形的边数
自主学习
1、从n边形的一个顶点可以画 条对角线,它们可以将n边形分成 个三角形?
2、阅读课本81—82页
3、n边形的内角和等于
4、做课本83页练习1(1)(2)(4)
5、做课本84页习题7.3 2、4
三、合作探究
1、课本82页例1
2、课本82页例2
3、多边形的外角和等于
4、做课本84页练习1(3)
四、巩固提高
1、一个多边形的格内角都等于120度,它是几边形?
2、一个多边形的内角和与外角和相等,它是几边形?
3、课本85页5、6题
七年级下册数学 第七章 三角形
导学 8 复习 三角形 (一)
学习目标:
理解并掌握本章有关概念及性质。
会用本章知识解决问题。
自主学习:
阅读课本第七章内容,回答下列问题:
有关概念
什么叫三角形?三角形的高、中线、角平分线?
什么叫多边形?多边形的对角线?
什么叫平面镶嵌?
有关性质:
三角形三边的关系?
三角形、多边形的内角和?外角和?
3. 三角形外角的性质?
用一种或两种正多边形进行平面镶嵌的条件是什么?
合作探究:
先独立完成下列问题,再小组交流
1. 以下列各组线段长为边能构成三角形的是( )
(A) 7. 12. 5 (B) 6. 8. 15 (C) 4. 5. 3 (D) 8. 3. 4
2. 在△ABC中,若∠C=90 ∠CAB与∠CBA的平分线相交于点O,则∠AOB=( )
(A) 105 (B)120 (C)135 (D)150
3. 如图,∠BOC=100 ∠C=20 ∠B=25 ,则∠A=( )
4. 正三角形、正四边形、正五边形、正六边形、正八边形,在选择其中一种正多边形进行平面镶嵌,可选择的是 。
巩固提高:
1. 已知:△ABC中, AD⊥BC于D,∠DAC=∠C,∠B=65
则∠BAC= 。
2. 如图,已知 ∠B=42 ∠A+10 =∠C AB∥C
则 ∠ACD=
3. 如果一个凸多边形从一个顶点引出的对角线条数为4, 则这个多边形为 边形, 内角和
是 。
4. 如图,在小河的一边开两条小渠,设计要求两条水渠成45 角,有人采取这样的方法:在两个水渠内侧各取一点E F 之后连起来,并测得∠CEF=100 ∠BFE=55 .问这条水渠是否符合要求?并说明理由。
七年级下册数学 第七章 三角形
导学9 复习三角形 专题训练 (二)
一、 学习目标:
1. 学会分析解题思路
2. 学会用本章知识解决实际问题
二、 自主学习:
专题①: 与三角形有关的线段:
三角形的高构造了 条件, 三角形的中线隐含了 相等的条件。
将三角形面积分成 两部分, 三角形的角平分线提供了
相等条件。
专题②: 三角形内角和及外角的性质
三角形内角和与外角性质为解题提供了隐含条件,可解决许多有关三角形 问题。
专题③: 多边形内角和及外角和
求多边形的内角、外角、边数及对角线问题时,常用到多边形的公式是 。
专题④: 平面镶嵌
常用的平面镶嵌大多是 的镶嵌, 主要限于用 种正多边形镶嵌和允许用 种正多边形镶嵌两种类型
三、 合作探究
1. 如图(1),在△ABC中,AD、AE分别是BC边的中线和高,AB=10, AC=6
则△ABD与△ACD的周长之差
是 面积关系是
2. 如图(2),已知△ABC中,D在BC的延长线上,E在CA的延长线上,F在AB上,则∠2 ∠1 (填“<”或“=”或“>”)
3. 已知,一个多边形内角和是外角和的2.5倍,则此多边形的边数为 。
4. 三角形最长边等于10,另外两边长分别为X和4,周长为C,则X的取值范围是 C的取值范围是 。
四、 巩固提高:
1. 如图(4),在△ABC中,AD是高,AE 是∠BAC的角平分线,∠B=20 , ∠C=60 ,求∠DAE的度数
2. 某校欲建一座足球场,现有正三角形、正六边形、正八边形、正十边形五种形状的草皮,请你帮助选择两种草皮来铺满足球场
