3.3.2 去分母 课件(共26张PPT)
文档属性
| 名称 | 3.3.2 去分母 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-25 19:49:36 | ||
图片预览








文档简介
(共26张PPT)
第2课时 去分母
人教版七年级数学上册 ·上课课件
第三章 一元一次方程
新课导入
导入课题
英国伦敦博物馆保存着一部极其珍贵的文物——纸草书.这是古代埃及人用象形文字写在一种用纸莎草压制成的草片上的著作,它于公元前1700年左右写成,至今已有三千七百多年.这部书中记载了许多有关数学的问题,其中就有如下这道著名的求未知数的问题.一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,这个数是多少?如果设这个数为x,那么你能列出方程吗?你会解这个方程吗?今天我们就一起通过这个问题继续学习一元一次方程的解法——去分母.
学习目标
【知识与技能】
会把实际问题建成数学模型,会用去分母的方法解一元一次方程.
【过程与方法】
通过列方程解决实际问题,让学生逐步建立方程思想;通过去分母解方程,让学生了解数学中的“化归”思想.
【情感态度】
让学生了解数学的渊源及辉煌的历史,激发学生的学习热情.
【教学重点】
会用去分母的方法解一元一次方程.
【教学难点】
实际问题中如何建立等量关系,并根据等量关系列出方程.
推进新课
知识点1
去分母
数学小史料
英国伦敦博物馆保存着
一部极其珍贵的文物——
纸草书.这是古代埃及人用
象形文字写在一种用纸莎草
压制成的草片上的著作,它于公元前1700年左右写成.
这部书中记载了许多有关数学的问题.
问题2
一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,求这个数.
分析:设这个数为x.
根据题意,得
方法1:合并同类项,得
系数化为1,得
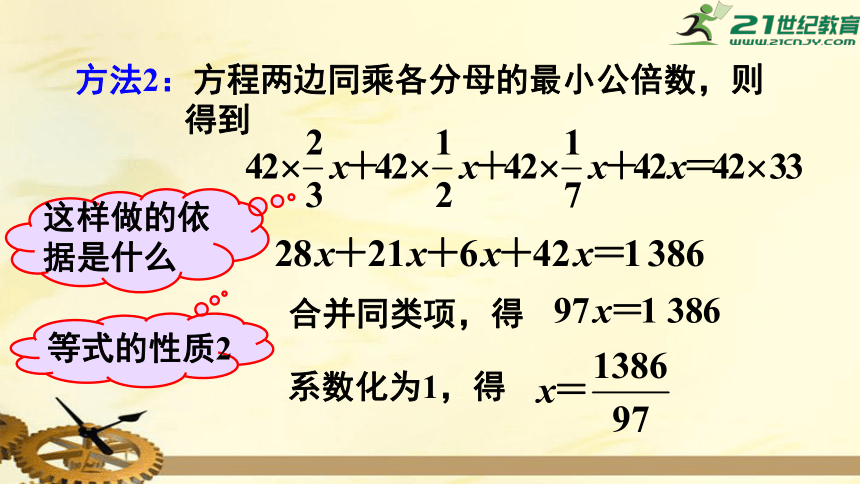
方法2:方程两边同乘各分母的最小公倍数,则
得到
合并同类项,得
系数化为1,得
这样做的依据是什么
等式的性质2
为了更全面的讨论问题,我们再以方程
为例.
方程两边乘10,
下面的框图表示解这个方程的流程.
5(3x+1)– 10×2=(3x – 2)– 2(2x+3)
15x + 5 – 20 = 3x – 2 – 4x – 6
15x – 3x + 4x = – 2 – 6 – 5+20
16x = 7
去分母(方程两边乘各分母的最小公倍数)
去括号
移项
合并同类项
系数化为1
归纳
解一元一次方程的一般步骤包括:去分母、去括号、移项、合并同类项、系数化为1等. 通过这些步骤可以使以x为未知数的方程逐步向着x=a的形式转化,这个过程主要依据等式的基本性质和运算律等.
例3 解下列方程:
解:去分母(方程两边乘4),得
2(x + 1) – 4 = 8 +(2 – x).
去括号,得 2x + 2 – 4 = 8 + 2 – x.
移项,得 2x + x = 8 + 2 – 2 + 4 .
合并同类项,得 3x = 12.
系数化为1,得 x = 4.
解:去分母(方程两边乘6),得
18x + 3(x – 1)= 18 – 2(2x – 1)
去括号,得 18x + 3x – 3 = 18 – 4x + 2
移项,得 18x + 3x +4x = 18 + 2 + 3
合并同类项,得 25x = 23
系数化为1,得
在本章第一个问题中,我们根据路程、速度和时间三者的关系列出方程
现在解这个方程
去分母(方程两边乘420),得
7x – 6x = 420
x = 420
解:去分母(方程两边乘100),得
19x = 21(x – 2).
去括号,得 19x = 21x – 42.
移项,得 19x – 21x = – 42.
合并同类项,得 – 2x = – 42.
系数化为1,得 x = 21.
练习1 解下列方程:
巩固练习
解:去分母(方程两边乘4),得
2(x + 1)– 8 = x.
去括号,得 2x + 2 – 8 = x .
移项,得 2x – x =8 – 2
合并同类项,得 x = 6.
解:去分母(方程两边乘12),得
3(5x – 1) = 6(3x + 1)– 4(2 – x)
去括号,得 15x – 3 = 18x + 6– 8 + 4x
移项,得 15x – 18x – 4x = 6 – 8 + 3
合并同类项,得 – 7x = 1
系数化为1,得
解:去分母(方程两边乘20),得
10(3x + 2)– 20 = 5(2x – 1)– 4(2x + 1)
去括号,得 30x +20 – 20 = 10x –5 – 8x – 4
移项,得 30x – 10x + 8x = – 5 – 4 – 20+20
合并同类项,得 28x = – 9
系数化为1,得
练习2 某中学组织团员到校外参加义务植树活动,一部分团员骑自行车先走,速度为 9 km/h,40分钟后其余团员乘汽车出发,速度为 45 km/h,结果他们同时到达目的地,则目的地距学校多少千米?
解:设目的地距学校x km,则骑自行车所用时间为 h,乘汽车所用时间为 h.
由题意,得 解得 x=7.5.
答:目的地距学校7.5 km.
随堂演练
基础巩固
1. 解方程 时,去分母正确的是( )
A. 3x-1 = 2(x-1)
B. 3x-6 = 2(x-1)
C. 3x-6 = 2x-1
D. 3x-3 = 2x-1
B
2. 解方程:
解:第一步________,得10 – 2(x + 2) = 5(x – 1).
第二步________,得10 –2x – 4 = 5x – 5.
第三步______,得 – 2x – 5x = –5 –10 + 4.
第四步____________,得 – 7x = –11.
第五步____________,得 x = .
去分母
去括号
移项
合并同类项
系数化为1
综合应用
3. 列方程解答下面问题. y的3倍与1.5的和的二分之一等于y与1的差的四分之一,求y.
解:根据题意,得
解得
拓展延伸
4. 有一些相同的房间需要粉刷墙面,一天3名一级技工去粉刷8个房间,结果其中有50 m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40 m2墙面,每名一级技工比二级技工一天多粉刷10 m2墙面,求每个房间需要粉刷的墙面面积.
解:设每个房间需要粉刷的墙面面积为x m2.
解得 x = 52
答:每个房间需要粉刷的墙面面积为52 m2.
则
课堂小结
归纳
解一元一次方程的一般步骤包括:去分母、去括号、移项、合并同类项、系数化为1等. 通过这些步骤可以使以x为未知数的方程逐步向着x=a的形式转化,这个过程主要依据等式的基本性质和运算律等.
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第2课时 去分母
人教版七年级数学上册 ·上课课件
第三章 一元一次方程
新课导入
导入课题
英国伦敦博物馆保存着一部极其珍贵的文物——纸草书.这是古代埃及人用象形文字写在一种用纸莎草压制成的草片上的著作,它于公元前1700年左右写成,至今已有三千七百多年.这部书中记载了许多有关数学的问题,其中就有如下这道著名的求未知数的问题.一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,这个数是多少?如果设这个数为x,那么你能列出方程吗?你会解这个方程吗?今天我们就一起通过这个问题继续学习一元一次方程的解法——去分母.
学习目标
【知识与技能】
会把实际问题建成数学模型,会用去分母的方法解一元一次方程.
【过程与方法】
通过列方程解决实际问题,让学生逐步建立方程思想;通过去分母解方程,让学生了解数学中的“化归”思想.
【情感态度】
让学生了解数学的渊源及辉煌的历史,激发学生的学习热情.
【教学重点】
会用去分母的方法解一元一次方程.
【教学难点】
实际问题中如何建立等量关系,并根据等量关系列出方程.
推进新课
知识点1
去分母
数学小史料
英国伦敦博物馆保存着
一部极其珍贵的文物——
纸草书.这是古代埃及人用
象形文字写在一种用纸莎草
压制成的草片上的著作,它于公元前1700年左右写成.
这部书中记载了许多有关数学的问题.
问题2
一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,求这个数.
分析:设这个数为x.
根据题意,得
方法1:合并同类项,得
系数化为1,得
方法2:方程两边同乘各分母的最小公倍数,则
得到
合并同类项,得
系数化为1,得
这样做的依据是什么
等式的性质2
为了更全面的讨论问题,我们再以方程
为例.
方程两边乘10,
下面的框图表示解这个方程的流程.
5(3x+1)– 10×2=(3x – 2)– 2(2x+3)
15x + 5 – 20 = 3x – 2 – 4x – 6
15x – 3x + 4x = – 2 – 6 – 5+20
16x = 7
去分母(方程两边乘各分母的最小公倍数)
去括号
移项
合并同类项
系数化为1
归纳
解一元一次方程的一般步骤包括:去分母、去括号、移项、合并同类项、系数化为1等. 通过这些步骤可以使以x为未知数的方程逐步向着x=a的形式转化,这个过程主要依据等式的基本性质和运算律等.
例3 解下列方程:
解:去分母(方程两边乘4),得
2(x + 1) – 4 = 8 +(2 – x).
去括号,得 2x + 2 – 4 = 8 + 2 – x.
移项,得 2x + x = 8 + 2 – 2 + 4 .
合并同类项,得 3x = 12.
系数化为1,得 x = 4.
解:去分母(方程两边乘6),得
18x + 3(x – 1)= 18 – 2(2x – 1)
去括号,得 18x + 3x – 3 = 18 – 4x + 2
移项,得 18x + 3x +4x = 18 + 2 + 3
合并同类项,得 25x = 23
系数化为1,得
在本章第一个问题中,我们根据路程、速度和时间三者的关系列出方程
现在解这个方程
去分母(方程两边乘420),得
7x – 6x = 420
x = 420
解:去分母(方程两边乘100),得
19x = 21(x – 2).
去括号,得 19x = 21x – 42.
移项,得 19x – 21x = – 42.
合并同类项,得 – 2x = – 42.
系数化为1,得 x = 21.
练习1 解下列方程:
巩固练习
解:去分母(方程两边乘4),得
2(x + 1)– 8 = x.
去括号,得 2x + 2 – 8 = x .
移项,得 2x – x =8 – 2
合并同类项,得 x = 6.
解:去分母(方程两边乘12),得
3(5x – 1) = 6(3x + 1)– 4(2 – x)
去括号,得 15x – 3 = 18x + 6– 8 + 4x
移项,得 15x – 18x – 4x = 6 – 8 + 3
合并同类项,得 – 7x = 1
系数化为1,得
解:去分母(方程两边乘20),得
10(3x + 2)– 20 = 5(2x – 1)– 4(2x + 1)
去括号,得 30x +20 – 20 = 10x –5 – 8x – 4
移项,得 30x – 10x + 8x = – 5 – 4 – 20+20
合并同类项,得 28x = – 9
系数化为1,得
练习2 某中学组织团员到校外参加义务植树活动,一部分团员骑自行车先走,速度为 9 km/h,40分钟后其余团员乘汽车出发,速度为 45 km/h,结果他们同时到达目的地,则目的地距学校多少千米?
解:设目的地距学校x km,则骑自行车所用时间为 h,乘汽车所用时间为 h.
由题意,得 解得 x=7.5.
答:目的地距学校7.5 km.
随堂演练
基础巩固
1. 解方程 时,去分母正确的是( )
A. 3x-1 = 2(x-1)
B. 3x-6 = 2(x-1)
C. 3x-6 = 2x-1
D. 3x-3 = 2x-1
B
2. 解方程:
解:第一步________,得10 – 2(x + 2) = 5(x – 1).
第二步________,得10 –2x – 4 = 5x – 5.
第三步______,得 – 2x – 5x = –5 –10 + 4.
第四步____________,得 – 7x = –11.
第五步____________,得 x = .
去分母
去括号
移项
合并同类项
系数化为1
综合应用
3. 列方程解答下面问题. y的3倍与1.5的和的二分之一等于y与1的差的四分之一,求y.
解:根据题意,得
解得
拓展延伸
4. 有一些相同的房间需要粉刷墙面,一天3名一级技工去粉刷8个房间,结果其中有50 m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40 m2墙面,每名一级技工比二级技工一天多粉刷10 m2墙面,求每个房间需要粉刷的墙面面积.
解:设每个房间需要粉刷的墙面面积为x m2.
解得 x = 52
答:每个房间需要粉刷的墙面面积为52 m2.
则
课堂小结
归纳
解一元一次方程的一般步骤包括:去分母、去括号、移项、合并同类项、系数化为1等. 通过这些步骤可以使以x为未知数的方程逐步向着x=a的形式转化,这个过程主要依据等式的基本性质和运算律等.
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
