2021—2022学年北师大版数学九年级上册第3章 概率的进一步认识 复习课件(共17张PPT)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级上册第3章 概率的进一步认识 复习课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 990.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-24 08:39:24 | ||
图片预览




文档简介
(共17张PPT)
第三章 概率的进一步认识
概率的进一步认识
回顾与思考
复习目标
1. 建立概率知识框架图,掌握利用画树状图、列表求概率。(重点)
2.进一步理解试验频率和概率的关系,发展学生的随机观念和数据分析观念,会用所学概率知识解决实际
问题。(难点)
3. 形成一定的解决问题的策略,进一步发展学生
合作交流的能力,培养探索和创新精神。
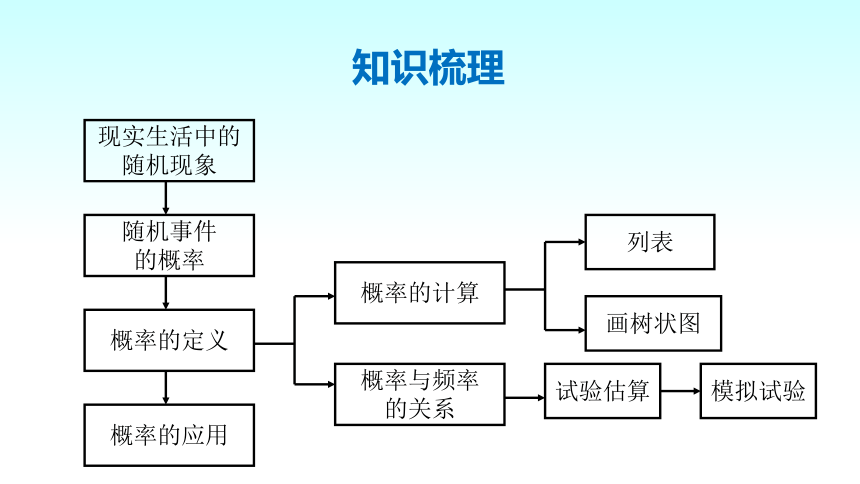
知识梳理
现实生活中的
随机现象
随机事件
的概率
概率的定义
概率的应用
概率的定义
概率的计算
概率与频率
的关系
试验估算
列表
画树状图
模拟试验
专题一 用树状图或列表求随机事件的概率
例1:小明、小颖做一个“配色”游戏。如图,两个自由转动
的转盘,每个转盘被分成面积相等的几个扇形。同时转动两个
转盘,如果转盘A转出红色,转盘B转出蓝色,或者转盘A转
出蓝色,转盘B转出红色,红色加蓝色配成了紫色,则小颖
获胜;同样,蓝色和黄色配成了绿色,则小明获胜;在
其他情况下则小明小颖
不分胜负。
小颖
小明
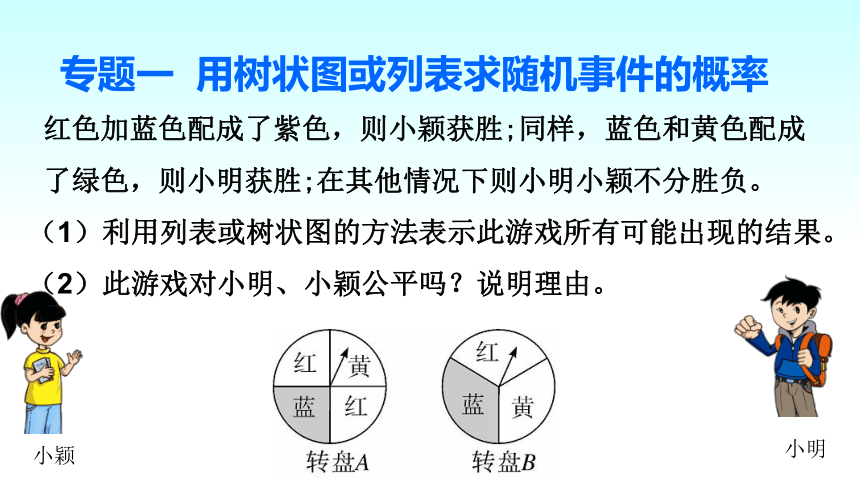
专题一 用树状图或列表求随机事件的概率
红色加蓝色配成了紫色,则小颖获胜;同样,蓝色和黄色配成
了绿色,则小明获胜;在其他情况下则小明小颖不分胜负。
(1)利用列表或树状图的方法表示此游戏所有可能出现的结果。
(2)此游戏对小明、小颖公平吗?说明理由。
小颖
小明
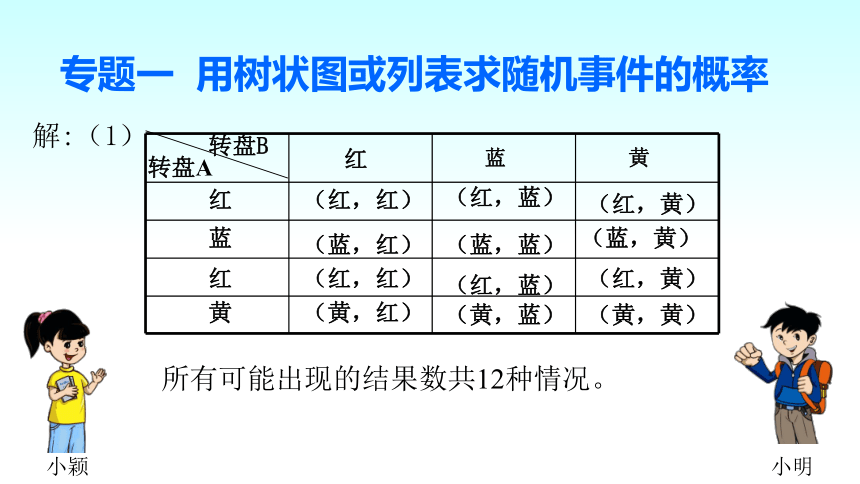
专题一 用树状图或列表求随机事件的概率
解:(1)
小颖
小明
转盘A
转盘B
红
蓝
黄
红
蓝
红
黄
(红,红)
(红,红)
(黄,红)
(蓝,红)
(黄,黄)
(蓝,蓝)
(红,蓝)
(黄,蓝)
(红,黄)
(蓝,黄)
(红,黄)
(红,蓝)
所有可能出现的结果数共12种情况。
专题一 用树状图或列表求随机事件的概率
(2)不公平
P(小颖获胜)=
P(小明获胜)=
此游戏对小明、小颖不公平。
小颖
小明
在对概率知识进行考查时,出现了许多判断游戏公平与否的问题,解决这类问题的一般方法是先求其概率,然后通过比较概率的大小来判断游戏的公平性。
方法总结:
专题一 用树状图或列表求随机事件的概率
例2:如图,将一枚棋子依次沿正方形ABCD四个顶点A,B,
C,D,A,B,C……移动。开始时,棋子位于点A处;然后,根据
掷骰子掷得的点数移动棋子(如掷得1点就移动1步到点B处,
如掷得6点就移动6步到点C处……)以移动后棋子所在的位置
为新起点,再进行同样的操作。在第二次掷骰子
后,棋子回到点A处的概率是多少?
A
B
C
D
问题:第二次掷得骰子后,棋子回到点A处的概率是多少?
A
B
C
D
专题一 用树状图或列表求随机事件的概率
解:P(棋子回到点A处)= =
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
第一次
第二次
专题二 用频率估计概率
例3:在一个不透明的盒子里装了只有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里的球搅匀后从中随机摸出一个球,记下颜色再把它放回盒子里,不断重复上述过程。下表是试验中的一组统计数据:
专题二 用频率估计概率
(1)请估计:当n很大时,摸到白球的频率是多少?
(2)假如你摸一次,估计摸到白球的概率P是多少?
(3)试估计盒子里黑、白两种颜色的球各有多少个?
摸球的
次数 100 200 300 500 800 1000 3000
摸到白球的次数 65 124 178 302 481 599 1803
摸到白球的频率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
专题二 用频率估计概率
(1)请估计:当n很大时,摸到白球的频率是多少?
(2)假如你摸一次,估计摸到白球的概率P是多少?
(3)试估计盒子里黑、白两种颜色的球各有多少个?
解:(1)白球的频率是0.6
(2)P(摸到白球)=0.6
(3)40 0.6=24(个) 40—24=16(个)
盒子里白球有24个,黑球有16个。
总结提升:
1.通过本节课的学习,你获得了哪些知识、方法?
你认为这节课的重点是什么?
2.所学知识能解决哪些实际问题?
3.本节课所运用的学习方法对你今后有什么启示?
方法总结:
用树状图或列表分析是计算等可能事件概率的常用方法(1)当事件要经过两步完成时,特别是三步及以上完成的试验,用画树状图分析很有效,(2)一次试验要涉及两步,并且可能出现的结果数目较多时,通常采用列表法分析所有等可的结果。当结果要求进行数的和、
积等有关运算时,用列表显得更加清晰、明确。
再 见
第三章 概率的进一步认识
概率的进一步认识
回顾与思考
复习目标
1. 建立概率知识框架图,掌握利用画树状图、列表求概率。(重点)
2.进一步理解试验频率和概率的关系,发展学生的随机观念和数据分析观念,会用所学概率知识解决实际
问题。(难点)
3. 形成一定的解决问题的策略,进一步发展学生
合作交流的能力,培养探索和创新精神。
知识梳理
现实生活中的
随机现象
随机事件
的概率
概率的定义
概率的应用
概率的定义
概率的计算
概率与频率
的关系
试验估算
列表
画树状图
模拟试验
专题一 用树状图或列表求随机事件的概率
例1:小明、小颖做一个“配色”游戏。如图,两个自由转动
的转盘,每个转盘被分成面积相等的几个扇形。同时转动两个
转盘,如果转盘A转出红色,转盘B转出蓝色,或者转盘A转
出蓝色,转盘B转出红色,红色加蓝色配成了紫色,则小颖
获胜;同样,蓝色和黄色配成了绿色,则小明获胜;在
其他情况下则小明小颖
不分胜负。
小颖
小明
专题一 用树状图或列表求随机事件的概率
红色加蓝色配成了紫色,则小颖获胜;同样,蓝色和黄色配成
了绿色,则小明获胜;在其他情况下则小明小颖不分胜负。
(1)利用列表或树状图的方法表示此游戏所有可能出现的结果。
(2)此游戏对小明、小颖公平吗?说明理由。
小颖
小明
专题一 用树状图或列表求随机事件的概率
解:(1)
小颖
小明
转盘A
转盘B
红
蓝
黄
红
蓝
红
黄
(红,红)
(红,红)
(黄,红)
(蓝,红)
(黄,黄)
(蓝,蓝)
(红,蓝)
(黄,蓝)
(红,黄)
(蓝,黄)
(红,黄)
(红,蓝)
所有可能出现的结果数共12种情况。
专题一 用树状图或列表求随机事件的概率
(2)不公平
P(小颖获胜)=
P(小明获胜)=
此游戏对小明、小颖不公平。
小颖
小明
在对概率知识进行考查时,出现了许多判断游戏公平与否的问题,解决这类问题的一般方法是先求其概率,然后通过比较概率的大小来判断游戏的公平性。
方法总结:
专题一 用树状图或列表求随机事件的概率
例2:如图,将一枚棋子依次沿正方形ABCD四个顶点A,B,
C,D,A,B,C……移动。开始时,棋子位于点A处;然后,根据
掷骰子掷得的点数移动棋子(如掷得1点就移动1步到点B处,
如掷得6点就移动6步到点C处……)以移动后棋子所在的位置
为新起点,再进行同样的操作。在第二次掷骰子
后,棋子回到点A处的概率是多少?
A
B
C
D
问题:第二次掷得骰子后,棋子回到点A处的概率是多少?
A
B
C
D
专题一 用树状图或列表求随机事件的概率
解:P(棋子回到点A处)= =
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
第一次
第二次
专题二 用频率估计概率
例3:在一个不透明的盒子里装了只有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里的球搅匀后从中随机摸出一个球,记下颜色再把它放回盒子里,不断重复上述过程。下表是试验中的一组统计数据:
专题二 用频率估计概率
(1)请估计:当n很大时,摸到白球的频率是多少?
(2)假如你摸一次,估计摸到白球的概率P是多少?
(3)试估计盒子里黑、白两种颜色的球各有多少个?
摸球的
次数 100 200 300 500 800 1000 3000
摸到白球的次数 65 124 178 302 481 599 1803
摸到白球的频率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
专题二 用频率估计概率
(1)请估计:当n很大时,摸到白球的频率是多少?
(2)假如你摸一次,估计摸到白球的概率P是多少?
(3)试估计盒子里黑、白两种颜色的球各有多少个?
解:(1)白球的频率是0.6
(2)P(摸到白球)=0.6
(3)40 0.6=24(个) 40—24=16(个)
盒子里白球有24个,黑球有16个。
总结提升:
1.通过本节课的学习,你获得了哪些知识、方法?
你认为这节课的重点是什么?
2.所学知识能解决哪些实际问题?
3.本节课所运用的学习方法对你今后有什么启示?
方法总结:
用树状图或列表分析是计算等可能事件概率的常用方法(1)当事件要经过两步完成时,特别是三步及以上完成的试验,用画树状图分析很有效,(2)一次试验要涉及两步,并且可能出现的结果数目较多时,通常采用列表法分析所有等可的结果。当结果要求进行数的和、
积等有关运算时,用列表显得更加清晰、明确。
再 见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
