人教版六年级上册数学4.1比的意义讲解视频+课本习题讲解+考点+PPT课件【易懂通课堂】
文档属性
| 名称 | 人教版六年级上册数学4.1比的意义讲解视频+课本习题讲解+考点+PPT课件【易懂通课堂】 |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-24 10:28:08 | ||
图片预览








文档简介
(共33张PPT)
4.1 比的意义
人教版六年级上册
易懂通课堂(用最简洁的方法让学生听懂重难点)
讲解设计:立足课本
1.基础部分
2.核心讲解
3.基础考点
4.核心考点
5.后面大量练习,先暂停页面,做完后听讲解核对。
比
4
后面精彩片段截屏
2003年10月15日,我国第一艘载人飞船“神舟”五号顺利升空,在太空中执行此次任务的航天员杨利伟在飞船里向人们展示了联合国国旗和中华人民共和国国旗。
3
一
基础部分
2003年10月15日,我国第一艘载人飞船“神舟”五号顺利升空,在太空中执行此次任务的航天员杨利伟在飞船里向人们展示了联合国国旗和中华人民共和国国旗。
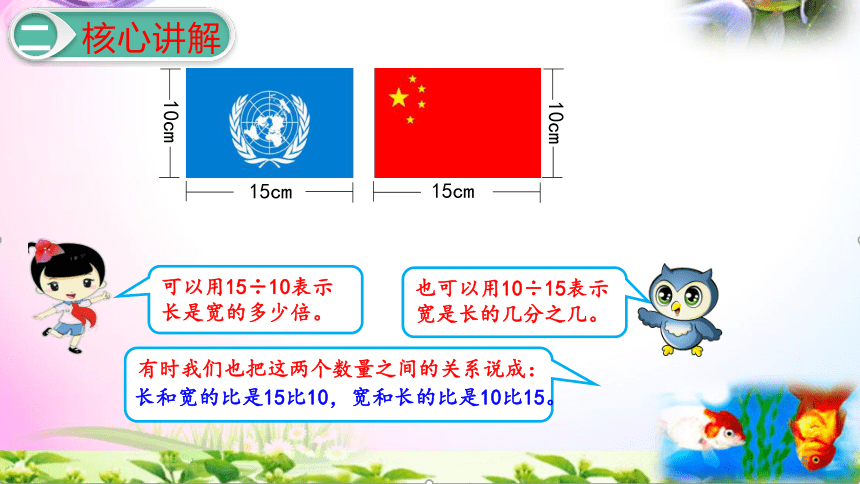
杨利伟展示的两面旗都是长15cm,宽10cm。怎样用算式表示它们长和宽的倍数关系?
4
二
核心讲解
15cm
15cm
10cm
10cm
也可以用10÷15表示宽是长的几分之几。
可以用15÷10表示长是宽的多少倍。
有时我们也把这两个数量之间的关系说成:
长和宽的比是15比10,宽和长的比是10比15。
5
二
核心讲解
时间
路程
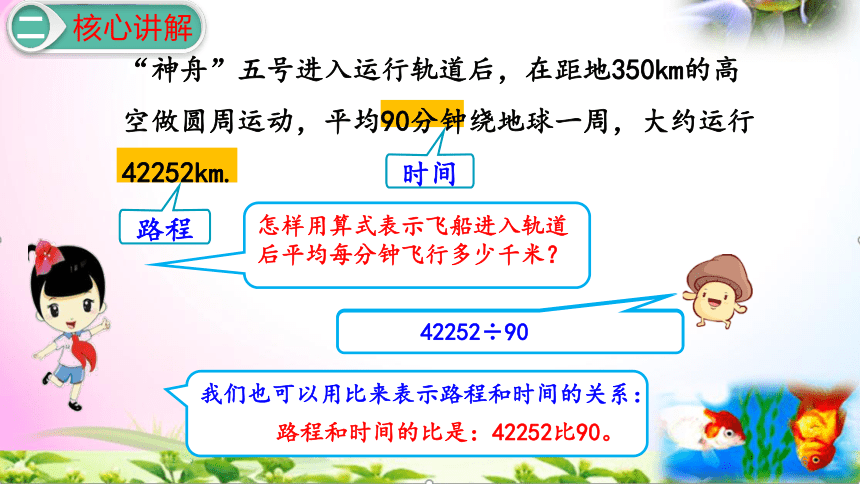
怎样用算式表示飞船进入轨道后平均每分钟飞行多少千米?
速度可以用路程÷时间表示。
我们也可以用比来表示路程和时间的关系:
路程和时间的比是:42252比90。
42252÷90
“神舟”五号进入运行轨道后,在距地350km的高空做圆周运动,平均90分钟绕地球一周,大约运行42252km.
6
二
核心讲解
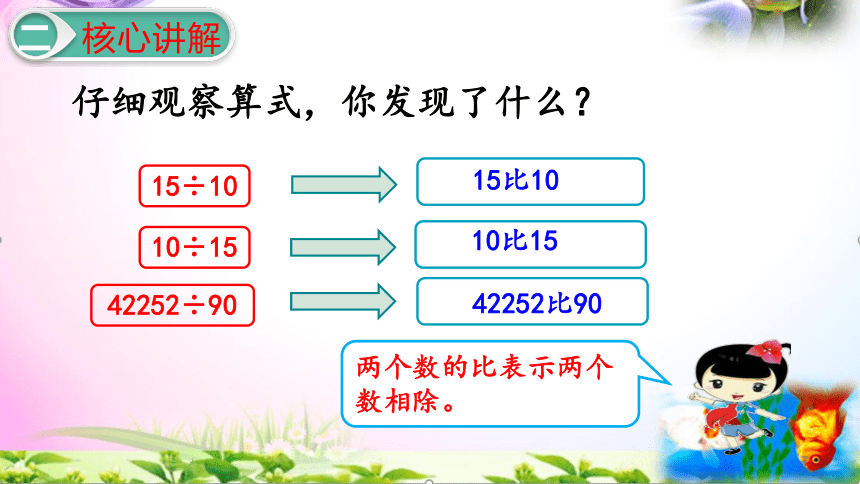
仔细观察算式,你发现了什么?
15÷10
10÷15
42252÷90
15比10
10比15
42252比90
两个数的比表示两个数相除。
7
二
核心讲解
15比10记作15:10
10比15记作
42252比90记作
“:”是比号,读作“比”。
在两个数的比中,比号前面的数叫做比的 ,
15
10
:
15
10
=
÷
=
前项
比号
后项
比值
比值通常用分数表示,能除尽时也可以用小数表示,能整除时要用整数表示。
10:15
42252:90
比号后面的数叫做比的后项。
比的前项除以后项所得的商,叫做比值。
前项
8
二
核心讲解
(除数)
(被除数)
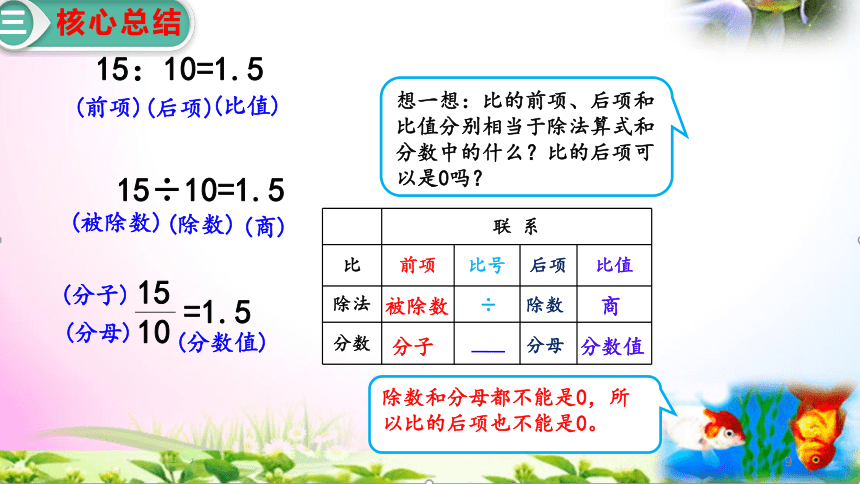
15:10=1.5
15÷10=1.5
=1.5
15
10
(前项)
(后项)
(比值)
(分母)
(商)
(被除数)
(除数)
(分子)
(分数值)
想一想:比的前项、后项和比值分别相当于除法算式和分数中的什么?比的后项可以是0吗?
联 系
比 前项 比号 后项 比值
除法
分数
被除数
÷
商
除数
分子
分母
分数值
除数和分母都不能是0,所以比的后项也不能是0。
9
三
核心总结
1.小敏和小亮在文具店买同样的练习本。小敏
买了6本,共花了1.8元。小亮买了8本,共
花了2.4元。小敏和小亮买的练习本数之比
是( )∶( ),比值是( ) ;花的钱
数之比是( ):( ),比值是( ) 。
6
8
1.8
2.4
四
基础考题
2. 3∶ ( ) =24
( ) ∶8=0.5
4
四
基础考题
我们航海模型小组男
生有14人,女生有8人。
我们航空模型小组共有26人,其中男生有16人。
我们汽车模型小组共有12人,共做了18个汽车模型。
4.
四
基础考题
(1)航海模型小组男女生人数的比是( ),
比值是( )。
7
4
(2)航空模型小组男女生人数的比是( ),
比值是( )。女生人数与小组总人数的
比是( )比值是( )
8
5
5
13
14:8
16:10
10:26
四
基础考题
(3)汽车模型小组做的模型总数与人数的
比是( ),比值是( )。
3
2
18:12
四
基础考题
5.六年级(5)班有男生20人,女生18人,求下列各比。
(1) 男生人数∶女生人数;
(2) 女生人数∶全班人数;
(3) 男生人数∶全班人数。
(1) 10 ∶9 (2)9∶19 (3) 10 ∶19
四
基础考题
欢欢花的时间是乐乐的 欢欢和乐乐所用的时间比是2:3;
2
3
6.欢欢和乐乐分别从各自的家去游乐场,欢欢走的
路程是乐乐的 ,而欢欢花的时间是乐乐的 ,
欢欢和乐乐的速度比是多少?
8
9
2
3
思路引导:
欢欢走的路程是乐乐的 欢欢和乐乐所走的路程比是8:9;
8
9
考点1
(8÷2):(9÷3)=4:3
答:欢欢和乐乐的速度比是4:3。
根据“路程÷时间=速度”可以得到欢欢和乐乐的速度比是(8÷2):(9÷3)。
6.欢欢和乐乐分别从各自的家去游乐场,欢欢走的
路程是乐乐的 ,而欢欢花的时间是乐乐的 ,
欢欢和乐乐的速度比是多少?
8
9
2
3
考点1
15 ∶ 10 = 15 ÷ 10 =
3
2
……
前
项
……
比号
……
后项
……
比值
两个数的比表示两个数相除。
两个数的比也可以写成分数形式。
比值通常用分数表示,也可以用小数或整数表示。
四
核心总结
1.填一填。
(1)下面队旗的长是80厘米,宽是60厘米,宽是长的 ,长与宽的比是( )∶( )。
(2)15∶16读作( ),还可以写成( )。
(3)两个数( )又叫做两个数的( )。
(4)如果x∶y=k,那么x叫做比的( ),y叫做比的( ),k叫做( )。
4
3
80
60
15比16
相除
比
前项
后项
比值
考点2
2.填一填。
(1)甲数是20,乙数是25,甲数与乙数的比是( )∶( ),比值是( )。
(2)一个比的前项是1.2,比值是,后项是( )。
20
25
0.8
6
考点3
3. 求比值。
40
4.9
6∶18
0.4∶0.01
考点4
4.一辆小汽车4小时行了340千米,所行的路程与时间的比是多少?比值是多少?这个比值表示的实际意义是什么?
340:4
85
小汽车的速度
考点4
7.判断
(1)分数既可以看作分数,也可以看作比。( )
(2)因为除数相当于比的后项,所以比的后项不能是0。( )
(3)a÷b=6,a与b的比是6∶1。( )
考点5
7*.甲数和乙数的比是2∶3,乙数和丙数的比是4∶5。甲数和丙数的比是多少?
甲数和丙数的比是8∶15。
考点6
8∶12
12∶15
14.两辆自行车的速度比是3∶2,行驶的时间比是4∶5,那么两辆自行车行驶的路程比是多少?
(3×4)∶(2×5)=12∶10
答:两辆自行车行驶的路程比是12∶10
考点7
12.想一想,填一填。
(1)甲比乙多 ,则甲5和乙4的比是( )∶( )。
(2)甲比乙少 ,则甲和乙的比是( )∶( )。
(3)六(1)班女生人数是男生的 ,男生人数与女生人数的比是( )∶( ),女生人数与全班人数的比是( ):( )。
5
4
3
4
5
8
5
13
考点8
在下面的括号里填上合适的数。
8∶( )=12 ( )∶9=0.5
27
考点9
根据比和除法的关系,可以推导出:比的前项=比的后项×比值,比的后项=比的前项÷比值。第一小题求的是比的后项:8÷12=,第二小题求的是比的前项:9×0.5=4.5。
8∶( )=12 ( 4.5 )∶9=0.5
两个服装厂一个月内生产的西服数量的比是6∶5,两个服装厂西服的单价比是11∶10。这两个服装厂的总产值之比是多少
28
因为“西服的总产值=西服的单价×数量”,所以两个服装厂总产值的比等于西服的单价乘数量的积的比。
(11×6)∶(10×5)=66∶50
答:这两个服装厂的总产值之比是66∶50。
考点9
买3千克苹果用了7元。
买苹果的总价和数量的比是( ),比值是( )。
7:3
7
3
29
考点10
判断题
小强的身高1米,他爸爸的身高是173厘米,小强说他和他爸爸的身高比是1 ︰173,对不对?如果不对,你认为是多少呢?
100︰ 173
1︰ 1.73
30
考点11
填空。
我校六年级(2)班有男生31人,女生23人。
(1)男生人数与女生人数的比是( ),比值是( )。
(2)女生人数与男生人数的比是( ),比值是( )。
(3)女生人数与全班人数的比是( ),比值是( )。
(4)全班人数与女生人数的比是( ),比值是( )。
31︰ 23
23︰31
23︰54
54 ︰23
31
考点12
判断。
1.比的前、后项可以是任意数。( )
2.5米比7米的比值是5:7。 ( )
3.一场球赛的比分是2:0,因此比的后项可以是0。( )
4.3:6比值是2。 ( )
5.明明身高是1米,爸爸身高是178厘米,明明和爸爸的身高比是1 :178 。 ( )
×
×
√
×
×
32
考点12
4.1 比的意义
人教版六年级上册
易懂通课堂(用最简洁的方法让学生听懂重难点)
讲解设计:立足课本
1.基础部分
2.核心讲解
3.基础考点
4.核心考点
5.后面大量练习,先暂停页面,做完后听讲解核对。
比
4
后面精彩片段截屏
2003年10月15日,我国第一艘载人飞船“神舟”五号顺利升空,在太空中执行此次任务的航天员杨利伟在飞船里向人们展示了联合国国旗和中华人民共和国国旗。
3
一
基础部分
2003年10月15日,我国第一艘载人飞船“神舟”五号顺利升空,在太空中执行此次任务的航天员杨利伟在飞船里向人们展示了联合国国旗和中华人民共和国国旗。
杨利伟展示的两面旗都是长15cm,宽10cm。怎样用算式表示它们长和宽的倍数关系?
4
二
核心讲解
15cm
15cm
10cm
10cm
也可以用10÷15表示宽是长的几分之几。
可以用15÷10表示长是宽的多少倍。
有时我们也把这两个数量之间的关系说成:
长和宽的比是15比10,宽和长的比是10比15。
5
二
核心讲解
时间
路程
怎样用算式表示飞船进入轨道后平均每分钟飞行多少千米?
速度可以用路程÷时间表示。
我们也可以用比来表示路程和时间的关系:
路程和时间的比是:42252比90。
42252÷90
“神舟”五号进入运行轨道后,在距地350km的高空做圆周运动,平均90分钟绕地球一周,大约运行42252km.
6
二
核心讲解
仔细观察算式,你发现了什么?
15÷10
10÷15
42252÷90
15比10
10比15
42252比90
两个数的比表示两个数相除。
7
二
核心讲解
15比10记作15:10
10比15记作
42252比90记作
“:”是比号,读作“比”。
在两个数的比中,比号前面的数叫做比的 ,
15
10
:
15
10
=
÷
=
前项
比号
后项
比值
比值通常用分数表示,能除尽时也可以用小数表示,能整除时要用整数表示。
10:15
42252:90
比号后面的数叫做比的后项。
比的前项除以后项所得的商,叫做比值。
前项
8
二
核心讲解
(除数)
(被除数)
15:10=1.5
15÷10=1.5
=1.5
15
10
(前项)
(后项)
(比值)
(分母)
(商)
(被除数)
(除数)
(分子)
(分数值)
想一想:比的前项、后项和比值分别相当于除法算式和分数中的什么?比的后项可以是0吗?
联 系
比 前项 比号 后项 比值
除法
分数
被除数
÷
商
除数
分子
分母
分数值
除数和分母都不能是0,所以比的后项也不能是0。
9
三
核心总结
1.小敏和小亮在文具店买同样的练习本。小敏
买了6本,共花了1.8元。小亮买了8本,共
花了2.4元。小敏和小亮买的练习本数之比
是( )∶( ),比值是( ) ;花的钱
数之比是( ):( ),比值是( ) 。
6
8
1.8
2.4
四
基础考题
2. 3∶ ( ) =24
( ) ∶8=0.5
4
四
基础考题
我们航海模型小组男
生有14人,女生有8人。
我们航空模型小组共有26人,其中男生有16人。
我们汽车模型小组共有12人,共做了18个汽车模型。
4.
四
基础考题
(1)航海模型小组男女生人数的比是( ),
比值是( )。
7
4
(2)航空模型小组男女生人数的比是( ),
比值是( )。女生人数与小组总人数的
比是( )比值是( )
8
5
5
13
14:8
16:10
10:26
四
基础考题
(3)汽车模型小组做的模型总数与人数的
比是( ),比值是( )。
3
2
18:12
四
基础考题
5.六年级(5)班有男生20人,女生18人,求下列各比。
(1) 男生人数∶女生人数;
(2) 女生人数∶全班人数;
(3) 男生人数∶全班人数。
(1) 10 ∶9 (2)9∶19 (3) 10 ∶19
四
基础考题
欢欢花的时间是乐乐的 欢欢和乐乐所用的时间比是2:3;
2
3
6.欢欢和乐乐分别从各自的家去游乐场,欢欢走的
路程是乐乐的 ,而欢欢花的时间是乐乐的 ,
欢欢和乐乐的速度比是多少?
8
9
2
3
思路引导:
欢欢走的路程是乐乐的 欢欢和乐乐所走的路程比是8:9;
8
9
考点1
(8÷2):(9÷3)=4:3
答:欢欢和乐乐的速度比是4:3。
根据“路程÷时间=速度”可以得到欢欢和乐乐的速度比是(8÷2):(9÷3)。
6.欢欢和乐乐分别从各自的家去游乐场,欢欢走的
路程是乐乐的 ,而欢欢花的时间是乐乐的 ,
欢欢和乐乐的速度比是多少?
8
9
2
3
考点1
15 ∶ 10 = 15 ÷ 10 =
3
2
……
前
项
……
比号
……
后项
……
比值
两个数的比表示两个数相除。
两个数的比也可以写成分数形式。
比值通常用分数表示,也可以用小数或整数表示。
四
核心总结
1.填一填。
(1)下面队旗的长是80厘米,宽是60厘米,宽是长的 ,长与宽的比是( )∶( )。
(2)15∶16读作( ),还可以写成( )。
(3)两个数( )又叫做两个数的( )。
(4)如果x∶y=k,那么x叫做比的( ),y叫做比的( ),k叫做( )。
4
3
80
60
15比16
相除
比
前项
后项
比值
考点2
2.填一填。
(1)甲数是20,乙数是25,甲数与乙数的比是( )∶( ),比值是( )。
(2)一个比的前项是1.2,比值是,后项是( )。
20
25
0.8
6
考点3
3. 求比值。
40
4.9
6∶18
0.4∶0.01
考点4
4.一辆小汽车4小时行了340千米,所行的路程与时间的比是多少?比值是多少?这个比值表示的实际意义是什么?
340:4
85
小汽车的速度
考点4
7.判断
(1)分数既可以看作分数,也可以看作比。( )
(2)因为除数相当于比的后项,所以比的后项不能是0。( )
(3)a÷b=6,a与b的比是6∶1。( )
考点5
7*.甲数和乙数的比是2∶3,乙数和丙数的比是4∶5。甲数和丙数的比是多少?
甲数和丙数的比是8∶15。
考点6
8∶12
12∶15
14.两辆自行车的速度比是3∶2,行驶的时间比是4∶5,那么两辆自行车行驶的路程比是多少?
(3×4)∶(2×5)=12∶10
答:两辆自行车行驶的路程比是12∶10
考点7
12.想一想,填一填。
(1)甲比乙多 ,则甲5和乙4的比是( )∶( )。
(2)甲比乙少 ,则甲和乙的比是( )∶( )。
(3)六(1)班女生人数是男生的 ,男生人数与女生人数的比是( )∶( ),女生人数与全班人数的比是( ):( )。
5
4
3
4
5
8
5
13
考点8
在下面的括号里填上合适的数。
8∶( )=12 ( )∶9=0.5
27
考点9
根据比和除法的关系,可以推导出:比的前项=比的后项×比值,比的后项=比的前项÷比值。第一小题求的是比的后项:8÷12=,第二小题求的是比的前项:9×0.5=4.5。
8∶( )=12 ( 4.5 )∶9=0.5
两个服装厂一个月内生产的西服数量的比是6∶5,两个服装厂西服的单价比是11∶10。这两个服装厂的总产值之比是多少
28
因为“西服的总产值=西服的单价×数量”,所以两个服装厂总产值的比等于西服的单价乘数量的积的比。
(11×6)∶(10×5)=66∶50
答:这两个服装厂的总产值之比是66∶50。
考点9
买3千克苹果用了7元。
买苹果的总价和数量的比是( ),比值是( )。
7:3
7
3
29
考点10
判断题
小强的身高1米,他爸爸的身高是173厘米,小强说他和他爸爸的身高比是1 ︰173,对不对?如果不对,你认为是多少呢?
100︰ 173
1︰ 1.73
30
考点11
填空。
我校六年级(2)班有男生31人,女生23人。
(1)男生人数与女生人数的比是( ),比值是( )。
(2)女生人数与男生人数的比是( ),比值是( )。
(3)女生人数与全班人数的比是( ),比值是( )。
(4)全班人数与女生人数的比是( ),比值是( )。
31︰ 23
23︰31
23︰54
54 ︰23
31
考点12
判断。
1.比的前、后项可以是任意数。( )
2.5米比7米的比值是5:7。 ( )
3.一场球赛的比分是2:0,因此比的后项可以是0。( )
4.3:6比值是2。 ( )
5.明明身高是1米,爸爸身高是178厘米,明明和爸爸的身高比是1 :178 。 ( )
×
×
√
×
×
32
考点12
