人教版六年级上册数学5.5圆的面积(2)讲解视频+课本习题讲解+考点+PPT课件【易懂通课堂】
文档属性
| 名称 | 人教版六年级上册数学5.5圆的面积(2)讲解视频+课本习题讲解+考点+PPT课件【易懂通课堂】 |

|
|
| 格式 | zip | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-24 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
5.5 圆的面积(2)
人教版六年级上册
易懂通课堂(用最简洁的方法让学生听懂重难点)
讲解设计:立足课本
1.基础部分
2.核心讲解
3.基础考点
4.核心考点
5.后面大量练习,先暂停页面,做完后听讲解核对。
圆
5
后面精彩片段截屏
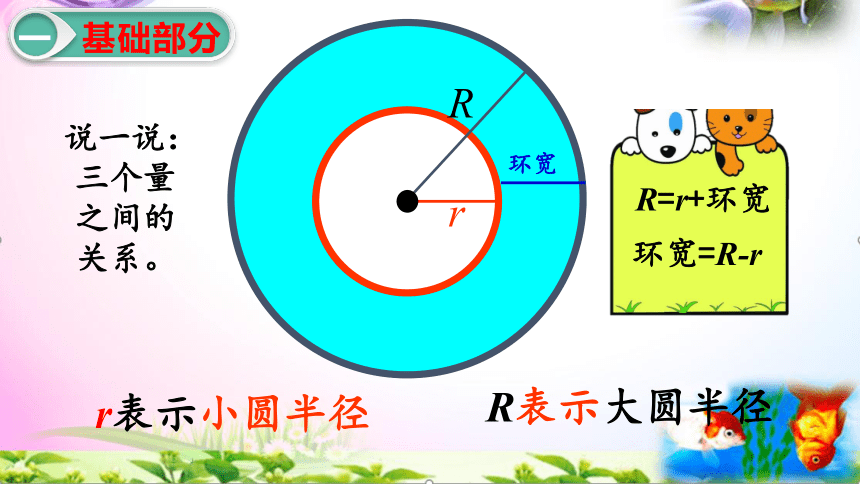
什么叫圆环?
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
知识点1:求圆环的面积
一
基础部分
一个环形具有哪些特点?
(1)它们的圆心都在同一个点上(同心圆)。
(2)两个圆间的距离处处相等。
一
基础部分
·
r
R
r表示小圆半径
R表示大圆半径
环宽
说一说:
三个量之间的关系。
R=r+环宽
环宽=R-r
一
基础部分
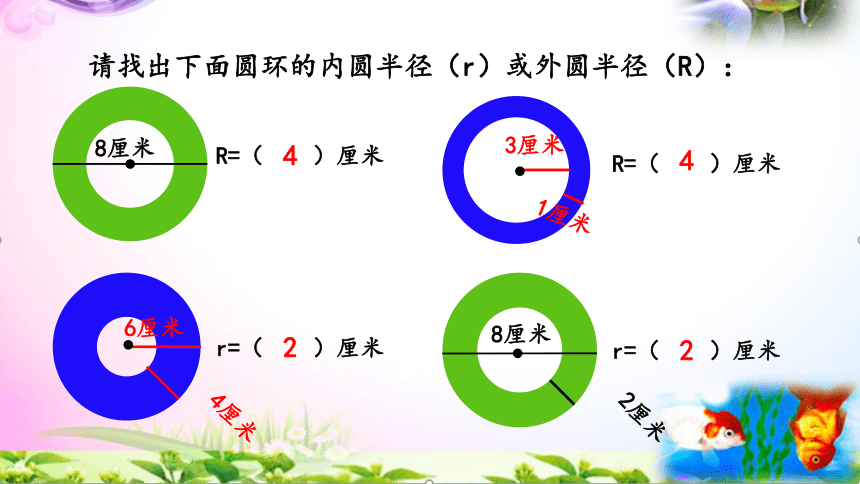
请找出下面圆环的内圆半径(r)或外圆半径(R):
8厘米
R=( )厘米
8厘米
2厘米
r=( )厘米
6厘米
4厘米
r=( )厘米
3厘米
1厘米
R=( )厘米
4
2
2
4
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
2
怎样利用内圆和外圆的面积求出圆环的面积?
一
核心讲解
2cm
6cm
3.14×6 -3.14×2
=3.14×36-3.14×4
=113.04-12.56
=100.48(平方厘米)
方法一:
答:它的面积是100.48平方厘米。
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。它的面积是多少?
(1)S环=πR2-πr2
2cm
6cm
=3.14×(36-4)
=3.14×32
3.14×(6 -2 )
方法二:
答:它的面积是100.48平方厘米。
=100.48(平方厘米)
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。它的面积是多少?
(2)S环=π×(R大2-r小2)
(1)S环=πR2-πr2
(2)S环=π×(R大2-r小2)
圆环的面积
2cm
6cm
3.14×6 -3.14×2
方法一:
3.14×(6 -2 )
方法二:
三
核心总结
圆环面积=外圆面积-内圆面积
50÷2=25(m) 10÷2=5(m)
答:草坪的占地面积是1884m 。
一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
3.14×(25 -5 )
=3.14×600
=1884(m )
4
基础考题
2.下图是一块玉璧,外直径18cm,内直径7cm,这块玉璧的面积是多少?
3.14×[(18÷2)2-(7÷2)2]
=3.14×(81-12.25)
=3.14×68.75
=215.875(cm2)
答:这块玉璧的面积是215.875平方厘米。
4
基础考题
3.下图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。
答:阴影部分面积为84.78平方厘米。
4
基础考题
S环=π×(R大2-r小2)
5.一个运动场如右图,两端是半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米?
周长:
3.14×32×2+100×2
= 400.96(米)
面积:
3.14×32 + 32×2×100
= 9615.36(平方米)
答:这个运动场的周长是400.96米;面积是 9615.36平方米。
4
基础考题
6.一个圆的周长是62.8m,半径增加了2m后,面积增加了多少?
62.8÷3.14÷2=10(m)
10+2=12(m)
3.14x12 -3.14×10 =138.16(m )
答:面积增加了138.16平方米。
考点1
7.有一根绳子长是31.4m,小红、小东和小林分别想用这根绳子在操场上围出一块地。怎样围面积最大?
在周长相等时,围成圆的面积最大。
我想
我想围成正方形。
我想
我想围成圆形。
考点2
5.下图是一块玉璧,外直径18cm,内直径
7cm,这块玉璧的面积是多少?
3.14×[(18÷2)2-(7÷2)2]
=3.14×(81-12.25)
=3.14×68.75
=215.875(cm2)
答:这块玉璧的面积是215.875平方厘米。
考点3
7.计算下面左边图形的周长和右边圆环的面积
考点5
考点6
考点8
12.土楼是福建、广东等地区的一种建筑形式,被列入“世界物质文化名录”,土楼的外围形状有圆形、方形、椭圆等。有两座地面是圆环形的土楼,其中一座外直径34m,内直径14m;另一座外直径26m,内直径也是4m。两座土楼的房屋占地面积相差多少?
3.14×[(34÷2) -(14÷2) ]=753.6(m )
3.14×[(26÷2) -(14÷2) ]=376.8(m )
相差面积:753.6-376.8=376.8(m2)
答:两座土楼的房屋占地面积相差376.8m 。
4
基础考题
3分线
6.75m
1.575m
3分线
6.75m
1.575m
考点10
你发现了什么?请你自己再任意设定一个正方形的边长,在正方形中画一个最大的国,看看是否也能得出相同的结论。
考点11
答:当周长一定时,所有图形中圆的面积最大。
蒙古包的底面做成圆形的,可以使居住的面积最大,
绝大多数的根和茎的横截面是圆形的,可以最大面积
地吸收水分。(合理即可)
17.为什么草原上蒙古包的底面是圆形的?为什么绝大多数的根和茎的横截面是圆形的?请你试着从数学的角度解释一下。
考点13
(1)在圆内剪去一个小圆就成为一个圆环。
( )
×
判断
必须是同心圆
(2)一个环形,外圆半径是4厘米,内圆直径是2厘米,计算这个环形的面积列式为:
3.14×42-3.14×22
( )
×
考点14
某公园内有一座圆形喷水池,它的半径是3米。现在要在喷水池周围铺上1米宽的甬路。甬路的占地面积是多少平方米?
3米
1米
3.14×4 -3.14×3
3+1=4(米)
=50.24-28.26
=21.98(平方米)
答:甬路的占地面积是21.98平方米。
方法一:
考点15
3.14×(4 -3 )
3+1=4(米)
=3.14×7
=21.98(平方米)
答:甬路的占地面积是21.98平方米。
方法二:
某公园内有一座圆形喷水池,它的半径是3米。现在要在喷水池周围铺上1米宽的甬路。甬路的占地面积是多少平方米?
3米
1米
考点15
一个圆环,外圆半径是6厘米,环宽1厘米。这个圆环的面积是多少?
r=6cm
3.14×(6 -5 )
6-1=5(米)
=3.14×11
=34.54(平方米)
答:这个圆环的面积是34.54平方米。
考点16
校园圆形花池的半径是6米,在花池的周围修一条1米宽的水泥路,求水泥路的面积是多少平方米?
3.14×(7 -6 )
6+1=7(米)
=3.14×13
=40.82(平方米)
答:水泥路的面积是40.82平方米。
考点17
7.“半径2厘米的圆,它的周长和面积相等”这句话对吗?为什么?
不对,周长和面积不能比。
辨析:没有真正理解圆的周长与面积的意义,一个是长度单位,一个是面积单位,没有相同不相同的说法,但是可以说数值相同。
考点19
5.5 圆的面积(2)
人教版六年级上册
易懂通课堂(用最简洁的方法让学生听懂重难点)
讲解设计:立足课本
1.基础部分
2.核心讲解
3.基础考点
4.核心考点
5.后面大量练习,先暂停页面,做完后听讲解核对。
圆
5
后面精彩片段截屏
什么叫圆环?
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
知识点1:求圆环的面积
一
基础部分
一个环形具有哪些特点?
(1)它们的圆心都在同一个点上(同心圆)。
(2)两个圆间的距离处处相等。
一
基础部分
·
r
R
r表示小圆半径
R表示大圆半径
环宽
说一说:
三个量之间的关系。
R=r+环宽
环宽=R-r
一
基础部分
请找出下面圆环的内圆半径(r)或外圆半径(R):
8厘米
R=( )厘米
8厘米
2厘米
r=( )厘米
6厘米
4厘米
r=( )厘米
3厘米
1厘米
R=( )厘米
4
2
2
4
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。圆环的面积是多少?
2
怎样利用内圆和外圆的面积求出圆环的面积?
一
核心讲解
2cm
6cm
3.14×6 -3.14×2
=3.14×36-3.14×4
=113.04-12.56
=100.48(平方厘米)
方法一:
答:它的面积是100.48平方厘米。
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。它的面积是多少?
(1)S环=πR2-πr2
2cm
6cm
=3.14×(36-4)
=3.14×32
3.14×(6 -2 )
方法二:
答:它的面积是100.48平方厘米。
=100.48(平方厘米)
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。它的面积是多少?
(2)S环=π×(R大2-r小2)
(1)S环=πR2-πr2
(2)S环=π×(R大2-r小2)
圆环的面积
2cm
6cm
3.14×6 -3.14×2
方法一:
3.14×(6 -2 )
方法二:
三
核心总结
圆环面积=外圆面积-内圆面积
50÷2=25(m) 10÷2=5(m)
答:草坪的占地面积是1884m 。
一个圆形环岛的直径是50m,中间是一个直径为10m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
3.14×(25 -5 )
=3.14×600
=1884(m )
4
基础考题
2.下图是一块玉璧,外直径18cm,内直径7cm,这块玉璧的面积是多少?
3.14×[(18÷2)2-(7÷2)2]
=3.14×(81-12.25)
=3.14×68.75
=215.875(cm2)
答:这块玉璧的面积是215.875平方厘米。
4
基础考题
3.下图中的大圆半径等于小圆的直径,请你求出阴影部分的面积。
答:阴影部分面积为84.78平方厘米。
4
基础考题
S环=π×(R大2-r小2)
5.一个运动场如右图,两端是半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米?
周长:
3.14×32×2+100×2
= 400.96(米)
面积:
3.14×32 + 32×2×100
= 9615.36(平方米)
答:这个运动场的周长是400.96米;面积是 9615.36平方米。
4
基础考题
6.一个圆的周长是62.8m,半径增加了2m后,面积增加了多少?
62.8÷3.14÷2=10(m)
10+2=12(m)
3.14x12 -3.14×10 =138.16(m )
答:面积增加了138.16平方米。
考点1
7.有一根绳子长是31.4m,小红、小东和小林分别想用这根绳子在操场上围出一块地。怎样围面积最大?
在周长相等时,围成圆的面积最大。
我想
我想围成正方形。
我想
我想围成圆形。
考点2
5.下图是一块玉璧,外直径18cm,内直径
7cm,这块玉璧的面积是多少?
3.14×[(18÷2)2-(7÷2)2]
=3.14×(81-12.25)
=3.14×68.75
=215.875(cm2)
答:这块玉璧的面积是215.875平方厘米。
考点3
7.计算下面左边图形的周长和右边圆环的面积
考点5
考点6
考点8
12.土楼是福建、广东等地区的一种建筑形式,被列入“世界物质文化名录”,土楼的外围形状有圆形、方形、椭圆等。有两座地面是圆环形的土楼,其中一座外直径34m,内直径14m;另一座外直径26m,内直径也是4m。两座土楼的房屋占地面积相差多少?
3.14×[(34÷2) -(14÷2) ]=753.6(m )
3.14×[(26÷2) -(14÷2) ]=376.8(m )
相差面积:753.6-376.8=376.8(m2)
答:两座土楼的房屋占地面积相差376.8m 。
4
基础考题
3分线
6.75m
1.575m
3分线
6.75m
1.575m
考点10
你发现了什么?请你自己再任意设定一个正方形的边长,在正方形中画一个最大的国,看看是否也能得出相同的结论。
考点11
答:当周长一定时,所有图形中圆的面积最大。
蒙古包的底面做成圆形的,可以使居住的面积最大,
绝大多数的根和茎的横截面是圆形的,可以最大面积
地吸收水分。(合理即可)
17.为什么草原上蒙古包的底面是圆形的?为什么绝大多数的根和茎的横截面是圆形的?请你试着从数学的角度解释一下。
考点13
(1)在圆内剪去一个小圆就成为一个圆环。
( )
×
判断
必须是同心圆
(2)一个环形,外圆半径是4厘米,内圆直径是2厘米,计算这个环形的面积列式为:
3.14×42-3.14×22
( )
×
考点14
某公园内有一座圆形喷水池,它的半径是3米。现在要在喷水池周围铺上1米宽的甬路。甬路的占地面积是多少平方米?
3米
1米
3.14×4 -3.14×3
3+1=4(米)
=50.24-28.26
=21.98(平方米)
答:甬路的占地面积是21.98平方米。
方法一:
考点15
3.14×(4 -3 )
3+1=4(米)
=3.14×7
=21.98(平方米)
答:甬路的占地面积是21.98平方米。
方法二:
某公园内有一座圆形喷水池,它的半径是3米。现在要在喷水池周围铺上1米宽的甬路。甬路的占地面积是多少平方米?
3米
1米
考点15
一个圆环,外圆半径是6厘米,环宽1厘米。这个圆环的面积是多少?
r=6cm
3.14×(6 -5 )
6-1=5(米)
=3.14×11
=34.54(平方米)
答:这个圆环的面积是34.54平方米。
考点16
校园圆形花池的半径是6米,在花池的周围修一条1米宽的水泥路,求水泥路的面积是多少平方米?
3.14×(7 -6 )
6+1=7(米)
=3.14×13
=40.82(平方米)
答:水泥路的面积是40.82平方米。
考点17
7.“半径2厘米的圆,它的周长和面积相等”这句话对吗?为什么?
不对,周长和面积不能比。
辨析:没有真正理解圆的周长与面积的意义,一个是长度单位,一个是面积单位,没有相同不相同的说法,但是可以说数值相同。
考点19
