第五章·统计与概率章节检测 -2021-2022学年高一上学期数学人教B版(2019)必修第二册(Word含答案解析)
文档属性
| 名称 | 第五章·统计与概率章节检测 -2021-2022学年高一上学期数学人教B版(2019)必修第二册(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 397.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-24 21:42:29 | ||
图片预览



文档简介
北京·高一·同步练习
统计与概率·章节检测
一、选择题(共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项)
1.若经检验,某厂的产品合格率为98%,估算该厂8000件产品中的次品件数为( )
A.7840 B.160 C.16 D.784
2.从10个事件中任取一个事件,若这个事件是必然事件的概率为0.2,是不可能事件的概率为0.3,则这10个事件中随机事件的个数是( )
A.3 B.4 C.5 D.6
3.有一笔统计资料,共有11个如下数据(不完全以大小排列):2,4,4,5,5,6,7,8,9,11,x,已知这组数据的平均数为6,则这组数据的方差为( )
A.6 B. C.66 D.6.5
4.给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件;②“当x为某一实数时,可使x2≤0”是不可能事件;③“明天天津市要下雨”是必然事件;④“从100个灯泡(含有10个次品)中取出5个,5个全是次品”是随机事件.
其中正确命题的个数是( )
A.0 B.1
C.2 D.3
5.下列说法中,正确的是 ( )
A.数据5,4,4,3,5,2的众数是4
B.一组数据的标准差的平方是这组数据的方差
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.频率分布直方图中各小矩形的面积等于相应各组的频数
6.若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( )
A.91.5和91.5 B.91.5和92 C.91和91.5 D.92和92
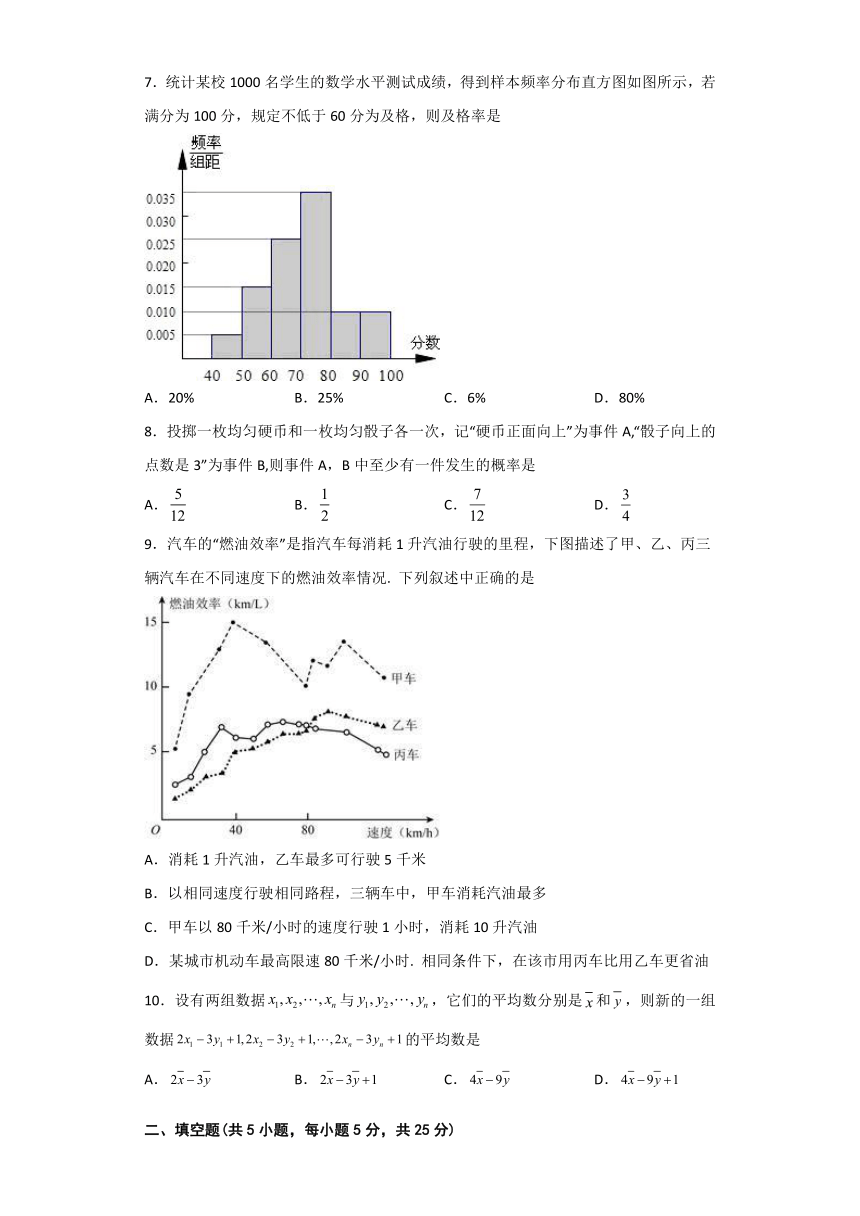
7.统计某校1000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是
A.20% B.25% C.6% D.80%
8.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A,B中至少有一件发生的概率是
A. B. C. D.
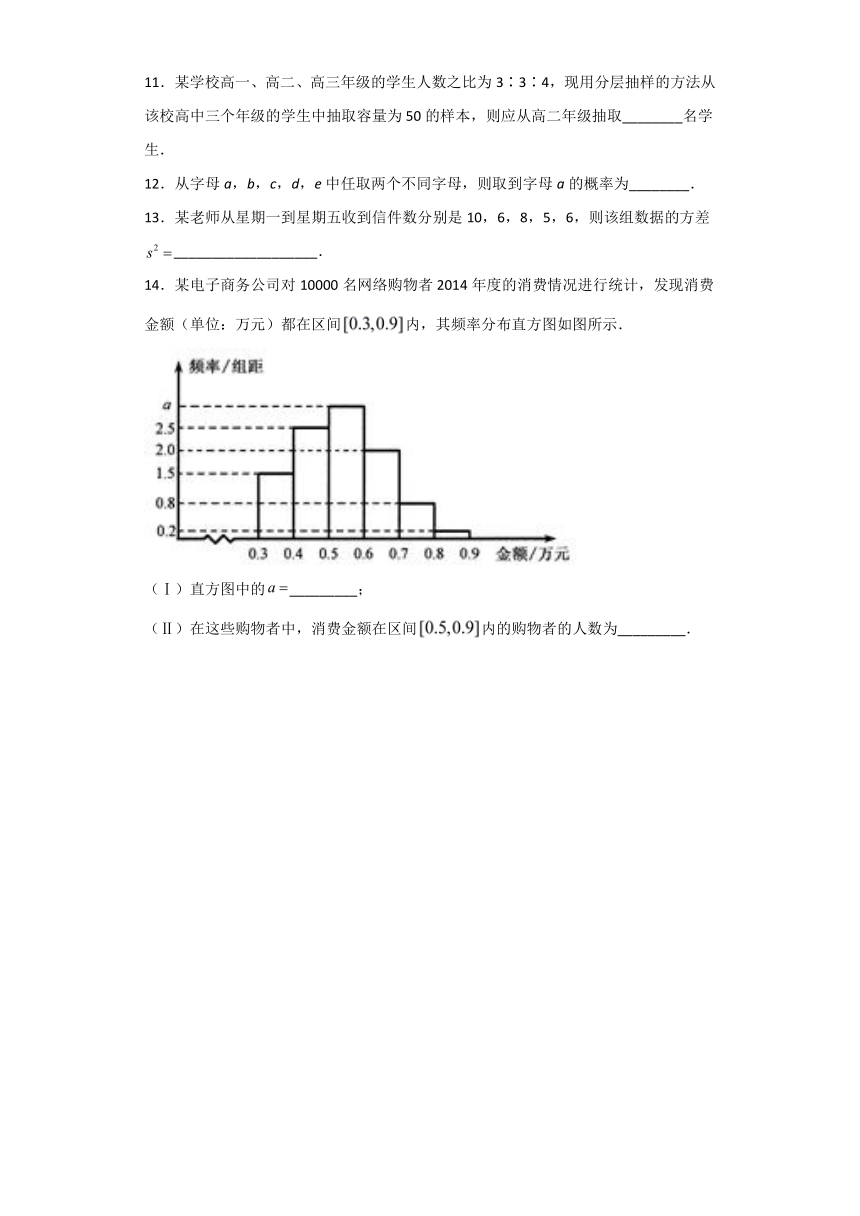
9.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
10.设有两组数据与,它们的平均数分别是和,则新的一组数据的平均数是
A. B. C. D.
二、填空题(共5小题,每小题5分,共25分)
11.某学校高一、高二、高三年级的学生人数之比为3∶3∶4,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取________名学生.
12.从字母a,b,c,d,e中任取两个不同字母,则取到字母a的概率为________.
13.某老师从星期一到星期五收到信件数分别是10,6,8,5,6,则该组数据的方差___________________.
14.某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间内,其频率分布直方图如图所示.
(Ⅰ)直方图中的_________;
(Ⅱ)在这些购物者中,消费金额在区间内的购物者的人数为_________.
15.辛普森悖论(Simpson’sParadox)有人译为辛普森诡论,在统计学中亦有人称为“逆论”,甚至有人视之为“魔术”.辛普森悖论为英国统计学家E.H.辛普森(E.H.Simpson)于1951年提出的,辛普森悖论的内容大意是“在某个条件下的两组数据,分别讨论时都会满足某种性质,可是一旦合并考虑,却可能导致相反的结论.”下面这个案例可以让我们感受到这个悖论:关于某高校法学院和商学院新学期已完成的招生情况,现有如下数据:
某高校 申请人数 性别 录取率
法学院 200人 男 50%
女 70%
商学院 300人 男 60%
女 90%
对于此次招生,给出下列四个结论:
①法学院的录取率小于商学院的录取率;
②这两个学院所有男生的录取率小于这两个学院所有女生的录取率;
③这两个学院所有男生的录取率不一定小于这两个学院所有女生的录取率;
④法学院的录取率不一定小于这两个学院所有学生的录取率.
其中,所有正确结论的序号是___________.
三、解答题(共6小题,共85分。解答应写出文字说明、演算步骤或证明过程)
16.为缓解交通运行压力,某市公交系统实施疏堵工程.现调取某路公交车早高峰时段全程运输时间(单位:分钟)的数据,从疏堵工程完成前的数据中随机抽取5个数据,记为组;从疏堵工程完成后的数据中随机抽取5个数据,记为组.
组:
组:
(Ⅰ)该路公交车全程运输时间不超过分钟,称为“正点运行”.从,两组数据中各随机抽取一个数据,求这两个数据对应的两次运行中至少有一次“正点运行”的概率;
(Ⅱ)试比较,两组数据方差的大小(不要求计算),并说明其实际意义.
17.某中学有学生500人,学校为了解学生课外阅读时间,从中随机抽取了50名学生,收集了他们2018年10月课外阅读时间(单位:小时)的数据,并将数据进行整理,分为5组:[10,12),[12,14),[14,16),[16,18),[18,20],得到如图所示的频率分布直方图.
(Ⅰ)试估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数;
(Ⅱ)已知这50名学生中恰有2名女生的课外阅读时间在[18,20],现从课外阅读时间在[18,20]的样本对应的学生中随机抽取2人,求至少抽到1名女生的概率;
(Ⅲ)假设同组中的每个数据用该组区间的中点值代替,试估计该校学生2018年10月课外阅读时间的平均数.
18.我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨)、一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照,分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使的居民每月的用水量不超过标准(吨),估计的值,并说明理由.
19.某市对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高),现从参赛者中抽取了x人,按年龄分成5组(第一组:[20,25),第二组:[25,30),第三组:[30,35),第四组:[35,40),第五组:[40,45]),得到如图所示的频率分布直方图,已知第一组有5人.
(1)求x;
(2)求抽取的x人的年龄的50%分位数(结果保留整数);
(3)以下是参赛的10人的成绩:90,96,97,95,92,92,98,88,96,99,求这10人成绩的20%分位数和平均数,以这两个数据为依据,评价参赛人员对一带一路的认知程度,并谈谈你的感想.
20.某市高中全体学生参加某项测评,按得分评为两类(评定标准见表1).根据男女学生比例,使用分层抽样的方法随机抽取了10000名学生的得分数据,其中等级为的学生中有40%是男生,等级为的学生中有一半是女生.等级为和的学生统称为类学生,等级为和的学生统称为类学生.整理这10000名学生的得分数据,得到如图2所示的频率分布直方图,
类别 得分()
表1
(I)已知该市高中学生共20万人,试估计在该项测评中被评为类学生的人数;
(Ⅱ)某5人得分分别为45,50,55,75,85.从这5人中随机选取2人组成甲组,另外3人组成乙组,求“甲、乙两组各有1名类学生”的概率;
(Ⅲ)在这10000名学生中,男生占总数的比例为51%,类女生占女生总数的比例为,类男生占男生总数的比例为,判断与的大小.(只需写出结论)
21.为迎接2022年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记表示学生的考核成绩,并规定为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图:
(1)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核优秀的概率;
(2)从图中考核成绩满足的学生中任取2人,求至少有一人考核优秀的概率;
(3)记表示学生的考核成绩在区间的概率,根据以往培训数据,规定当时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
试卷第4页,共7页
参考答案
1.B
【分析】
根据合格率可得次品率,再用产品总数乘以次品率即可得到次品的数量.
【详解】
解:由题意合格率为98%,则次品率为
故8000件产品中的次品件数为
故选:B
【点睛】
本题考查概率的应用,属于基础题.
2.C
【分析】
分别求出必然事件、不可能事件的个数,总数减去这两种事件的个数即可求得随机事件的个数.
【详解】
这10个事件中,必然事件的个数为,不可能事件的个数为.而必然事件、不可能事件、随机事件是彼此互斥的事件,且它们的个数和为10,故随机事件的个数为.
故选C.
【点睛】
本题考查必然事件、不可能事件、随机事件的定义,互斥事件,属于基础题.
3.A
【详解】
分析:根据方差的计算公式计算即可,先必须求这组数据2,4,4,…的平均数后求方差.
解:由=(2+4+4+…+11+x)=6
得x=5.
∴s2=[(6-2)2+(6-4)2+…+(6-11)2+(6-5)2]=6.
故选A.
点评:本题考查平均数与方差的定义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1-)2+(x2-)2+…+(xn-)2].
4.C
【分析】
利用必然事件的概念可以判断①是正确的命题,③是偶然事件,利用不可能事件的概念判断②正确,利用随机事件的概念判断④正确.
【详解】
对于①,三个球全部放入两个盒子,有两种情况:1+2和3+0,故必有一个盒子有一个以上的球,所以该事件是必然事件,①正确;
对于②,x=0时x2=0,所以该事件不是不可能事件,②错误;
对于③,“明天天津市要下雨”是偶然事件,所以该事件是随机事件,③错误;
对于④,“从100个灯泡(含有10个次品)中取出5个,5个全是次品”,发生与否是随机的,所以该事件是随机事件,④正确.故正确命题有2个.
故选:C.
5.C
【详解】
数据5,4,4,3,5,2的众数是4和5,A错;
一组数据的标准差是这组数据的方差的算术平方根,B错;
由标准差公式知C正确;
频率分布直方图中各小长方形的面积等于相应各组的频率,D错.
故选:C.
6.A
【详解】
8个班参加合唱比赛的得分从小到大排列分别是87,89,90,91,92,93,94,96,中位数是91,92,的平均数91.5,平均数是=91.5
7.D
【详解】
解:及格的频率为(0.025+0.035+0.01+0.01)×10=0.8=80%故选D:
8.C
【详解】
试题分析:由题意可知,事件A与事件B是相互独立的,而事件A、B中至少有一件发生的事件包含、、,又,,所以所事件的概率为,故选C.
考点:相互独立事件概率的计算.
9.D
【详解】
解:对于A,由图象可知当速度大于40km/h时,乙车的燃油效率大于5km/L,
∴当速度大于40km/h时,消耗1升汽油,乙车的行驶距离大于5km,故A错误;
对于B,由图象可知当速度相同时,甲车的燃油效率最高,即当速度相同时,消耗1升汽油,甲车的行驶路程最远,
∴以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少,故B错误;
对于C,由图象可知当速度为80km/h时,甲车的燃油效率为10km/L,
即甲车行驶10km时,耗油1升,故行驶1小时,路程为80km,燃油为8升,故C错误;
对于D,由图象可知当速度小于80km/h时,丙车的燃油效率大于乙车的燃油效率,
∴用丙车比用乙车更省油,故D正确
故选D.
考点:1、数学建模能力;2、阅读能力及化归思想.
10.B
【分析】
由题意结合平均数的性质即可求得结果.
【详解】
由题意结合平均数的性质可知:
的平均数为,
的平均数为,
则的平均数为:.
故选:B.
11.15
【详解】
试题分析:应从高二年级学生中抽取名学生,故应填.
考点:分层抽样及运用.
12.
【解析】
试题分析:从字母,,,,中任取两个不同字母,有(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e)共10种,其中包含a的有4种,所以所求的概率为.
考点:考查了古典概型.
点评:解本题的关键把字母不同的取法一一列出来,再找出包含字母a的,利用概率公式求出概率.
13.
【详解】
试题分析:由平均数及方差的定义可得;
.
考点:样本数据的数字特征:平均值与方差.
14.(Ⅰ)3;(Ⅱ)6000.
【详解】
由频率分布直方图及频率和等于1可得,
解之得.于是消费金额在区间内频率为,所以消费金额在区间内的购物者的人数为:,故应填3;6000.
考点:本题考查频率分布直方图,属基础题.
15.②④
【分析】
根据题意,结合古典概型的概率计算公式,逐项进行判定,即可求解.
【详解】
设申请法学院的男生人数为,女生人数为,则,
法学院的录取率为,
设申请商学院的男生人数为,女生人数为,则,
商学院的录取率为,
由,
该值的正负不确定,所以①错误,④正确;
这两个学院所有男生的录取率为,
这两个学院所有女生的录取率为,
因为,
所以②正确;③错误.
故答案为:②④.
【点睛】
本题主要考查了古典概型的概率公式的应用,其中解答中正确理解题意,结合古典概型的概率计算公式求得相应的概率是解答的关键,着重考查数学阅读能力,属于基础题.
16.(Ⅰ);(Ⅱ)组数据的方差小于组数据的方差.说明疏堵工程完成后,该路公交车全程运输时间更加稳定,而且“正点运行”率高,运行更加有保障..
【分析】
(Ⅰ)先求出从,两组数据中各随机抽取一个数据,不同的取法的种数,在求出两个数据对应的两次运行中至少有一次“正点运行”的种数,最后利用古典概型计算公式,求出概率;
(Ⅱ)可以通过数据的波动情况判断出方差的大小,最后得出结论.
【详解】
(Ⅰ)解:从,两组数据中各随机抽取一个数据,所有不同的取法共有种.
从组中取到时,组中符合题意的取法为,
共种;
从组中取到时,组中符合题意的取法为,
共种;
因此符合题意的取法共有种,
所以该路公交车至少有一次“正点运行”的概率.
(Ⅱ)解:组数据的方差小于组数据的方差.说明疏堵工程完成后,该路公交车全程运输时间更加稳定,而且“正点运行”率高,运行更加有保障.
【点睛】
本题考查了古典概型概率的计算方法,考查了用方差解决实际问题的能力.
17.(Ⅰ)150(Ⅱ)(Ⅲ)14.68
【分析】
(Ⅰ)由频率分布直方图求出课外阅读时间不小于16小时的样本的频率为0.30,由此能估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数;(Ⅱ)阅读时间在[18,20]的样本的频率为0.10.从而课外阅读时间在[18,20]的样本对应的学生人数为5.这5名学生中有2名女生,3名男生,设女生为A,B,男生为C,D,E,从中抽取2人,利用列举法能求出至少抽到1名女生的概率;(Ⅲ)由频率分布直方图能估计该校学生2018年10月课外阅读时间的平均数.
【详解】
(Ⅰ)0.10×2+0.05×2=0.30,
即课外阅读时间不小于16小时的样本的频率为0.30.
因为500×0.30=150,
所以估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数为150.
(Ⅱ)阅读时间在[18,20]的样本的频率为0.05×2=0.10.
因为50×0.10=5,即课外阅读时间在[18,20]的样本对应的学生人数为5.
这5名学生中有2名女生,3名男生,设女生为A,B,男生为C,D,E,
从中抽取2人的所有可能结果是:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E).
其中至少抽到1名女生的结果有7个,
所以从课外阅读时间在[18,20]的样本对应的学生中随机抽取2人,至少抽到1名女生的概率为p=
(Ⅲ)根据题意,0.08×2×11+0.12×2×13+0.15×2×15+0.10×2×17+0.05×2×19=14.68(小时).
由此估计该校学生2018年10月课外阅读时间的平均数为14.68小时.
【点睛】
本题考查频数、概率、平均数的求法,考查频率分布直方图、列举法等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.
18.(1);(2)万;(3).
【详解】
试题分析:本题主要考查频率分布直方图、频率、频数的计算等基础知识,考查学生的分析问题、解决问题的能力. 第(1)问,由高×组距=频率,计算每组的频率,根据所有频率之和为1,计算出a的值;第(2)问,利用高×组距=频率,先计算出每人月均用水量不低于3吨的频率,再利用频率×样本容量=频数,计算所求人数;第(3)问,将前6组的频率之和与前5组的频率之和进行比较,得出2.5≤x<3,再估计x的值.
试题解析:(1)由频率分布直方图知,月均用水量在[0,0.5)中的频率为0.08×0.5=0.04,
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5)中的频率分别为0.08,0.20,0.26,0.06,0.04,0.02.
由0.04+0.08+0.5×a+0.20+0.26+0.5×a+0.06+0.04+0.02=1,
解得a=0.30.
(2)由(1),100位居民每人月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计全市30万居民中月均用水量不低于3吨的人数为
300 000×0.12="36" 000.
(3)因为前6组的频率之和为0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85,
而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85,
所以2.5≤x<3.
由0.3×(x–2.5)=0.85–0.73,
解得x=2.9.
所以,估计月用水量标准为2.9吨时,85%的居民每月的用水量不超过标准.
【考点】
频率分布直方图
【名师点睛】
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,考查学生的分析问题、解决问题的能力.在频率分布直方图中,第n个小矩形的面积就是相应组的频率,所有小矩形的面积之和为1,这是解题的关键,也是识图的基础.
19.(1)100;(2)32;(3)20%分位数为91;平均数为94.3;答案见解析.
【分析】
(1)求出频率,利用频率即可得解;
(2)利用百分位数的定义即可求解;
(3)利用百分位数的定义及平均数的定义计算可得解,再作出评价和感想.
【详解】
(1)第一组频率为0.01×5=0.05,所以.
(2)由题图可知年龄低于30岁的所占比例为,年龄低于35岁的所占比例为,
所以抽取的x人的年龄的分位数在内,
由,所以抽取的x人的年龄的分位数为32.
(3)把参赛的10人的成绩按从小到大的顺序排列:88,90,92,92,95,96,96,97,98,99,
计算,所以这10人成绩的分位数为,
这10人成绩的平均数为
评价:从百分位数和平均数来看,参赛人员的认知程度很高.
感想:结合本题和实际,符合社会主义核心价值观即可.
【点睛】
关键点点睛:本题考查频率,频数,总数的关系及第百分位数的计算,理解第百分位数的定义及应用是解题的关键,考查学生的计算能力,属于一般题.
20.(Ⅰ)8万人;(Ⅱ);(Ⅲ).
【详解】
试题分析:(I)根据直方图可得样本中类学生所占比例为,所以类学生所占比例为,再根据总人数可估计在该项测评中被评为类学生的人数;(Ⅱ)利用列举法列举出按要求分成两组,分组的方法数为种,其中“甲、乙两组各有名类学生”的方法共有种,由古典概型概率公式可得结果;(Ⅲ)根据直方图,结合表格数据可得结论.
试题解析:(1)依题意得,样本中类学生所占比例为,
所以类学生所占比例为. 因为全市高中学生共万人,
所以在该项测评中被评为类学生的人数约为8万人.
(2)由表1得,在5人(记为)中,类学生有2人(不妨设为).
将他们按要求分成两组,分组的方法数为种.
依次为: .
所以“甲、乙两组各有一名类学生”的概率为.
(3).
21.(1);(2);(3)有效,理由见解析.
【分析】
(1)设这名学生考核优秀为事件,利用古典概型的概率公式求解;
(2)设至少有一人考核成绩优秀为事件,再利用古典概型的概率公式求解;
(3)根据表格中的数据,满足的成绩有16个,即得解.
【详解】
(1)设这名学生考核优秀为事件,
由茎叶图中的数据可以知道,30名同学中,有7名同学考核优秀,
所以所求概率约为.
(2)设从图中考核成绩满足的学生中任取2人,
至少有一人考核成绩优秀为事件,因为表中成绩在的6人中有2个人考核为优,
所以基本事件空间包含15个基本事件,它们是
事件包含9个基本事件,它们是
所以.
(3)根据表格中的数据,满足的成绩有16个,
所以
所以可以认为此次冰雪培训活动有效.
【点睛】
本题主要考查茎叶图,考查古典概型的概率的计算,意在考查学生对这些知识的理解掌握水平.
北京·高一·
统计与概率·章节检测
一、选择题(共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项)
1.若经检验,某厂的产品合格率为98%,估算该厂8000件产品中的次品件数为( )
A.7840 B.160 C.16 D.784
2.从10个事件中任取一个事件,若这个事件是必然事件的概率为0.2,是不可能事件的概率为0.3,则这10个事件中随机事件的个数是( )
A.3 B.4 C.5 D.6
3.有一笔统计资料,共有11个如下数据(不完全以大小排列):2,4,4,5,5,6,7,8,9,11,x,已知这组数据的平均数为6,则这组数据的方差为( )
A.6 B. C.66 D.6.5
4.给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件;②“当x为某一实数时,可使x2≤0”是不可能事件;③“明天天津市要下雨”是必然事件;④“从100个灯泡(含有10个次品)中取出5个,5个全是次品”是随机事件.
其中正确命题的个数是( )
A.0 B.1
C.2 D.3
5.下列说法中,正确的是 ( )
A.数据5,4,4,3,5,2的众数是4
B.一组数据的标准差的平方是这组数据的方差
C.数据2,3,4,5的方差是数据4,6,8,10的方差的一半
D.频率分布直方图中各小矩形的面积等于相应各组的频数
6.若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数和平均数分别是( )
A.91.5和91.5 B.91.5和92 C.91和91.5 D.92和92
7.统计某校1000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是
A.20% B.25% C.6% D.80%
8.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A,B中至少有一件发生的概率是
A. B. C. D.
9.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
10.设有两组数据与,它们的平均数分别是和,则新的一组数据的平均数是
A. B. C. D.
二、填空题(共5小题,每小题5分,共25分)
11.某学校高一、高二、高三年级的学生人数之比为3∶3∶4,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取________名学生.
12.从字母a,b,c,d,e中任取两个不同字母,则取到字母a的概率为________.
13.某老师从星期一到星期五收到信件数分别是10,6,8,5,6,则该组数据的方差___________________.
14.某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间内,其频率分布直方图如图所示.
(Ⅰ)直方图中的_________;
(Ⅱ)在这些购物者中,消费金额在区间内的购物者的人数为_________.
15.辛普森悖论(Simpson’sParadox)有人译为辛普森诡论,在统计学中亦有人称为“逆论”,甚至有人视之为“魔术”.辛普森悖论为英国统计学家E.H.辛普森(E.H.Simpson)于1951年提出的,辛普森悖论的内容大意是“在某个条件下的两组数据,分别讨论时都会满足某种性质,可是一旦合并考虑,却可能导致相反的结论.”下面这个案例可以让我们感受到这个悖论:关于某高校法学院和商学院新学期已完成的招生情况,现有如下数据:
某高校 申请人数 性别 录取率
法学院 200人 男 50%
女 70%
商学院 300人 男 60%
女 90%
对于此次招生,给出下列四个结论:
①法学院的录取率小于商学院的录取率;
②这两个学院所有男生的录取率小于这两个学院所有女生的录取率;
③这两个学院所有男生的录取率不一定小于这两个学院所有女生的录取率;
④法学院的录取率不一定小于这两个学院所有学生的录取率.
其中,所有正确结论的序号是___________.
三、解答题(共6小题,共85分。解答应写出文字说明、演算步骤或证明过程)
16.为缓解交通运行压力,某市公交系统实施疏堵工程.现调取某路公交车早高峰时段全程运输时间(单位:分钟)的数据,从疏堵工程完成前的数据中随机抽取5个数据,记为组;从疏堵工程完成后的数据中随机抽取5个数据,记为组.
组:
组:
(Ⅰ)该路公交车全程运输时间不超过分钟,称为“正点运行”.从,两组数据中各随机抽取一个数据,求这两个数据对应的两次运行中至少有一次“正点运行”的概率;
(Ⅱ)试比较,两组数据方差的大小(不要求计算),并说明其实际意义.
17.某中学有学生500人,学校为了解学生课外阅读时间,从中随机抽取了50名学生,收集了他们2018年10月课外阅读时间(单位:小时)的数据,并将数据进行整理,分为5组:[10,12),[12,14),[14,16),[16,18),[18,20],得到如图所示的频率分布直方图.
(Ⅰ)试估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数;
(Ⅱ)已知这50名学生中恰有2名女生的课外阅读时间在[18,20],现从课外阅读时间在[18,20]的样本对应的学生中随机抽取2人,求至少抽到1名女生的概率;
(Ⅲ)假设同组中的每个数据用该组区间的中点值代替,试估计该校学生2018年10月课外阅读时间的平均数.
18.我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨)、一位居民的月用水量不超过的部分按平价收费,超出的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照,分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使的居民每月的用水量不超过标准(吨),估计的值,并说明理由.
19.某市对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高),现从参赛者中抽取了x人,按年龄分成5组(第一组:[20,25),第二组:[25,30),第三组:[30,35),第四组:[35,40),第五组:[40,45]),得到如图所示的频率分布直方图,已知第一组有5人.
(1)求x;
(2)求抽取的x人的年龄的50%分位数(结果保留整数);
(3)以下是参赛的10人的成绩:90,96,97,95,92,92,98,88,96,99,求这10人成绩的20%分位数和平均数,以这两个数据为依据,评价参赛人员对一带一路的认知程度,并谈谈你的感想.
20.某市高中全体学生参加某项测评,按得分评为两类(评定标准见表1).根据男女学生比例,使用分层抽样的方法随机抽取了10000名学生的得分数据,其中等级为的学生中有40%是男生,等级为的学生中有一半是女生.等级为和的学生统称为类学生,等级为和的学生统称为类学生.整理这10000名学生的得分数据,得到如图2所示的频率分布直方图,
类别 得分()
表1
(I)已知该市高中学生共20万人,试估计在该项测评中被评为类学生的人数;
(Ⅱ)某5人得分分别为45,50,55,75,85.从这5人中随机选取2人组成甲组,另外3人组成乙组,求“甲、乙两组各有1名类学生”的概率;
(Ⅲ)在这10000名学生中,男生占总数的比例为51%,类女生占女生总数的比例为,类男生占男生总数的比例为,判断与的大小.(只需写出结论)
21.为迎接2022年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记表示学生的考核成绩,并规定为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图:
(1)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核优秀的概率;
(2)从图中考核成绩满足的学生中任取2人,求至少有一人考核优秀的概率;
(3)记表示学生的考核成绩在区间的概率,根据以往培训数据,规定当时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
试卷第4页,共7页
参考答案
1.B
【分析】
根据合格率可得次品率,再用产品总数乘以次品率即可得到次品的数量.
【详解】
解:由题意合格率为98%,则次品率为
故8000件产品中的次品件数为
故选:B
【点睛】
本题考查概率的应用,属于基础题.
2.C
【分析】
分别求出必然事件、不可能事件的个数,总数减去这两种事件的个数即可求得随机事件的个数.
【详解】
这10个事件中,必然事件的个数为,不可能事件的个数为.而必然事件、不可能事件、随机事件是彼此互斥的事件,且它们的个数和为10,故随机事件的个数为.
故选C.
【点睛】
本题考查必然事件、不可能事件、随机事件的定义,互斥事件,属于基础题.
3.A
【详解】
分析:根据方差的计算公式计算即可,先必须求这组数据2,4,4,…的平均数后求方差.
解:由=(2+4+4+…+11+x)=6
得x=5.
∴s2=[(6-2)2+(6-4)2+…+(6-11)2+(6-5)2]=6.
故选A.
点评:本题考查平均数与方差的定义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1-)2+(x2-)2+…+(xn-)2].
4.C
【分析】
利用必然事件的概念可以判断①是正确的命题,③是偶然事件,利用不可能事件的概念判断②正确,利用随机事件的概念判断④正确.
【详解】
对于①,三个球全部放入两个盒子,有两种情况:1+2和3+0,故必有一个盒子有一个以上的球,所以该事件是必然事件,①正确;
对于②,x=0时x2=0,所以该事件不是不可能事件,②错误;
对于③,“明天天津市要下雨”是偶然事件,所以该事件是随机事件,③错误;
对于④,“从100个灯泡(含有10个次品)中取出5个,5个全是次品”,发生与否是随机的,所以该事件是随机事件,④正确.故正确命题有2个.
故选:C.
5.C
【详解】
数据5,4,4,3,5,2的众数是4和5,A错;
一组数据的标准差是这组数据的方差的算术平方根,B错;
由标准差公式知C正确;
频率分布直方图中各小长方形的面积等于相应各组的频率,D错.
故选:C.
6.A
【详解】
8个班参加合唱比赛的得分从小到大排列分别是87,89,90,91,92,93,94,96,中位数是91,92,的平均数91.5,平均数是=91.5
7.D
【详解】
解:及格的频率为(0.025+0.035+0.01+0.01)×10=0.8=80%故选D:
8.C
【详解】
试题分析:由题意可知,事件A与事件B是相互独立的,而事件A、B中至少有一件发生的事件包含、、,又,,所以所事件的概率为,故选C.
考点:相互独立事件概率的计算.
9.D
【详解】
解:对于A,由图象可知当速度大于40km/h时,乙车的燃油效率大于5km/L,
∴当速度大于40km/h时,消耗1升汽油,乙车的行驶距离大于5km,故A错误;
对于B,由图象可知当速度相同时,甲车的燃油效率最高,即当速度相同时,消耗1升汽油,甲车的行驶路程最远,
∴以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少,故B错误;
对于C,由图象可知当速度为80km/h时,甲车的燃油效率为10km/L,
即甲车行驶10km时,耗油1升,故行驶1小时,路程为80km,燃油为8升,故C错误;
对于D,由图象可知当速度小于80km/h时,丙车的燃油效率大于乙车的燃油效率,
∴用丙车比用乙车更省油,故D正确
故选D.
考点:1、数学建模能力;2、阅读能力及化归思想.
10.B
【分析】
由题意结合平均数的性质即可求得结果.
【详解】
由题意结合平均数的性质可知:
的平均数为,
的平均数为,
则的平均数为:.
故选:B.
11.15
【详解】
试题分析:应从高二年级学生中抽取名学生,故应填.
考点:分层抽样及运用.
12.
【解析】
试题分析:从字母,,,,中任取两个不同字母,有(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e)共10种,其中包含a的有4种,所以所求的概率为.
考点:考查了古典概型.
点评:解本题的关键把字母不同的取法一一列出来,再找出包含字母a的,利用概率公式求出概率.
13.
【详解】
试题分析:由平均数及方差的定义可得;
.
考点:样本数据的数字特征:平均值与方差.
14.(Ⅰ)3;(Ⅱ)6000.
【详解】
由频率分布直方图及频率和等于1可得,
解之得.于是消费金额在区间内频率为,所以消费金额在区间内的购物者的人数为:,故应填3;6000.
考点:本题考查频率分布直方图,属基础题.
15.②④
【分析】
根据题意,结合古典概型的概率计算公式,逐项进行判定,即可求解.
【详解】
设申请法学院的男生人数为,女生人数为,则,
法学院的录取率为,
设申请商学院的男生人数为,女生人数为,则,
商学院的录取率为,
由,
该值的正负不确定,所以①错误,④正确;
这两个学院所有男生的录取率为,
这两个学院所有女生的录取率为,
因为,
所以②正确;③错误.
故答案为:②④.
【点睛】
本题主要考查了古典概型的概率公式的应用,其中解答中正确理解题意,结合古典概型的概率计算公式求得相应的概率是解答的关键,着重考查数学阅读能力,属于基础题.
16.(Ⅰ);(Ⅱ)组数据的方差小于组数据的方差.说明疏堵工程完成后,该路公交车全程运输时间更加稳定,而且“正点运行”率高,运行更加有保障..
【分析】
(Ⅰ)先求出从,两组数据中各随机抽取一个数据,不同的取法的种数,在求出两个数据对应的两次运行中至少有一次“正点运行”的种数,最后利用古典概型计算公式,求出概率;
(Ⅱ)可以通过数据的波动情况判断出方差的大小,最后得出结论.
【详解】
(Ⅰ)解:从,两组数据中各随机抽取一个数据,所有不同的取法共有种.
从组中取到时,组中符合题意的取法为,
共种;
从组中取到时,组中符合题意的取法为,
共种;
因此符合题意的取法共有种,
所以该路公交车至少有一次“正点运行”的概率.
(Ⅱ)解:组数据的方差小于组数据的方差.说明疏堵工程完成后,该路公交车全程运输时间更加稳定,而且“正点运行”率高,运行更加有保障.
【点睛】
本题考查了古典概型概率的计算方法,考查了用方差解决实际问题的能力.
17.(Ⅰ)150(Ⅱ)(Ⅲ)14.68
【分析】
(Ⅰ)由频率分布直方图求出课外阅读时间不小于16小时的样本的频率为0.30,由此能估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数;(Ⅱ)阅读时间在[18,20]的样本的频率为0.10.从而课外阅读时间在[18,20]的样本对应的学生人数为5.这5名学生中有2名女生,3名男生,设女生为A,B,男生为C,D,E,从中抽取2人,利用列举法能求出至少抽到1名女生的概率;(Ⅲ)由频率分布直方图能估计该校学生2018年10月课外阅读时间的平均数.
【详解】
(Ⅰ)0.10×2+0.05×2=0.30,
即课外阅读时间不小于16小时的样本的频率为0.30.
因为500×0.30=150,
所以估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数为150.
(Ⅱ)阅读时间在[18,20]的样本的频率为0.05×2=0.10.
因为50×0.10=5,即课外阅读时间在[18,20]的样本对应的学生人数为5.
这5名学生中有2名女生,3名男生,设女生为A,B,男生为C,D,E,
从中抽取2人的所有可能结果是:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E).
其中至少抽到1名女生的结果有7个,
所以从课外阅读时间在[18,20]的样本对应的学生中随机抽取2人,至少抽到1名女生的概率为p=
(Ⅲ)根据题意,0.08×2×11+0.12×2×13+0.15×2×15+0.10×2×17+0.05×2×19=14.68(小时).
由此估计该校学生2018年10月课外阅读时间的平均数为14.68小时.
【点睛】
本题考查频数、概率、平均数的求法,考查频率分布直方图、列举法等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.
18.(1);(2)万;(3).
【详解】
试题分析:本题主要考查频率分布直方图、频率、频数的计算等基础知识,考查学生的分析问题、解决问题的能力. 第(1)问,由高×组距=频率,计算每组的频率,根据所有频率之和为1,计算出a的值;第(2)问,利用高×组距=频率,先计算出每人月均用水量不低于3吨的频率,再利用频率×样本容量=频数,计算所求人数;第(3)问,将前6组的频率之和与前5组的频率之和进行比较,得出2.5≤x<3,再估计x的值.
试题解析:(1)由频率分布直方图知,月均用水量在[0,0.5)中的频率为0.08×0.5=0.04,
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5)中的频率分别为0.08,0.20,0.26,0.06,0.04,0.02.
由0.04+0.08+0.5×a+0.20+0.26+0.5×a+0.06+0.04+0.02=1,
解得a=0.30.
(2)由(1),100位居民每人月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计全市30万居民中月均用水量不低于3吨的人数为
300 000×0.12="36" 000.
(3)因为前6组的频率之和为0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85,
而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85,
所以2.5≤x<3.
由0.3×(x–2.5)=0.85–0.73,
解得x=2.9.
所以,估计月用水量标准为2.9吨时,85%的居民每月的用水量不超过标准.
【考点】
频率分布直方图
【名师点睛】
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,考查学生的分析问题、解决问题的能力.在频率分布直方图中,第n个小矩形的面积就是相应组的频率,所有小矩形的面积之和为1,这是解题的关键,也是识图的基础.
19.(1)100;(2)32;(3)20%分位数为91;平均数为94.3;答案见解析.
【分析】
(1)求出频率,利用频率即可得解;
(2)利用百分位数的定义即可求解;
(3)利用百分位数的定义及平均数的定义计算可得解,再作出评价和感想.
【详解】
(1)第一组频率为0.01×5=0.05,所以.
(2)由题图可知年龄低于30岁的所占比例为,年龄低于35岁的所占比例为,
所以抽取的x人的年龄的分位数在内,
由,所以抽取的x人的年龄的分位数为32.
(3)把参赛的10人的成绩按从小到大的顺序排列:88,90,92,92,95,96,96,97,98,99,
计算,所以这10人成绩的分位数为,
这10人成绩的平均数为
评价:从百分位数和平均数来看,参赛人员的认知程度很高.
感想:结合本题和实际,符合社会主义核心价值观即可.
【点睛】
关键点点睛:本题考查频率,频数,总数的关系及第百分位数的计算,理解第百分位数的定义及应用是解题的关键,考查学生的计算能力,属于一般题.
20.(Ⅰ)8万人;(Ⅱ);(Ⅲ).
【详解】
试题分析:(I)根据直方图可得样本中类学生所占比例为,所以类学生所占比例为,再根据总人数可估计在该项测评中被评为类学生的人数;(Ⅱ)利用列举法列举出按要求分成两组,分组的方法数为种,其中“甲、乙两组各有名类学生”的方法共有种,由古典概型概率公式可得结果;(Ⅲ)根据直方图,结合表格数据可得结论.
试题解析:(1)依题意得,样本中类学生所占比例为,
所以类学生所占比例为. 因为全市高中学生共万人,
所以在该项测评中被评为类学生的人数约为8万人.
(2)由表1得,在5人(记为)中,类学生有2人(不妨设为).
将他们按要求分成两组,分组的方法数为种.
依次为: .
所以“甲、乙两组各有一名类学生”的概率为.
(3).
21.(1);(2);(3)有效,理由见解析.
【分析】
(1)设这名学生考核优秀为事件,利用古典概型的概率公式求解;
(2)设至少有一人考核成绩优秀为事件,再利用古典概型的概率公式求解;
(3)根据表格中的数据,满足的成绩有16个,即得解.
【详解】
(1)设这名学生考核优秀为事件,
由茎叶图中的数据可以知道,30名同学中,有7名同学考核优秀,
所以所求概率约为.
(2)设从图中考核成绩满足的学生中任取2人,
至少有一人考核成绩优秀为事件,因为表中成绩在的6人中有2个人考核为优,
所以基本事件空间包含15个基本事件,它们是
事件包含9个基本事件,它们是
所以.
(3)根据表格中的数据,满足的成绩有16个,
所以
所以可以认为此次冰雪培训活动有效.
【点睛】
本题主要考查茎叶图,考查古典概型的概率的计算,意在考查学生对这些知识的理解掌握水平.
北京·高一·
