2021秋北师版八上数学第七章平行线与相交线导学案(无答案)
文档属性
| 名称 | 2021秋北师版八上数学第七章平行线与相交线导学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 889.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-24 00:00:00 | ||
图片预览





文档简介
2021秋北师版八上数学第七章平行线与相交线导学案
7、1 为什么要证明
学习目标:
1.运用实验验证、举反例验证、推理论证等方法来验证某些问题的结论正确与否.
2.经历观察、验证、归纳等过程,培养推理意识.
3.知道检验数学结论的常用方法:实验验证、举出反例、推理论证等.
重点和难点:
运用实验验证、举反例验证、推理论证等方法来验证某些问题的结论正确与否
学习过程:
阅读教材P162-163并完成以下问题:
1.通过列表归纳,根据自己以往的经验判断,在=10以前都一直认为是一个质数,但当= ____ 时,找到了一个反例,进而发现不能根据少数几个现象轻易肯定某个数学结论的正确性.
2.设赤道周长为c,则赤道的半径为
铁丝围成的圆的半径为
所以铁丝与地球赤道之间的间隙为 :
结论:
3.归纳总结:
由以上可知:实验、观察、归纳得到的结论可能 也可能 。因此,要判断数学结论 ,仅仅依靠实验、观察、归纳是不够的,必须进行
二、合作探究学习
探究1:
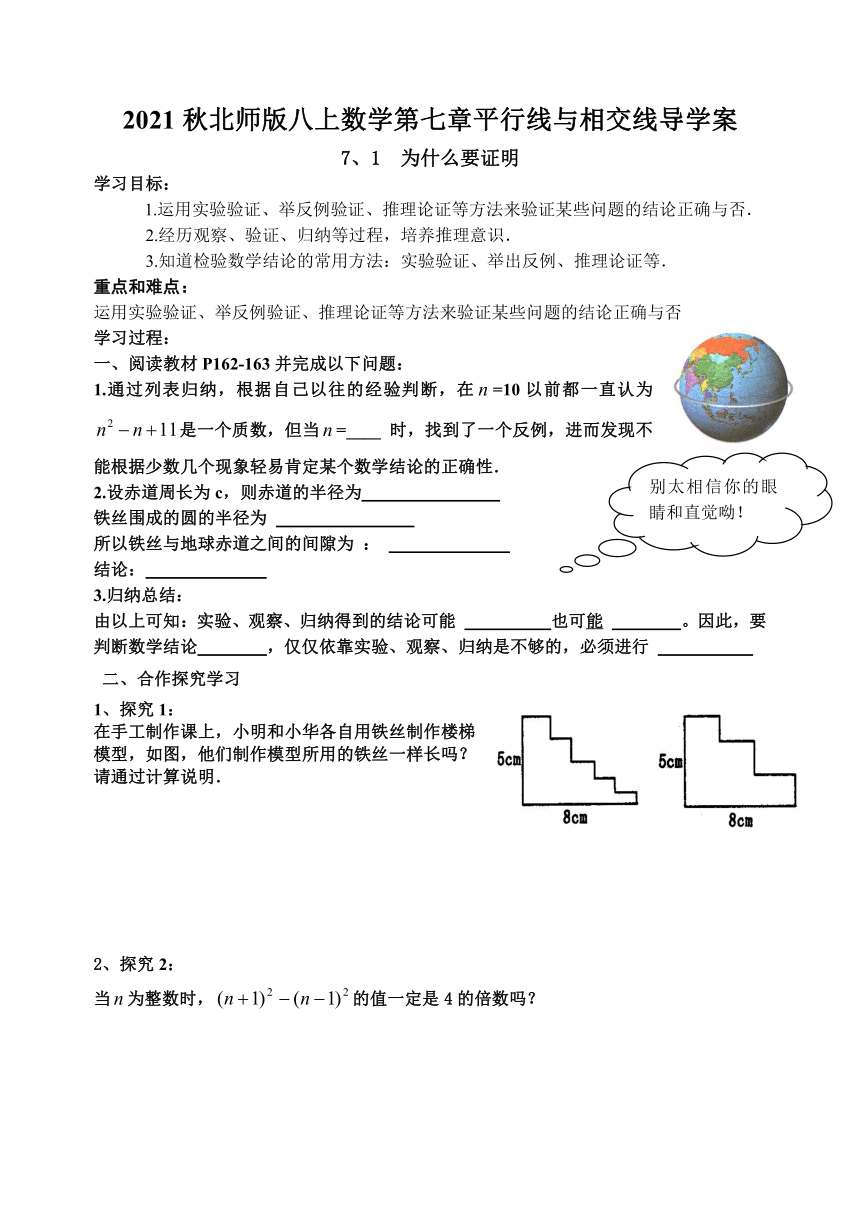
在手工制作课上,小明和小华各自用铁丝制作楼梯模型,如图,他们制作模型所用的铁丝一样长吗?请通过计算说明.
探究2:
当为整数时,的值一定是4的倍数吗?
3、探究3:
如图,DE⊥AC,DF⊥AB,你能判断∠CAB与∠EDF的大小关系吗?小明由此得出结论:如果两个角的两边分别垂直,那么这两个角互补。你认为正确吗?与同伴交流。
三、课堂检测:
1.下列正确的( )
A.如果为实数, 那么3>2 B. 若、b为实数 且2>b2 ,,则>b
C. 若为实数且≠0,则 D .若为不为0的实数, 则
教材163页随堂练习1题
3.当n为正整数时,n2+3n+1的值一定是质数吗?
4、如图所示,∠1=∠2,∠3=∠B,FG⊥AC于G,猜想CD与AB的关系,并证明你的猜想。
课堂小结:
这节课你学到了什么?你还有什么疑问?
课后作业:
1.教材164 习题7.1 1-3题
2.如图, AB∥CD,AD∥BC,DE∥BF,图中有多少对相等的同位角?
7.2定义与命题(1)
学习目标:
1.初步认识定义、命题、真命题、假命题的含义,会区分某些语句是不是命题.
2.会区分一个命题的条件和结论,了解判断命题真假的方法。
重点和难点:
对命题语句特征的判断
学习过程:
阅读教材165-166页完成下列问题:
1.定义就是对某个名称和术语的含义加以 ,作出 。
其形式为 × × × × × × 叫 × × ×
如:
2.判断一件事情的 ,叫做 。如果一个句子没有对某一件事情做出任何 ,那么它就不是 。
3.命题由 和 组成,通常可写成 “ ” 的形式;命题有真命题和假命题, 为真命题, 为假命题。
二、合作探究
1.探究1:
下列句子哪些是命题?
(1)动物都需要水; (2)猴子是动物的一种;
(3)玫瑰花是动物; (4美丽的天空;
(5相等的角是对顶角; (6)负数都小于零;
(7)你的作业做完了吗? (8)所有的质数都是奇数;
(9)过直线l外一点作l的平行线; (10)如果a=b,a=c,那么b=c;
2.探究2:
命题“全等三角形的面积相等”写成“如果······那么······”的形式是:
3.探究3:
指出下列命题的条件和结论并判断是真命题还是假命题?若是假命题请举出反例。
如果两个角的两边分别平行,那么这两个角相等
互补的两个角一定是一个锐角一个钝角
三、课堂检测:
1.下列是命题的是( )
A.画两条相等的线段 B.等于同一个角的两个角相等吗?
C.延长线段AO到C,使OC=OA D.两直线平行,内错角相等.
2. 指出下列各命题的条件和结论,并指出哪些是真命题,哪些是假命题,并通过反例来说明假命题。
(1)若∥,∥,则∥;
解:条件: ,结论: ,是 命题.
如果两个角互补,那么这两个角一定是邻补角;
解:条件: ,结论: ,是 命题.
绝对值相等的两个数一定相等.
解:条件: ,结论: ,是 命题.
教材页166页 随堂练习2题
4.把下列命题改写成“如果……,那么……”的形式:
(1)平行于同一条直线的两条直线平行;
(2)等角的补角相等;
四、课堂小结:
这节课你学到了什么?你还有什么疑问?
五、课后作业:
1.教材页167页 习题7.2 2-3题
2.举出反例说明下列命题是假命题.
(1)大于90°的角是钝角;
(2)如果一个角的两条边分别平行于另一个角的两条边,那么这两个角相等.
3.指出下列命题的条件和结论,并判断命题的真假.
(1)垂直于同一条直线的两条直线平行.
(2)同位角相等.
(3)若,则.
(4)两条直线相交只有一个交点.
7.2定义与命题(2)
学习目标:
1.初步认识公理、证明、定理的含义;
2.识记本教材所采用的公理;
3.初步体会证明的思路与书写的过程。
重点和难点:
识记本教材所采用的公理,初步体会证明的思路与书写的过程。
学习过程:
一、阅读教材168-170页,完成下列问题:
1.知识点:公理、证明、定理的含义
(1)公理:
(2)定理:
(3)证明:
2.识记本教材的八条公理:
①
②
③
④
⑤
⑥
⑦
⑧
3.公理的正确性 ,可以直接用来 ,
此外 也可看作公理.比如:如果a=b,b=c,那么a=c
4.证明一个命题的步骤有: (1) (2) 、(3) 。
二、合作探究:
已知:如图,直线AB与直线CD相交于点O,∠AOC与∠BOD是对顶角。
求证:∠AOC =∠BOD
证明:
三、课堂检测:
1.下列命题是假命题的是( )
A、如果∥b,b∥c,那么∥c B、锐角三角形中最大的角一定大于或等于60°
C、如果是有理数,那么是实数 D、两条直线被第三条直线所截,内错角相等
2.下列叙述错误的是( )
A、所有的命题都有条件和结论 B、所有的命题都是定理
C、所有的定理都是命题 D、所有的公理都是真命题
3.判断下列命题的真假:
(1)一个三角形如果有两个角互余,那么这个三角形是直角三角形;
(2)如果∣∣=∣∣,那么
4.证明给下列命题:全等三角形对应边上的中线相等。
5.教材170页 随堂练习
四、课堂小结:
这节课你学到了什么?你还有什么疑问?
五、课后作业:
1.教材171页 习题7.3 1、2 题
7.3平行线的判定
学习目标:1.熟练掌握平行线的判定公理及定理;
2.能对平行线的判定进行灵活运用,并把它们应用于几何证明中
重点和难点:
平行线的判定公理及定理及灵活运用
学习过程:
阅读教材172-173页,完成下列问题:
1.证明一个命题的步骤有:
(1) (2)
(3) 。
2.证明的语言必须 ,推理过程要有 .
3. 都可以作为证明的依据,用来证明的结论。
4.平行线判定的公理是:
5.平行线判定定理理有:
合作探究
1.探究1:
如图AB∥CD ∠1=∠2,∠3=∠4,
求证:AD∥BE
证明:∵AB∥CD(已知)
∴∠4=∠_____( )
∵∠3=∠4(已知)
∴∠3=∠_____( )
∵∠1=∠2(已知)
∴∠ 1+∠CAF=∠2+∠CAF( )
即 ∠_____ =∠_____( )
∴∠3=∠_____
∴AD∥BE( )
2.探究2:
已知:如图,DG∥AB,∠1 =∠2,求证:E∥BD
三、课堂检测
1.如图7-3-1,下列条件不能判定直线∥的是( )
A.∠1=∠2 B.∠1=∠3 C.∠1+∠3=180° D.∠2+∠4=180°
2.如图7-3-2,能判断EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABE
3.教材173页 随堂练习
如图,∠1=∠2,∠3=∠4,求证:EF∥GH
四、课堂小结:
这节课你学到了什么?你还有什么疑问?
五、课后作业:
1.教材173页 习题7.4 1、2题
2.已知:如图、BE//CF,BE、CF分别平分∠ABC和∠BCD
求证:AB//CD
7.4平行线性质定理
学习目标
1.认识平行线的三条性质.
2.能熟练证明这三条性质证明几何题.
重点和难点:
证明的步骤和格式;正确对照命题画出图形.写出已知、求证.
学习过程:
一、阅读教材175-176页的内容,请回答以下问题:
1.平行线的性质定理有哪些?
(1)两直线平行, 相等.符号语言: ∵∥b(已知),∴______=______(两直线平行, 相等)
(2)两直线平行, 相等.符号语言: ∵∥b(已知),∴______=______(两直线平行, 相等)
(3)两直线平行, 互补.符号语言:∵∥b(已知),∴ (两直线平行, 互补)
2.定理:平行于同一条直线的两条直线 .符号语言:∵∥b,∥c ∴
二、合作探究学习
1.探究1:
证明:(定理)两条平行线被第三条直线所截,内错角相等
你能根据所作的图形写出已知、求证吗?
已知:如图,
求证:
证明: ∵______∥______(已知),
∴_______=________(两条直线平行,同位角相等)
∵________=________(对顶角相等),
∴________=_________(等量代换).
小结:定理:两条平行线被第三条直线所截,内错角相等,简写为:_________________________,
2.探究2:
证明:定理:两条平行线被第三条直线所截,同旁内角_______.
你能根据所作的图形写出已知、求证吗?
已知:如图,
求证:
证明:∵_____∥______ (_________)
∴∠1=∠2 (_______________________)
∵______+______=180°(邻补角定义)
∴______+______=_______°(等量代换)
小结:定理:两条平行线被第三条直线所截,同旁内角__________,简写为:两直线平行,________________
3.探究3:平行线判定定理与性质定理的关系.
如图∵∠1=∠2
∴___∥____( )
∴∠A=_____ ( )
又∵∠A=∠3 (已知)
∴∠___=∠___ ( )
∴ ___∥____ ( )
小结:1.两直线平行的判定与性质:
2.命题证明的主要步骤:(1)理清题意;(2)根据题意正确画出图形;(3)根据题意写出“已知”和“求证”
(4)分析题意,探索证明的思路;(5)写出证明过程;(6)检查
三、当堂检测:
1.如图,AB∥CD, ∠1=110°, ∠ECD=70°, ∠E=( )
A. 30° B. 40° C. 50° D. 60°
2.如图,下列推理正确的是( )
A. ∵MA∥NB, ∴∠1=∠3 B. ∵∠2=∠4, ∴MC∥ND
C. ∵∠1=∠3, ∴MA∥NB D. ∵MC∥ND, ∴∠1=∠3
3.根据图形回答问题: 已知平行线AB、CD被直线AE所截
(1)若∠1=110°,那么∠2= .理由:
(2)若∠1=110°,那么∠3= .理由:
(3)若∠1=110°,那么∠4= .理由:
4如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=50°,求∠2的度数
5.已知,如图,AB∥CD,求证:∠AEC=∠A+∠C.
四、课堂小结:
平行线的性质与判定有哪些?证明题的一般步骤有哪些?
课后作业:
1.教材177页 习题7.5 1-4题
2.已知:如图,∠ADE=∠B,∠1=∠2,FG⊥AB,求证:CD⊥AB
3.已知,如图,AB∥EF.(虚线为提示辅助线)
求证:当点C在直线BF的左,右侧时∠BCF=∠B+∠F
7.5三角形内角和定理的证明(1)
学习目标
1.能够证明三角形内角和定理及简单应用.
2.灵活证明三角形内角和定理解决相关问题.
重点和难点
三角形内角和定理的证明及灵活应用于解决相关问题.
学习过程
一、阅读教材178-179页的内容,请回答以下问题
1.任何一个三角形都有 个内角,并且每一个内角均 0°且 180°.
2.三角形根据最大内角的度数,可以分为 三角形, 三角形和 三角形.
三角形内角和定理是 .
试一试:△ABC中,若∠C=90°,∠A=30°,∠B=_____;若∠A=50°,∠B=∠C,则△ABC中∠B=_______.
二、合作探究学习
1.探究1:
用严谨的证明来论证三角形内角和定理.
已知△ABC,求证∠A+∠B+∠C=180°
方法一: 方法二:
2.探究2:三角形内角和定理的运用
如图在△ABC中,∠B=38°, ∠C=62°AD是△ABC的角平分线,求∠ADB的度数.
三、当堂检测:
1.△ABC中,若∠C=90°,∠A=27°,∠B=_______;
2.一个三角形三个内角之比为2∶3∶7,这个三角形是( )
A.直角三角形 B.等腰三角形 C.锐角三角形 D.钝角三角形
3.教材179页 随堂练习 1-3题
4.已知:△ABC中,∠C=∠B=2∠A.
(1)求∠B的度数;
(2)若BD是AC边上的高,求∠DBC的度数.
四、课堂小结
三角形内角和等于多少度?
课后作业
1.教材180页 习题7.6 1-4题
2.三角形的三个内角中,只能有____个直角或____个钝角.任何一个三角形中,至少有____个锐角;至多有____个锐角.
3.已知:AB∥CD,EG平分∠BEF,FG平分∠EFD.求证:EG⊥FG.
4.(选做)如图,△ABC中,BO,CO平分∠ABC和∠ACB.
(1)若∠A=120°,求∠BOC的度数;
(2)若∠A=,试探究∠BOC与的关系.
7.5三角形内角和定理的证明(2)
学习目标
1.能认识三角形外角的两条性质;
2.灵活证明三角形的外角和两条性质解决相关问题.
重点和难点
灵活证明三角形的外角和两条性质解决相关问题.
学习过程
一、阅读教材181-182页的内容,请回答以下问题
1.什么是三角形的外角
三角形的一边与 所组成的角,叫做三角形的外角.
外角的特征有三:
(1)顶点在 上.
(2)一条边是三角形的 .
(3)另一条边是三角形某条边的 .
三角形的外角有什么性质定理
定理1:三角形的一个外角等于 两个内角的和.
定理2:三角形的一个外角 任何一个和它不相邻的内角.
试一试:如图, 是△ABC的外角,∠ACD ∠A(填“>”、“<”或“=”).若∠A=60°,∠B=65°,∠ACD=_____°.
什么是推论
由一个基本事实或定理 的定理,叫做这个基本事实或定理的推论.推论可当作 使用.
二、合作探究学习
1.探究1:
问题1:如图,△ABC中,∠A=70°,∠B=60°,∠ACD是△ABC的一个外角,求证:∠ACD=∠A+∠B
问题2:任意一个△ABC的一个外角∠ACD, 求证:∠ACD>∠A
探究2:
例1:已知:如图,在△ABC中,∠B=∠C,AD平分外角∠EAC.
求证:AD∥BC
思考:你还有其他证明方法?
探究3:
例2:已知:如图,P是△ABC内一点,连接PB,PC.
求证:∠BPC > ∠A
思考:你还有其他证明方法?
三、当堂检测:
1.如图,下列哪些说法一定正确
A.∠HEC >∠B B.∠B+∠ACB=180°—∠A
C.∠B+∠ACB<180° D.∠B>∠ACD
2.已知如图,∥,则下列式子中值为180°的是( )
A. ∠1+∠2+∠3 B. ∠1+∠2-∠3 C. ∠2+∠3 -∠1 D. ∠1-∠2+∠3
3.如图已知,AC=CD,AE=BE, ∠CFE=117°,则∠A的度数是 °
4.教材183页 随堂练习1、2题
四、课堂小结
三角形内角和等于多少度?
课后作业
1.教材183页 习题7.7 1-4题
2.如图,已知BE、CE分别是△ABC的内角、外角的平分线,∠A=40°,求∠E= °.
3.已知:如图,D是AB上一点,E是AC上的一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:
(1)∠BDC的度数;
(2)∠BFD的度数.
回顾与思考
学习目标:
1.知道命题的概念与命题的构成;
2.熟悉平行线的性质定理与判定定理,三角形内角和定理及三角形的外角的性质等概念.
重点与难点:灵活用平行线的性质定理与判定定理、三角形内角和定理及三角形的外角的性质等进行证明.
学习过程:
一、知识回顾
1.命题
(1)______________________,叫命题,_______的命题是真命题,不正确的命题是___________.
(2)公认的真命题称为____________,经过证明的真命题称为_____________.
2.平行线的判定
平行线的判定:公理:____________相等,两直线平行.
判定定理1:___________相等,两直线平行.
判定定理2:_______________,两直线平行.
定理:平行于同一直线的两直线___________.
3.平行线的性质
性质定理1:两直线平行,同位角___________. 性质定理2:两直线平行,内错角_________.
性质定理3:两直线平行,同旁内角__________.
4.三角形的判定
(1)三角形内角和定理:三角形的内角和等于__________.
(2) 定理:三角形的一个外角等于和它不相邻的____________________.
(3) 定理:三角形的一个外角大于任何一个和它____________________.
二、当堂检测
1.下列语句是命题的有( )
A.两点之间线段最短 B.向雷锋同志学习 C.对顶角相等; D.花儿在春天开放
2.下列命题,哪些是真命题?哪些是假命题?如果是真命题,请写出条件与结论,如果是假命题,请举出反例.
(1)同角的补角相等;(2)同位角相等,两直线平行;(3)若|a|=|b|,则a=b.
3.如图,AD、BE、CF为△ABC的三条角平分线,则:∠1+∠2+∠3=________.
4.如图所示,△ABC中,∠ACD=115°,∠B=55°, 则∠A= , ∠ACB=
5.已知,如图,AB∥CD,若∠ABE=130°, ∠CDE=152°,则∠ BED=__________.
第3题图 第4题图 第5题图
6.教材184页复习题 1-6题.小组派代表展示讲解.
7.已知,如图,直线AB∥ED. 求证:∠ABC+∠CDE=∠BCD.
三、课后作业:
1.如图,△ABC中,∠B=55°,∠C=63°,DE∥AB,则∠DEC为( )
A.63° B. 62° C. 55° D.118°
2.命题“垂直于同一条直线的两条直线互相平行”的题设是( )
A.垂直 B.两条直线 C.同一条直线 D.两条直线垂 直于同一条直线
3.如图,BD平分∠ABC,若∠1=∠2,则 ( )
A.AB∥CD B. AD∥BC C. AD=BC D.AB=CD
4.三角形的一个外角是锐角,则此三角形的形状是 三角形
5.如图∠A=65 ,∠ABD=∠BCE=30 ,且CE平分∠ACB,求∠BEC.
6.如图,AD⊥BC,EF⊥BC,∠3=∠C.
求证:∠1=∠2.
别太相信你的眼睛和直觉呦!
图7-3-1
图7-3-2
D
C
A
B
C
A
B
C
第3题图
第2题图
(1) (2)
A
B
G
D
F
C
E
1
3
2
7、1 为什么要证明
学习目标:
1.运用实验验证、举反例验证、推理论证等方法来验证某些问题的结论正确与否.
2.经历观察、验证、归纳等过程,培养推理意识.
3.知道检验数学结论的常用方法:实验验证、举出反例、推理论证等.
重点和难点:
运用实验验证、举反例验证、推理论证等方法来验证某些问题的结论正确与否
学习过程:
阅读教材P162-163并完成以下问题:
1.通过列表归纳,根据自己以往的经验判断,在=10以前都一直认为是一个质数,但当= ____ 时,找到了一个反例,进而发现不能根据少数几个现象轻易肯定某个数学结论的正确性.
2.设赤道周长为c,则赤道的半径为
铁丝围成的圆的半径为
所以铁丝与地球赤道之间的间隙为 :
结论:
3.归纳总结:
由以上可知:实验、观察、归纳得到的结论可能 也可能 。因此,要判断数学结论 ,仅仅依靠实验、观察、归纳是不够的,必须进行
二、合作探究学习
探究1:
在手工制作课上,小明和小华各自用铁丝制作楼梯模型,如图,他们制作模型所用的铁丝一样长吗?请通过计算说明.
探究2:
当为整数时,的值一定是4的倍数吗?
3、探究3:
如图,DE⊥AC,DF⊥AB,你能判断∠CAB与∠EDF的大小关系吗?小明由此得出结论:如果两个角的两边分别垂直,那么这两个角互补。你认为正确吗?与同伴交流。
三、课堂检测:
1.下列正确的( )
A.如果为实数, 那么3>2 B. 若、b为实数 且2>b2 ,,则>b
C. 若为实数且≠0,则 D .若为不为0的实数, 则
教材163页随堂练习1题
3.当n为正整数时,n2+3n+1的值一定是质数吗?
4、如图所示,∠1=∠2,∠3=∠B,FG⊥AC于G,猜想CD与AB的关系,并证明你的猜想。
课堂小结:
这节课你学到了什么?你还有什么疑问?
课后作业:
1.教材164 习题7.1 1-3题
2.如图, AB∥CD,AD∥BC,DE∥BF,图中有多少对相等的同位角?
7.2定义与命题(1)
学习目标:
1.初步认识定义、命题、真命题、假命题的含义,会区分某些语句是不是命题.
2.会区分一个命题的条件和结论,了解判断命题真假的方法。
重点和难点:
对命题语句特征的判断
学习过程:
阅读教材165-166页完成下列问题:
1.定义就是对某个名称和术语的含义加以 ,作出 。
其形式为 × × × × × × 叫 × × ×
如:
2.判断一件事情的 ,叫做 。如果一个句子没有对某一件事情做出任何 ,那么它就不是 。
3.命题由 和 组成,通常可写成 “ ” 的形式;命题有真命题和假命题, 为真命题, 为假命题。
二、合作探究
1.探究1:
下列句子哪些是命题?
(1)动物都需要水; (2)猴子是动物的一种;
(3)玫瑰花是动物; (4美丽的天空;
(5相等的角是对顶角; (6)负数都小于零;
(7)你的作业做完了吗? (8)所有的质数都是奇数;
(9)过直线l外一点作l的平行线; (10)如果a=b,a=c,那么b=c;
2.探究2:
命题“全等三角形的面积相等”写成“如果······那么······”的形式是:
3.探究3:
指出下列命题的条件和结论并判断是真命题还是假命题?若是假命题请举出反例。
如果两个角的两边分别平行,那么这两个角相等
互补的两个角一定是一个锐角一个钝角
三、课堂检测:
1.下列是命题的是( )
A.画两条相等的线段 B.等于同一个角的两个角相等吗?
C.延长线段AO到C,使OC=OA D.两直线平行,内错角相等.
2. 指出下列各命题的条件和结论,并指出哪些是真命题,哪些是假命题,并通过反例来说明假命题。
(1)若∥,∥,则∥;
解:条件: ,结论: ,是 命题.
如果两个角互补,那么这两个角一定是邻补角;
解:条件: ,结论: ,是 命题.
绝对值相等的两个数一定相等.
解:条件: ,结论: ,是 命题.
教材页166页 随堂练习2题
4.把下列命题改写成“如果……,那么……”的形式:
(1)平行于同一条直线的两条直线平行;
(2)等角的补角相等;
四、课堂小结:
这节课你学到了什么?你还有什么疑问?
五、课后作业:
1.教材页167页 习题7.2 2-3题
2.举出反例说明下列命题是假命题.
(1)大于90°的角是钝角;
(2)如果一个角的两条边分别平行于另一个角的两条边,那么这两个角相等.
3.指出下列命题的条件和结论,并判断命题的真假.
(1)垂直于同一条直线的两条直线平行.
(2)同位角相等.
(3)若,则.
(4)两条直线相交只有一个交点.
7.2定义与命题(2)
学习目标:
1.初步认识公理、证明、定理的含义;
2.识记本教材所采用的公理;
3.初步体会证明的思路与书写的过程。
重点和难点:
识记本教材所采用的公理,初步体会证明的思路与书写的过程。
学习过程:
一、阅读教材168-170页,完成下列问题:
1.知识点:公理、证明、定理的含义
(1)公理:
(2)定理:
(3)证明:
2.识记本教材的八条公理:
①
②
③
④
⑤
⑥
⑦
⑧
3.公理的正确性 ,可以直接用来 ,
此外 也可看作公理.比如:如果a=b,b=c,那么a=c
4.证明一个命题的步骤有: (1) (2) 、(3) 。
二、合作探究:
已知:如图,直线AB与直线CD相交于点O,∠AOC与∠BOD是对顶角。
求证:∠AOC =∠BOD
证明:
三、课堂检测:
1.下列命题是假命题的是( )
A、如果∥b,b∥c,那么∥c B、锐角三角形中最大的角一定大于或等于60°
C、如果是有理数,那么是实数 D、两条直线被第三条直线所截,内错角相等
2.下列叙述错误的是( )
A、所有的命题都有条件和结论 B、所有的命题都是定理
C、所有的定理都是命题 D、所有的公理都是真命题
3.判断下列命题的真假:
(1)一个三角形如果有两个角互余,那么这个三角形是直角三角形;
(2)如果∣∣=∣∣,那么
4.证明给下列命题:全等三角形对应边上的中线相等。
5.教材170页 随堂练习
四、课堂小结:
这节课你学到了什么?你还有什么疑问?
五、课后作业:
1.教材171页 习题7.3 1、2 题
7.3平行线的判定
学习目标:1.熟练掌握平行线的判定公理及定理;
2.能对平行线的判定进行灵活运用,并把它们应用于几何证明中
重点和难点:
平行线的判定公理及定理及灵活运用
学习过程:
阅读教材172-173页,完成下列问题:
1.证明一个命题的步骤有:
(1) (2)
(3) 。
2.证明的语言必须 ,推理过程要有 .
3. 都可以作为证明的依据,用来证明的结论。
4.平行线判定的公理是:
5.平行线判定定理理有:
合作探究
1.探究1:
如图AB∥CD ∠1=∠2,∠3=∠4,
求证:AD∥BE
证明:∵AB∥CD(已知)
∴∠4=∠_____( )
∵∠3=∠4(已知)
∴∠3=∠_____( )
∵∠1=∠2(已知)
∴∠ 1+∠CAF=∠2+∠CAF( )
即 ∠_____ =∠_____( )
∴∠3=∠_____
∴AD∥BE( )
2.探究2:
已知:如图,DG∥AB,∠1 =∠2,求证:E∥BD
三、课堂检测
1.如图7-3-1,下列条件不能判定直线∥的是( )
A.∠1=∠2 B.∠1=∠3 C.∠1+∠3=180° D.∠2+∠4=180°
2.如图7-3-2,能判断EB∥AC的条件是( )
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABE
3.教材173页 随堂练习
如图,∠1=∠2,∠3=∠4,求证:EF∥GH
四、课堂小结:
这节课你学到了什么?你还有什么疑问?
五、课后作业:
1.教材173页 习题7.4 1、2题
2.已知:如图、BE//CF,BE、CF分别平分∠ABC和∠BCD
求证:AB//CD
7.4平行线性质定理
学习目标
1.认识平行线的三条性质.
2.能熟练证明这三条性质证明几何题.
重点和难点:
证明的步骤和格式;正确对照命题画出图形.写出已知、求证.
学习过程:
一、阅读教材175-176页的内容,请回答以下问题:
1.平行线的性质定理有哪些?
(1)两直线平行, 相等.符号语言: ∵∥b(已知),∴______=______(两直线平行, 相等)
(2)两直线平行, 相等.符号语言: ∵∥b(已知),∴______=______(两直线平行, 相等)
(3)两直线平行, 互补.符号语言:∵∥b(已知),∴ (两直线平行, 互补)
2.定理:平行于同一条直线的两条直线 .符号语言:∵∥b,∥c ∴
二、合作探究学习
1.探究1:
证明:(定理)两条平行线被第三条直线所截,内错角相等
你能根据所作的图形写出已知、求证吗?
已知:如图,
求证:
证明: ∵______∥______(已知),
∴_______=________(两条直线平行,同位角相等)
∵________=________(对顶角相等),
∴________=_________(等量代换).
小结:定理:两条平行线被第三条直线所截,内错角相等,简写为:_________________________,
2.探究2:
证明:定理:两条平行线被第三条直线所截,同旁内角_______.
你能根据所作的图形写出已知、求证吗?
已知:如图,
求证:
证明:∵_____∥______ (_________)
∴∠1=∠2 (_______________________)
∵______+______=180°(邻补角定义)
∴______+______=_______°(等量代换)
小结:定理:两条平行线被第三条直线所截,同旁内角__________,简写为:两直线平行,________________
3.探究3:平行线判定定理与性质定理的关系.
如图∵∠1=∠2
∴___∥____( )
∴∠A=_____ ( )
又∵∠A=∠3 (已知)
∴∠___=∠___ ( )
∴ ___∥____ ( )
小结:1.两直线平行的判定与性质:
2.命题证明的主要步骤:(1)理清题意;(2)根据题意正确画出图形;(3)根据题意写出“已知”和“求证”
(4)分析题意,探索证明的思路;(5)写出证明过程;(6)检查
三、当堂检测:
1.如图,AB∥CD, ∠1=110°, ∠ECD=70°, ∠E=( )
A. 30° B. 40° C. 50° D. 60°
2.如图,下列推理正确的是( )
A. ∵MA∥NB, ∴∠1=∠3 B. ∵∠2=∠4, ∴MC∥ND
C. ∵∠1=∠3, ∴MA∥NB D. ∵MC∥ND, ∴∠1=∠3
3.根据图形回答问题: 已知平行线AB、CD被直线AE所截
(1)若∠1=110°,那么∠2= .理由:
(2)若∠1=110°,那么∠3= .理由:
(3)若∠1=110°,那么∠4= .理由:
4如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=50°,求∠2的度数
5.已知,如图,AB∥CD,求证:∠AEC=∠A+∠C.
四、课堂小结:
平行线的性质与判定有哪些?证明题的一般步骤有哪些?
课后作业:
1.教材177页 习题7.5 1-4题
2.已知:如图,∠ADE=∠B,∠1=∠2,FG⊥AB,求证:CD⊥AB
3.已知,如图,AB∥EF.(虚线为提示辅助线)
求证:当点C在直线BF的左,右侧时∠BCF=∠B+∠F
7.5三角形内角和定理的证明(1)
学习目标
1.能够证明三角形内角和定理及简单应用.
2.灵活证明三角形内角和定理解决相关问题.
重点和难点
三角形内角和定理的证明及灵活应用于解决相关问题.
学习过程
一、阅读教材178-179页的内容,请回答以下问题
1.任何一个三角形都有 个内角,并且每一个内角均 0°且 180°.
2.三角形根据最大内角的度数,可以分为 三角形, 三角形和 三角形.
三角形内角和定理是 .
试一试:△ABC中,若∠C=90°,∠A=30°,∠B=_____;若∠A=50°,∠B=∠C,则△ABC中∠B=_______.
二、合作探究学习
1.探究1:
用严谨的证明来论证三角形内角和定理.
已知△ABC,求证∠A+∠B+∠C=180°
方法一: 方法二:
2.探究2:三角形内角和定理的运用
如图在△ABC中,∠B=38°, ∠C=62°AD是△ABC的角平分线,求∠ADB的度数.
三、当堂检测:
1.△ABC中,若∠C=90°,∠A=27°,∠B=_______;
2.一个三角形三个内角之比为2∶3∶7,这个三角形是( )
A.直角三角形 B.等腰三角形 C.锐角三角形 D.钝角三角形
3.教材179页 随堂练习 1-3题
4.已知:△ABC中,∠C=∠B=2∠A.
(1)求∠B的度数;
(2)若BD是AC边上的高,求∠DBC的度数.
四、课堂小结
三角形内角和等于多少度?
课后作业
1.教材180页 习题7.6 1-4题
2.三角形的三个内角中,只能有____个直角或____个钝角.任何一个三角形中,至少有____个锐角;至多有____个锐角.
3.已知:AB∥CD,EG平分∠BEF,FG平分∠EFD.求证:EG⊥FG.
4.(选做)如图,△ABC中,BO,CO平分∠ABC和∠ACB.
(1)若∠A=120°,求∠BOC的度数;
(2)若∠A=,试探究∠BOC与的关系.
7.5三角形内角和定理的证明(2)
学习目标
1.能认识三角形外角的两条性质;
2.灵活证明三角形的外角和两条性质解决相关问题.
重点和难点
灵活证明三角形的外角和两条性质解决相关问题.
学习过程
一、阅读教材181-182页的内容,请回答以下问题
1.什么是三角形的外角
三角形的一边与 所组成的角,叫做三角形的外角.
外角的特征有三:
(1)顶点在 上.
(2)一条边是三角形的 .
(3)另一条边是三角形某条边的 .
三角形的外角有什么性质定理
定理1:三角形的一个外角等于 两个内角的和.
定理2:三角形的一个外角 任何一个和它不相邻的内角.
试一试:如图, 是△ABC的外角,∠ACD ∠A(填“>”、“<”或“=”).若∠A=60°,∠B=65°,∠ACD=_____°.
什么是推论
由一个基本事实或定理 的定理,叫做这个基本事实或定理的推论.推论可当作 使用.
二、合作探究学习
1.探究1:
问题1:如图,△ABC中,∠A=70°,∠B=60°,∠ACD是△ABC的一个外角,求证:∠ACD=∠A+∠B
问题2:任意一个△ABC的一个外角∠ACD, 求证:∠ACD>∠A
探究2:
例1:已知:如图,在△ABC中,∠B=∠C,AD平分外角∠EAC.
求证:AD∥BC
思考:你还有其他证明方法?
探究3:
例2:已知:如图,P是△ABC内一点,连接PB,PC.
求证:∠BPC > ∠A
思考:你还有其他证明方法?
三、当堂检测:
1.如图,下列哪些说法一定正确
A.∠HEC >∠B B.∠B+∠ACB=180°—∠A
C.∠B+∠ACB<180° D.∠B>∠ACD
2.已知如图,∥,则下列式子中值为180°的是( )
A. ∠1+∠2+∠3 B. ∠1+∠2-∠3 C. ∠2+∠3 -∠1 D. ∠1-∠2+∠3
3.如图已知,AC=CD,AE=BE, ∠CFE=117°,则∠A的度数是 °
4.教材183页 随堂练习1、2题
四、课堂小结
三角形内角和等于多少度?
课后作业
1.教材183页 习题7.7 1-4题
2.如图,已知BE、CE分别是△ABC的内角、外角的平分线,∠A=40°,求∠E= °.
3.已知:如图,D是AB上一点,E是AC上的一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:
(1)∠BDC的度数;
(2)∠BFD的度数.
回顾与思考
学习目标:
1.知道命题的概念与命题的构成;
2.熟悉平行线的性质定理与判定定理,三角形内角和定理及三角形的外角的性质等概念.
重点与难点:灵活用平行线的性质定理与判定定理、三角形内角和定理及三角形的外角的性质等进行证明.
学习过程:
一、知识回顾
1.命题
(1)______________________,叫命题,_______的命题是真命题,不正确的命题是___________.
(2)公认的真命题称为____________,经过证明的真命题称为_____________.
2.平行线的判定
平行线的判定:公理:____________相等,两直线平行.
判定定理1:___________相等,两直线平行.
判定定理2:_______________,两直线平行.
定理:平行于同一直线的两直线___________.
3.平行线的性质
性质定理1:两直线平行,同位角___________. 性质定理2:两直线平行,内错角_________.
性质定理3:两直线平行,同旁内角__________.
4.三角形的判定
(1)三角形内角和定理:三角形的内角和等于__________.
(2) 定理:三角形的一个外角等于和它不相邻的____________________.
(3) 定理:三角形的一个外角大于任何一个和它____________________.
二、当堂检测
1.下列语句是命题的有( )
A.两点之间线段最短 B.向雷锋同志学习 C.对顶角相等; D.花儿在春天开放
2.下列命题,哪些是真命题?哪些是假命题?如果是真命题,请写出条件与结论,如果是假命题,请举出反例.
(1)同角的补角相等;(2)同位角相等,两直线平行;(3)若|a|=|b|,则a=b.
3.如图,AD、BE、CF为△ABC的三条角平分线,则:∠1+∠2+∠3=________.
4.如图所示,△ABC中,∠ACD=115°,∠B=55°, 则∠A= , ∠ACB=
5.已知,如图,AB∥CD,若∠ABE=130°, ∠CDE=152°,则∠ BED=__________.
第3题图 第4题图 第5题图
6.教材184页复习题 1-6题.小组派代表展示讲解.
7.已知,如图,直线AB∥ED. 求证:∠ABC+∠CDE=∠BCD.
三、课后作业:
1.如图,△ABC中,∠B=55°,∠C=63°,DE∥AB,则∠DEC为( )
A.63° B. 62° C. 55° D.118°
2.命题“垂直于同一条直线的两条直线互相平行”的题设是( )
A.垂直 B.两条直线 C.同一条直线 D.两条直线垂 直于同一条直线
3.如图,BD平分∠ABC,若∠1=∠2,则 ( )
A.AB∥CD B. AD∥BC C. AD=BC D.AB=CD
4.三角形的一个外角是锐角,则此三角形的形状是 三角形
5.如图∠A=65 ,∠ABD=∠BCE=30 ,且CE平分∠ACB,求∠BEC.
6.如图,AD⊥BC,EF⊥BC,∠3=∠C.
求证:∠1=∠2.
别太相信你的眼睛和直觉呦!
图7-3-1
图7-3-2
D
C
A
B
C
A
B
C
第3题图
第2题图
(1) (2)
A
B
G
D
F
C
E
1
3
2
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
