苏科版八年级数学上册 6.4 用一次函数解决问题教案
文档属性
| 名称 | 苏科版八年级数学上册 6.4 用一次函数解决问题教案 | 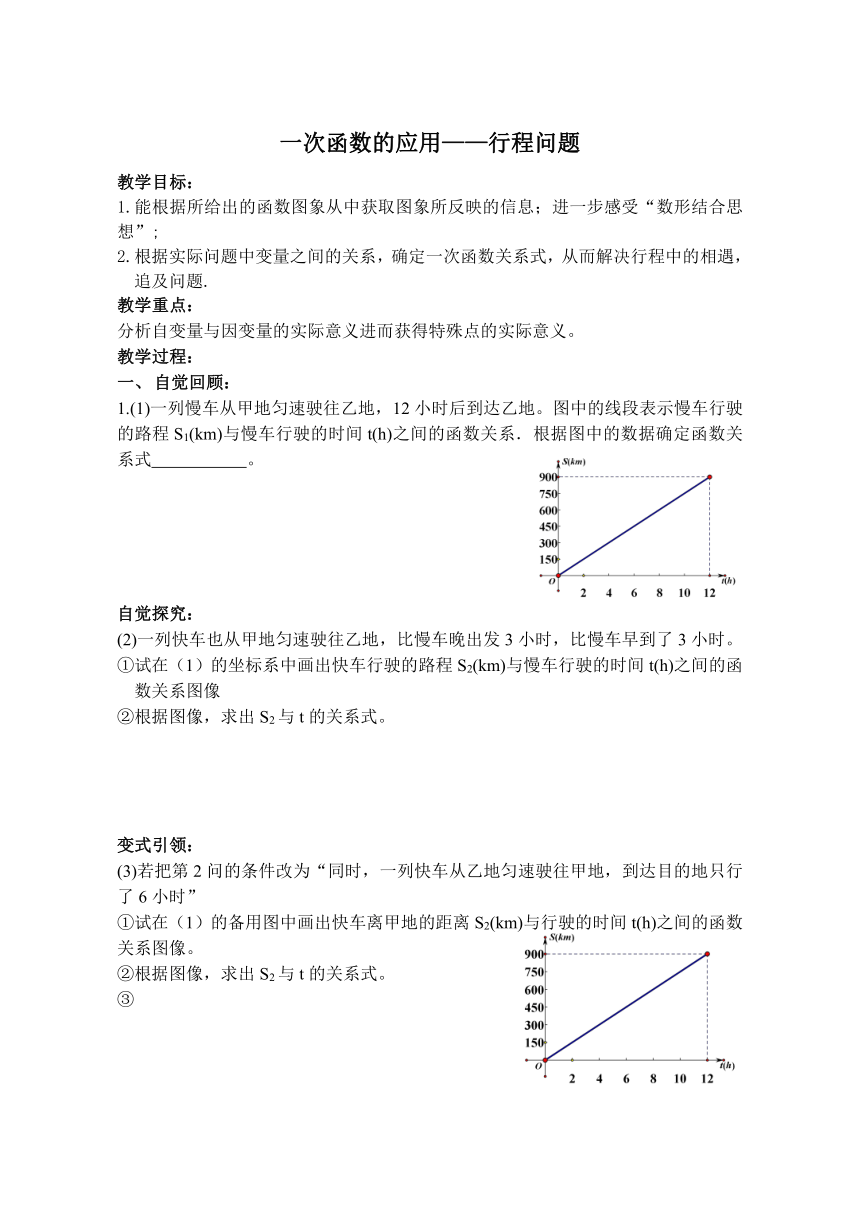 | |
| 格式 | docx | ||
| 文件大小 | 31.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-29 12:15:47 | ||
图片预览

文档简介
一次函数的应用——行程问题
教学目标:
1.能根据所给出的函数图象从中获取图象所反映的信息;进一步感受“数形结合思想”;
2.根据实际问题中变量之间的关系,确定一次函数关系式,从而解决行程中的相遇,追及问题.
教学重点:
分析自变量与因变量的实际意义进而获得特殊点的实际意义。
教学过程:
自觉回顾:
1.(1)一列慢车从甲地匀速驶往乙地,12小时后到达乙地。图中的线段表示慢车行驶的路程S1(km)与慢车行驶的时间t(h)之间的函数关系.根据图中的数据确定函数关系式 。
自觉探究:
(2)一列快车也从甲地匀速驶往乙地,比慢车晚出发3小时,比慢车早到了3小时。
①试在(1)的坐标系中画出快车行驶的路程S2(km)与慢车行驶的时间t(h)之间的函数关系图像
②根据图像,求出S2与t的关系式。
变式引领:
(3)若把第2问的条件改为“同时,一列快车从乙地匀速驶往甲地,到达目的地只行了6小时”
①试在(1)的备用图中画出快车离甲地的距离S2(km)与行驶的时间t(h)之间的函数关系图像。
②根据图像,求出S2与t的关系式。
③
二、自觉内化
2.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设慢车行驶的时间为t(h),两车之间的距离为d(km),图中的折线表示d与t之间的函数关系.根据图象进行以下探究:
(1)请解释图中A、B、C、D 点的实际意义;即甲、乙两地的距离为 km;
(2)慢车和快车的速度和为 ;
(3)慢车的速度为 ;
(4)快车的速度为 ;
(5)求C点坐标.
(6)快车出发多长时间后,两车相距150km
三、学有所悟
通过本节课的学习,不仅感受一次函数在我们解决实际问题,特别是行程问题中更显出其直观性、优越性,使我们进一步理解了数形结合思想在数学应用中的广泛性、重要性。
四、学以致用:
小聪和小明沿同一条路同时从学校出发到常州图书馆借阅资料,学校与图书馆的路程是4千米,小明步行,小聪骑自行车。小聪15分钟到达图书馆,借阅资料花了15分钟,当小聪按原速从原路回到学校时,小明刚好到达图书馆,
问:当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
教学目标:
1.能根据所给出的函数图象从中获取图象所反映的信息;进一步感受“数形结合思想”;
2.根据实际问题中变量之间的关系,确定一次函数关系式,从而解决行程中的相遇,追及问题.
教学重点:
分析自变量与因变量的实际意义进而获得特殊点的实际意义。
教学过程:
自觉回顾:
1.(1)一列慢车从甲地匀速驶往乙地,12小时后到达乙地。图中的线段表示慢车行驶的路程S1(km)与慢车行驶的时间t(h)之间的函数关系.根据图中的数据确定函数关系式 。
自觉探究:
(2)一列快车也从甲地匀速驶往乙地,比慢车晚出发3小时,比慢车早到了3小时。
①试在(1)的坐标系中画出快车行驶的路程S2(km)与慢车行驶的时间t(h)之间的函数关系图像
②根据图像,求出S2与t的关系式。
变式引领:
(3)若把第2问的条件改为“同时,一列快车从乙地匀速驶往甲地,到达目的地只行了6小时”
①试在(1)的备用图中画出快车离甲地的距离S2(km)与行驶的时间t(h)之间的函数关系图像。
②根据图像,求出S2与t的关系式。
③
二、自觉内化
2.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设慢车行驶的时间为t(h),两车之间的距离为d(km),图中的折线表示d与t之间的函数关系.根据图象进行以下探究:
(1)请解释图中A、B、C、D 点的实际意义;即甲、乙两地的距离为 km;
(2)慢车和快车的速度和为 ;
(3)慢车的速度为 ;
(4)快车的速度为 ;
(5)求C点坐标.
(6)快车出发多长时间后,两车相距150km
三、学有所悟
通过本节课的学习,不仅感受一次函数在我们解决实际问题,特别是行程问题中更显出其直观性、优越性,使我们进一步理解了数形结合思想在数学应用中的广泛性、重要性。
四、学以致用:
小聪和小明沿同一条路同时从学校出发到常州图书馆借阅资料,学校与图书馆的路程是4千米,小明步行,小聪骑自行车。小聪15分钟到达图书馆,借阅资料花了15分钟,当小聪按原速从原路回到学校时,小明刚好到达图书馆,
问:当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
