重庆市第七高级中学校2022届高三上学期第二次月考数学试题(Word版含答案)
文档属性
| 名称 | 重庆市第七高级中学校2022届高三上学期第二次月考数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 661.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-24 22:24:58 | ||
图片预览



文档简介
重庆七中高2022级高三第二次月考
数学学科试题
一、单选题(本题共8小题,每小题5分,共40分.每小题答案只有一项是符合题目要求的.)
1. 已知角的终边经过点,则( )
A. B. C. D.
2. 已知一个扇形的圆心角为,所对的弧长为,则该扇形的面积为( )
A. B. C. D.
3. 已知某函数的图象如图所示,则下列解析式与此图象最为符合的是( )
A. B. C. D.
4. 设,则( )
A. B. C. D.
5. 某食品的保鲜时间(单位:小时)与储藏温度(单位:)满足函数关系(^为自然对数的底数,为常数).若该食品在的保鲜时间是192小时,在的保鲜时间是48小时,则该食品在的保鲜时间是( )
A.小时 B.20小时 C.24小时 D.21小时
6. 已知,则( )
A. B. C. D.
7. “当时,不等式恒成立”的一个必要不充分条件为( )
A. B. C. D.
8. 已知函数在上单调递减,且关于的方程
恰好有两个不相等的实数解,则实数的取值范围是( )
A. B. C. D.
[二、多选题(本题共4小题,每小题5分,共20分,错选不得分,少选得2分.)
9. 下列各式中,值为的是( )
A. B. C. D.
10. 已知集合,集合,集合,则
A. B. C. D.
11. 已知奇函数是定义在上的减函数,且,若,则下列结论一定成立的是( )
A. B. C. D.
12. 下列说法正确的是( )
A.已知函数,若在和处切线平行,则
B. 为了得到函数 的图象,只需将函数的图像上所有的点向左平移2个单位长度即可
C. 若,则一定成立
D. 已知函数有唯一零点,则实数
三、填空题(本题共4小题,每小题5分,共20分.把正确答案填在答题卡的横线上.)
13. .
14. 若,则 .
15. 已知,若,则的最大值为 .
16. 定义在上的函数满足,当时,,则函数在区间上的零点个数是 .
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题10分,第(I)问5分,第(II)问5分)
已知中,角、、的对边分别是、、,已知.
(I)求角的大小;
(II)若的面积为,若的周长为6,求三角形的边长.
18. (本小题12分,第(I)问6分,第(II)问6分)
已知.
(I)化简;
(II)若,且是第二象限角,求的值.
19. (本小题12分,第(I)问6分,第(II)问6分)
已知函数.
(I)求函数的解析式及定义域; (II)若恒成立,求实数的最小值.
20.(本小题12分,第(I)问4分,第(II)问8分)
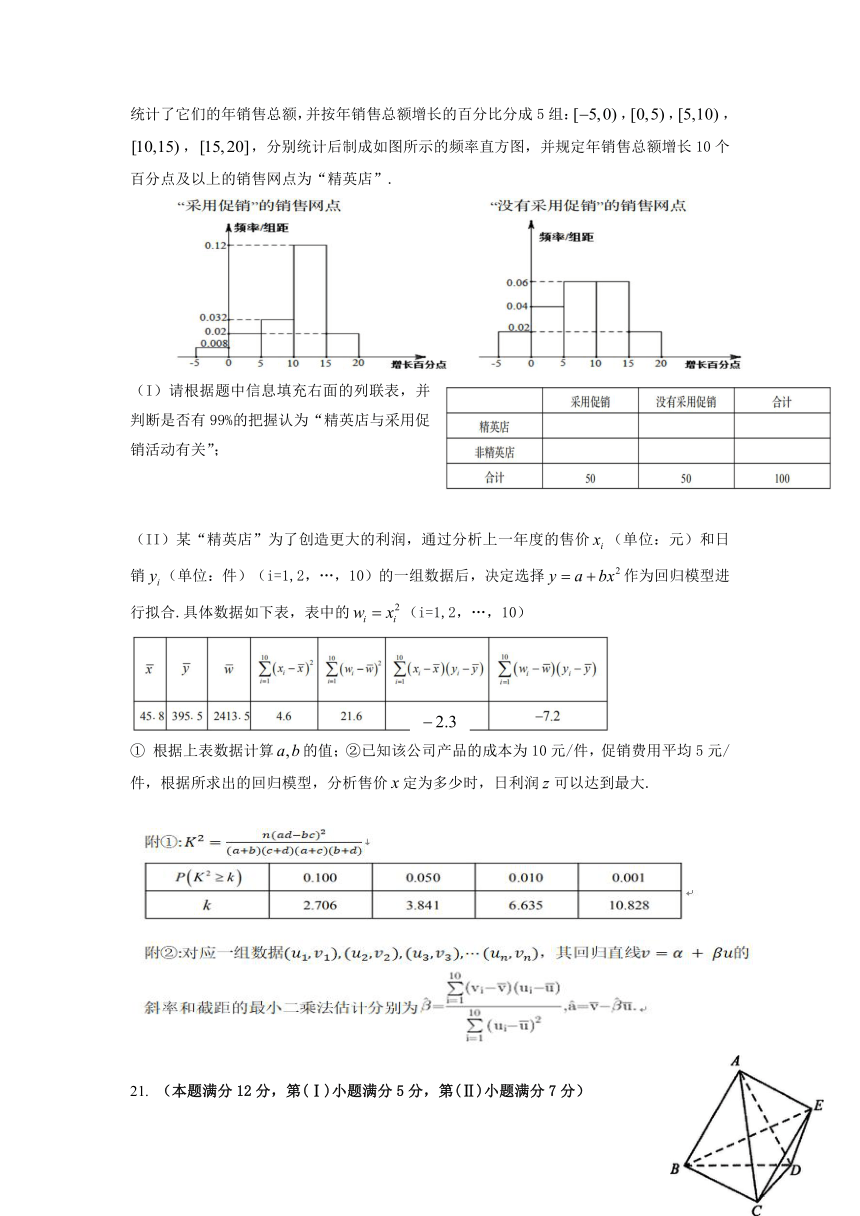
某公司设计了一套产品促销方案,并在部分地区营销网点进行试点.运作一年后,对“采用促销”和“没有采用促销”的销售网点各选取了50个,对比上一年度的销售情况,分别统计了它们的年销售总额,并按年销售总额增长的百分比分成5组:,,,,,分别统计后制成如图所示的频率直方图,并规定年销售总额增长10个百分点及以上的销售网点为“精英店”.
(I)请根据题中信息填充右面的列联表,并判断是否有99%的把握认为“精英店与采用促销活动有关”;
(II)某“精英店”为了创造更大的利润,通过分析上一年度的售价(单位:元)和日销(单位:件)(i=1,2,…,10)的一组数据后,决定选择作为回归模型进行拟合.具体数据如下表,表中的(i=1,2,…,10)
① 根据上表数据计算的值;②已知该公司产品的成本为10元/件,促销费用平均5元/件,根据所求出的回归模型,分析售价定为多少时,日利润可以达到最大.
21. (本题满分12分,第(Ⅰ)小题满分5分,第(Ⅱ)小题满分7分)
如图,在三棱锥中,是等边三角形,为空间内一点,且以为斜边的等腰直角三角形.
(I)求证:平面平面;
(II)若,试求平面与平面所成锐二面角的余弦值.
22.(本题满分12分,第(Ⅰ)小题满分5分,第(Ⅱ)小题满分7分)
已知.
(I)当时,求的最小值;
(II)若恒成立,求实数的取值范围.
高2022级高三第二次月考(数学) 参考答案
一、单选题:
1、B 2、D 3、B 4、A 5、C 6、D 7、B 8、 C
二、多选题:
9、AB 10、BCD 11、AC 12、ACD
三、填空题
13、 2 14、-3 15、4 16、 608
四、解答题
17. (I)由正弦定理得,因为,所以,
所以,整理可得,
因为,所以,所以,又,所以.
(II)由(1)知,若的面积为,所以,若的周长为6,所以,由余弦定理,得,解得.
19.解:(I)令,即
定义域为………6分
(II)令………9分
令,即,……11分
故 实数的最小值为1 ………………12分
(
20.
)
数学学科试题
一、单选题(本题共8小题,每小题5分,共40分.每小题答案只有一项是符合题目要求的.)
1. 已知角的终边经过点,则( )
A. B. C. D.
2. 已知一个扇形的圆心角为,所对的弧长为,则该扇形的面积为( )
A. B. C. D.
3. 已知某函数的图象如图所示,则下列解析式与此图象最为符合的是( )
A. B. C. D.
4. 设,则( )
A. B. C. D.
5. 某食品的保鲜时间(单位:小时)与储藏温度(单位:)满足函数关系(^为自然对数的底数,为常数).若该食品在的保鲜时间是192小时,在的保鲜时间是48小时,则该食品在的保鲜时间是( )
A.小时 B.20小时 C.24小时 D.21小时
6. 已知,则( )
A. B. C. D.
7. “当时,不等式恒成立”的一个必要不充分条件为( )
A. B. C. D.
8. 已知函数在上单调递减,且关于的方程
恰好有两个不相等的实数解,则实数的取值范围是( )
A. B. C. D.
[二、多选题(本题共4小题,每小题5分,共20分,错选不得分,少选得2分.)
9. 下列各式中,值为的是( )
A. B. C. D.
10. 已知集合,集合,集合,则
A. B. C. D.
11. 已知奇函数是定义在上的减函数,且,若,则下列结论一定成立的是( )
A. B. C. D.
12. 下列说法正确的是( )
A.已知函数,若在和处切线平行,则
B. 为了得到函数 的图象,只需将函数的图像上所有的点向左平移2个单位长度即可
C. 若,则一定成立
D. 已知函数有唯一零点,则实数
三、填空题(本题共4小题,每小题5分,共20分.把正确答案填在答题卡的横线上.)
13. .
14. 若,则 .
15. 已知,若,则的最大值为 .
16. 定义在上的函数满足,当时,,则函数在区间上的零点个数是 .
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题10分,第(I)问5分,第(II)问5分)
已知中,角、、的对边分别是、、,已知.
(I)求角的大小;
(II)若的面积为,若的周长为6,求三角形的边长.
18. (本小题12分,第(I)问6分,第(II)问6分)
已知.
(I)化简;
(II)若,且是第二象限角,求的值.
19. (本小题12分,第(I)问6分,第(II)问6分)
已知函数.
(I)求函数的解析式及定义域; (II)若恒成立,求实数的最小值.
20.(本小题12分,第(I)问4分,第(II)问8分)
某公司设计了一套产品促销方案,并在部分地区营销网点进行试点.运作一年后,对“采用促销”和“没有采用促销”的销售网点各选取了50个,对比上一年度的销售情况,分别统计了它们的年销售总额,并按年销售总额增长的百分比分成5组:,,,,,分别统计后制成如图所示的频率直方图,并规定年销售总额增长10个百分点及以上的销售网点为“精英店”.
(I)请根据题中信息填充右面的列联表,并判断是否有99%的把握认为“精英店与采用促销活动有关”;
(II)某“精英店”为了创造更大的利润,通过分析上一年度的售价(单位:元)和日销(单位:件)(i=1,2,…,10)的一组数据后,决定选择作为回归模型进行拟合.具体数据如下表,表中的(i=1,2,…,10)
① 根据上表数据计算的值;②已知该公司产品的成本为10元/件,促销费用平均5元/件,根据所求出的回归模型,分析售价定为多少时,日利润可以达到最大.
21. (本题满分12分,第(Ⅰ)小题满分5分,第(Ⅱ)小题满分7分)
如图,在三棱锥中,是等边三角形,为空间内一点,且以为斜边的等腰直角三角形.
(I)求证:平面平面;
(II)若,试求平面与平面所成锐二面角的余弦值.
22.(本题满分12分,第(Ⅰ)小题满分5分,第(Ⅱ)小题满分7分)
已知.
(I)当时,求的最小值;
(II)若恒成立,求实数的取值范围.
高2022级高三第二次月考(数学) 参考答案
一、单选题:
1、B 2、D 3、B 4、A 5、C 6、D 7、B 8、 C
二、多选题:
9、AB 10、BCD 11、AC 12、ACD
三、填空题
13、 2 14、-3 15、4 16、 608
四、解答题
17. (I)由正弦定理得,因为,所以,
所以,整理可得,
因为,所以,所以,又,所以.
(II)由(1)知,若的面积为,所以,若的周长为6,所以,由余弦定理,得,解得.
19.解:(I)令,即
定义域为………6分
(II)令………9分
令,即,……11分
故 实数的最小值为1 ………………12分
(
20.
)
同课章节目录
