2021-2022学年数学人教B版(2019)必修第二册6.2.3平面向量的坐标及其运算(第1课时)导学案
文档属性
| 名称 | 2021-2022学年数学人教B版(2019)必修第二册6.2.3平面向量的坐标及其运算(第1课时)导学案 | 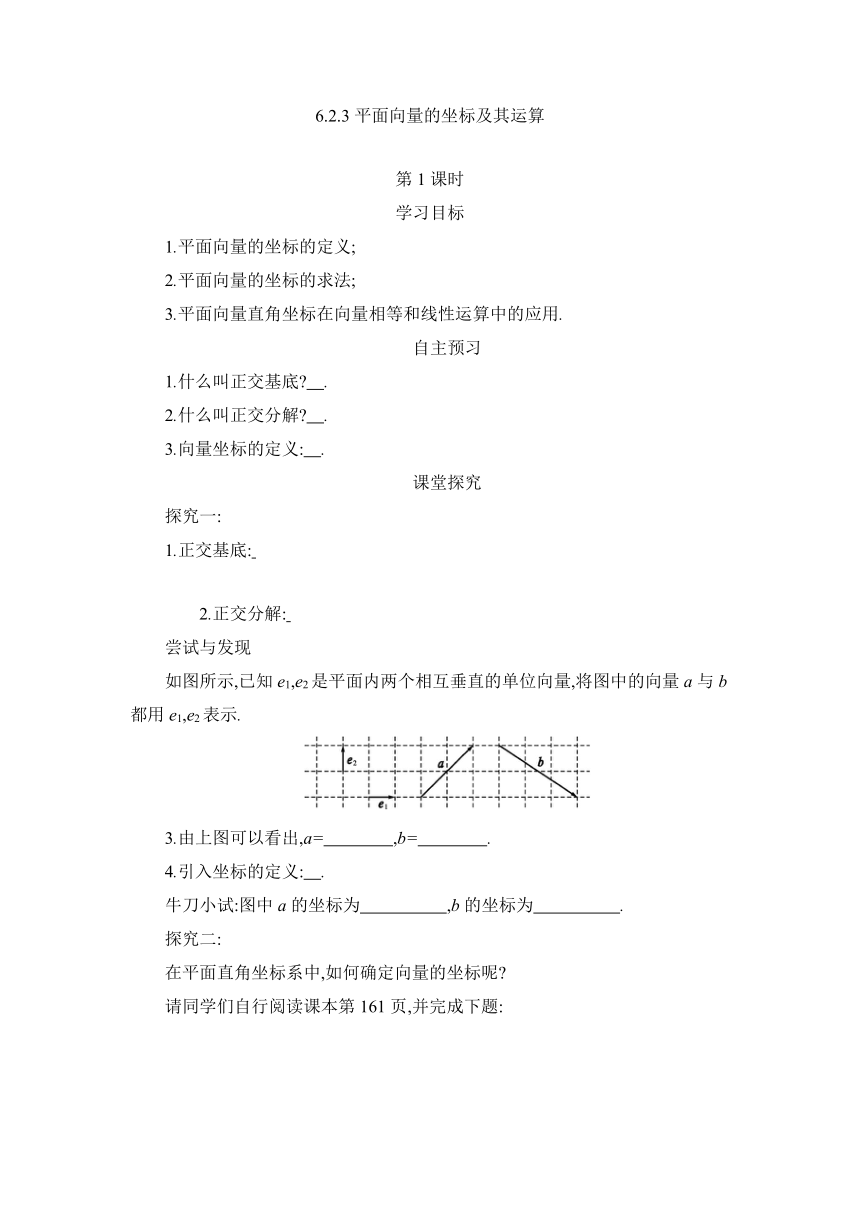 | |
| 格式 | docx | ||
| 文件大小 | 116.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-24 22:37:37 | ||
图片预览


文档简介
6.2.3平面向量的坐标及其运算
第1课时
学习目标
1.平面向量的坐标的定义;
2.平面向量的坐标的求法;
3.平面向量直角坐标在向量相等和线性运算中的应用.
自主预习
1.什么叫正交基底 .
2.什么叫正交分解 .
3.向量坐标的定义: .
课堂探究
探究一:
1.正交基底:
2.正交分解:
尝试与发现
如图所示,已知e1,e2是平面内两个相互垂直的单位向量,将图中的向量a与b都用e1,e2表示.
3.由上图可以看出,a= ,b= .
4.引入坐标的定义: .
牛刀小试:图中a的坐标为 ,b的坐标为 .
探究二:
在平面直角坐标系中,如何确定向量的坐标呢
请同学们自行阅读课本第161页,并完成下题:
图中,a= ,b= ,e1= ,e2= .
小结:1.如果平面上一点A的坐标为(x,y),那么向量对应的坐标也为 ,即= ;反之,这一结论也成立.
2.为了求出平面上向量的坐标,可以选择如下两种方法中的任何一种:
① .
② .
例1 如图所示,写出向量a,b的坐标.
探究三:
平面上的向量有了坐标之后,向量的相等以及运算与它们对应的坐标之间有什么关系呢
探究:假设平面上两个向量a,b满足a=(x1,y1),b=(x2,y2),也就是说
a=x1e1+y1e2,b= .
(1)若a=b,则x1e1+y1e2=x2e1+y2e2,坐标关系为 ;
(2)向量a+b=x1e1+y1e2+x2e1+y2e2=(x1+x2)e1+(y1+y2)e2,a+b的坐标为 ;
同理:
(3)向量a-b的坐标为 ;
(4)向量μa的坐标为 .
例2 已知a=(-2,3),b=(3,-3),求下列向量的坐标:
(1)a+b;(2)2a-5b;(3)b.
探究:由平面向量的坐标怎样表示向量的模
事实上,如果向量a不在坐标轴上时,可以构造出一个边长分别为|x|与|y|的矩形,而|a|正好等于矩形的对角线长,因此|a|=.
当a在坐标轴上时,上述结论显然也成立.
例3 已知a=(,1),b=(-2,2),求|a|,|b|.
课堂练习
1.下列说法中正确的个数是( )
①向量在平面直角坐标系xOy内的坐标是唯一的;
②若=(1,2),则的终点坐标是(1,2);
③若的终点坐标为(1,2),则=(1,2).
A.0 B.1 C.2 D.3
2.若向量=(1,2),=(3,4),则等于( )
A.(4,6) B.(-4,-6)
C.(-2,-2) D.(2,2)
3.设向量a,b满足|a|=2,b=(2,1),且a与b的方向相反,则a的坐标为 .
核心素养专练
1.若向量=(2,2),=(-2,3)分别表示两个力F1,F2,则|F1+F2|为( )
A.(0,5) B.(4,-1)
C.2 D.5
2.已知=a,且A,B,又λ=,则λa等于( )
A. B.
C. D.
参考答案
自主预习
略
课堂探究
探究一:
1.如果平面向量的基底{e1,e2}中,e1⊥e2,就称这组基底为正交基底.
2.在正交基底下向量的分解称为向量的正交分解
3.2e1+2e2 3e1-2e2
4.一般地,给定平面内两个互相垂直的单位向量e1,e2,对于平面内的向量a,如果a=xe1+ye2,则称(x,y)为向量当a的坐标,记作a=(x,y)
牛刀小试:(2,2) (3,-2)
探究二:
(4,2) (-3,-1) (1,0) (0,1)
小结:1.(x,y) (x,y)
2.①将向量用正交单位向量e1,e2表示出来,读出向量的坐标(探究一)
②将向量的始点平移到原点,读出终点的坐标,即向量的坐标(探究二)
例1 解:因为a的始点在原点,所以由a的终点坐标知a=(5,-1).
又因为b=4e1+e2,所以b=(-4,1).
探究三:
探究:x2e1+y2e2
(1)x1=x2且y1=y2
(2)(x1+x2,y1+y2)
(3)(x1-x2,y1-y2)
(4)(μx1,μy1)
例2
解:(1)a+b=(-2,3)+(3,-3)=(-2+3,3-3)=(1,0).
(2)2a-5b=2(-2,3)-5(3,-3)=(-4,6)-(15,-15)=(-19,21).
(3)b=(3,-3)=(1,-1).
例3 解:由已知可得
|a|==2,|b|==4.
课堂练习
1.B 解析:因为e1,e2为正交基底,所以①正确;向量的坐标与表示该向量的有向线段的始点、终点的具体位置无关,只与其相对位置有关,故②③不正确.
2.A 解析:=+=(1,2)+(3,4)=(4,6).
3.解析:因为b=(2,1),且a与b的方向相反,
所以设a=(2λ,λ)(λ<0).
因为|a|=2,所以4λ2+λ2=20,λ2=4,λ=-2,
所以a=(-4,-2).
答案:(-4,-2)
核心素养专练
1.D
2.A
第1课时
学习目标
1.平面向量的坐标的定义;
2.平面向量的坐标的求法;
3.平面向量直角坐标在向量相等和线性运算中的应用.
自主预习
1.什么叫正交基底 .
2.什么叫正交分解 .
3.向量坐标的定义: .
课堂探究
探究一:
1.正交基底:
2.正交分解:
尝试与发现
如图所示,已知e1,e2是平面内两个相互垂直的单位向量,将图中的向量a与b都用e1,e2表示.
3.由上图可以看出,a= ,b= .
4.引入坐标的定义: .
牛刀小试:图中a的坐标为 ,b的坐标为 .
探究二:
在平面直角坐标系中,如何确定向量的坐标呢
请同学们自行阅读课本第161页,并完成下题:
图中,a= ,b= ,e1= ,e2= .
小结:1.如果平面上一点A的坐标为(x,y),那么向量对应的坐标也为 ,即= ;反之,这一结论也成立.
2.为了求出平面上向量的坐标,可以选择如下两种方法中的任何一种:
① .
② .
例1 如图所示,写出向量a,b的坐标.
探究三:
平面上的向量有了坐标之后,向量的相等以及运算与它们对应的坐标之间有什么关系呢
探究:假设平面上两个向量a,b满足a=(x1,y1),b=(x2,y2),也就是说
a=x1e1+y1e2,b= .
(1)若a=b,则x1e1+y1e2=x2e1+y2e2,坐标关系为 ;
(2)向量a+b=x1e1+y1e2+x2e1+y2e2=(x1+x2)e1+(y1+y2)e2,a+b的坐标为 ;
同理:
(3)向量a-b的坐标为 ;
(4)向量μa的坐标为 .
例2 已知a=(-2,3),b=(3,-3),求下列向量的坐标:
(1)a+b;(2)2a-5b;(3)b.
探究:由平面向量的坐标怎样表示向量的模
事实上,如果向量a不在坐标轴上时,可以构造出一个边长分别为|x|与|y|的矩形,而|a|正好等于矩形的对角线长,因此|a|=.
当a在坐标轴上时,上述结论显然也成立.
例3 已知a=(,1),b=(-2,2),求|a|,|b|.
课堂练习
1.下列说法中正确的个数是( )
①向量在平面直角坐标系xOy内的坐标是唯一的;
②若=(1,2),则的终点坐标是(1,2);
③若的终点坐标为(1,2),则=(1,2).
A.0 B.1 C.2 D.3
2.若向量=(1,2),=(3,4),则等于( )
A.(4,6) B.(-4,-6)
C.(-2,-2) D.(2,2)
3.设向量a,b满足|a|=2,b=(2,1),且a与b的方向相反,则a的坐标为 .
核心素养专练
1.若向量=(2,2),=(-2,3)分别表示两个力F1,F2,则|F1+F2|为( )
A.(0,5) B.(4,-1)
C.2 D.5
2.已知=a,且A,B,又λ=,则λa等于( )
A. B.
C. D.
参考答案
自主预习
略
课堂探究
探究一:
1.如果平面向量的基底{e1,e2}中,e1⊥e2,就称这组基底为正交基底.
2.在正交基底下向量的分解称为向量的正交分解
3.2e1+2e2 3e1-2e2
4.一般地,给定平面内两个互相垂直的单位向量e1,e2,对于平面内的向量a,如果a=xe1+ye2,则称(x,y)为向量当a的坐标,记作a=(x,y)
牛刀小试:(2,2) (3,-2)
探究二:
(4,2) (-3,-1) (1,0) (0,1)
小结:1.(x,y) (x,y)
2.①将向量用正交单位向量e1,e2表示出来,读出向量的坐标(探究一)
②将向量的始点平移到原点,读出终点的坐标,即向量的坐标(探究二)
例1 解:因为a的始点在原点,所以由a的终点坐标知a=(5,-1).
又因为b=4e1+e2,所以b=(-4,1).
探究三:
探究:x2e1+y2e2
(1)x1=x2且y1=y2
(2)(x1+x2,y1+y2)
(3)(x1-x2,y1-y2)
(4)(μx1,μy1)
例2
解:(1)a+b=(-2,3)+(3,-3)=(-2+3,3-3)=(1,0).
(2)2a-5b=2(-2,3)-5(3,-3)=(-4,6)-(15,-15)=(-19,21).
(3)b=(3,-3)=(1,-1).
例3 解:由已知可得
|a|==2,|b|==4.
课堂练习
1.B 解析:因为e1,e2为正交基底,所以①正确;向量的坐标与表示该向量的有向线段的始点、终点的具体位置无关,只与其相对位置有关,故②③不正确.
2.A 解析:=+=(1,2)+(3,4)=(4,6).
3.解析:因为b=(2,1),且a与b的方向相反,
所以设a=(2λ,λ)(λ<0).
因为|a|=2,所以4λ2+λ2=20,λ2=4,λ=-2,
所以a=(-4,-2).
答案:(-4,-2)
核心素养专练
1.D
2.A
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
