3.1 建立一元一次方程模型 课件(共28张PPT)
文档属性
| 名称 | 3.1 建立一元一次方程模型 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 45.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-25 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
3.1 建立一元一次方程模型
湘教版 七年级上
教学目标
1.理解一元一次方程的概念,认识一元一次方程模型;
2.理解方程的解概念,能对方程的解进行判断;
3.能建立简单问题的方程模型;
4.体会方程的应用价值,感知数学与现实生活的联系.
1. 张大叔从家里骑电动车去上班,平均速度为xkm/h,每
天要骑0.5h,张大叔家到上班单位的路程是 km;
2. 一个长方体食品盒的长、宽、高分别是4、3、y,则这
个食品盒的表面积是 .
新知导入
0.5x
24+8y+6y
做一做:
1. 如果已知张大叔家到上班单位的路程是14km,你还能
写出一个含x的式子吗?
2. 如果已知这个食品盒的表面积是52,你还能写出一个
含y的式子吗?
新知导入
0.5x=14
24+8y+6y=52
问题:
这样的式子是怎样得到的?它们有什么共同的特点?我们把这样的式子叫作什么?
新知讲解
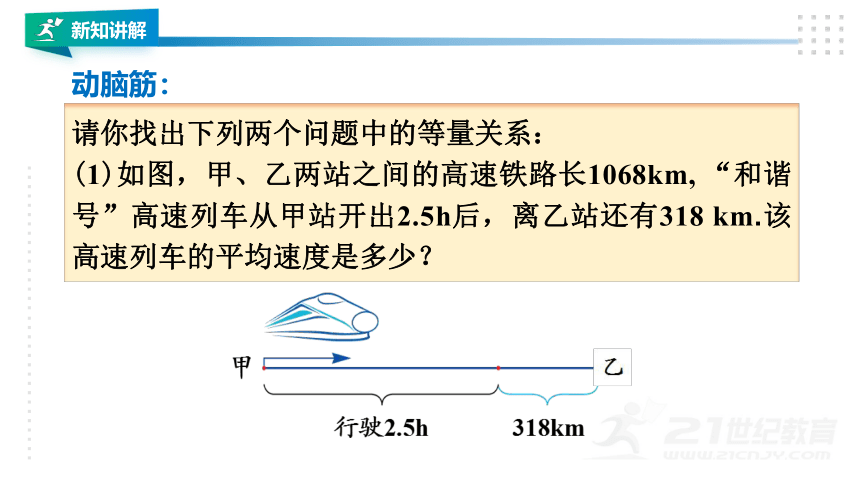
请你找出下列两个问题中的等量关系:
(1)如图,甲、乙两站之间的高速铁路长1068km, “和谐号”高速列车从甲站开出2.5h后,离乙站还有318 km.该高速列车的平均速度是多少?
动脑筋:
新知讲解
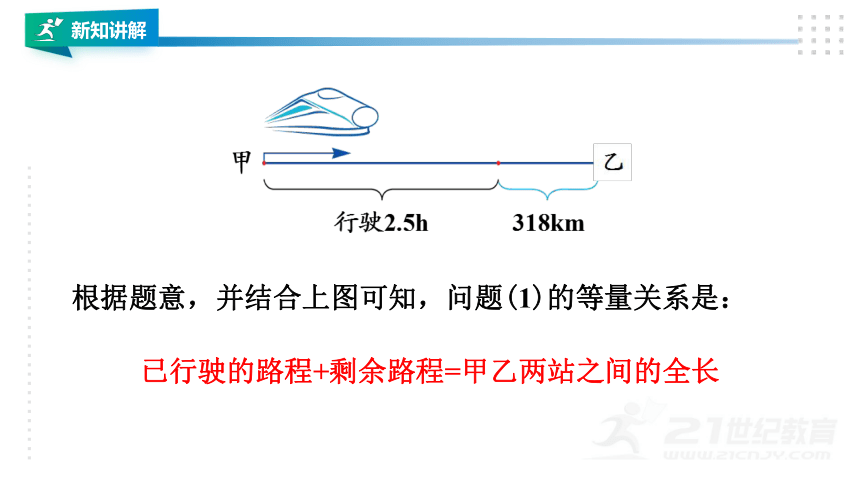
根据题意,并结合上图可知,问题(1)的等量关系是:
已行驶的路程+剩余路程=甲乙两站之间的全长
新知讲解
在上述等量关系中,剩余路程是318km,甲、乙两站之间的全长为1 068km。如果设高速列车的平均速度为xkm/h,则已行驶的路程为2.5xkm。
于是,用含x的式子表示上述等量关系就是:
已行驶的路程+剩余路程=甲乙两站之间的全长
2.5x+318=1 068
①
如何用式子表示问题(1)中的等量关系呢?
新知讲解
(2)右图是一个长方体形的包装盒,长为1.2m,高为1m,表面积为6.8m2. 这个包装盒的底面宽是多少?
根据划线部分“表面积为6.8m2”,结合长方体的表面积的计算方法,得到的等量关系是:
长×宽×2+长×高×2+宽×高×2=表面积6.8m2
新知讲解
ym
设这个包装盒的底面宽是ym,把上述等量关系中的长用1.2表示,宽用y表示,高用1表示,运算符号不变,则上述等量关系可表示为:
长×宽×2+长×高×2+宽×高×2=表面积6.8m2
如何用式子表示问题(2)中的等量关系?
1.2×y×2+y×1×2+1.2×1×2=6.8
即 2.4y+2y+2.4=6.8
②
新知讲解
在等式2.5x+318 =1068中,2.5,318,1068 叫做已知数,字母x表示的数,在解决这个问题之前还不知道,把它叫做未知数.我们把含有未知数的等式叫做方程.
例如,2.5x+318=1068,2.4y+2y+2.4=6.8,x-2y=6,
中,x, y, t 都是未知数,这些等式都
是方程.
概念:
新知讲解
像上面这样,把所要求的量用字母x(或y,…)表示,根据问题的等量关系列出方程,这一过程叫作建立方程.
概念:
新知讲解
说一说:
观察方程①、②中,说说每个方程含有几个未知数?每个未知数的次数是多少?
2.5x+318=1 068 ①
2.4y+2y+2.4=6.8 ②
方程①中,含有1个未知数x,未知数x的次数是1.
方程①中,含有1个未知数y,未知数y的次数也是1.
新知讲解
像方程2.5x+318 =1068,2.4y+2y+2.4=6.8这样,只含有一个未知数,并且未知数的次数是1,我们把这样的方程叫做一元一次方程.
概念:
新知讲解
在方程x+5=9中,当x=4时,方程两边的值相等,我们就说x=4是方程x+5=9的解.
能使方程左、右两边相等的未知数的值叫做方程的解.
例题讲解
例 检验下列x的值是否是方程2.5x+318=1068的解.
(1) x = 300 (2) x = 330.
解(1)把x =300代入原方程得,
左边=2.5×300+318=1068,
左边=右边,
所以x=300是方程2.5x+318=1068的解.
例题讲解
例 检验下列x的值是否是方程2.5x+318=1068的解.
(1) x = 300 (2) x = 330.
(2)把x=330代入原方程得,
左边=2.5×330+318=1143,
左边≠右边,
所以x=330不是方程2.5x+318=1068的解.
巩固练习
1. 下列各式是一元一次方程的是 ( )
A. 4x+y=6 B. 5x+3
C. x+5=1-x D. 1
提示:一元一次方程必须满足下列条件:
(1)是含有未知数的等式; (2)只含有一个未知数;
(3)未知数的次数是1; (4)化简后系数不为0;
(5)是整式方程,即分母中不含字母。
C
巩固练习
2. 已知关于x的一元一次方程,则a
的是 ( )
A. 2 B. -2 C. ±1 D. ±2
B
巩固练习
3. 一元一次方程的解是 ( )
A. =3 B. =-3
C. =4 D. -6
B
提示:检验一个未知数的值是否为方程的解,可以把这个值分别代入方程的两边,若左、右两边的值相等,则为方程的解;否则不是方程的解。
课堂总结
含有未知数的等式叫做方程。
只含有一个未知数,并且未知数的次数是1的方程叫做一元一次方程。
1. 什么叫做方程?什么叫做一元一次方程?
2. 什么叫做方程的解?
能使方程左、右两边相等的未知数的值叫做方程的解.
课堂总结
先分析问题的等量关系,再把所要求的量用字母x(或y,…)表示。
3. 如何建立方程?
4. 如何检验方程的解?
先把未知数的值代入方程左、右两边计算,再根据计算结果是否左、右两边相等判断是否是方程的解.
作业布置
第84、85页课后练习:
1. 下面哪些方程是一元一次方程?
是
不是
(1)3x+ 4 = 5x -1;
(2)2x2 - x - 1 = 0 ;
(3)x-2y=4;
(4)3(2x-7)=4(x- 5).
不是
是
作业布置
2. 检验下列x的值是否是方程2x-6=7x+4的解.
(1)x =2; (2)x = -2.
解(1)把 x = 2 代入方程左右两边,
左边=2×2-6=-2
右边=7×2+4=18
左边≠右边
所以 x=2 不是方程2x-6=7x+4的解.
作业布置
(2)把x=-2代入方程2x-6=7x+4左右两边,
左边=2×(-2)-6=-10
右边=7×(-2)+4=-10
左边=右边
所以x=-2是方程2x-6=7x+4的解.
作业布置
3. 建立下列各问题中的方程模型:
(1)2011年6月底,我国网民达4.85亿,比2008 年6月底
的1.9倍还多430万人,则2008年6月底网民数是多少?
解 设2008年6月底网民数为x 万人. 根据题意,
得 1.9x +0.043 = 4.85
作业布置
(2)排球场的长比宽多9m,周长是54m,排球场的宽为多少?
解 设排球场的宽为x m,根据
题意,得
2(x+x+9)= 54
https://www.21cnjy.com/help/help_extract.php
3.1 建立一元一次方程模型
湘教版 七年级上
教学目标
1.理解一元一次方程的概念,认识一元一次方程模型;
2.理解方程的解概念,能对方程的解进行判断;
3.能建立简单问题的方程模型;
4.体会方程的应用价值,感知数学与现实生活的联系.
1. 张大叔从家里骑电动车去上班,平均速度为xkm/h,每
天要骑0.5h,张大叔家到上班单位的路程是 km;
2. 一个长方体食品盒的长、宽、高分别是4、3、y,则这
个食品盒的表面积是 .
新知导入
0.5x
24+8y+6y
做一做:
1. 如果已知张大叔家到上班单位的路程是14km,你还能
写出一个含x的式子吗?
2. 如果已知这个食品盒的表面积是52,你还能写出一个
含y的式子吗?
新知导入
0.5x=14
24+8y+6y=52
问题:
这样的式子是怎样得到的?它们有什么共同的特点?我们把这样的式子叫作什么?
新知讲解
请你找出下列两个问题中的等量关系:
(1)如图,甲、乙两站之间的高速铁路长1068km, “和谐号”高速列车从甲站开出2.5h后,离乙站还有318 km.该高速列车的平均速度是多少?
动脑筋:
新知讲解
根据题意,并结合上图可知,问题(1)的等量关系是:
已行驶的路程+剩余路程=甲乙两站之间的全长
新知讲解
在上述等量关系中,剩余路程是318km,甲、乙两站之间的全长为1 068km。如果设高速列车的平均速度为xkm/h,则已行驶的路程为2.5xkm。
于是,用含x的式子表示上述等量关系就是:
已行驶的路程+剩余路程=甲乙两站之间的全长
2.5x+318=1 068
①
如何用式子表示问题(1)中的等量关系呢?
新知讲解
(2)右图是一个长方体形的包装盒,长为1.2m,高为1m,表面积为6.8m2. 这个包装盒的底面宽是多少?
根据划线部分“表面积为6.8m2”,结合长方体的表面积的计算方法,得到的等量关系是:
长×宽×2+长×高×2+宽×高×2=表面积6.8m2
新知讲解
ym
设这个包装盒的底面宽是ym,把上述等量关系中的长用1.2表示,宽用y表示,高用1表示,运算符号不变,则上述等量关系可表示为:
长×宽×2+长×高×2+宽×高×2=表面积6.8m2
如何用式子表示问题(2)中的等量关系?
1.2×y×2+y×1×2+1.2×1×2=6.8
即 2.4y+2y+2.4=6.8
②
新知讲解
在等式2.5x+318 =1068中,2.5,318,1068 叫做已知数,字母x表示的数,在解决这个问题之前还不知道,把它叫做未知数.我们把含有未知数的等式叫做方程.
例如,2.5x+318=1068,2.4y+2y+2.4=6.8,x-2y=6,
中,x, y, t 都是未知数,这些等式都
是方程.
概念:
新知讲解
像上面这样,把所要求的量用字母x(或y,…)表示,根据问题的等量关系列出方程,这一过程叫作建立方程.
概念:
新知讲解
说一说:
观察方程①、②中,说说每个方程含有几个未知数?每个未知数的次数是多少?
2.5x+318=1 068 ①
2.4y+2y+2.4=6.8 ②
方程①中,含有1个未知数x,未知数x的次数是1.
方程①中,含有1个未知数y,未知数y的次数也是1.
新知讲解
像方程2.5x+318 =1068,2.4y+2y+2.4=6.8这样,只含有一个未知数,并且未知数的次数是1,我们把这样的方程叫做一元一次方程.
概念:
新知讲解
在方程x+5=9中,当x=4时,方程两边的值相等,我们就说x=4是方程x+5=9的解.
能使方程左、右两边相等的未知数的值叫做方程的解.
例题讲解
例 检验下列x的值是否是方程2.5x+318=1068的解.
(1) x = 300 (2) x = 330.
解(1)把x =300代入原方程得,
左边=2.5×300+318=1068,
左边=右边,
所以x=300是方程2.5x+318=1068的解.
例题讲解
例 检验下列x的值是否是方程2.5x+318=1068的解.
(1) x = 300 (2) x = 330.
(2)把x=330代入原方程得,
左边=2.5×330+318=1143,
左边≠右边,
所以x=330不是方程2.5x+318=1068的解.
巩固练习
1. 下列各式是一元一次方程的是 ( )
A. 4x+y=6 B. 5x+3
C. x+5=1-x D. 1
提示:一元一次方程必须满足下列条件:
(1)是含有未知数的等式; (2)只含有一个未知数;
(3)未知数的次数是1; (4)化简后系数不为0;
(5)是整式方程,即分母中不含字母。
C
巩固练习
2. 已知关于x的一元一次方程,则a
的是 ( )
A. 2 B. -2 C. ±1 D. ±2
B
巩固练习
3. 一元一次方程的解是 ( )
A. =3 B. =-3
C. =4 D. -6
B
提示:检验一个未知数的值是否为方程的解,可以把这个值分别代入方程的两边,若左、右两边的值相等,则为方程的解;否则不是方程的解。
课堂总结
含有未知数的等式叫做方程。
只含有一个未知数,并且未知数的次数是1的方程叫做一元一次方程。
1. 什么叫做方程?什么叫做一元一次方程?
2. 什么叫做方程的解?
能使方程左、右两边相等的未知数的值叫做方程的解.
课堂总结
先分析问题的等量关系,再把所要求的量用字母x(或y,…)表示。
3. 如何建立方程?
4. 如何检验方程的解?
先把未知数的值代入方程左、右两边计算,再根据计算结果是否左、右两边相等判断是否是方程的解.
作业布置
第84、85页课后练习:
1. 下面哪些方程是一元一次方程?
是
不是
(1)3x+ 4 = 5x -1;
(2)2x2 - x - 1 = 0 ;
(3)x-2y=4;
(4)3(2x-7)=4(x- 5).
不是
是
作业布置
2. 检验下列x的值是否是方程2x-6=7x+4的解.
(1)x =2; (2)x = -2.
解(1)把 x = 2 代入方程左右两边,
左边=2×2-6=-2
右边=7×2+4=18
左边≠右边
所以 x=2 不是方程2x-6=7x+4的解.
作业布置
(2)把x=-2代入方程2x-6=7x+4左右两边,
左边=2×(-2)-6=-10
右边=7×(-2)+4=-10
左边=右边
所以x=-2是方程2x-6=7x+4的解.
作业布置
3. 建立下列各问题中的方程模型:
(1)2011年6月底,我国网民达4.85亿,比2008 年6月底
的1.9倍还多430万人,则2008年6月底网民数是多少?
解 设2008年6月底网民数为x 万人. 根据题意,
得 1.9x +0.043 = 4.85
作业布置
(2)排球场的长比宽多9m,周长是54m,排球场的宽为多少?
解 设排球场的宽为x m,根据
题意,得
2(x+x+9)= 54
https://www.21cnjy.com/help/help_extract.php
同课章节目录
