2012高一物理课件:第一章 章末整合 (粤教版必修2)
文档属性
| 名称 | 2012高一物理课件:第一章 章末整合 (粤教版必修2) |  | |
| 格式 | zip | ||
| 文件大小 | 378.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 广东版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-08-27 21:12:25 | ||
图片预览





文档简介
(共16张PPT)
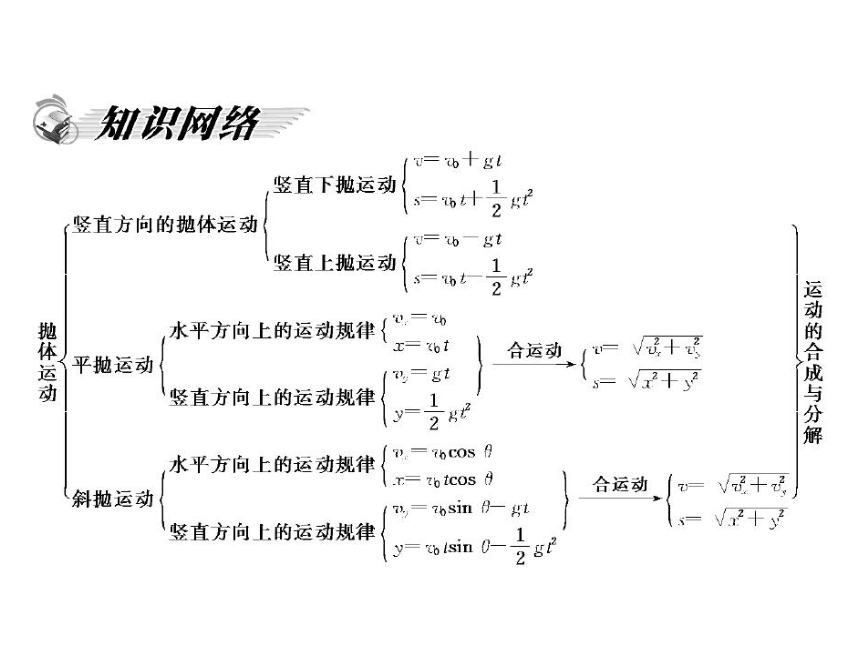
专题一 运动的合成与分解
运动的合成与分解是处理曲线运动的方法之一,关键是分
清合运动与分运动.运动的分解可以任意分解,但通常情况下
是按相互正交的两个方向分解,以构成平行四边形或三角形求
解.
在对运动进行合成与分解时,要抓住合运动与分运动独立
性、等效性和等时性的特点分析处理问题.
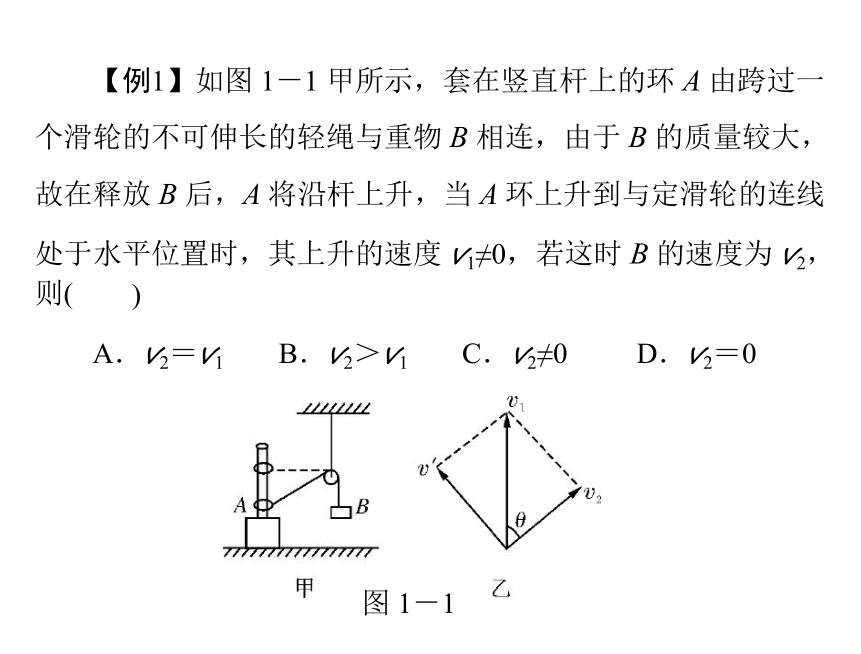
【例1】如图 1-1 甲所示,套在竖直杆上的环 A 由跨过一
个滑轮的不可伸长的轻绳与重物 B 相连,由于 B 的质量较大,
故在释放 B 后,A 将沿杆上升,当 A 环上升到与定滑轮的连线
处于水平位置时,其上升的速度 v1≠0,若这时 B 的速度为 v2,
则(
)
A.v2=v1
B.v2>v1
C.v2≠0
D.v2=0
图 1-1
解析:如图1-1 乙所示,环上升过程,其速度v1 可分解
为沿绳方向的速度v2 和垂直于绳子方向的速度 v′.由直角三角
形得v2=v1cos θ,当A 环上升到与定滑轮的连线处于水平位置
时,θ=90°,即v2=v1cos 90°=0,故 D 答案正确.
答案:D
运动的合成与分解的一般思路:
(1)确定合运动:明确研究对象,分析与研究相关联的运动,
在这些运动中以地面为参照系的运动为合运动.
(2)运动的分解:按运动的实际效果及正交分解法进行分
解.
专题二 抛体运动的综合处理
抛体运动均是初速度不为零、仅受重力作用的匀变速运动.
判断其做直线运动还是做曲线运动的条件是:分析其初速度是
否与重力共线.但不管是直线运动还是曲线运动,处理方法都
是运用运动的分解来处理.对于分解运动的哪个物理量视具体
情况而定,题目给出了哪个物理量的大小和方向就分解哪个.
【例2】如图 1-2 所示,一高度为 h=0.2 m 的水平面在 A
点处与一倾角为θ=30°的斜面连接,一小球以v0=5 m/s 的速度
在平面上向右运动,求小球从 A 点运动到地面所需的时间.(平
面与斜面均光滑,g 取 10 m/s2)
图 1-2
解:假设无斜面,则落地点与 A 点的水平距离
则小球在 A 点离开平面做平抛运动,不会沿斜面下滑,所
以小球从 A 点运动到地面所需的时间为t=
=0.2 s.
1.(双选,2011 年广东卷)如图 1-3 所示,在网球的网前
截击练习中,若练习者在球网正上方距地面 H 处,将球以速度
v 沿垂直球网的方向击出,球刚好落在底线上.已知底线到网
的距离为 L,重力加速度取 g,将球的运动视作平抛运动,下列
表述正确的是(
)
图 1-3
A.球的速度 v 等于 L
B.球从击出至落地所用时间为
C.球从击球点至落地点的位移等于 L
D.球从击球点至落地点的位移与球的质量有关
解析:球做平抛运动,平抛运动是水平方向上的匀速直线
运动和竖直方向上的自由落体运动的合运动,球的初速度 v=
L
.球从击出到落地的时间 t=
.球从击球点至落地点
的位移等于 .
答案:AB
2.(2011 年上海卷)如图 1-4 所示,人沿平直的河岸以速
度 v 行走,且通过不可伸长的绳拖船,船沿绳的方向行进,此
过程中绳始终与水面平行.当绳与河岸的夹角为α时,船的速率
为(
)
C
图 1-4
A.vsin α
B.
v
sin α
C.vcos α
D.
v
cos α
解析:依题意船沿着绳子的方向前进,即船的速度就是沿
着绳子的,根据绳子连接的两端物体的速度在绳子上的投影速
度相同,即人的速度v在绳子方向的分量等于船速,故v船=vcos
α,选项C 对.
3.(2011 年江苏卷)如图 1-5 所示,甲、乙两同学从河中
O 点出发,分别沿直线游到 A 点和 B 点后,立即沿原路线返回
到 O 点,OA、OB 分别与水流方向平行和垂直,且 OA=OB.
若水流速度不变,两人在静水中游速相等,则他们所用时间t甲、
)
t乙的大小关系为(
A.t甲B.t甲=t乙
C.t甲>t乙
D.无法确定
图 1-5
答案:C
图 6
4.(2010 年全国卷Ⅰ)一水平抛出的小球落到一倾角为θ的
斜面上时,其速度方向与斜面垂直,运动轨迹如图 1-6 中虚线
所示.小球在竖直方向下落的距离与在水平方向通过的距离之
比为(
)
A.tan θ
B.2tan θ
C.
1
tan θ
D.
1
2tan θ
图 1-6
解析:如图 7,平抛的末速度与竖直方向的夹角等于斜面
答案:D
图 7
5.(2011 年海南卷)如图 1-7,水平地面上有一个坑,其竖
直截面为半圆.ab 为沿水平方向的直径.若在 a 点以初速度 v0
沿 ab 方向抛出一小球,小球会击中坑壁上的 c 点.已知 c 点与
水平地面的距离为圆半径的一半,求圆的半径.
图 1-7
专题一 运动的合成与分解
运动的合成与分解是处理曲线运动的方法之一,关键是分
清合运动与分运动.运动的分解可以任意分解,但通常情况下
是按相互正交的两个方向分解,以构成平行四边形或三角形求
解.
在对运动进行合成与分解时,要抓住合运动与分运动独立
性、等效性和等时性的特点分析处理问题.
【例1】如图 1-1 甲所示,套在竖直杆上的环 A 由跨过一
个滑轮的不可伸长的轻绳与重物 B 相连,由于 B 的质量较大,
故在释放 B 后,A 将沿杆上升,当 A 环上升到与定滑轮的连线
处于水平位置时,其上升的速度 v1≠0,若这时 B 的速度为 v2,
则(
)
A.v2=v1
B.v2>v1
C.v2≠0
D.v2=0
图 1-1
解析:如图1-1 乙所示,环上升过程,其速度v1 可分解
为沿绳方向的速度v2 和垂直于绳子方向的速度 v′.由直角三角
形得v2=v1cos θ,当A 环上升到与定滑轮的连线处于水平位置
时,θ=90°,即v2=v1cos 90°=0,故 D 答案正确.
答案:D
运动的合成与分解的一般思路:
(1)确定合运动:明确研究对象,分析与研究相关联的运动,
在这些运动中以地面为参照系的运动为合运动.
(2)运动的分解:按运动的实际效果及正交分解法进行分
解.
专题二 抛体运动的综合处理
抛体运动均是初速度不为零、仅受重力作用的匀变速运动.
判断其做直线运动还是做曲线运动的条件是:分析其初速度是
否与重力共线.但不管是直线运动还是曲线运动,处理方法都
是运用运动的分解来处理.对于分解运动的哪个物理量视具体
情况而定,题目给出了哪个物理量的大小和方向就分解哪个.
【例2】如图 1-2 所示,一高度为 h=0.2 m 的水平面在 A
点处与一倾角为θ=30°的斜面连接,一小球以v0=5 m/s 的速度
在平面上向右运动,求小球从 A 点运动到地面所需的时间.(平
面与斜面均光滑,g 取 10 m/s2)
图 1-2
解:假设无斜面,则落地点与 A 点的水平距离
则小球在 A 点离开平面做平抛运动,不会沿斜面下滑,所
以小球从 A 点运动到地面所需的时间为t=
=0.2 s.
1.(双选,2011 年广东卷)如图 1-3 所示,在网球的网前
截击练习中,若练习者在球网正上方距地面 H 处,将球以速度
v 沿垂直球网的方向击出,球刚好落在底线上.已知底线到网
的距离为 L,重力加速度取 g,将球的运动视作平抛运动,下列
表述正确的是(
)
图 1-3
A.球的速度 v 等于 L
B.球从击出至落地所用时间为
C.球从击球点至落地点的位移等于 L
D.球从击球点至落地点的位移与球的质量有关
解析:球做平抛运动,平抛运动是水平方向上的匀速直线
运动和竖直方向上的自由落体运动的合运动,球的初速度 v=
L
.球从击出到落地的时间 t=
.球从击球点至落地点
的位移等于 .
答案:AB
2.(2011 年上海卷)如图 1-4 所示,人沿平直的河岸以速
度 v 行走,且通过不可伸长的绳拖船,船沿绳的方向行进,此
过程中绳始终与水面平行.当绳与河岸的夹角为α时,船的速率
为(
)
C
图 1-4
A.vsin α
B.
v
sin α
C.vcos α
D.
v
cos α
解析:依题意船沿着绳子的方向前进,即船的速度就是沿
着绳子的,根据绳子连接的两端物体的速度在绳子上的投影速
度相同,即人的速度v在绳子方向的分量等于船速,故v船=vcos
α,选项C 对.
3.(2011 年江苏卷)如图 1-5 所示,甲、乙两同学从河中
O 点出发,分别沿直线游到 A 点和 B 点后,立即沿原路线返回
到 O 点,OA、OB 分别与水流方向平行和垂直,且 OA=OB.
若水流速度不变,两人在静水中游速相等,则他们所用时间t甲、
)
t乙的大小关系为(
A.t甲
C.t甲>t乙
D.无法确定
图 1-5
答案:C
图 6
4.(2010 年全国卷Ⅰ)一水平抛出的小球落到一倾角为θ的
斜面上时,其速度方向与斜面垂直,运动轨迹如图 1-6 中虚线
所示.小球在竖直方向下落的距离与在水平方向通过的距离之
比为(
)
A.tan θ
B.2tan θ
C.
1
tan θ
D.
1
2tan θ
图 1-6
解析:如图 7,平抛的末速度与竖直方向的夹角等于斜面
答案:D
图 7
5.(2011 年海南卷)如图 1-7,水平地面上有一个坑,其竖
直截面为半圆.ab 为沿水平方向的直径.若在 a 点以初速度 v0
沿 ab 方向抛出一小球,小球会击中坑壁上的 c 点.已知 c 点与
水平地面的距离为圆半径的一半,求圆的半径.
图 1-7
同课章节目录
- 第一章 抛体运动
- 第01节 什么是抛体运动
- 第02节 运动的合成与分解
- 第03节 竖直方向的抛体运动
- 第04节 平抛运动
- 第05节 斜抛运动
- 第二章 圆周运动
- 第01节 匀速圆周运动
- 第02节 向心力
- 第03节 离心现象及其应用
- 第三章 万有引力定律及其应用
- 第01节 万有引力定律
- 第02节 万有引力定律的应用
- 第03节 飞向太空
- 第四章 机械能和能源
- 第01节 功
- 第02节 动能 势能
- 第03节 探究外力做功与物体动能变化的关系
- 第04节 机械能守恒定律
- 第05节 验证机械能守恒定律
- 第06节 能量 能量转化与守恒定律
- 第07节 功率
- 第08节 能源的开发与利用
- 第五章 经典力学与物理学的革命
- 第01节 经典力学的成就与局限性
- 第02节 经典时空观与相对论时空观
- 第03节 量子化现象
- 第04节 物理学——人类文明进步的阶梯
