人教版八上高分笔记之导与练13.3.1等腰三角形的性质(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练13.3.1等腰三角形的性质(原卷+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-24 17:41:20 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
13.3等腰三角形
第1课时 等腰三角形的性质
知识要点:
等腰三角形的两个底角_________
2.等腰三角形的 __________ 、_________、_________ 相互重合.
3.等腰三角形是_________ 图形,其对称轴是__________________.
易错点睛:
等腰三角形的两边长分别为6cm,13cm,其周长为_________
2.已知等腰三角形的一个角为另一个角的2倍,则这角为 __________________
典型例题:
题型一、利用等腰三角形的性质进行计算
如图,在ΔABC中,AB=AC,点D,E分别在边AC,AB上,且BC=BD,AD=DE=EB,求∠A的度数.
解题策略利用等腰三角形的性质求角度,若没有已知角度,常通过设未知数,利用“等边对等角”、三角形外角的性质或三角形内角和定理表示相关角,构造方程求解。
变式练习:
如图,在ΔABC中,AB=AC,∠BAC=120°,AD是边BC上的中线,且BD=8B,∠ADE的度数为( )
A.10° B.15° C.20° D.300
2、如图,AB//DE,ΔABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD的度数为( )
A.16° B.28° C.44° D.45°
第1题 第2题
3、如图,∠A=10°,AB=BC=CD=DE=EF,则∠DEF的度数为_________
4、如图,在ΔABC中,∠C=84°,分别以点A,B为圆心,大于AB的长为半径画弧,两弧分别交于点M,N,作直线MN交AC于点D;以点B为圆心,适当长为半径画弧,分别交BA,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线BP,此时射线BP恰好经过点D,则∠A=_________
题型二、利用等腰三角形的性质进行证明
如图,AB=AE,BC=ED,∠B=∠E,AM⊥CD,垂足为M.求证:CM=DM.
“叠合型”等腰三角形的辅助线作法:作底边上的高、作顶角平分线、连接AD并延长
变式练习:
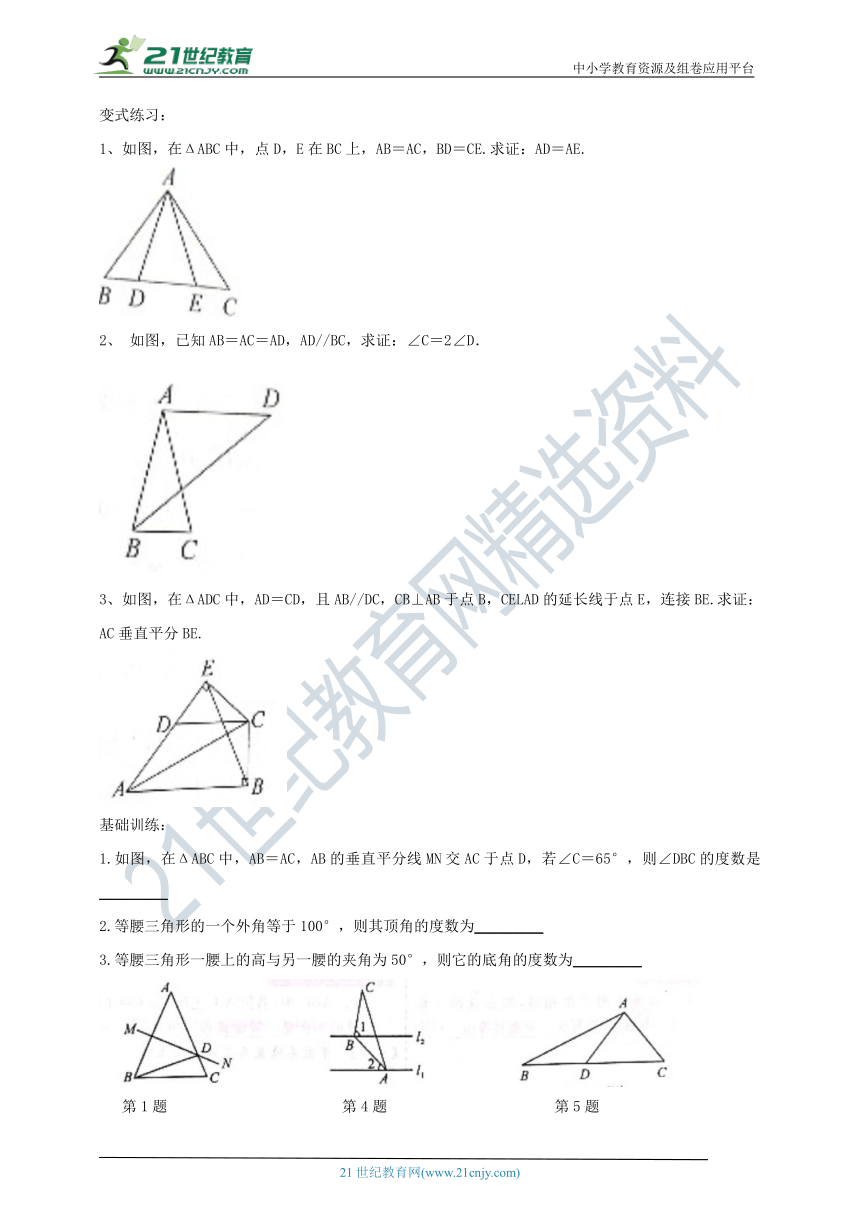
如图,在ΔABC中,点D,E在BC上,AB=AC,BD=CE.求证:AD=AE.
2、 如图,已知AB=AC=AD,AD//BC,求证:∠C=2∠D.
3、如图,在ΔADC中,AD=CD,且AB//DC,CB⊥AB于点B,CELAD的延长线于点E,连接BE.求证:AC垂直平分BE.
基础训练:
1.如图,在ΔABC中,AB=AC,AB的垂直平分线MN交AC于点D,若∠C=65°,则∠DBC的度数是 _________
2.等腰三角形的一个外角等于100°,则其顶角的度数为_________
3.等腰三角形一腰上的高与另一腰的夹角为50°,则它的底角的度数为_________
第1题 第4题 第5题
如图,直线l1//l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=30°,∠1=80°,则∠2的度数为 _________.
5.如图,在ΔABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC的度数为_________
6.如图,在四边形ABCE中,∠E=90°,CA平分∠BCE,AB=AC.求证:BC=2CE.
7.如图,在ΔABC中,AB=BC,F为AC的中点,FD⊥BC于点D,DE⊥AB于点E,直线DE,与AC交于点G.求证:∠ABC=2∠G.
综合题探究
8.如图1,在ΔABC中,点D在边BC上,AB=AD=DC,E为BD的中点.
(1)若∠C=35°,直接写出∠EAD的度数为 _________;
(2)如图2,过点D作DF⊥AD交AC于点F,过点F作FM⊥CD,垂足为M.
①求证:∠EAD=∠FDM;
②求证:AE=DF+FM.
答案版
知识要点:
等腰三角形的两个底角 相等
2.等腰三角形的 顶角平分线 、底边上的高、底边上的中线 相互重合.
3.等腰三角形是 轴对称 图形,其对称轴是底边的垂直平分线.
易错点睛:
等腰三角形的两边长分别为6cm,13cm,其周长为32 cm.
2.已知等腰三角形的一个角为另一个角的2倍,则这角为 36°或90°
典型例题:
题型一、利用等腰三角形的性质进行计算
如图,在ΔABC中,AB=AC,点D,E分别在边AC,AB上,且BC=BD,AD=DE=EB,求∠A的度数.
解:设∠A=x°.
∵AD=DE, ∴∠AED=∠A=x°
∵DE=EB,∠AED=∠EBD+∠BDE,
∴∠EBD=∠BDE=(x)0.
∴∠BDC=∠A+∠EBD=(x)0
∵BC=BD,
∴∠C=∠BDC=(x)0
∵AB=AC,
∴∠ABC=∠C= (x)0
∵∠A+∠ABC+∠C=180°,
∴x+x+x=180,解得x=45.
∴∠A=45°.
解题策略利用等腰三角形的性质求角度,若没有已知角度,常通过设未知数,利用“等边对等角”、三角形外角的性质或三角形内角和定理表示相关角,构造方程求解。
变式练习:
如图,在ΔABC中,AB=AC,∠BAC=120°,AD是边BC上的中线,且BD=8B,∠ADE的度数为(B )
A.10° B.15° C.20° D.300
2、如图,AB//DE,ΔABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD的度数为( C )
A.16° B.28° C.44° D.45°
第1题 第2题
3、如图,∠A=10°,AB=BC=CD=DE=EF,则∠DEF的度数为 100°
4、如图,在ΔABC中,∠C=84°,分别以点A,B为圆心,大于AB的长为半径画弧,两弧分别交于点M,N,作直线MN交AC于点D;以点B为圆心,适当长为半径画弧,分别交BA,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线BP,此时射线BP恰好经过点D,则∠A= 320
题型二、利用等腰三角形的性质进行证明
如图,AB=AE,BC=ED,∠B=∠E,AM⊥CD,垂足为M.求证:CM=DM.
解:如图,连接AC,AD.
在ΔABC和ΔAED中,AB=AE,,∠B=∠E,BC=ED,
∴ΔABC≌ΔAED(SAS).
∴AC=AD.
∵AM⊥CD,
∴CM=DM.
“叠合型”等腰三角形的辅助线作法:作底边上的高、作顶角平分线、连接AD并延长
变式练习:
如图,在ΔABC中,点D,E在BC上,AB=AC,BD=CE.求证:AD=AE.
证明:∵AB=AC. ∴∠B=∠C.
又BD=CE,
∴ΔABD≌ΔACE(SAS)∴AD=AE.
2、 如图,已知AB=AC=AD,AD//BC,求证:∠C=2∠D.
证明:∵AB=AC=AD,
∴∠C=∠ABC,
∠D=∠ABD. ∵AD//BC,∴∠CBD=∠D.
∴∠ABC=∠ABD+∠CBD=2∠D. ∴∠C=2∠D.
3、如图,在ΔADC中,AD=CD,且AB//DC,CB⊥AB于点B,CELAD的延长线于点E,连接BE.求证:AC垂直平分BE.
证明:AD=CD,
∴∠DAC=∠DCA.
∵AB//DC,
∴∠DCA=∠CAB.
∴∠DAC=∠CAB.
∵CE⊥AE,CB⊥AB,
∴∠CEA=∠CBA=90°,CE=CB.
∴点C在线段BE的垂直平分线上.
在RtΔCEA和RtΔCBA中,
AC=AC,
CE=CB,
∴RtΔCEA≌RtΔCBA(HL).
∴AE=AB.∴点A在线段BE的垂直平分线上。
∴AC垂直平分BE.
基础训练:
1.如图,在ΔABC中,AB=AC,AB的垂直平分线MN交AC于点D,若∠C=65°,则∠DBC的度数是 15°
2.等腰三角形的一个外角等于100°,则其顶角的度数为 20°或80°
3.等腰三角形一腰上的高与另一腰的夹角为50°,则它的底角的度数为 70°或20°
第1题 第4题 第5题
如图,直线l1//l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=30°,∠1=80°,则∠2的度数为 40°.
5.如图,在ΔABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC的度数为 52°
6.如图,在四边形ABCE中,∠E=90°,CA平分∠BCE,AB=AC.求证:BC=2CE.
证明:过点A作AD⊥BC于点D,证ΔADC≌ΔAEC,BC=2CD=2CE.
7.如图,在ΔABC中,AB=BC,F为AC的中点,FD⊥BC于点D,DE⊥AB于点E,直线DE,与AC交于点G.求证:∠ABC=2∠G.
证明:连接BF.
∵AB=BC,F为AC的中点,
∴BF⊥AC,∠ABC=2∠ABF.
∴∠A+∠ABF=90°∵DE⊥AB,∠A+∠G=90°. ∵∠G=∠ABF,∴∠ABC=2∠G.
综合题探究
8.如图1,在ΔABC中,点D在边BC上,AB=AD=DC,E为BD的中点.
(1)若∠C=35°,直接写出∠EAD的度数为 20°;
(2)如图2,过点D作DF⊥AD交AC于点F,过点F作FM⊥CD,垂足为M.
①求证:∠EAD=∠FDM;
②求证:AE=DF+FM.
解:(1)20°;
(2)①证明:∵AB=AD,E为BD的中点,
∴AE⊥BC,∴∠EAD+∠ADE=90°.
∵AD⊥DF,∴∠ADF=90°,∴∠FDM+∠ADE=90°∴∠EAD=∠FDM;
②证明:法一,在AE上截取AN=DF,连接DN.
∵∠EAD=∠FDM,AD=DC,
∴ΔAND≌ΔDFC,∠ADN=∠C,DN=FC,∠ADN=∠C=∠DAC...DN//AC,
∴∠NDE=∠C.∵AE⊥BC,FM⊥BC,∴ΔNDE≌ΔFCM,
∴NE=FM.∴AE=AN+NE=DF+FM.
法二,过点C作CH⊥DF交DF的延长线于点H,易证CH//AD.
∴∠HCF=∠DAC=∠ACB.∵FM⊥BC,CH⊥DH∵FM=FH.
易证ΔADE≌ΔDCH,∴AE=DH=DF+FH=DF+FM.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
13.3等腰三角形
第1课时 等腰三角形的性质
知识要点:
等腰三角形的两个底角_________
2.等腰三角形的 __________ 、_________、_________ 相互重合.
3.等腰三角形是_________ 图形,其对称轴是__________________.
易错点睛:
等腰三角形的两边长分别为6cm,13cm,其周长为_________
2.已知等腰三角形的一个角为另一个角的2倍,则这角为 __________________
典型例题:
题型一、利用等腰三角形的性质进行计算
如图,在ΔABC中,AB=AC,点D,E分别在边AC,AB上,且BC=BD,AD=DE=EB,求∠A的度数.
解题策略利用等腰三角形的性质求角度,若没有已知角度,常通过设未知数,利用“等边对等角”、三角形外角的性质或三角形内角和定理表示相关角,构造方程求解。
变式练习:
如图,在ΔABC中,AB=AC,∠BAC=120°,AD是边BC上的中线,且BD=8B,∠ADE的度数为( )
A.10° B.15° C.20° D.300
2、如图,AB//DE,ΔABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD的度数为( )
A.16° B.28° C.44° D.45°
第1题 第2题
3、如图,∠A=10°,AB=BC=CD=DE=EF,则∠DEF的度数为_________
4、如图,在ΔABC中,∠C=84°,分别以点A,B为圆心,大于AB的长为半径画弧,两弧分别交于点M,N,作直线MN交AC于点D;以点B为圆心,适当长为半径画弧,分别交BA,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线BP,此时射线BP恰好经过点D,则∠A=_________
题型二、利用等腰三角形的性质进行证明
如图,AB=AE,BC=ED,∠B=∠E,AM⊥CD,垂足为M.求证:CM=DM.
“叠合型”等腰三角形的辅助线作法:作底边上的高、作顶角平分线、连接AD并延长
变式练习:
如图,在ΔABC中,点D,E在BC上,AB=AC,BD=CE.求证:AD=AE.
2、 如图,已知AB=AC=AD,AD//BC,求证:∠C=2∠D.
3、如图,在ΔADC中,AD=CD,且AB//DC,CB⊥AB于点B,CELAD的延长线于点E,连接BE.求证:AC垂直平分BE.
基础训练:
1.如图,在ΔABC中,AB=AC,AB的垂直平分线MN交AC于点D,若∠C=65°,则∠DBC的度数是 _________
2.等腰三角形的一个外角等于100°,则其顶角的度数为_________
3.等腰三角形一腰上的高与另一腰的夹角为50°,则它的底角的度数为_________
第1题 第4题 第5题
如图,直线l1//l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=30°,∠1=80°,则∠2的度数为 _________.
5.如图,在ΔABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC的度数为_________
6.如图,在四边形ABCE中,∠E=90°,CA平分∠BCE,AB=AC.求证:BC=2CE.
7.如图,在ΔABC中,AB=BC,F为AC的中点,FD⊥BC于点D,DE⊥AB于点E,直线DE,与AC交于点G.求证:∠ABC=2∠G.
综合题探究
8.如图1,在ΔABC中,点D在边BC上,AB=AD=DC,E为BD的中点.
(1)若∠C=35°,直接写出∠EAD的度数为 _________;
(2)如图2,过点D作DF⊥AD交AC于点F,过点F作FM⊥CD,垂足为M.
①求证:∠EAD=∠FDM;
②求证:AE=DF+FM.
答案版
知识要点:
等腰三角形的两个底角 相等
2.等腰三角形的 顶角平分线 、底边上的高、底边上的中线 相互重合.
3.等腰三角形是 轴对称 图形,其对称轴是底边的垂直平分线.
易错点睛:
等腰三角形的两边长分别为6cm,13cm,其周长为32 cm.
2.已知等腰三角形的一个角为另一个角的2倍,则这角为 36°或90°
典型例题:
题型一、利用等腰三角形的性质进行计算
如图,在ΔABC中,AB=AC,点D,E分别在边AC,AB上,且BC=BD,AD=DE=EB,求∠A的度数.
解:设∠A=x°.
∵AD=DE, ∴∠AED=∠A=x°
∵DE=EB,∠AED=∠EBD+∠BDE,
∴∠EBD=∠BDE=(x)0.
∴∠BDC=∠A+∠EBD=(x)0
∵BC=BD,
∴∠C=∠BDC=(x)0
∵AB=AC,
∴∠ABC=∠C= (x)0
∵∠A+∠ABC+∠C=180°,
∴x+x+x=180,解得x=45.
∴∠A=45°.
解题策略利用等腰三角形的性质求角度,若没有已知角度,常通过设未知数,利用“等边对等角”、三角形外角的性质或三角形内角和定理表示相关角,构造方程求解。
变式练习:
如图,在ΔABC中,AB=AC,∠BAC=120°,AD是边BC上的中线,且BD=8B,∠ADE的度数为(B )
A.10° B.15° C.20° D.300
2、如图,AB//DE,ΔABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD的度数为( C )
A.16° B.28° C.44° D.45°
第1题 第2题
3、如图,∠A=10°,AB=BC=CD=DE=EF,则∠DEF的度数为 100°
4、如图,在ΔABC中,∠C=84°,分别以点A,B为圆心,大于AB的长为半径画弧,两弧分别交于点M,N,作直线MN交AC于点D;以点B为圆心,适当长为半径画弧,分别交BA,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线BP,此时射线BP恰好经过点D,则∠A= 320
题型二、利用等腰三角形的性质进行证明
如图,AB=AE,BC=ED,∠B=∠E,AM⊥CD,垂足为M.求证:CM=DM.
解:如图,连接AC,AD.
在ΔABC和ΔAED中,AB=AE,,∠B=∠E,BC=ED,
∴ΔABC≌ΔAED(SAS).
∴AC=AD.
∵AM⊥CD,
∴CM=DM.
“叠合型”等腰三角形的辅助线作法:作底边上的高、作顶角平分线、连接AD并延长
变式练习:
如图,在ΔABC中,点D,E在BC上,AB=AC,BD=CE.求证:AD=AE.
证明:∵AB=AC. ∴∠B=∠C.
又BD=CE,
∴ΔABD≌ΔACE(SAS)∴AD=AE.
2、 如图,已知AB=AC=AD,AD//BC,求证:∠C=2∠D.
证明:∵AB=AC=AD,
∴∠C=∠ABC,
∠D=∠ABD. ∵AD//BC,∴∠CBD=∠D.
∴∠ABC=∠ABD+∠CBD=2∠D. ∴∠C=2∠D.
3、如图,在ΔADC中,AD=CD,且AB//DC,CB⊥AB于点B,CELAD的延长线于点E,连接BE.求证:AC垂直平分BE.
证明:AD=CD,
∴∠DAC=∠DCA.
∵AB//DC,
∴∠DCA=∠CAB.
∴∠DAC=∠CAB.
∵CE⊥AE,CB⊥AB,
∴∠CEA=∠CBA=90°,CE=CB.
∴点C在线段BE的垂直平分线上.
在RtΔCEA和RtΔCBA中,
AC=AC,
CE=CB,
∴RtΔCEA≌RtΔCBA(HL).
∴AE=AB.∴点A在线段BE的垂直平分线上。
∴AC垂直平分BE.
基础训练:
1.如图,在ΔABC中,AB=AC,AB的垂直平分线MN交AC于点D,若∠C=65°,则∠DBC的度数是 15°
2.等腰三角形的一个外角等于100°,则其顶角的度数为 20°或80°
3.等腰三角形一腰上的高与另一腰的夹角为50°,则它的底角的度数为 70°或20°
第1题 第4题 第5题
如图,直线l1//l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=30°,∠1=80°,则∠2的度数为 40°.
5.如图,在ΔABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC的度数为 52°
6.如图,在四边形ABCE中,∠E=90°,CA平分∠BCE,AB=AC.求证:BC=2CE.
证明:过点A作AD⊥BC于点D,证ΔADC≌ΔAEC,BC=2CD=2CE.
7.如图,在ΔABC中,AB=BC,F为AC的中点,FD⊥BC于点D,DE⊥AB于点E,直线DE,与AC交于点G.求证:∠ABC=2∠G.
证明:连接BF.
∵AB=BC,F为AC的中点,
∴BF⊥AC,∠ABC=2∠ABF.
∴∠A+∠ABF=90°∵DE⊥AB,∠A+∠G=90°. ∵∠G=∠ABF,∴∠ABC=2∠G.
综合题探究
8.如图1,在ΔABC中,点D在边BC上,AB=AD=DC,E为BD的中点.
(1)若∠C=35°,直接写出∠EAD的度数为 20°;
(2)如图2,过点D作DF⊥AD交AC于点F,过点F作FM⊥CD,垂足为M.
①求证:∠EAD=∠FDM;
②求证:AE=DF+FM.
解:(1)20°;
(2)①证明:∵AB=AD,E为BD的中点,
∴AE⊥BC,∴∠EAD+∠ADE=90°.
∵AD⊥DF,∴∠ADF=90°,∴∠FDM+∠ADE=90°∴∠EAD=∠FDM;
②证明:法一,在AE上截取AN=DF,连接DN.
∵∠EAD=∠FDM,AD=DC,
∴ΔAND≌ΔDFC,∠ADN=∠C,DN=FC,∠ADN=∠C=∠DAC...DN//AC,
∴∠NDE=∠C.∵AE⊥BC,FM⊥BC,∴ΔNDE≌ΔFCM,
∴NE=FM.∴AE=AN+NE=DF+FM.
法二,过点C作CH⊥DF交DF的延长线于点H,易证CH//AD.
∴∠HCF=∠DAC=∠ACB.∵FM⊥BC,CH⊥DH∵FM=FH.
易证ΔADE≌ΔDCH,∴AE=DH=DF+FH=DF+FM.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
