2012高一物理课件:第四章 第三节 探究外力做功与物体动能变化的关系 (粤教版必修2)
文档属性
| 名称 | 2012高一物理课件:第四章 第三节 探究外力做功与物体动能变化的关系 (粤教版必修2) |  | |
| 格式 | zip | ||
| 文件大小 | 352.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 广东版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-08-27 21:12:25 | ||
图片预览






文档简介
(共20张PPT)
第三节 探究外力做功与物体动能变化的关系
动能定理
合外力
动能
1.动能定理:_______对物体所做的功等于物体______的
变化.
Ek2-Ek1
ΔEk
2.表达式:W=________或 W=_______.
3.当外力对物体做正功时,末动能_______初动能;当外
力对物体做负功时,末动能______初动能.
大于
小于
4.合外力做的功
(1)包括重力在内的所有外力做的功.
(2)W0=W1+W2+…+Wn,W0为合力做的功,Wn(n=1,2,
…)为分力做的功.
要点1
动能定理的实验探究
1.实验研究:探究外力做功与物体动能变化的关系
(1)实验器材:电火花打点计时器、纸带、重锤、铁架台、
钩码、夹子、刻度尺、学生电源、导线若干.
(2)实验步骤:
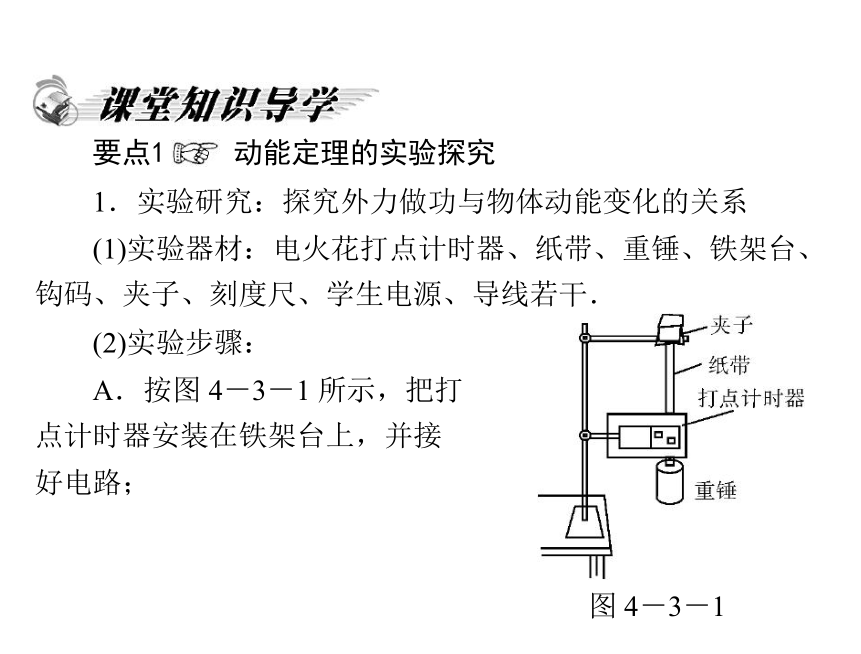
A.按图 4-3-1 所示,把打
点计时器安装在铁架台上,并接
好电路;
图 4-3-1
F.利用公式vn=
B.纸带的一端用夹子固定在重锤上,另一端穿过打点计
时器的限位孔,竖直提起纸带使重锤靠近打点计时器,用夹子
把纸带上端夹住;
C.先接通打点计时器的电源,待稳定后,释放纸带,让
重锤自由下落,打点计时器在纸带上打点;
D.重复几次(3~5 次),挑选出点迹清晰的纸带用来分析;
E.在选取纸带中,选取点迹间距较大的点,并标上 0、1、
2、3、4、…,量出各点到 0 点的距离 h1、h2、h3、…;
求出各点的速度大小;
G.并求出相邻两点间重锤动能的增量ΔEk 和重锤重力做的
功 W;
H.比较重力所做的功 W 和动能增量ΔEk 的关系,得出结
论.
结论:在误差范围内,重力所做的功等于物体动能的增量.
2.理论分析与论证
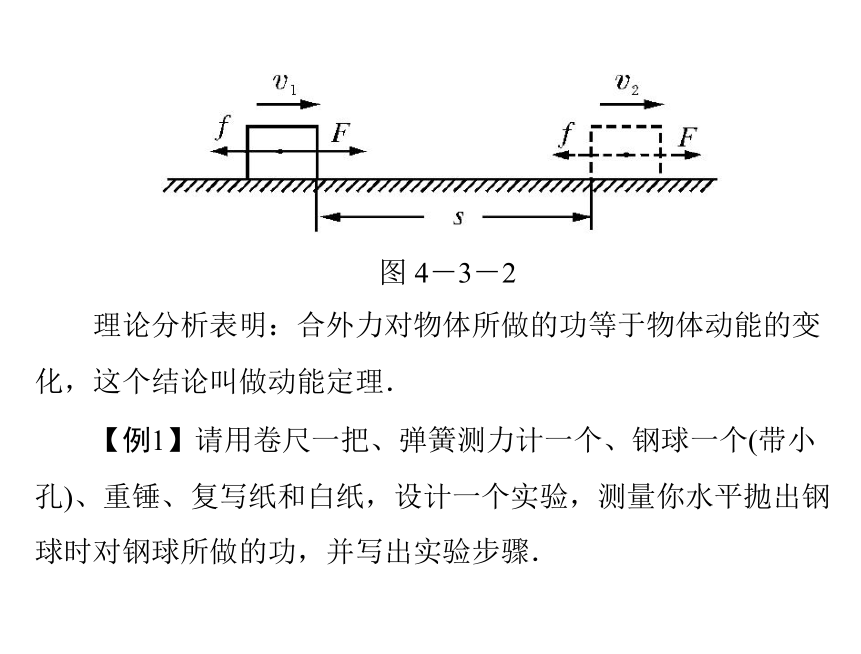
如图 4-3-2 所示,设物体的质量为 m,在与运动方向相
同的恒定外力 F 的作用下发生一段位移 s,速度由 v1 增加到 v2,
已知物体与水平面间的摩擦力恒为 f,由牛顿定律得 W合=F合 s
图 4-3-2
理论分析表明:合外力对物体所做的功等于物体动能的变
化,这个结论叫做动能定理.
【例1】请用卷尺一把、弹簧测力计一个、钢球一个(带小
孔)、重锤、复写纸和白纸,设计一个实验,测量你水平抛出钢
球时对钢球所做的功,并写出实验步骤.
解析:用卷尺可测出钢球抛出点与落地点的水平距离和竖
直高度;根据平抛运动的规律可求得抛出点的初速度;由动能
定理,可求得对钢球所做的功.
答案:(1)将钢球用手固定在某一位置,用力将钢球水平推
出,观察钢球落地点的大概位置;
(2)在钢球落地点的大概位置上铺一张白纸,在白纸上方铺
上复写纸并固定;
(3)重复步骤(1)多次(5~10 次);
(4)取开复写纸,白纸位置固定,在小球落在白纸上留下的
痕迹中作一外切圆,标出外切圆的圆心;
(5)在钢球抛出点悬挂重锤,用卷尺沿铅垂线方向测出钢球
抛出点离地面的高度 h,并用卷尺测出重锤在地面的投影点与
外切圆圆心的距离 s,即钢球做平抛运动的水平距离;
(6)用弹簧测力计悬挂钢球使之处于静止状态,读出测力计
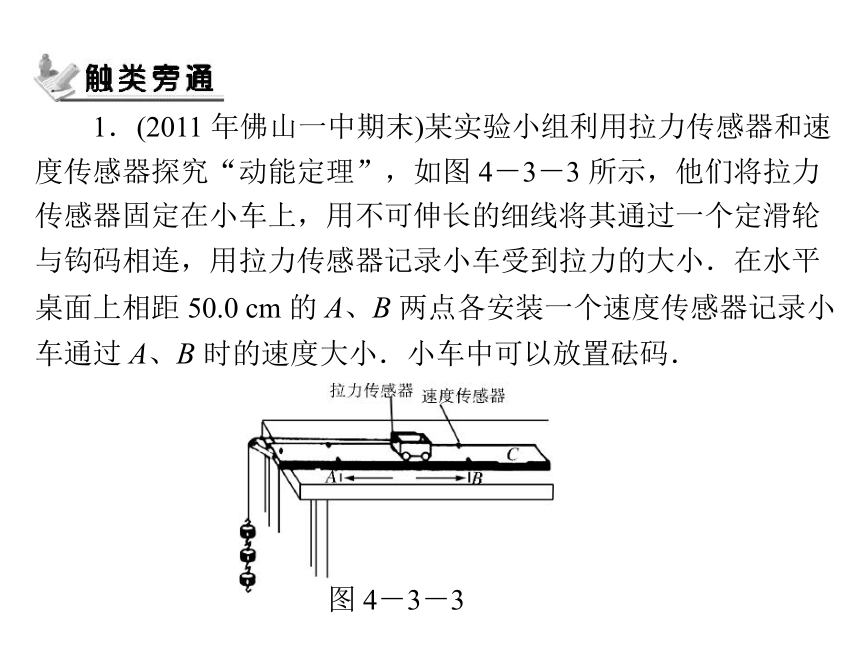
1.(2011 年佛山一中期末)某实验小组利用拉力传感器和速
度传感器探究“动能定理”,如图 4-3-3 所示,他们将拉力
传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮
与钩码相连,用拉力传感器记录小车受到拉力的大小.在水平
桌面上相距 50.0 cm 的 A、B 两点各安装一个速度传感器记录小
车通过 A、B 时的速度大小.小车中可以放置砝码.
图 4-3-3
(1)实验主要步骤如下:
①测量小车和拉力传感器的总质量 M1,把细线的一端固定
在拉力传感器上,另一端通过定滑轮与钩码相连,正确连接所
需电路;
②将小车停在 C 点,然后释放小车,小车在细线拉动下运
动,记录(
)
A
A.细线拉力及小车通过 A、B 时的速度
B.钩码的质量和小车的质量
C.钩码的质量及小车通过 A、B 时的速度
D.小车的质量和细线的长度
③在小车中增加砝码,或减少砝码,重复步骤②的操作.
次数 M/kg ΔE/J F/N W/J
1 0.500 0.760 0.190 0.400 0.200
2 0.500 1.65 0.413 0.840 0.420
3 0.500 2.40 ΔE3 1.220 W3
4 1.000 2.40 1.20 2.420 1.21
5 1.000 2.84 1.42 2.860 1.43
0.600
0.610
果保留三位有效数字)
表 1 数据记录表
(2)表1是他们测得的一组数据,其中M是M1与小车中砝码质量m之和, 是两个速度传感器记录速度的平方差,可以据此计算出动能变化量ΔE,F是拉力传感器受到的拉力,W是F在A、B间所做的功.表格中ΔE3=_______,W3=_____
(3)根据表 1 提供的数据,请在图 4-3-4 中作出ΔE-W 图线.
图 10
图 4-3-4
解:如图10 所示
要点2
动能定理的理解与应用
1.对动能定理的理解
(1)W 为物体所受外力的总功(包括物体所受重力).
(2)动能定理揭示了合外力对物体做功与物体动能的变化
之间的因果联系和定量关系.定理表明,合外力对物体做了多
少功,物体的动能就增加(减少)多少.合外力做正功,物体的
动能增加;合外力做负功,物体的动能减少.
(3)适用条件:动能定理虽然是在物体受恒力作用沿直线做
匀加速直线运动的情况下推导出来的,但是对于外力是变力或
物体做曲线运动,动能定理都成立.
2.优越性
(1)对于变力作用或曲线运动,动能定理提供了一种计算变
力做功的简便方法.功的计算公式 W=Fscos α只能求恒力做的
功,不能求变力做的功,而由于动能定理提供了一个物体的动
能变化ΔEk 与合外力对物体所做功具有等量代换关系,因此已
知(或求出)物体动能变化ΔEk=Ek2-Ek1,就可以间接求得变力
做的功.
牛顿定律 动能定理
不
同
点 适用条件 一般只能研究在恒力
作用下物体做直线运
动的情况 对于物体在恒力或变力作
用下,物体做直线或曲线
运动均适用
应用方法 要考虑运动过程的每
一个细节,结合运动
学公式解题 只考虑各力的做功情况及
初、末状态的动能
运算方法 矢量运算 代数运算
相同点 确定研究对象,对物体进行受力分析和运动过程
分析
(2)与用牛顿定律解题的比较
3.运用动能定理解题的一般步骤
(1)明确研究对象和运动过程.
(2)分析过程中力做功情况.
(3)明确初、末状态的动能.
(4)列方程,并求解.
【例2】一铅球运动员,奋力一推,将 8 kg 的铅球推出 10 m
远.铅球落地后将地面击出一坑,有经验的专家根据坑的深度
形状认为铅球落地的速度大约是 12 m/s.若铅球出手时的高度是
2 m,求推球过程中运动员对球做的功大约是多少?(g 取 10 m/s2)
解:方法一:分段法
设铅球出手时的速度大小是v0,铅球从出手到落地这一过
程中只有重力对铅球做功,根据动能定理有
对运动员推铅球的过程应用动能定理,推力是对铅球的合
力,则人对球做的功为
代入数据解得W人=416 J.
方法二:全过程法
对人开始推铅球到铅球落地整个过程应用动能定理得
2.如图 4-3-5 所示,在高为 H 的平台上以初速 v0 抛出
一个质量为 m 的小球,不计空气阻力,当它到达离抛出点的竖
)
D
直距离为 h 的 B 点时,小球的动能增量为(
图 4-3-5
3.一个质量为 m 的小球,用长为 l 的轻绳悬挂于 O 点,
小球在水平拉力 F 作用下,从平衡位置 P 点很缓慢地移动到 Q
点,如图 4-3-6 所示,则拉力 F 所做的功为(
)
C
A.mglcos θ
B.Flcos θ
C.mgl(1-cos θ)
D.mglcos θ
解析:题中“很缓慢地移动”的隐含条件是速度大小不变,
由动能定理有WF-mgl(1-cos θ)=0,WF=mgl(1-cos θ).
图 4-3-6
第三节 探究外力做功与物体动能变化的关系
动能定理
合外力
动能
1.动能定理:_______对物体所做的功等于物体______的
变化.
Ek2-Ek1
ΔEk
2.表达式:W=________或 W=_______.
3.当外力对物体做正功时,末动能_______初动能;当外
力对物体做负功时,末动能______初动能.
大于
小于
4.合外力做的功
(1)包括重力在内的所有外力做的功.
(2)W0=W1+W2+…+Wn,W0为合力做的功,Wn(n=1,2,
…)为分力做的功.
要点1
动能定理的实验探究
1.实验研究:探究外力做功与物体动能变化的关系
(1)实验器材:电火花打点计时器、纸带、重锤、铁架台、
钩码、夹子、刻度尺、学生电源、导线若干.
(2)实验步骤:
A.按图 4-3-1 所示,把打
点计时器安装在铁架台上,并接
好电路;
图 4-3-1
F.利用公式vn=
B.纸带的一端用夹子固定在重锤上,另一端穿过打点计
时器的限位孔,竖直提起纸带使重锤靠近打点计时器,用夹子
把纸带上端夹住;
C.先接通打点计时器的电源,待稳定后,释放纸带,让
重锤自由下落,打点计时器在纸带上打点;
D.重复几次(3~5 次),挑选出点迹清晰的纸带用来分析;
E.在选取纸带中,选取点迹间距较大的点,并标上 0、1、
2、3、4、…,量出各点到 0 点的距离 h1、h2、h3、…;
求出各点的速度大小;
G.并求出相邻两点间重锤动能的增量ΔEk 和重锤重力做的
功 W;
H.比较重力所做的功 W 和动能增量ΔEk 的关系,得出结
论.
结论:在误差范围内,重力所做的功等于物体动能的增量.
2.理论分析与论证
如图 4-3-2 所示,设物体的质量为 m,在与运动方向相
同的恒定外力 F 的作用下发生一段位移 s,速度由 v1 增加到 v2,
已知物体与水平面间的摩擦力恒为 f,由牛顿定律得 W合=F合 s
图 4-3-2
理论分析表明:合外力对物体所做的功等于物体动能的变
化,这个结论叫做动能定理.
【例1】请用卷尺一把、弹簧测力计一个、钢球一个(带小
孔)、重锤、复写纸和白纸,设计一个实验,测量你水平抛出钢
球时对钢球所做的功,并写出实验步骤.
解析:用卷尺可测出钢球抛出点与落地点的水平距离和竖
直高度;根据平抛运动的规律可求得抛出点的初速度;由动能
定理,可求得对钢球所做的功.
答案:(1)将钢球用手固定在某一位置,用力将钢球水平推
出,观察钢球落地点的大概位置;
(2)在钢球落地点的大概位置上铺一张白纸,在白纸上方铺
上复写纸并固定;
(3)重复步骤(1)多次(5~10 次);
(4)取开复写纸,白纸位置固定,在小球落在白纸上留下的
痕迹中作一外切圆,标出外切圆的圆心;
(5)在钢球抛出点悬挂重锤,用卷尺沿铅垂线方向测出钢球
抛出点离地面的高度 h,并用卷尺测出重锤在地面的投影点与
外切圆圆心的距离 s,即钢球做平抛运动的水平距离;
(6)用弹簧测力计悬挂钢球使之处于静止状态,读出测力计
1.(2011 年佛山一中期末)某实验小组利用拉力传感器和速
度传感器探究“动能定理”,如图 4-3-3 所示,他们将拉力
传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮
与钩码相连,用拉力传感器记录小车受到拉力的大小.在水平
桌面上相距 50.0 cm 的 A、B 两点各安装一个速度传感器记录小
车通过 A、B 时的速度大小.小车中可以放置砝码.
图 4-3-3
(1)实验主要步骤如下:
①测量小车和拉力传感器的总质量 M1,把细线的一端固定
在拉力传感器上,另一端通过定滑轮与钩码相连,正确连接所
需电路;
②将小车停在 C 点,然后释放小车,小车在细线拉动下运
动,记录(
)
A
A.细线拉力及小车通过 A、B 时的速度
B.钩码的质量和小车的质量
C.钩码的质量及小车通过 A、B 时的速度
D.小车的质量和细线的长度
③在小车中增加砝码,或减少砝码,重复步骤②的操作.
次数 M/kg ΔE/J F/N W/J
1 0.500 0.760 0.190 0.400 0.200
2 0.500 1.65 0.413 0.840 0.420
3 0.500 2.40 ΔE3 1.220 W3
4 1.000 2.40 1.20 2.420 1.21
5 1.000 2.84 1.42 2.860 1.43
0.600
0.610
果保留三位有效数字)
表 1 数据记录表
(2)表1是他们测得的一组数据,其中M是M1与小车中砝码质量m之和, 是两个速度传感器记录速度的平方差,可以据此计算出动能变化量ΔE,F是拉力传感器受到的拉力,W是F在A、B间所做的功.表格中ΔE3=_______,W3=_____
(3)根据表 1 提供的数据,请在图 4-3-4 中作出ΔE-W 图线.
图 10
图 4-3-4
解:如图10 所示
要点2
动能定理的理解与应用
1.对动能定理的理解
(1)W 为物体所受外力的总功(包括物体所受重力).
(2)动能定理揭示了合外力对物体做功与物体动能的变化
之间的因果联系和定量关系.定理表明,合外力对物体做了多
少功,物体的动能就增加(减少)多少.合外力做正功,物体的
动能增加;合外力做负功,物体的动能减少.
(3)适用条件:动能定理虽然是在物体受恒力作用沿直线做
匀加速直线运动的情况下推导出来的,但是对于外力是变力或
物体做曲线运动,动能定理都成立.
2.优越性
(1)对于变力作用或曲线运动,动能定理提供了一种计算变
力做功的简便方法.功的计算公式 W=Fscos α只能求恒力做的
功,不能求变力做的功,而由于动能定理提供了一个物体的动
能变化ΔEk 与合外力对物体所做功具有等量代换关系,因此已
知(或求出)物体动能变化ΔEk=Ek2-Ek1,就可以间接求得变力
做的功.
牛顿定律 动能定理
不
同
点 适用条件 一般只能研究在恒力
作用下物体做直线运
动的情况 对于物体在恒力或变力作
用下,物体做直线或曲线
运动均适用
应用方法 要考虑运动过程的每
一个细节,结合运动
学公式解题 只考虑各力的做功情况及
初、末状态的动能
运算方法 矢量运算 代数运算
相同点 确定研究对象,对物体进行受力分析和运动过程
分析
(2)与用牛顿定律解题的比较
3.运用动能定理解题的一般步骤
(1)明确研究对象和运动过程.
(2)分析过程中力做功情况.
(3)明确初、末状态的动能.
(4)列方程,并求解.
【例2】一铅球运动员,奋力一推,将 8 kg 的铅球推出 10 m
远.铅球落地后将地面击出一坑,有经验的专家根据坑的深度
形状认为铅球落地的速度大约是 12 m/s.若铅球出手时的高度是
2 m,求推球过程中运动员对球做的功大约是多少?(g 取 10 m/s2)
解:方法一:分段法
设铅球出手时的速度大小是v0,铅球从出手到落地这一过
程中只有重力对铅球做功,根据动能定理有
对运动员推铅球的过程应用动能定理,推力是对铅球的合
力,则人对球做的功为
代入数据解得W人=416 J.
方法二:全过程法
对人开始推铅球到铅球落地整个过程应用动能定理得
2.如图 4-3-5 所示,在高为 H 的平台上以初速 v0 抛出
一个质量为 m 的小球,不计空气阻力,当它到达离抛出点的竖
)
D
直距离为 h 的 B 点时,小球的动能增量为(
图 4-3-5
3.一个质量为 m 的小球,用长为 l 的轻绳悬挂于 O 点,
小球在水平拉力 F 作用下,从平衡位置 P 点很缓慢地移动到 Q
点,如图 4-3-6 所示,则拉力 F 所做的功为(
)
C
A.mglcos θ
B.Flcos θ
C.mgl(1-cos θ)
D.mglcos θ
解析:题中“很缓慢地移动”的隐含条件是速度大小不变,
由动能定理有WF-mgl(1-cos θ)=0,WF=mgl(1-cos θ).
图 4-3-6
同课章节目录
- 第一章 抛体运动
- 第01节 什么是抛体运动
- 第02节 运动的合成与分解
- 第03节 竖直方向的抛体运动
- 第04节 平抛运动
- 第05节 斜抛运动
- 第二章 圆周运动
- 第01节 匀速圆周运动
- 第02节 向心力
- 第03节 离心现象及其应用
- 第三章 万有引力定律及其应用
- 第01节 万有引力定律
- 第02节 万有引力定律的应用
- 第03节 飞向太空
- 第四章 机械能和能源
- 第01节 功
- 第02节 动能 势能
- 第03节 探究外力做功与物体动能变化的关系
- 第04节 机械能守恒定律
- 第05节 验证机械能守恒定律
- 第06节 能量 能量转化与守恒定律
- 第07节 功率
- 第08节 能源的开发与利用
- 第五章 经典力学与物理学的革命
- 第01节 经典力学的成就与局限性
- 第02节 经典时空观与相对论时空观
- 第03节 量子化现象
- 第04节 物理学——人类文明进步的阶梯
