2012高一物理课件:第四章 第四节 机械能守恒定律 (粤教版必修2)
文档属性
| 名称 | 2012高一物理课件:第四章 第四节 机械能守恒定律 (粤教版必修2) |  | |
| 格式 | zip | ||
| 文件大小 | 250.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 广东版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-08-27 21:12:25 | ||
图片预览







文档简介
(共21张PPT)
第四节 机械能守恒定律
一、动能与势能之间的相互转化
1.机械能:______与势能(包括__________和__________),
统称为机械能.
动能
重力势能
弹性势能
2.动能和势能的相互转化是通过______或______做功来实
现的.
重力
弹力
蹦极是非常刺激的户外休闲活动,深受年轻人的喜爱.跳
跃者站在约 40 米以上高度的桥梁、塔顶、高楼甚至热气球上.
人在蹦极时可在空中享受几秒钟的“自由落体”.当人体下落
到一定高度时,橡皮绳被拉开、绷紧,阻止人体
继续下落,当到达最低点时橡皮绳再次弹起,人
被拉起,随后,又落下,这样反复多次直到橡皮
绳的弹性消失为止,这就是蹦极的全过程.
你能简单说说人从最高处下落到最低点时
的能量转化过程吗?
图 4-4-1
答案:人从最高点下落到绳恰好伸直的过程:重力势能转
化为动能.从绳恰好伸直到绳的弹力 F=mg 的过程:重力势能
转化为动能和弹性势能.从绳的弹力 F=mg 到最低点的过程中:
重力势能和动能转化为弹性势能.整个过程可看成重力势能与
弹性势能间的相互转化.
二、机械能守恒定律
1.机械能守恒定律:在只有重力(或弹力)做功的情形下,
物体的动能和____________(或弹性势能)发生相互转化,而总
的机械能保持不变.
重力势能
Ek2+Ep2
2.表达式:Ek1+Ep1=__________或ΔEp+ΔEk=0.
要点1
机械能是否守恒的判断
1.从能量特点看:只有系统动能和势能相互转化,无其他
形式能量之间(如内能)转化,则系统机械能守恒.如果物体间
发生相互碰撞或相对运动,又有相互间的摩擦作用时有内能的
增加,机械能一般不守恒.
2.从机械能的定义看:若动能与势能之和不变化,则机械
能守恒.如果一个物体沿斜面匀速(或减速)滑下,动能不变(或
减小),势能减小,则机械能减小;一个物体沿水平方向匀速运
动时机械能守恒,沿竖直方向匀速运动时机械能不守恒.
3.从做功特点看:只有重力和系统内的弹力做功,系统机
械能守恒.具体表现在:
(1)只受重力(或系统内的弹力)作用.如:所有做抛体运动
的物体(不计阻力).
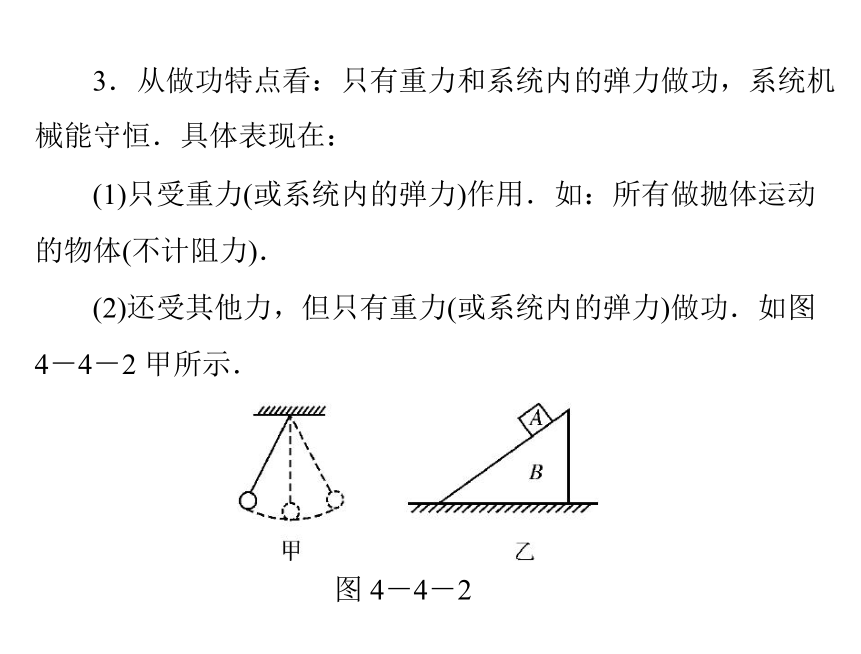
(2)还受其他力,但只有重力(或系统内的弹力)做功.如图
4-4-2 甲所示.
图 4-4-2
(3)有系统的内力做功,但是做功代数和为零.如图 4-4
-2 乙所示,A、B 间及 B 与地面之间均光滑,A 自 B 的上端自
由下滑时,B 沿地面滑动,A、B 之间的弹力做功,对 A 或 B 机
械能均不守恒,但对 A、B 组成的系统机械能守恒.
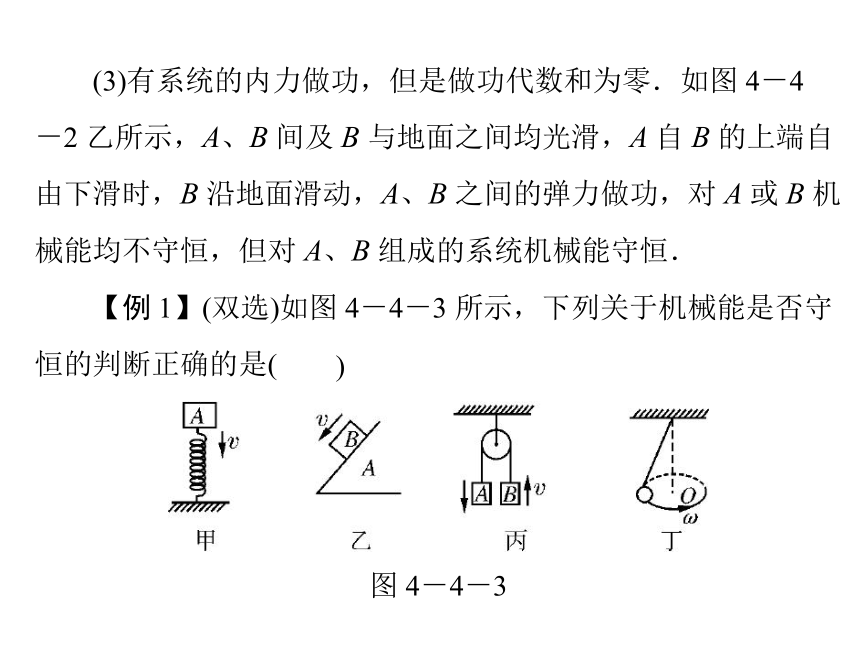
【例 1】(双选)如图 4-4-3 所示,下列关于机械能是否守
恒的判断正确的是(
)
图 4-4-3
A.甲图中,物体 A 将弹簧压缩的过程中,A 机械能守恒
B.乙图中,A 置于光滑水平面,物体 B 沿光滑斜面下滑,
物体 B 机械能守恒
C.丙图中,不计任何阻力时,A 加速下落,B 加速上升过
程中,A、B 组成的系统机械能守恒
D.丁图中,小球沿水平面做匀速圆锥摆运动时,小球的
机械能守恒
解析:甲图中,重力和弹力做功,物体 A 和弹簧组成的系
统机械能守恒,但物体 A 机械能不守恒,选项 A 错;乙图中,
物体 B 除受重力外,还受弹力,弹力对 B 做负功,机械能不守
恒,但从能量特点看,A、B 组成的系统机械能守恒,B 错;丙
图中,绳子张力对 A 做负功,对 B 做正功,代数和为零,A、
B 组成的系统机械能守恒,C 对;丁图中动能不变,势能不变,
机械能守恒,D 对.
答案:CD
1.(双选,2011 年东山中学期末)关于机械能是否守恒,下
列叙述中正确的是(
)
BD
A.做匀速直线运动的物体的机械能一定守恒
B.做匀变速运动的物体的机械能可能守恒
C.外力对物体做功为零时,机械能一定守恒
D.只有重力对物体做功,物体机械能一定守恒
要点2
机械能守恒定律的运用
1.机械能守恒定律的三种表达式
(1)Ek1+Ep1=Ek2+Ep2,即初状态的动能与势能之和等于末
状态的动能与势能之和,选用该表达式时,应恰当选取参考平面.
(2)ΔEk=-ΔEp 或ΔEp=-ΔEk,即动能(或势能)的增加量
等于势能(或动能)的减少量.
(3)ΔEA=-ΔEB,即 A 物体机械能的增加量等于 B 物体机
械能的减少量.
2.解题步骤
(1)根据题意,先选取研究对象(物体或系统).
(2)明确研究对象的运动过程,分析对象在过程中的受力情
况及各力做功情况,判断是否满足机械能守恒的条件.
(3)选取恰当的表达式列方程求解.
机械能守恒定律 动能定理
应用范围 只有重力和弹力做功时 无条件限制
物理意义 其他力(重力、弹力以外)
所做的功是机械能变化的
量度 合外力对物体做的功是
动能变化的量度
关注角度 守恒的条件和始末状态机
械能的形式及大小 动能的变化及改变动能
方式(合外力做功情况)
说明 等号右边表示动能增加量
时,左边表示势能的减少
量,“mgh”表示重力势能
(或重力势能的变化) 等号左边是合外力的功,
右边是动能的增量,
“mgh”表示重力的功
3.机械能守恒定律和动能定理的比较
【例2】如图4-4-4所示,一固定的楔形木块,其斜面的
倾角为θ=30°,另一边与地面垂直,顶上有一个定滑轮,一根柔
软的不可伸长的细线跨过定滑轮,两端分别与物块 A 和 B 连接,
A 的质量为 4m,B 的质量为 m,开始时将 B 按在地面上不动,
然后放开手,让 A 沿斜面下滑而 B 上升,物块 A 与斜面间无摩
擦.求当 A 沿斜面下滑距离 s 时,A、B 的速度大小为多少?
图 4-4-4
解:因软绳不可伸长,可知A 下滑了s,B上升的距离也为
s,且A、B 的速度大小相等,设其速度为v,把A、B看做一个
系统.系统中仅有重力做功,机械能守恒.
方法一:假设地面为零势能面,未下滑时A 到斜面底端距
离为l,有
Ek1=0,Ep1=EpA1=4mglsin θ
当A 沿斜面下滑距离 s 时,有
2.如图 4-4-5 所示,质量为 m 的木块放在光滑的水平
桌面上,用轻绳绕过桌边定滑轮与质量为 M 的砝码相连,让绳
拉直后使砝码从静止开始下降 h(h 小于桌面的高度)的距离,木
块仍在桌面上,则砝码的速度大小为多少?
图 4-4-5
从能量转化观点解决机械能守恒问题
【例3】(双选)如图 4-4-6,质量分别为 m 和 2m 的两个
小球 A 和 B,中间用轻质杆相连,在杆的中点 O 处有一固定转
动轴,把杆置于水平位置后释放,在 B 球顺时针摆动到最低位
置的过程中(
)
图 4-4-6
A.B 球的重力势能减少,动能增加,B 球和地球组成的系
统机械能守恒
B.A 球的重力势能增加,动能也增加,A 球和地球组成的
系统机械能不守恒
C.A 球、B 球和地球组成的系统机械能守恒
D.A 球、B 球和地球组成的系统机械能不守恒
错因:认为杆施的力沿杆方向,拉力不做功,只有重力做
功,A、B 球的机械能都守恒.
正解:B 球从水平位置下摆到最低点过程中,受重力和杆
的作用力,杆的作用力方向待定.下摆过程中重力势能减少,
动能增加,但机械能是否守恒不确定.A 球在B 下摆过程中,
重力势能增加,动能增加,机械能增加.由于A、B系统只有
重力做功,系统机械能守恒,A 球机械能增加,B 球机械能一
定减少.所以B、C 选项正确.(杆施力的方向并不总指向沿杆
的方向,本题中就是如此.杆对A、B 球既有沿杆的法向力,
也有与杆垂直的切向力.所以杆对A、B球施的力都做功,A 球、
B 球的机械能都不守恒)
答案:BC
第四节 机械能守恒定律
一、动能与势能之间的相互转化
1.机械能:______与势能(包括__________和__________),
统称为机械能.
动能
重力势能
弹性势能
2.动能和势能的相互转化是通过______或______做功来实
现的.
重力
弹力
蹦极是非常刺激的户外休闲活动,深受年轻人的喜爱.跳
跃者站在约 40 米以上高度的桥梁、塔顶、高楼甚至热气球上.
人在蹦极时可在空中享受几秒钟的“自由落体”.当人体下落
到一定高度时,橡皮绳被拉开、绷紧,阻止人体
继续下落,当到达最低点时橡皮绳再次弹起,人
被拉起,随后,又落下,这样反复多次直到橡皮
绳的弹性消失为止,这就是蹦极的全过程.
你能简单说说人从最高处下落到最低点时
的能量转化过程吗?
图 4-4-1
答案:人从最高点下落到绳恰好伸直的过程:重力势能转
化为动能.从绳恰好伸直到绳的弹力 F=mg 的过程:重力势能
转化为动能和弹性势能.从绳的弹力 F=mg 到最低点的过程中:
重力势能和动能转化为弹性势能.整个过程可看成重力势能与
弹性势能间的相互转化.
二、机械能守恒定律
1.机械能守恒定律:在只有重力(或弹力)做功的情形下,
物体的动能和____________(或弹性势能)发生相互转化,而总
的机械能保持不变.
重力势能
Ek2+Ep2
2.表达式:Ek1+Ep1=__________或ΔEp+ΔEk=0.
要点1
机械能是否守恒的判断
1.从能量特点看:只有系统动能和势能相互转化,无其他
形式能量之间(如内能)转化,则系统机械能守恒.如果物体间
发生相互碰撞或相对运动,又有相互间的摩擦作用时有内能的
增加,机械能一般不守恒.
2.从机械能的定义看:若动能与势能之和不变化,则机械
能守恒.如果一个物体沿斜面匀速(或减速)滑下,动能不变(或
减小),势能减小,则机械能减小;一个物体沿水平方向匀速运
动时机械能守恒,沿竖直方向匀速运动时机械能不守恒.
3.从做功特点看:只有重力和系统内的弹力做功,系统机
械能守恒.具体表现在:
(1)只受重力(或系统内的弹力)作用.如:所有做抛体运动
的物体(不计阻力).
(2)还受其他力,但只有重力(或系统内的弹力)做功.如图
4-4-2 甲所示.
图 4-4-2
(3)有系统的内力做功,但是做功代数和为零.如图 4-4
-2 乙所示,A、B 间及 B 与地面之间均光滑,A 自 B 的上端自
由下滑时,B 沿地面滑动,A、B 之间的弹力做功,对 A 或 B 机
械能均不守恒,但对 A、B 组成的系统机械能守恒.
【例 1】(双选)如图 4-4-3 所示,下列关于机械能是否守
恒的判断正确的是(
)
图 4-4-3
A.甲图中,物体 A 将弹簧压缩的过程中,A 机械能守恒
B.乙图中,A 置于光滑水平面,物体 B 沿光滑斜面下滑,
物体 B 机械能守恒
C.丙图中,不计任何阻力时,A 加速下落,B 加速上升过
程中,A、B 组成的系统机械能守恒
D.丁图中,小球沿水平面做匀速圆锥摆运动时,小球的
机械能守恒
解析:甲图中,重力和弹力做功,物体 A 和弹簧组成的系
统机械能守恒,但物体 A 机械能不守恒,选项 A 错;乙图中,
物体 B 除受重力外,还受弹力,弹力对 B 做负功,机械能不守
恒,但从能量特点看,A、B 组成的系统机械能守恒,B 错;丙
图中,绳子张力对 A 做负功,对 B 做正功,代数和为零,A、
B 组成的系统机械能守恒,C 对;丁图中动能不变,势能不变,
机械能守恒,D 对.
答案:CD
1.(双选,2011 年东山中学期末)关于机械能是否守恒,下
列叙述中正确的是(
)
BD
A.做匀速直线运动的物体的机械能一定守恒
B.做匀变速运动的物体的机械能可能守恒
C.外力对物体做功为零时,机械能一定守恒
D.只有重力对物体做功,物体机械能一定守恒
要点2
机械能守恒定律的运用
1.机械能守恒定律的三种表达式
(1)Ek1+Ep1=Ek2+Ep2,即初状态的动能与势能之和等于末
状态的动能与势能之和,选用该表达式时,应恰当选取参考平面.
(2)ΔEk=-ΔEp 或ΔEp=-ΔEk,即动能(或势能)的增加量
等于势能(或动能)的减少量.
(3)ΔEA=-ΔEB,即 A 物体机械能的增加量等于 B 物体机
械能的减少量.
2.解题步骤
(1)根据题意,先选取研究对象(物体或系统).
(2)明确研究对象的运动过程,分析对象在过程中的受力情
况及各力做功情况,判断是否满足机械能守恒的条件.
(3)选取恰当的表达式列方程求解.
机械能守恒定律 动能定理
应用范围 只有重力和弹力做功时 无条件限制
物理意义 其他力(重力、弹力以外)
所做的功是机械能变化的
量度 合外力对物体做的功是
动能变化的量度
关注角度 守恒的条件和始末状态机
械能的形式及大小 动能的变化及改变动能
方式(合外力做功情况)
说明 等号右边表示动能增加量
时,左边表示势能的减少
量,“mgh”表示重力势能
(或重力势能的变化) 等号左边是合外力的功,
右边是动能的增量,
“mgh”表示重力的功
3.机械能守恒定律和动能定理的比较
【例2】如图4-4-4所示,一固定的楔形木块,其斜面的
倾角为θ=30°,另一边与地面垂直,顶上有一个定滑轮,一根柔
软的不可伸长的细线跨过定滑轮,两端分别与物块 A 和 B 连接,
A 的质量为 4m,B 的质量为 m,开始时将 B 按在地面上不动,
然后放开手,让 A 沿斜面下滑而 B 上升,物块 A 与斜面间无摩
擦.求当 A 沿斜面下滑距离 s 时,A、B 的速度大小为多少?
图 4-4-4
解:因软绳不可伸长,可知A 下滑了s,B上升的距离也为
s,且A、B 的速度大小相等,设其速度为v,把A、B看做一个
系统.系统中仅有重力做功,机械能守恒.
方法一:假设地面为零势能面,未下滑时A 到斜面底端距
离为l,有
Ek1=0,Ep1=EpA1=4mglsin θ
当A 沿斜面下滑距离 s 时,有
2.如图 4-4-5 所示,质量为 m 的木块放在光滑的水平
桌面上,用轻绳绕过桌边定滑轮与质量为 M 的砝码相连,让绳
拉直后使砝码从静止开始下降 h(h 小于桌面的高度)的距离,木
块仍在桌面上,则砝码的速度大小为多少?
图 4-4-5
从能量转化观点解决机械能守恒问题
【例3】(双选)如图 4-4-6,质量分别为 m 和 2m 的两个
小球 A 和 B,中间用轻质杆相连,在杆的中点 O 处有一固定转
动轴,把杆置于水平位置后释放,在 B 球顺时针摆动到最低位
置的过程中(
)
图 4-4-6
A.B 球的重力势能减少,动能增加,B 球和地球组成的系
统机械能守恒
B.A 球的重力势能增加,动能也增加,A 球和地球组成的
系统机械能不守恒
C.A 球、B 球和地球组成的系统机械能守恒
D.A 球、B 球和地球组成的系统机械能不守恒
错因:认为杆施的力沿杆方向,拉力不做功,只有重力做
功,A、B 球的机械能都守恒.
正解:B 球从水平位置下摆到最低点过程中,受重力和杆
的作用力,杆的作用力方向待定.下摆过程中重力势能减少,
动能增加,但机械能是否守恒不确定.A 球在B 下摆过程中,
重力势能增加,动能增加,机械能增加.由于A、B系统只有
重力做功,系统机械能守恒,A 球机械能增加,B 球机械能一
定减少.所以B、C 选项正确.(杆施力的方向并不总指向沿杆
的方向,本题中就是如此.杆对A、B 球既有沿杆的法向力,
也有与杆垂直的切向力.所以杆对A、B球施的力都做功,A 球、
B 球的机械能都不守恒)
答案:BC
同课章节目录
- 第一章 抛体运动
- 第01节 什么是抛体运动
- 第02节 运动的合成与分解
- 第03节 竖直方向的抛体运动
- 第04节 平抛运动
- 第05节 斜抛运动
- 第二章 圆周运动
- 第01节 匀速圆周运动
- 第02节 向心力
- 第03节 离心现象及其应用
- 第三章 万有引力定律及其应用
- 第01节 万有引力定律
- 第02节 万有引力定律的应用
- 第03节 飞向太空
- 第四章 机械能和能源
- 第01节 功
- 第02节 动能 势能
- 第03节 探究外力做功与物体动能变化的关系
- 第04节 机械能守恒定律
- 第05节 验证机械能守恒定律
- 第06节 能量 能量转化与守恒定律
- 第07节 功率
- 第08节 能源的开发与利用
- 第五章 经典力学与物理学的革命
- 第01节 经典力学的成就与局限性
- 第02节 经典时空观与相对论时空观
- 第03节 量子化现象
- 第04节 物理学——人类文明进步的阶梯
