苏科版八年级数学上册 3.1 勾股定理(课件)(共18张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 3.1 勾股定理(课件)(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-25 08:32:03 | ||
图片预览


文档简介
(共18张PPT)
3.1 勾股定理
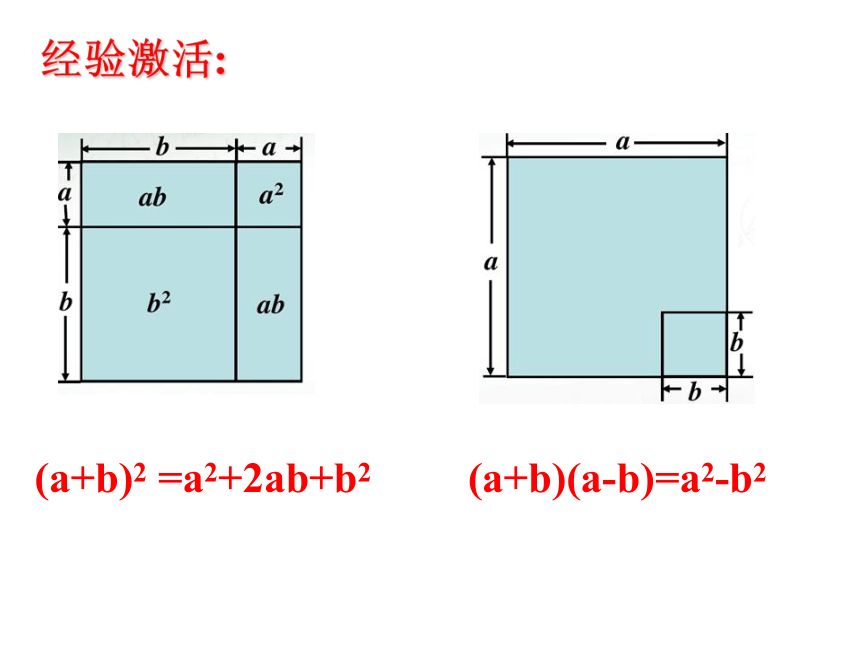
(a+b)2 =a2+2ab+b2
(a+b)(a-b)=a2-b2
经验激活:
a
b
c
d
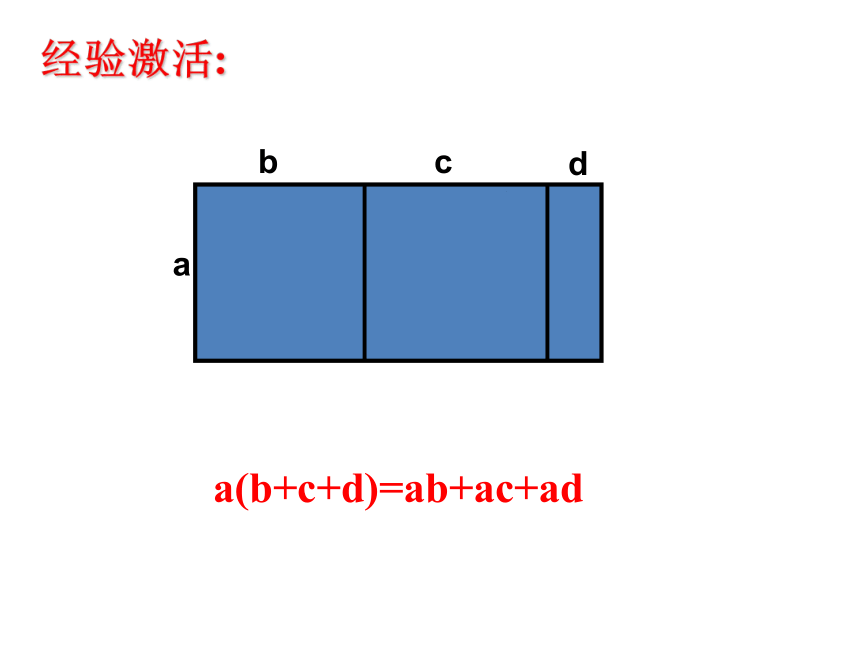
a(b+c+d)=ab+ac+ad
经验激活:
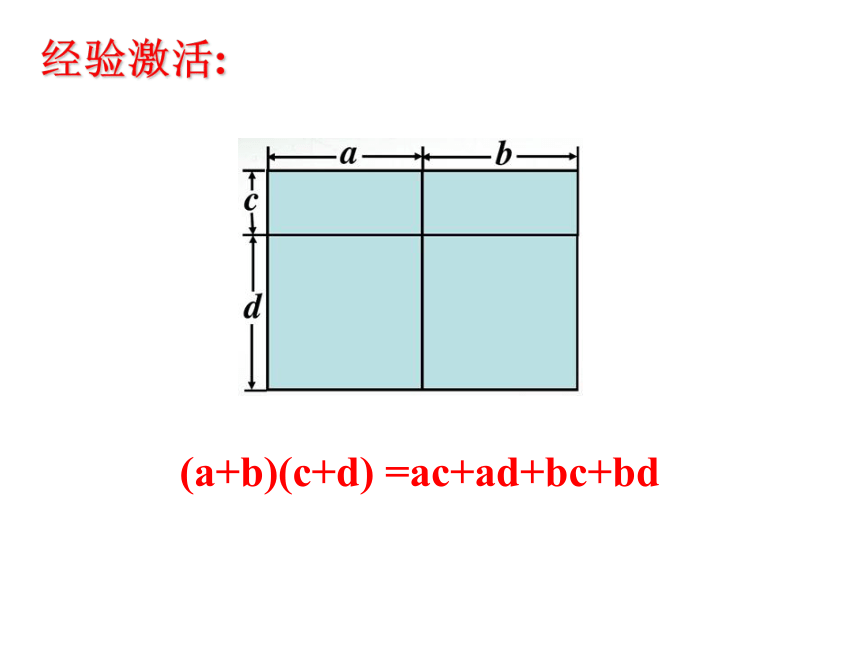
(a+b)(c+d) =ac+ad+bc+bd
经验激活:
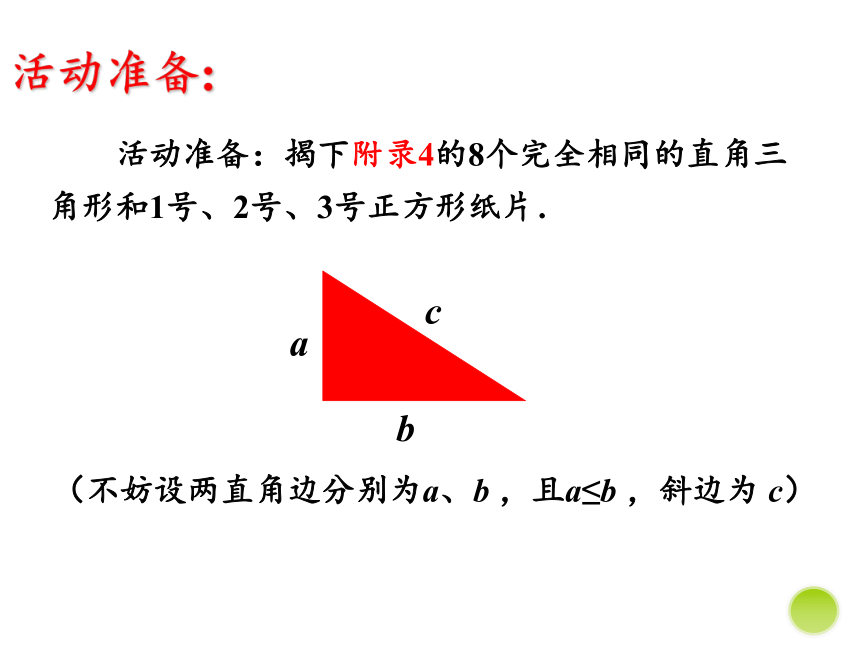
活动准备:
活动准备:揭下附录4的8个完全相同的直角三角形和1号、2号、3号正方形纸片.
a
b
c
(不妨设两直角边分别为a、b ,且a≤b ,斜边为 c)
活动一:图形验证勾股定理
(1)选用4个完全相同的直角三角形和1号正方形纸片,拼成1个新的正方形;
(2)选用4个完全相同的直角三角形和2号、3号正方形纸片,拼成1个新的正方形;
(3)你能利用所拼成的2个正方形证明验证勾股定理吗?
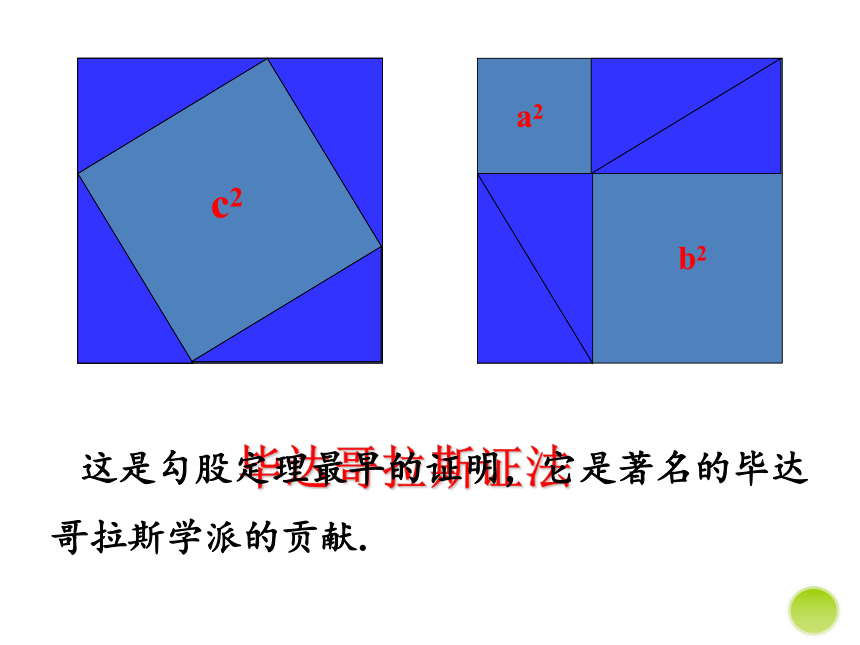
毕达哥拉斯证法
这是勾股定理最早的证明,它是著名的毕达哥拉斯学派的贡献.
c2
a2
b2
毕达哥拉斯证法
这种证法不仅最早,而且也是最直观的图形验证的方法,它可以不用图形之外的语言让我们看明白勾股定理的正确性.
a
a
a
a
b
b
b
b
c
c
c
c
活动二:你能只利用这一个图形验证勾股定理吗?
邹元治证法
你还能只利用4个完全相同的直角三角形拼成边长为c的正方形验证勾股定理吗?
a
b
c
(不妨设两直角边分别为a、b ,且a≤b ,斜边为 c)
赵爽弦图
这个图案是我国古代著名的数学家赵爽在注解《周髀算经》时所给出.
这也是我国对于勾股定理的第一个证明,代表了我国古代数学的成就.
总统证法
活动三:你能只利用2个完全相同的直角三角形所拼成的图形验证勾股定理吗?
美国第20届总统:
伽菲尔德
a2
b2
活动四:如何把两个正方形纸片通过裁剪拼成一个正方形?
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的"面积法"给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1摆放时,都可以用"面积法"来证明,请你帮助小聪.
求证:a2+b2=c2
课堂练习:
图1
课堂小结:
谈谈通过本节课的学习,你有哪些收获和感悟?
课堂练习
数缺形时少直观,
形缺数时难入微.
数形结合百般好,
隔离分家万事休.
——华罗庚
名人名言:
谢 谢
3.1 勾股定理
(a+b)2 =a2+2ab+b2
(a+b)(a-b)=a2-b2
经验激活:
a
b
c
d
a(b+c+d)=ab+ac+ad
经验激活:
(a+b)(c+d) =ac+ad+bc+bd
经验激活:
活动准备:
活动准备:揭下附录4的8个完全相同的直角三角形和1号、2号、3号正方形纸片.
a
b
c
(不妨设两直角边分别为a、b ,且a≤b ,斜边为 c)
活动一:图形验证勾股定理
(1)选用4个完全相同的直角三角形和1号正方形纸片,拼成1个新的正方形;
(2)选用4个完全相同的直角三角形和2号、3号正方形纸片,拼成1个新的正方形;
(3)你能利用所拼成的2个正方形证明验证勾股定理吗?
毕达哥拉斯证法
这是勾股定理最早的证明,它是著名的毕达哥拉斯学派的贡献.
c2
a2
b2
毕达哥拉斯证法
这种证法不仅最早,而且也是最直观的图形验证的方法,它可以不用图形之外的语言让我们看明白勾股定理的正确性.
a
a
a
a
b
b
b
b
c
c
c
c
活动二:你能只利用这一个图形验证勾股定理吗?
邹元治证法
你还能只利用4个完全相同的直角三角形拼成边长为c的正方形验证勾股定理吗?
a
b
c
(不妨设两直角边分别为a、b ,且a≤b ,斜边为 c)
赵爽弦图
这个图案是我国古代著名的数学家赵爽在注解《周髀算经》时所给出.
这也是我国对于勾股定理的第一个证明,代表了我国古代数学的成就.
总统证法
活动三:你能只利用2个完全相同的直角三角形所拼成的图形验证勾股定理吗?
美国第20届总统:
伽菲尔德
a2
b2
活动四:如何把两个正方形纸片通过裁剪拼成一个正方形?
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的"面积法"给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1摆放时,都可以用"面积法"来证明,请你帮助小聪.
求证:a2+b2=c2
课堂练习:
图1
课堂小结:
谈谈通过本节课的学习,你有哪些收获和感悟?
课堂练习
数缺形时少直观,
形缺数时难入微.
数形结合百般好,
隔离分家万事休.
——华罗庚
名人名言:
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
