苏科版2021-2022学年八年级上学期数学第一章全等三角形考点训练(word解析版)
文档属性
| 名称 | 苏科版2021-2022学年八年级上学期数学第一章全等三角形考点训练(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-25 09:07:05 | ||
图片预览




文档简介
第一章全等三角形考点训练
考点一、网格中的全等三角形
如图为正方形网格,则
A. B. C. D.
如图,正方形网格中的网格线交点称为格点.的三个顶点为三个格点,如果P是图中异于C点的格点,且以A,B,P为顶点的三角形与全等,则符合条件的P点有
A. 1个 B. 2个 C. 3个 D. 4个
如图,在3x3的正方形网格中,度.
A. B. C. D.
如图是一个的正方形网格,图中所标示的7个角的角度之和等于
A. B. C. D.
如图,是由4个相同的小正方形组成的网格图,其中等于
A. B. C. D.
如图,方格中的三个顶点分别在小正方形的顶点格点上,这样的三角形叫做格点三角形,图中可以画出与全等的格点三角形不含共有
21个 B. 22个 C. 23个 D. 2
考点二、全等三角形判定的应用
公路上,A,B两站相距25千米,C、D为两所学校,于点A,于点B,如图,已知千米,现在要在公路AB上建一报亭H,使得C、D两所学校到H的距离相等,且,问:H应建在距离A站多远处?学校C到公路的距离是多少千米?
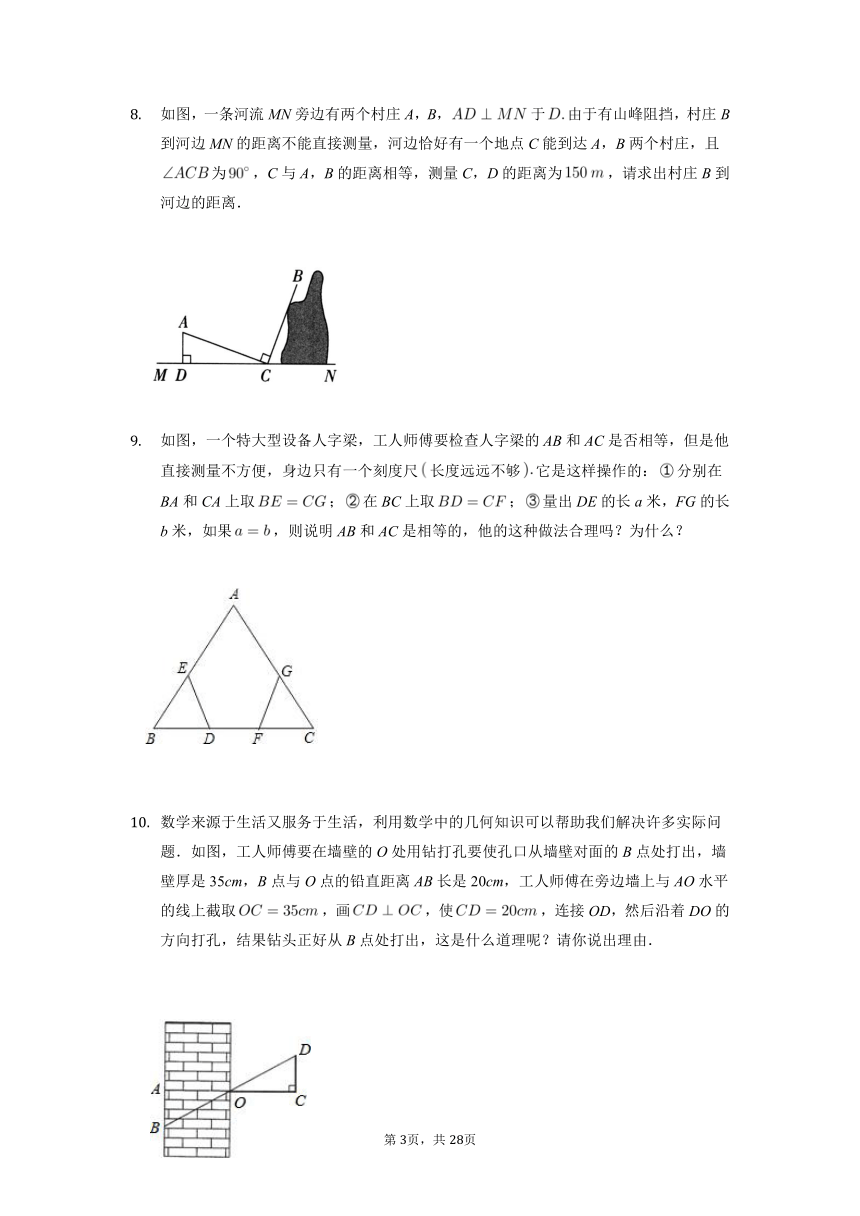
如图,一条河流MN旁边有两个村庄A,B,于由于有山峰阻挡,村庄B到河边MN的距离不能直接测量,河边恰好有一个地点C能到达A,B两个村庄,且为,C与A,B的距离相等,测量C,D的距离为,请求出村庄B到河边的距离.
如图,一个特大型设备人字梁,工人师傅要检查人字梁的AB和AC是否相等,但是他直接测量不方便,身边只有一个刻度尺长度远远不够它是这样操作的:分别在BA和CA上取;在BC上取;量出DE的长a米,FG的长b米,如果,则说明AB和AC是相等的,他的这种做法合理吗?为什么?
数学来源于生活又服务于生活,利用数学中的几何知识可以帮助我们解决许多实际问题.如图,工人师傅要在墙壁的O处用钻打孔要使孔口从墙壁对面的B点处打出,墙壁厚是35cm,B点与O点的铅直距离AB长是20cm,工人师傅在旁边墙上与AO水平的线上截取,画,使,连接OD,然后沿着DO的方向打孔,结果钻头正好从B点处打出,这是什么道理呢?请你说出理由.
某段河流的两岸是平行的,数学兴趣小组的同学们计划不用涉水过河测量河的宽度.他们是这样做的:
在河流的一条岸边B点,选对岸正对的一棵树A;
沿河岸直走8m到达树C,继续前行8m到达D处;
从D处沿河岸垂直的方向行走,当到达树A正好被树C遮挡住的E处停止行走;
测得DE的长为5m.
请你继续解决问题:
河的宽度是______m;
证明他们做法的正确性.
如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:
在岸边确定一点C,使C与A,B在同一直线上;
在AC的垂直方向画线段CD,取其中点O;
画使F、O、A在同一直线上;
在线段DF上找一点E,使E与O、B共线.
他说测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
考点三、全等三角形的性质与判定
如图,,,,.
求的度数;
若,求证:.
如图所示,在四边形ABCD中,,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
判断FC与AD的数量关系,并说明理由;
若,则吗?为什么?
如图,在和中,,,AC与DB交于点M.
求证:≌;
过点C作,过点B作,CN与BN交于点N,试判断的形状,并证明你的结论.
如图,在中,,DE是过点A的直线,于点D,于点E,.
若BC在DE的同侧如图求证:.
若BC在DE的两侧如图,其他条件不变,中的结论还成立吗?不需证明
如图,在线段BC上有两点E,F,在线段CB的异侧有两点A,D,满足,,,连接AF;
求证:;
若,,当AF平分时,求.
考点四、全等三角形的动点问题
如图,,,,,垂足分别为D,E.
证明:≌;
若,,求DE的长.
如图,,,,点P在线段AB上以的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t秒.
若点Q的运动速度与点P的运动速度相等,当时,与是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
如图,将图中的“,”改为“”,其他条件不变.设点Q的运动速度为,是否存在实数x,使得与全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
在中,,D为射线BC上的一动点不与点B、C重合,在AD的右侧作,使,,连接CE.
点D在线段BC上时
求证:≌;
当点D从点B开始运动时,的度数等于_________用含的式子表示;
当点D运动到线段BC上何处时,,并说明理由;
当时,若,,请直接写出的值为______________
已知等腰直角,,点D是斜边AB的中点,E是AC上的动点、,DF交BC于点F.
当,时,如图,我们很容易得出:
如图2,DE与AC不垂直,且点E在线段AC上时,中的结论是否成立,如果不成立,请说明理由;如果成立,请证明.
当点E运动到AC延长线上,其他条件不变,请把图3补充完整,直接写出,,的关系.
如图1,在中,,,分别过B、C两点作过点A的直线m的垂线,垂足为D、E;
如图1,当D、E两点在直线BC的同侧时,猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由.
如图,将中的条件改为:在中,,D、A、E三点都在直线m上,并且有,其中为任意锐角或钝角.请问的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
如图3,,,点P从B点出发沿路径向终点C运动;点Q从C点出发沿路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时,该点停止运动,另一点继续运动到终点为止;在运动过程中,分别过P和Q作于F,于问:点P运动多少秒时,与全等?直接写出结果即可
如图,中,D为AB的中点,厘米,,厘米.
若点P在线段BC上以3厘米秒的速度从点B向终点C运动,同时点Q在线段CA上从点C向终点A运动,
若点Q的速度与点P的速度相等,经1秒钟后,请说明≌;
点Q的速度与点P的速度不相等,当点Q的速度为多少时,能够使≌;
若点P以3厘米秒的速度从点B向点C运动,同时点Q以5厘米秒的速度从点C向点A运动,它们都依次沿三边运动,则经过多长时间,点Q第一次在的哪条边上追上点P?
答案和解析
1.【答案】B
【解析】
【分析】
本题考查了正方形的性质和全等三角形的判定,充分利用正方形的特殊性质来找到全等的条件从而判定全等后利用全等三角形的性质解题根据对称性可得,,从而可得答案.
【解答】
解:在和中
,
≌,
所在的三角形与所在的三角形全等,
,
又,
.
故选B.
2.【答案】C
【解析】
【分析】
本题考查了对全等三角形的判定定理的应用,熟练掌握全等三角形的判定定理是解题关键.
根据三角形的各种判定方法借助于网格即可求出符合题意的点P.
【解答】
解:如图所示:
故选C.
3.【答案】D
【解析】
【分析】
本题考查全等图形,解答本题的关键是明确题意,作出合适的辅助线,利用数形结合的思想解答.根据全等三角形的判定和性质即可得到结论.
【解答】
解:如图所示,
,,,
≌,
,
,
,
故选D.
4.【答案】A
【解析】解:仔细观察图形,我们可以发现:
,,,
≌,
,
同理可得:
,
,
,
所以说图示的7个角的度数和为.
该题考查学生的观察能力,由此图可以看出左边第一个角和下面第一个角之和为.
本题考查了全等三角形对应角相等的性质,求证全等三角形,找出对应角是解决本题的关键.
5.【答案】B
【解析】
【试题解析】
【分析】
本题考查全等三角形的知识,解答本题的关键是证明根据SAS可证得,可得出,继而可得出答案.
【解答】
解:
由题意得:,,,
,
,即.
,
.
故选B.
6.【答案】C
【解析】解:用SSS判定两三角形全等,所以共有24个全等三角形,
除去外有23个与全等的三角形.
故选:C.
用SSS判定两三角形全等.认真观察图形可得答案.
此题主要考查了全等三角形的判定以及格点三角形的定义,利用数形结合与分类讨论是解决问题的关键.
7.【答案】解:,
,
,
,
,
在和中,,
≌,
千米,,
,B两站相距25千米,
千米,
千米,
学校C到公路的距离是10千米.
答:H应建在距离A站10千米处,学校C到公路的距离是10千米.
【解析】根据同角的余角相等求出,再利用“角角边”证明和全等,根据全等三角形对应边相等可得,,再根据计算即可得解.
本题考查了全等三角形的应用,全等三角形的性质,熟练掌握全等三角形的判定方法求出两三角形全等是解题的关键.
8.【答案】解:如图,过点B作于点E,
,
,,
在与中,
≌.
,
即村庄B到河边的距离是.
【解析】见答案.
9.【答案】解:合理,理由:
在和中,
,
≌,
,
.
【解析】利用全等三角形的判定方法得出≌,进而得出答案.
此题主要考查了全等三角形的应用,根据题意正确得出对应边相等是解题关键.
10.【答案】解:理由:
,墙壁厚,
,
墙体是垂直的, 且,
,
在和中,
,
≌,
,
,
,
钻头正好从B点出打出.
【解析】由≌,推出即可解决问题;
本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
11.【答案】5
【解析】证明:由题意知,米,即河的宽度是5米.
故答案是:5.
如图,由题意知,在和中,
,
≌,
.
即他们的做法是正确的.
将题目中的实际问题转化为数学问题,然后利用全等三角形的判定方法证得两个三角形全等即可说明其做法的正确性.
本题考查了全等三角形的应用,解题的关键是将实际问题转化为数学问题.
12.【答案】解:有道理,
,,
,
为CD中点,
,
在和中,
≌,
,,
在和中,
≌,
.
【解析】首先证明≌,根据全等三角形的性质可得,,再证明≌,进而可得.
此题主要全等三角形的应用,关键是掌握全等三角形的判定方法和性质定理.
13.【答案】解,,
,
,
;
证明:;,
,
在与中,
,
≌,
.
【解析】本题考查全等三角形的性质和判定,平行线的性质,
根据平行线的性质可得,再根据角的和差关系即可求解;
根据ASA可证≌,再根据全等三角形的性质即可求解.
14.【答案】解:结论:.
理由:,
,
是CD的中点,
,
在与中,
,
≌,
;
结论:.
理由:由知≌,
,,
,
,
即,
≌,
,
;
【解析】结论:只要证明≌即可;
想办法证明,理由等腰三角形的性质即可解决问题;
本题考查全等三角形的判定和性质、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
15.【答案】证明:如图,在和中,
,
≌;
解:是等腰三角形.证明如下:
,,
四边形BMCN是平行四边形,
由知,,
等角对等边,
四边形BMCN是菱形,
.
【解析】由SSS可证≌;
是等腰三角形,可先证明四边形BMCN是平行四边形,由知,,可得,于是就有四边形BMCN是菱形,则.
本题考查了全等三角形的判定与性质,难度一般,对于此类题目要注意掌握三角形全等及菱形判定定理.
16.【答案】证明:于点D,于点E,
和均为直角三角形.
在和中,,
≌,
.
又,
,
,
.
解:,理由如下:
同可证出:≌,
.
又,
,
.
【解析】由于点D、于点E,可得出和均为直角三角形,由、即可证出≌,根据全等三角形的性质可得出,结合可得出,再利用角的计算可求出,即;
同可得出,结合可得出,即.
本题考查了全等三角形的判定与性质以及角的计算,解题的关键是:利用全等三角形的性质结合角的计算找出;利用全等三角形的性质结合角的计算找出.
17.【答案】解:,
,
,
在和中,
≌,
;
解:由得:≌,
,
,
平分,
.
【解析】此题考查全等三角形的判定和性质、角平分线的定义、三角形内角和定理,熟练掌握全等三角形的判定和性质定理是解题关键.
首先根据,通过,证得,然后根据全等三角形的判定定理证得≌,最后根据全等三角形的性质即可证得;
首先根据全等三角形的性质证得,然后根据三角形的内角和定理求出的度数,最后根据角平分线的定义即可求出的度数.
18.【答案】解:,,,
,
,,
,
在和中,
≌;
≌,
,,
.
【解析】本题考查了全等三角形的性质和判定,垂线的定义等知识点的应用,解此题的关键是推出证明和全等的三个条件.
根据垂直定义求出,根据等式性质求出,根据AAS证明≌;
根据全等三角形的对应边相等得到,,利用,即可解答.
19.【答案】解:当时,,,
又,
在和中,
≌.
,
.
,
故线段PC与线段PQ垂直.
若≌,
则,,
,
解得;
若≌,
则,,
,
解得;
故存在或使得与全等.
【解析】此题考查全等三角形的判定与性质,注意分类讨论思想的渗透.
利用SAS证得≌,得出,进一步得出得出结论即可;
由≌,分两种情况:,,,,建立方程组求得答案即可.
20.【答案】证明:
,
即,
在和中,
,,
≌ .
解:由题意可得:.
解:当点D运动到线段BC的中点时,,
点D是线段BC的中点,
,
,
,
.
或20.
【解析】
【分析】
本题考查的是全等三角形的判定与性质,
根据题意找出三角形全等的条件即可解答;
根据题意直接进行解答即可;
当点D运动到线段BC的中点时,,然后再进行解答即可.
根据题意直接进行解答即可.
【解答】
见答案;
解:由题意可得:或28.
故答案为68或20.
21.【答案】解:,,
,,
点D是斜边AB的中点,,
,
,
;
答:结论仍然成立,
证明:如图2,过D作于M,于N,
,
,,
点D是斜边AB的中点,
,,
,
四边形CNDM是正方形,
,
,
,
在与中,,
≌,,
;
如图3,
过D作于M,于N,
,
,,
点D是斜边AB的中点,
,,
,
四边形CNDM是正方形,
,
,
,
在与中,,
≌,,
.
【解析】根据三角形的中位线和正方形的性质即可得到结论;
如图2,过D作于M,于N,根据三角形的中位线大小在得到,推出四边形CNDM是正方形,得到,根据余角的性质得到,根据全等三角形的性质得到≌,于是得到结论;
如图3,过D作于M,于N,根据三角形的中位线大小在得到,推出四边形CNDM是正方形,得到,根据余角的性质得到,根据全等三角形的性质得到≌,于是得到结论.
本题考查了等腰直角三角形的性质,全等三角形的判定和性质,正方形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.
22.【答案】证明:直线m,直线m,
,
,
,
,
,
在和中,
,
≌,
,,
;
,
,
,
在和中,
,
≌,
,,
.
当t等于6、10或22时,与全等.
【解析】
【分析】
本题考查了全等三角形的判定与性质以及分类讨论的思想,可能会因考虑不全面而出错,是一道易错题.判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;得出是解题关键.
根据直线m,直线m得,而,根据等角的余角相等得,然后根据“AAS”可判断≌,则,,于是;
利用,则,得出,进而得出≌即可得出答案;
易证,,只需,就可得到与全等,然后只需根据点P和点Q不同位置进行分类讨论即可解决问题.
【解答】
解:见答案;
见答案;
当时,点P在AB上,点Q在AC上,
此时有,,,.
当即,也即时,
,,,
.
.
在和中,
,
与≌.
当时,点P在AB上,点Q也在AB上,
此时相当于两点相遇,则有,解得;
当时,点Q在点AB上,点P在AC上,当即,解得舍去;
当时,点Q停在点B的位置,点P在AC上,当即,解得,
综上所述:当t等于6、10或22时,与全等.
23.【答案】解:,
,
,,
,
为AB的中点,
,
,
,
在与中,
,
≌;
设点Q运动时间为t秒,运动速度为,
≌CPQ,
,,
,
;
设经过x秒后,点Q第一次追上点P,由题意得,
解得:,
点P运动的路程为,
,
此时点P在BC边上,
经过10秒,点Q第一次在BC边上追上点P.
【解析】本题考查了全等三角形的判定和性质,找准对应边是解题的关键.
根据等腰三角形的性质得到,再加上,,则可判断与全等;
设点Q的运动速度为,则,,,当≌,则,;然后分别建立关于t和v的方程,再解方程即可;
设经过x秒后,点Q第一次追上点P,由题意得,解方程得到点P运动的路程为,得到此时点P在BC边上,于是得到结果.
第2页,共2页
第1页,共1页
考点一、网格中的全等三角形
如图为正方形网格,则
A. B. C. D.
如图,正方形网格中的网格线交点称为格点.的三个顶点为三个格点,如果P是图中异于C点的格点,且以A,B,P为顶点的三角形与全等,则符合条件的P点有
A. 1个 B. 2个 C. 3个 D. 4个
如图,在3x3的正方形网格中,度.
A. B. C. D.
如图是一个的正方形网格,图中所标示的7个角的角度之和等于
A. B. C. D.
如图,是由4个相同的小正方形组成的网格图,其中等于
A. B. C. D.
如图,方格中的三个顶点分别在小正方形的顶点格点上,这样的三角形叫做格点三角形,图中可以画出与全等的格点三角形不含共有
21个 B. 22个 C. 23个 D. 2
考点二、全等三角形判定的应用
公路上,A,B两站相距25千米,C、D为两所学校,于点A,于点B,如图,已知千米,现在要在公路AB上建一报亭H,使得C、D两所学校到H的距离相等,且,问:H应建在距离A站多远处?学校C到公路的距离是多少千米?
如图,一条河流MN旁边有两个村庄A,B,于由于有山峰阻挡,村庄B到河边MN的距离不能直接测量,河边恰好有一个地点C能到达A,B两个村庄,且为,C与A,B的距离相等,测量C,D的距离为,请求出村庄B到河边的距离.
如图,一个特大型设备人字梁,工人师傅要检查人字梁的AB和AC是否相等,但是他直接测量不方便,身边只有一个刻度尺长度远远不够它是这样操作的:分别在BA和CA上取;在BC上取;量出DE的长a米,FG的长b米,如果,则说明AB和AC是相等的,他的这种做法合理吗?为什么?
数学来源于生活又服务于生活,利用数学中的几何知识可以帮助我们解决许多实际问题.如图,工人师傅要在墙壁的O处用钻打孔要使孔口从墙壁对面的B点处打出,墙壁厚是35cm,B点与O点的铅直距离AB长是20cm,工人师傅在旁边墙上与AO水平的线上截取,画,使,连接OD,然后沿着DO的方向打孔,结果钻头正好从B点处打出,这是什么道理呢?请你说出理由.
某段河流的两岸是平行的,数学兴趣小组的同学们计划不用涉水过河测量河的宽度.他们是这样做的:
在河流的一条岸边B点,选对岸正对的一棵树A;
沿河岸直走8m到达树C,继续前行8m到达D处;
从D处沿河岸垂直的方向行走,当到达树A正好被树C遮挡住的E处停止行走;
测得DE的长为5m.
请你继续解决问题:
河的宽度是______m;
证明他们做法的正确性.
如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:
在岸边确定一点C,使C与A,B在同一直线上;
在AC的垂直方向画线段CD,取其中点O;
画使F、O、A在同一直线上;
在线段DF上找一点E,使E与O、B共线.
他说测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
考点三、全等三角形的性质与判定
如图,,,,.
求的度数;
若,求证:.
如图所示,在四边形ABCD中,,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
判断FC与AD的数量关系,并说明理由;
若,则吗?为什么?
如图,在和中,,,AC与DB交于点M.
求证:≌;
过点C作,过点B作,CN与BN交于点N,试判断的形状,并证明你的结论.
如图,在中,,DE是过点A的直线,于点D,于点E,.
若BC在DE的同侧如图求证:.
若BC在DE的两侧如图,其他条件不变,中的结论还成立吗?不需证明
如图,在线段BC上有两点E,F,在线段CB的异侧有两点A,D,满足,,,连接AF;
求证:;
若,,当AF平分时,求.
考点四、全等三角形的动点问题
如图,,,,,垂足分别为D,E.
证明:≌;
若,,求DE的长.
如图,,,,点P在线段AB上以的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t秒.
若点Q的运动速度与点P的运动速度相等,当时,与是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
如图,将图中的“,”改为“”,其他条件不变.设点Q的运动速度为,是否存在实数x,使得与全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
在中,,D为射线BC上的一动点不与点B、C重合,在AD的右侧作,使,,连接CE.
点D在线段BC上时
求证:≌;
当点D从点B开始运动时,的度数等于_________用含的式子表示;
当点D运动到线段BC上何处时,,并说明理由;
当时,若,,请直接写出的值为______________
已知等腰直角,,点D是斜边AB的中点,E是AC上的动点、,DF交BC于点F.
当,时,如图,我们很容易得出:
如图2,DE与AC不垂直,且点E在线段AC上时,中的结论是否成立,如果不成立,请说明理由;如果成立,请证明.
当点E运动到AC延长线上,其他条件不变,请把图3补充完整,直接写出,,的关系.
如图1,在中,,,分别过B、C两点作过点A的直线m的垂线,垂足为D、E;
如图1,当D、E两点在直线BC的同侧时,猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由.
如图,将中的条件改为:在中,,D、A、E三点都在直线m上,并且有,其中为任意锐角或钝角.请问的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
如图3,,,点P从B点出发沿路径向终点C运动;点Q从C点出发沿路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时,该点停止运动,另一点继续运动到终点为止;在运动过程中,分别过P和Q作于F,于问:点P运动多少秒时,与全等?直接写出结果即可
如图,中,D为AB的中点,厘米,,厘米.
若点P在线段BC上以3厘米秒的速度从点B向终点C运动,同时点Q在线段CA上从点C向终点A运动,
若点Q的速度与点P的速度相等,经1秒钟后,请说明≌;
点Q的速度与点P的速度不相等,当点Q的速度为多少时,能够使≌;
若点P以3厘米秒的速度从点B向点C运动,同时点Q以5厘米秒的速度从点C向点A运动,它们都依次沿三边运动,则经过多长时间,点Q第一次在的哪条边上追上点P?
答案和解析
1.【答案】B
【解析】
【分析】
本题考查了正方形的性质和全等三角形的判定,充分利用正方形的特殊性质来找到全等的条件从而判定全等后利用全等三角形的性质解题根据对称性可得,,从而可得答案.
【解答】
解:在和中
,
≌,
所在的三角形与所在的三角形全等,
,
又,
.
故选B.
2.【答案】C
【解析】
【分析】
本题考查了对全等三角形的判定定理的应用,熟练掌握全等三角形的判定定理是解题关键.
根据三角形的各种判定方法借助于网格即可求出符合题意的点P.
【解答】
解:如图所示:
故选C.
3.【答案】D
【解析】
【分析】
本题考查全等图形,解答本题的关键是明确题意,作出合适的辅助线,利用数形结合的思想解答.根据全等三角形的判定和性质即可得到结论.
【解答】
解:如图所示,
,,,
≌,
,
,
,
故选D.
4.【答案】A
【解析】解:仔细观察图形,我们可以发现:
,,,
≌,
,
同理可得:
,
,
,
所以说图示的7个角的度数和为.
该题考查学生的观察能力,由此图可以看出左边第一个角和下面第一个角之和为.
本题考查了全等三角形对应角相等的性质,求证全等三角形,找出对应角是解决本题的关键.
5.【答案】B
【解析】
【试题解析】
【分析】
本题考查全等三角形的知识,解答本题的关键是证明根据SAS可证得,可得出,继而可得出答案.
【解答】
解:
由题意得:,,,
,
,即.
,
.
故选B.
6.【答案】C
【解析】解:用SSS判定两三角形全等,所以共有24个全等三角形,
除去外有23个与全等的三角形.
故选:C.
用SSS判定两三角形全等.认真观察图形可得答案.
此题主要考查了全等三角形的判定以及格点三角形的定义,利用数形结合与分类讨论是解决问题的关键.
7.【答案】解:,
,
,
,
,
在和中,,
≌,
千米,,
,B两站相距25千米,
千米,
千米,
学校C到公路的距离是10千米.
答:H应建在距离A站10千米处,学校C到公路的距离是10千米.
【解析】根据同角的余角相等求出,再利用“角角边”证明和全等,根据全等三角形对应边相等可得,,再根据计算即可得解.
本题考查了全等三角形的应用,全等三角形的性质,熟练掌握全等三角形的判定方法求出两三角形全等是解题的关键.
8.【答案】解:如图,过点B作于点E,
,
,,
在与中,
≌.
,
即村庄B到河边的距离是.
【解析】见答案.
9.【答案】解:合理,理由:
在和中,
,
≌,
,
.
【解析】利用全等三角形的判定方法得出≌,进而得出答案.
此题主要考查了全等三角形的应用,根据题意正确得出对应边相等是解题关键.
10.【答案】解:理由:
,墙壁厚,
,
墙体是垂直的, 且,
,
在和中,
,
≌,
,
,
,
钻头正好从B点出打出.
【解析】由≌,推出即可解决问题;
本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
11.【答案】5
【解析】证明:由题意知,米,即河的宽度是5米.
故答案是:5.
如图,由题意知,在和中,
,
≌,
.
即他们的做法是正确的.
将题目中的实际问题转化为数学问题,然后利用全等三角形的判定方法证得两个三角形全等即可说明其做法的正确性.
本题考查了全等三角形的应用,解题的关键是将实际问题转化为数学问题.
12.【答案】解:有道理,
,,
,
为CD中点,
,
在和中,
≌,
,,
在和中,
≌,
.
【解析】首先证明≌,根据全等三角形的性质可得,,再证明≌,进而可得.
此题主要全等三角形的应用,关键是掌握全等三角形的判定方法和性质定理.
13.【答案】解,,
,
,
;
证明:;,
,
在与中,
,
≌,
.
【解析】本题考查全等三角形的性质和判定,平行线的性质,
根据平行线的性质可得,再根据角的和差关系即可求解;
根据ASA可证≌,再根据全等三角形的性质即可求解.
14.【答案】解:结论:.
理由:,
,
是CD的中点,
,
在与中,
,
≌,
;
结论:.
理由:由知≌,
,,
,
,
即,
≌,
,
;
【解析】结论:只要证明≌即可;
想办法证明,理由等腰三角形的性质即可解决问题;
本题考查全等三角形的判定和性质、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
15.【答案】证明:如图,在和中,
,
≌;
解:是等腰三角形.证明如下:
,,
四边形BMCN是平行四边形,
由知,,
等角对等边,
四边形BMCN是菱形,
.
【解析】由SSS可证≌;
是等腰三角形,可先证明四边形BMCN是平行四边形,由知,,可得,于是就有四边形BMCN是菱形,则.
本题考查了全等三角形的判定与性质,难度一般,对于此类题目要注意掌握三角形全等及菱形判定定理.
16.【答案】证明:于点D,于点E,
和均为直角三角形.
在和中,,
≌,
.
又,
,
,
.
解:,理由如下:
同可证出:≌,
.
又,
,
.
【解析】由于点D、于点E,可得出和均为直角三角形,由、即可证出≌,根据全等三角形的性质可得出,结合可得出,再利用角的计算可求出,即;
同可得出,结合可得出,即.
本题考查了全等三角形的判定与性质以及角的计算,解题的关键是:利用全等三角形的性质结合角的计算找出;利用全等三角形的性质结合角的计算找出.
17.【答案】解:,
,
,
在和中,
≌,
;
解:由得:≌,
,
,
平分,
.
【解析】此题考查全等三角形的判定和性质、角平分线的定义、三角形内角和定理,熟练掌握全等三角形的判定和性质定理是解题关键.
首先根据,通过,证得,然后根据全等三角形的判定定理证得≌,最后根据全等三角形的性质即可证得;
首先根据全等三角形的性质证得,然后根据三角形的内角和定理求出的度数,最后根据角平分线的定义即可求出的度数.
18.【答案】解:,,,
,
,,
,
在和中,
≌;
≌,
,,
.
【解析】本题考查了全等三角形的性质和判定,垂线的定义等知识点的应用,解此题的关键是推出证明和全等的三个条件.
根据垂直定义求出,根据等式性质求出,根据AAS证明≌;
根据全等三角形的对应边相等得到,,利用,即可解答.
19.【答案】解:当时,,,
又,
在和中,
≌.
,
.
,
故线段PC与线段PQ垂直.
若≌,
则,,
,
解得;
若≌,
则,,
,
解得;
故存在或使得与全等.
【解析】此题考查全等三角形的判定与性质,注意分类讨论思想的渗透.
利用SAS证得≌,得出,进一步得出得出结论即可;
由≌,分两种情况:,,,,建立方程组求得答案即可.
20.【答案】证明:
,
即,
在和中,
,,
≌ .
解:由题意可得:.
解:当点D运动到线段BC的中点时,,
点D是线段BC的中点,
,
,
,
.
或20.
【解析】
【分析】
本题考查的是全等三角形的判定与性质,
根据题意找出三角形全等的条件即可解答;
根据题意直接进行解答即可;
当点D运动到线段BC的中点时,,然后再进行解答即可.
根据题意直接进行解答即可.
【解答】
见答案;
解:由题意可得:或28.
故答案为68或20.
21.【答案】解:,,
,,
点D是斜边AB的中点,,
,
,
;
答:结论仍然成立,
证明:如图2,过D作于M,于N,
,
,,
点D是斜边AB的中点,
,,
,
四边形CNDM是正方形,
,
,
,
在与中,,
≌,,
;
如图3,
过D作于M,于N,
,
,,
点D是斜边AB的中点,
,,
,
四边形CNDM是正方形,
,
,
,
在与中,,
≌,,
.
【解析】根据三角形的中位线和正方形的性质即可得到结论;
如图2,过D作于M,于N,根据三角形的中位线大小在得到,推出四边形CNDM是正方形,得到,根据余角的性质得到,根据全等三角形的性质得到≌,于是得到结论;
如图3,过D作于M,于N,根据三角形的中位线大小在得到,推出四边形CNDM是正方形,得到,根据余角的性质得到,根据全等三角形的性质得到≌,于是得到结论.
本题考查了等腰直角三角形的性质,全等三角形的判定和性质,正方形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.
22.【答案】证明:直线m,直线m,
,
,
,
,
,
在和中,
,
≌,
,,
;
,
,
,
在和中,
,
≌,
,,
.
当t等于6、10或22时,与全等.
【解析】
【分析】
本题考查了全等三角形的判定与性质以及分类讨论的思想,可能会因考虑不全面而出错,是一道易错题.判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;得出是解题关键.
根据直线m,直线m得,而,根据等角的余角相等得,然后根据“AAS”可判断≌,则,,于是;
利用,则,得出,进而得出≌即可得出答案;
易证,,只需,就可得到与全等,然后只需根据点P和点Q不同位置进行分类讨论即可解决问题.
【解答】
解:见答案;
见答案;
当时,点P在AB上,点Q在AC上,
此时有,,,.
当即,也即时,
,,,
.
.
在和中,
,
与≌.
当时,点P在AB上,点Q也在AB上,
此时相当于两点相遇,则有,解得;
当时,点Q在点AB上,点P在AC上,当即,解得舍去;
当时,点Q停在点B的位置,点P在AC上,当即,解得,
综上所述:当t等于6、10或22时,与全等.
23.【答案】解:,
,
,,
,
为AB的中点,
,
,
,
在与中,
,
≌;
设点Q运动时间为t秒,运动速度为,
≌CPQ,
,,
,
;
设经过x秒后,点Q第一次追上点P,由题意得,
解得:,
点P运动的路程为,
,
此时点P在BC边上,
经过10秒,点Q第一次在BC边上追上点P.
【解析】本题考查了全等三角形的判定和性质,找准对应边是解题的关键.
根据等腰三角形的性质得到,再加上,,则可判断与全等;
设点Q的运动速度为,则,,,当≌,则,;然后分别建立关于t和v的方程,再解方程即可;
设经过x秒后,点Q第一次追上点P,由题意得,解方程得到点P运动的路程为,得到此时点P在BC边上,于是得到结果.
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
