探索勾股定理

(共23张PPT)
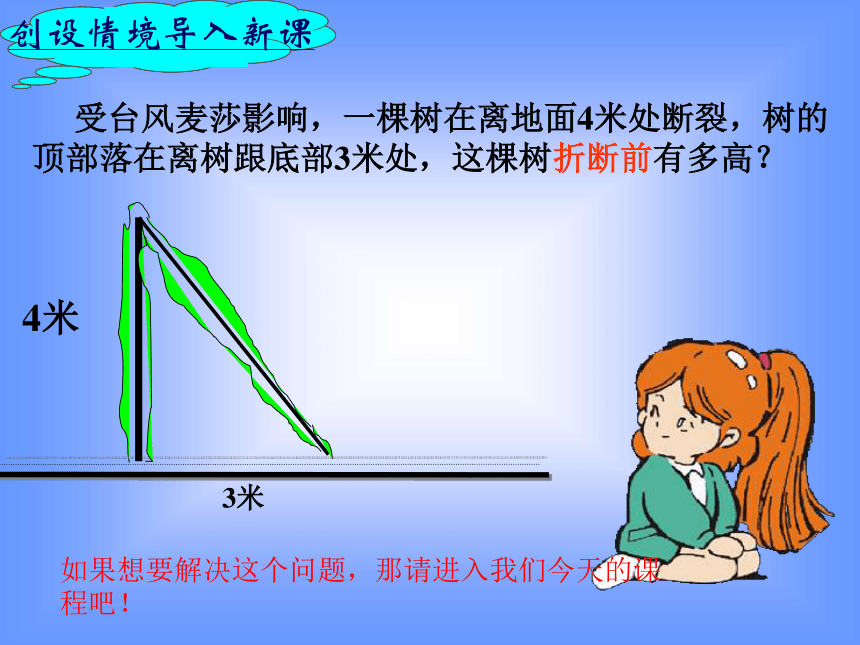
受台风麦莎影响，一棵树在离地面4米处断裂，树的
顶部落在离树跟底部3米处，这棵树折断前有多高？
y=0
创设情境导入新课
4米
3米
如果想要解决这个问题，那请进入我们今天的课程吧！
学习目标：
【知识与技能】能说出勾股定理,并能应用其进行简单的计算和实际运用.
【过程与方法】经历观察—猜想—归纳—验证的数学发现过程,发展合情推理的能力,体会数形结合和由特殊到一般的数学思想.
【情感态度与价值观】通过对勾股定理历史的了解和实例应用，体会勾股定理的文化价值；通过获得成功的经验和克服困难的经历，增进数学学习的信心.
二、教学重点与难点
重点：探索勾股定理.
难点：利用数形结合的方法验证勾股定理．
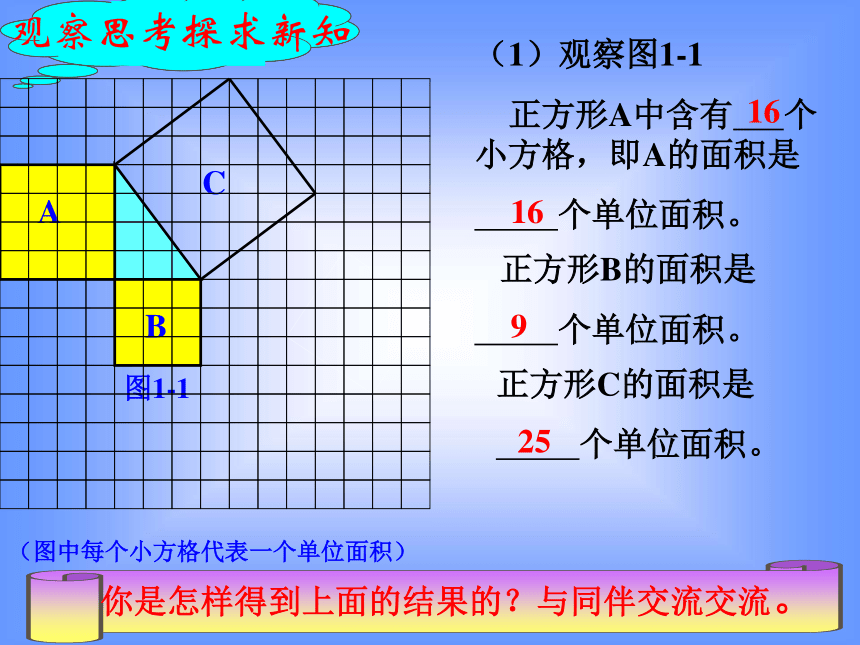
（1）观察图1-1
正方形A中含有 个小方格，即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
16
16
9
25
y=0
观察思考探求新知
你是怎样得到上面的结果的？与同伴交流交流。
A
B
C
图1-1
（图中每个小方格代表一个单位面积）
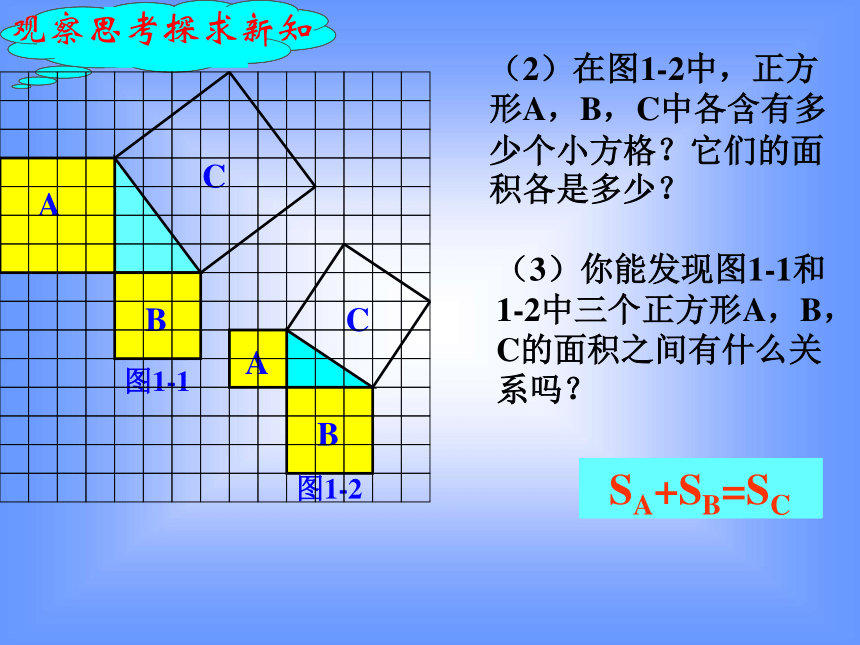
（2）在图1-2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？
（3）你能发现图1-1和1-2中三个正方形A，B，C的面积之间有什么关系吗？
SA+SB=SC
y=0
观察思考探求新知
A
B
C
图1-1
A
B
C
图1-2
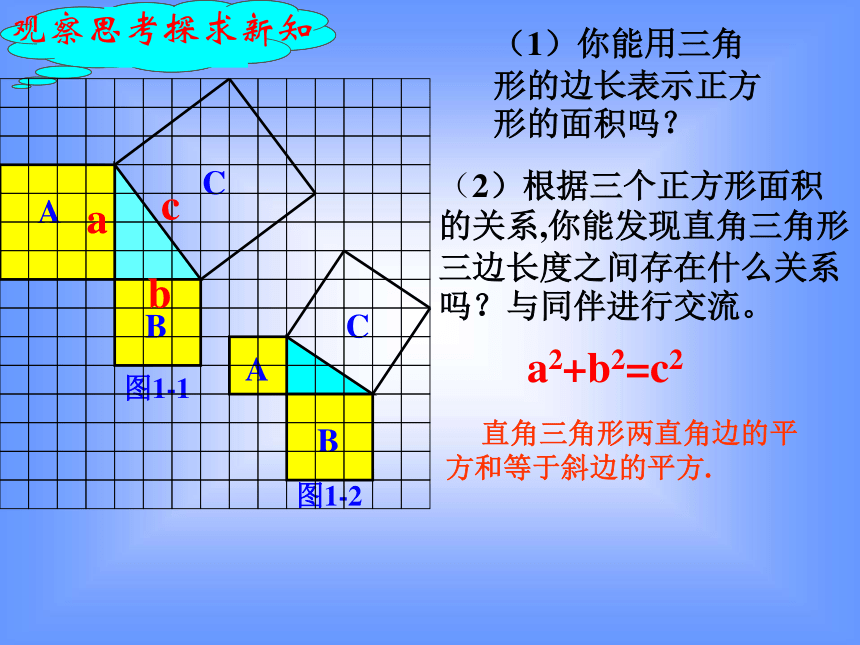
（1）你能用三角形的边长表示正方形的面积吗？
（2）根据三个正方形面积的关系,你能发现直角三角形三边长度之间存在什么关系吗？与同伴进行交流。
y=0
观察思考探求新知
直角三角形两直角边的平方和等于斜边的平方.
A
B
C
图1-1
A
B
C
图1-2
a
b
c
a2+b2=c2
动手操作 验证发现
分别以3厘米、4厘米为直角边作出一个直角三角形，并测量斜边的长度。上述规律对这个三角形仍然成立吗？
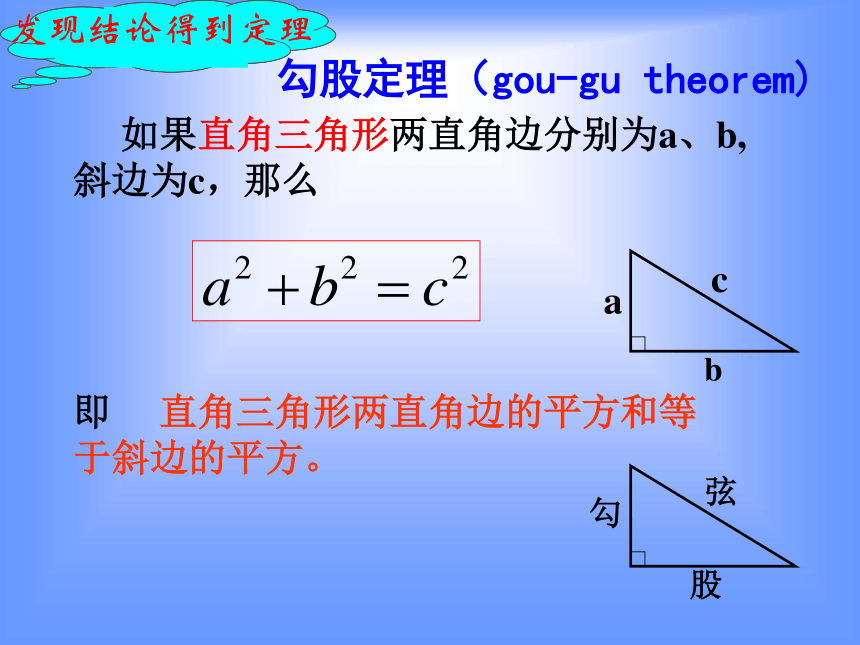
勾股定理（gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c，那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
y=0
发现结论得到定理
c
a
b
c
a
b
c
a
b
c
a
b
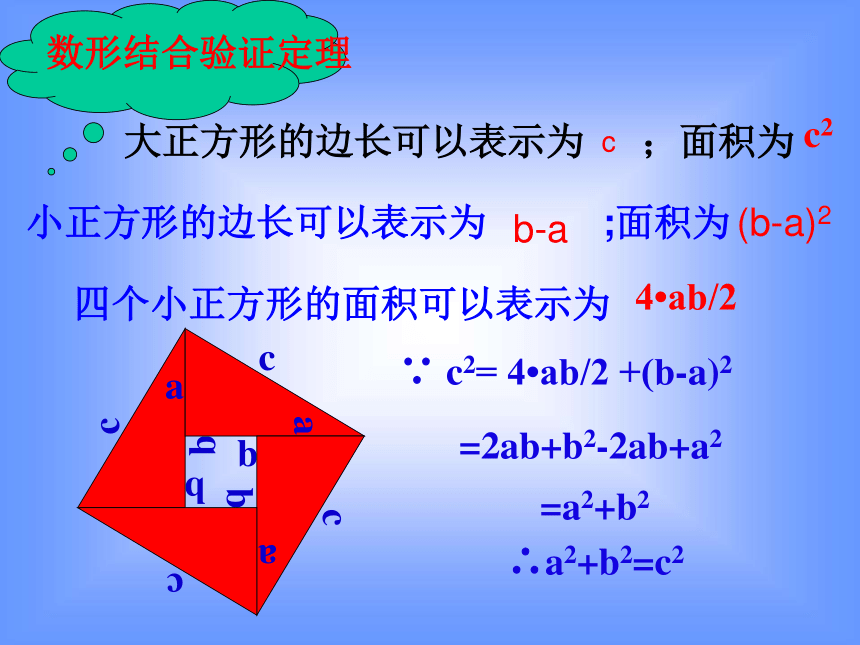
∵ c2= 4 ab/2 +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的边长可以表示为 ；面积为
c2
4 ab/2
数形结合验证定理
c
小正方形的边长可以表示为 ;面积为
b-a
(b-a)2
四个小正方形的面积可以表示为
y=0
b
a
b
b
c
c
c
c
b
a
a
a
证明结论验证定理
动动手
b
a
c
a
即a2+b2=c2
y=0
数形结合验证定理
c
c
a
b
c
4个
y=0
5
12
x
b
17
15
1、求下列用字母表示的边长
应用知识小试身手
1 .在△ABC中，∠C=90°，∠A,∠B,∠C的对边分别为a,b,c
(1)若a= 5,b=12, 则c=
(2)若a=24,c=25, 则b=
练习题
13
7
2．如图，阴影部分是一个半圆，则阴影部分的面积为　　　　　．（不取近似值）
3．底边长为16cm，底边上的高为6cm的等腰三角形的腰长为　　　　cm．
y=0
1、如图，受台风麦莎影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？
应用知识回归生活
4米
3米
2.如图，隔湖有两点A,B,从与BA方向成直角的BC方向上的点C,测CA=100m,CB=80m, 求AB的长．
A
B
C
5.如图所示，校园内有两棵树相距12m，一棵树高13m，另一棵树高8m，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞多少米？
13m
12m
8m
在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.
勾
股
两千多年前，古希腊有个哥拉
斯学派，他们首先发现了勾股定理，因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派，1955
勾 股 世 界
国家之一。早在三千多年前，
国家之一。早在三千多年前，
国家之一。早在三千多年前，
国家之一。早在三千多年前，
国家之一。早在三千多年前，
国家之一。早在三千多年前，
国家之一。早在三千多年前，
国家之一。早在三千多年前
两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票.
我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中.
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，
就把这一证法称为“总统”证法。
有趣的总统证法
一分耕耘，一分收获
你能告诉我这节课的收获吗？
y=0
（3）补充：阅读有关勾股定理的资料
总结反思布置作业
（1）P81 习题 第1、2、3题。(必做题)
（2）补充：如图,这是由两个边长分别为1、2的正方形连在一起的“L”
型纸片，现在请你剪两刀再将所得图形拼成一个正方形（A、B
层学生选做，C层学生必做）
http:///200406/ca488379.htm
http://www.cbe21.com/subject/maths/html/040602/2001_03/20010313_62.html
http://202.113.29.16/mengdj/wlkj/sxyx/gougu.htm
http://www.huangrong.org/gougu/page11.html