全等三角形
图片预览





文档简介
(共41张PPT)
义务教育课程标准实验教科书
八年级 上 册
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8
0 1 2 3 4 5
0 1 2 3 4 5
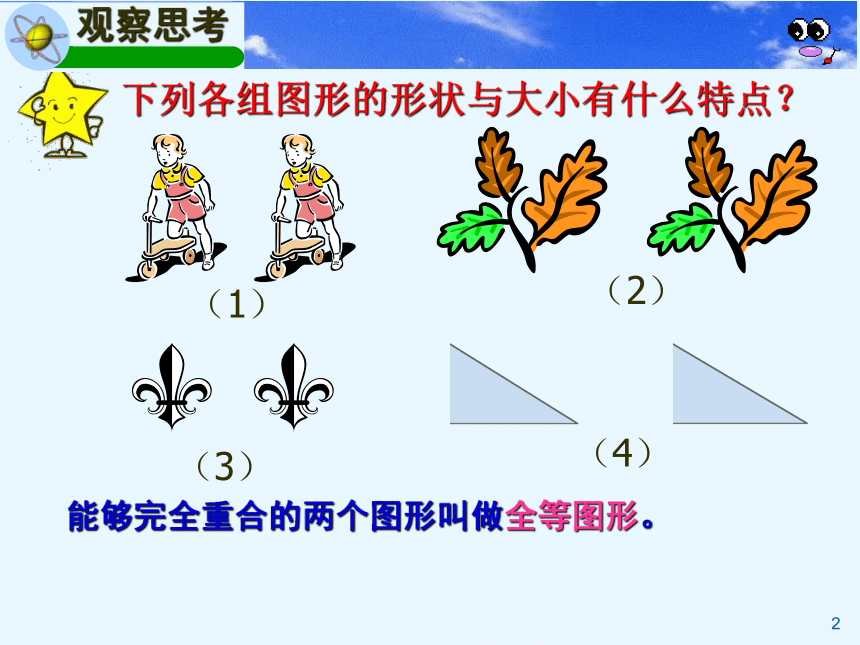
下列各组图形的形状与大小有什么特点?
能够完全重合的两个图形叫做全等图形。
(1)
(2)
(3)
(4)
观察思考
下列哪些图形是全等图形?
观察思考
全等图形的特征:
(1) 你还能说出生活中全等图形的例子吗
议一议
(2) 如果两个图形全等,它们的形状大小一定都相同吗?
全等形的形状和大小完全相同。
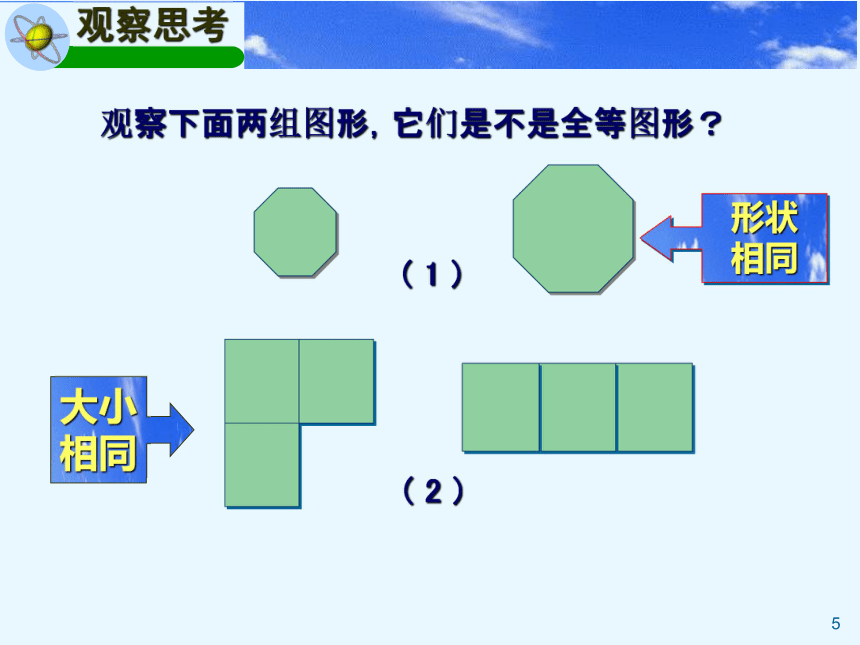
形状
相同
大小
相同
观察下面两组图形,它们是不是全等图形?
( 1 )
( 2 )
观察思考
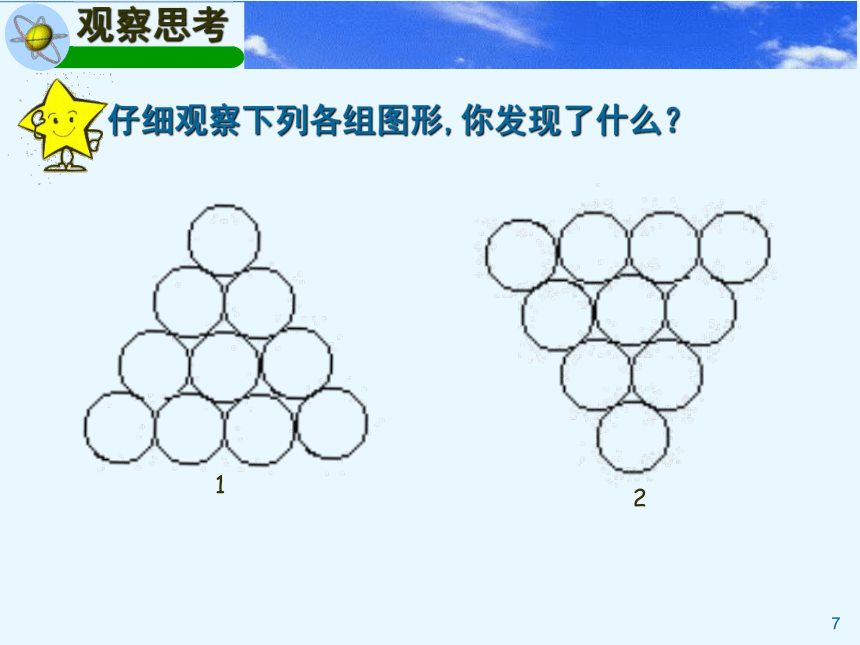
仔细观察下列各组图形,你发现了什么?
1
2
观察思考
1
2
仔细观察下列各组图形,你发现了什么?
观察思考
仔细观察下列各组图形,你发现了什么?
观察思考
一个图形经过平移,翻折,旋转后,位置变化了,但___和___都没有改变,即平移,翻折,旋转前后的图形__。
形状
大小
全等
根据刚才的图形回答:
A
C
B
A'
C'
B'
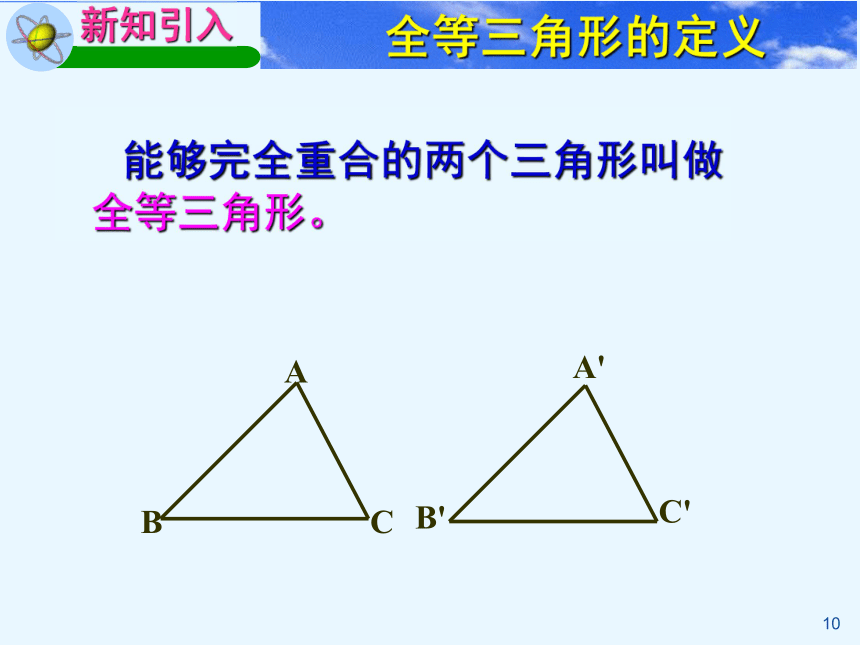
能够完全重合的两个三角形叫做全等三角形。
新知引入
全等三角形的定义
A
B
C
D
E
F
A
B
D
C
A
B
C
E
D
A
B
C
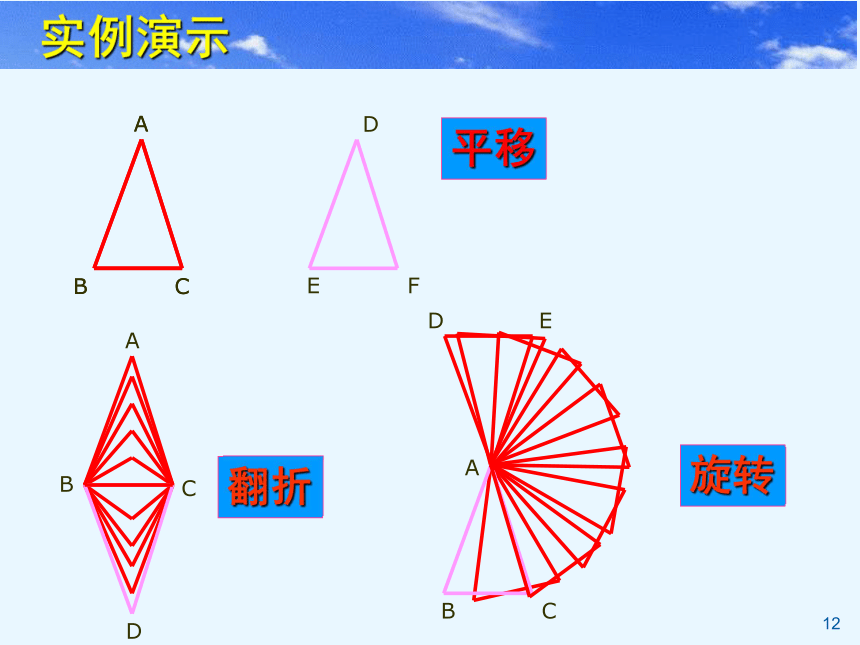
平移
翻折
旋转
实例演示
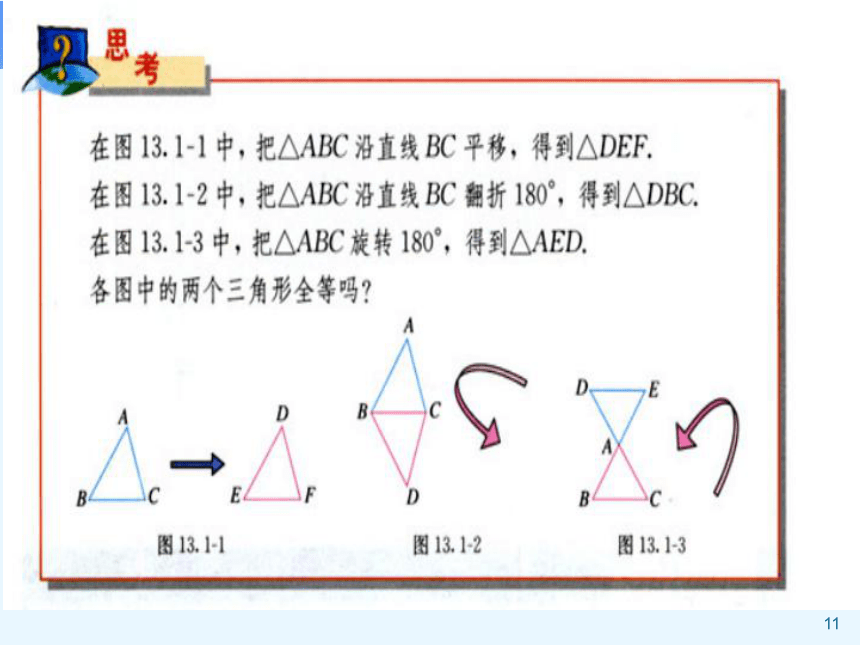
一个三角形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变, 即平移、翻折、旋转前后的三角形全等.
把两个全等的三角形重叠到一起
重合的顶点叫做对应顶点;
重合的边叫做对应边;
重合的角叫做对应角。
你能指出上面两个全等三角形的对应顶点、对应边、对应角吗?
A
B
C
D
E
F
A
B
C
理解概念
对应顶点、对应边、对应角
△ABC全等于△DEF可表示为:
△ABC △DEF
注意:表示时通常把对应顶点的字母写在对应的位置上。
≌
A
B
C
D
E
F
A
B
C
全等三角形的记法
新知引入
A
B
C
D
△ABC ≌
△DCB
理解新知
D
E
F
A
B
C
△ABC ≌
△DEF
理解新知
B
D
A
C
O
△AOC ≌
△BOD
理解新知
A
B
C
D
△ABC ≌
△CDA
理解新知
C
D
A
B
E
△ADC ≌
△AEB
理解新知
A
B
C
D
△ABC ≌
△DBC
理解新知
A
B
C
D
E
A
B
C
D
△ABC≌△DBC
△ABC≌△AED
理解新知
思考:能否根据全等式说出两个全等三角形的对应边和对应角?
对应边:DM和AE,DN和AH,MN和EH,
对应角:∠D和∠A,∠M和∠E,∠N和∠H。
例如:由△DMN≌△AEH可知,
注意:在具体图形中,有时角不能只用一个大写字母表示。
理解新知
全等三角形的对应边有什么关系?
全等三角形的对应角有什么关系?
结论:全等三角形的对应边相等;
全等三角形的对应角相等。
A
B
C
D
E
F
新知引入
全等三角形的性质
全等三角形的性质
(全等三角形的对应边相等)
(全等三角形的对应角相等)
全等三角形的对应边相等,
全等三角形的对应角相等。
∵△ABC≌ △A’B’C’(已知)
∴ AB=A’B’, BC=B’C’, AC=A’C’
∴ ∠ A= ∠ A’, ∠ B= ∠B’ ,
∠ C= ∠C’
角
角
角
边
边
边
AB=DF
AC=DE
BC=EF
∠BAC=∠EDF
∠B=∠F
∠C=∠E
A
B
C
D
F
E
△ABC≌△DFE
角
角
角
边
边
边
AC=BD
MC=MD
AM=BM
∠A=∠B
∠C=∠D
∠AMC=∠BMD
△___≌△___
AMC
BMD
图中能用字母表示
的全等三角形是:
(较短的)
(较长的)
(较小的)
(较大的)
方法提练
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)最大的边是对应边,最小的边也是对应边;
(5)最大的角是对应角,最小的角也是对应角;
4)周长相等的三角形是全等三角形。 ( )
2)全等三角形的周长相等,面积也相等。 ( )
1、若△ ABC ≌ △ DEF,则∠B=40 , ∠C=60 ,则∠D= .
80
√
√
X
X
2、判断题 1)全等三角形的对应边相等,对应角相等( )
3)面积相等的三角形是全等三角形。 ( )
3、如图,△ABC≌△ADE,
若∠D=45°,∠C=75°,
则∠DAE=_____。
A
B
C
D
E
4、如图,△ABD≌△CDB,
若AB=4,AD=5,BD=6,则BC=____,CD=____.
A
B
C
D
60°
4
5
A
B
C
D
E
O
5、△ABD≌△ACE,若∠B=25°,BD=6㎝,AD=4㎝,你能得出△ACE中哪些角的大小,哪些边的长度吗?为什么 ?
解:∵△ABD≌△ACE
∴∠C=∠B=25°(全等三角形对应角相等)
∴CE=BD=6cm
AE=AD=4cm(全等三角形对应边相等)
6、已知,△ABC≌△DEF,若AB=5,BC=6,AC=7,∠D=40°,∠C=80°,
则EF=____ ,∠A=____,∠E=____。
7、如图,△ABD≌△EBC,AB=3cm,BC=5cm,求DE的长.
A
B
C
E
D
解:∵△ABD≌△EBC
∴AB=EB、BD=BC
∴DE=BD-EB
=BC-AB
=5-3=2cm
40°
60°
6
8、如右图,已知△ABD≌△ACE, 且∠C=45°,AC = 5,AE = 3,则 ∠B = , DC = .
A
E
B
C
D
2
45°
3
5
3
9、如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD对应角,且∠BAC=25°, ∠B=35°,AB=3cm,BC=1cm,求出∠E, ∠ ADE的度数和线段DE,AE 的长度。
B
C
E
D
A
解:∵ △ABC≌△AED,(已知)
∴∠E= ∠B= 35°(全等三角形对应角相等)
∠ADE=∠ACB=18O°- 25°- 35°
=120° (全等三角形对应角相等)
DE=BC=1cm, AE=AB=3cm
(全等三角形对应边相等)
10、如图,△ABC≌△DEC,CA和CD,CB和CE是对应边, ∠ ACD和∠BCE相等吗?为什么?
D
B
E
A
C
因为 △ABC≌△DEC,
所以 ∠ DCE =∠ACB
又因为
∠ACD = ∠DCE - ∠ 1
∠BCE = ∠ACB - ∠ 1
所以 ∠ ACD = ∠BCE
1
11.如图,长方形ABCD沿AM折叠,使D点落在BC上的N点处,已知AD=7cm,DM=3cm, ∠DAM=39°,则AN=___cm, NM=___cm, ∠NAM=___.
7cm
3cm
)39°
7
3
39°
A
B
C
D
M
N
12.如图:⊿ADC≌⊿BFE,∠E=∠C,AB=7,DF=3,求AF的长?
A
B
C
E
F
D
解:因为 ⊿ADC≌⊿BFE
所以 AD=BF
(全等三角形对应边相等)
所以 AD-DF=BF-DF(等式性质)
即 AF=BD
AF=BD=1/2(AB-DF)
=1/2(7-2)
=2
拓展与延伸
13、下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?
1、回忆这节课,学习了全等三角形的哪些知识?
(1)全等三角形的概念:
能完全重合的两个三角形是全等三角形,
(2)表示方法:用符号≌来表示.
(3)对应写法:对应顶点写在对应位置.
(4)性质:全等三角形的对应边相等,对应角相等.
2、找全等三角形对应边、对应角的方法。
3、利用全等三角形求某些线段的长度或角的大小。
谢谢同学们!
义务教育课程标准实验教科书
八年级 上 册
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8
0 1 2 3 4 5
0 1 2 3 4 5
下列各组图形的形状与大小有什么特点?
能够完全重合的两个图形叫做全等图形。
(1)
(2)
(3)
(4)
观察思考
下列哪些图形是全等图形?
观察思考
全等图形的特征:
(1) 你还能说出生活中全等图形的例子吗
议一议
(2) 如果两个图形全等,它们的形状大小一定都相同吗?
全等形的形状和大小完全相同。
形状
相同
大小
相同
观察下面两组图形,它们是不是全等图形?
( 1 )
( 2 )
观察思考
仔细观察下列各组图形,你发现了什么?
1
2
观察思考
1
2
仔细观察下列各组图形,你发现了什么?
观察思考
仔细观察下列各组图形,你发现了什么?
观察思考
一个图形经过平移,翻折,旋转后,位置变化了,但___和___都没有改变,即平移,翻折,旋转前后的图形__。
形状
大小
全等
根据刚才的图形回答:
A
C
B
A'
C'
B'
能够完全重合的两个三角形叫做全等三角形。
新知引入
全等三角形的定义
A
B
C
D
E
F
A
B
D
C
A
B
C
E
D
A
B
C
平移
翻折
旋转
实例演示
一个三角形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变, 即平移、翻折、旋转前后的三角形全等.
把两个全等的三角形重叠到一起
重合的顶点叫做对应顶点;
重合的边叫做对应边;
重合的角叫做对应角。
你能指出上面两个全等三角形的对应顶点、对应边、对应角吗?
A
B
C
D
E
F
A
B
C
理解概念
对应顶点、对应边、对应角
△ABC全等于△DEF可表示为:
△ABC △DEF
注意:表示时通常把对应顶点的字母写在对应的位置上。
≌
A
B
C
D
E
F
A
B
C
全等三角形的记法
新知引入
A
B
C
D
△ABC ≌
△DCB
理解新知
D
E
F
A
B
C
△ABC ≌
△DEF
理解新知
B
D
A
C
O
△AOC ≌
△BOD
理解新知
A
B
C
D
△ABC ≌
△CDA
理解新知
C
D
A
B
E
△ADC ≌
△AEB
理解新知
A
B
C
D
△ABC ≌
△DBC
理解新知
A
B
C
D
E
A
B
C
D
△ABC≌△DBC
△ABC≌△AED
理解新知
思考:能否根据全等式说出两个全等三角形的对应边和对应角?
对应边:DM和AE,DN和AH,MN和EH,
对应角:∠D和∠A,∠M和∠E,∠N和∠H。
例如:由△DMN≌△AEH可知,
注意:在具体图形中,有时角不能只用一个大写字母表示。
理解新知
全等三角形的对应边有什么关系?
全等三角形的对应角有什么关系?
结论:全等三角形的对应边相等;
全等三角形的对应角相等。
A
B
C
D
E
F
新知引入
全等三角形的性质
全等三角形的性质
(全等三角形的对应边相等)
(全等三角形的对应角相等)
全等三角形的对应边相等,
全等三角形的对应角相等。
∵△ABC≌ △A’B’C’(已知)
∴ AB=A’B’, BC=B’C’, AC=A’C’
∴ ∠ A= ∠ A’, ∠ B= ∠B’ ,
∠ C= ∠C’
角
角
角
边
边
边
AB=DF
AC=DE
BC=EF
∠BAC=∠EDF
∠B=∠F
∠C=∠E
A
B
C
D
F
E
△ABC≌△DFE
角
角
角
边
边
边
AC=BD
MC=MD
AM=BM
∠A=∠B
∠C=∠D
∠AMC=∠BMD
△___≌△___
AMC
BMD
图中能用字母表示
的全等三角形是:
(较短的)
(较长的)
(较小的)
(较大的)
方法提练
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)最大的边是对应边,最小的边也是对应边;
(5)最大的角是对应角,最小的角也是对应角;
4)周长相等的三角形是全等三角形。 ( )
2)全等三角形的周长相等,面积也相等。 ( )
1、若△ ABC ≌ △ DEF,则∠B=40 , ∠C=60 ,则∠D= .
80
√
√
X
X
2、判断题 1)全等三角形的对应边相等,对应角相等( )
3)面积相等的三角形是全等三角形。 ( )
3、如图,△ABC≌△ADE,
若∠D=45°,∠C=75°,
则∠DAE=_____。
A
B
C
D
E
4、如图,△ABD≌△CDB,
若AB=4,AD=5,BD=6,则BC=____,CD=____.
A
B
C
D
60°
4
5
A
B
C
D
E
O
5、△ABD≌△ACE,若∠B=25°,BD=6㎝,AD=4㎝,你能得出△ACE中哪些角的大小,哪些边的长度吗?为什么 ?
解:∵△ABD≌△ACE
∴∠C=∠B=25°(全等三角形对应角相等)
∴CE=BD=6cm
AE=AD=4cm(全等三角形对应边相等)
6、已知,△ABC≌△DEF,若AB=5,BC=6,AC=7,∠D=40°,∠C=80°,
则EF=____ ,∠A=____,∠E=____。
7、如图,△ABD≌△EBC,AB=3cm,BC=5cm,求DE的长.
A
B
C
E
D
解:∵△ABD≌△EBC
∴AB=EB、BD=BC
∴DE=BD-EB
=BC-AB
=5-3=2cm
40°
60°
6
8、如右图,已知△ABD≌△ACE, 且∠C=45°,AC = 5,AE = 3,则 ∠B = , DC = .
A
E
B
C
D
2
45°
3
5
3
9、如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD对应角,且∠BAC=25°, ∠B=35°,AB=3cm,BC=1cm,求出∠E, ∠ ADE的度数和线段DE,AE 的长度。
B
C
E
D
A
解:∵ △ABC≌△AED,(已知)
∴∠E= ∠B= 35°(全等三角形对应角相等)
∠ADE=∠ACB=18O°- 25°- 35°
=120° (全等三角形对应角相等)
DE=BC=1cm, AE=AB=3cm
(全等三角形对应边相等)
10、如图,△ABC≌△DEC,CA和CD,CB和CE是对应边, ∠ ACD和∠BCE相等吗?为什么?
D
B
E
A
C
因为 △ABC≌△DEC,
所以 ∠ DCE =∠ACB
又因为
∠ACD = ∠DCE - ∠ 1
∠BCE = ∠ACB - ∠ 1
所以 ∠ ACD = ∠BCE
1
11.如图,长方形ABCD沿AM折叠,使D点落在BC上的N点处,已知AD=7cm,DM=3cm, ∠DAM=39°,则AN=___cm, NM=___cm, ∠NAM=___.
7cm
3cm
)39°
7
3
39°
A
B
C
D
M
N
12.如图:⊿ADC≌⊿BFE,∠E=∠C,AB=7,DF=3,求AF的长?
A
B
C
E
F
D
解:因为 ⊿ADC≌⊿BFE
所以 AD=BF
(全等三角形对应边相等)
所以 AD-DF=BF-DF(等式性质)
即 AF=BD
AF=BD=1/2(AB-DF)
=1/2(7-2)
=2
拓展与延伸
13、下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?
1、回忆这节课,学习了全等三角形的哪些知识?
(1)全等三角形的概念:
能完全重合的两个三角形是全等三角形,
(2)表示方法:用符号≌来表示.
(3)对应写法:对应顶点写在对应位置.
(4)性质:全等三角形的对应边相等,对应角相等.
2、找全等三角形对应边、对应角的方法。
3、利用全等三角形求某些线段的长度或角的大小。
谢谢同学们!
