全等三角形学案
图片预览

文档简介
第 十 一 章 全 等 三 角 形
11.1 全等三角形
一、学习目标
1、了解全等三角形的有关概念,理解并掌握全等三角形的性质;
2、能够准确辩认全等三角形的对应元素(对应顶点、对应边、对应角);
3、经历观察、分析、比较、操作、发现等过程,培养识图能力及审美意识.
二、学习重点:全等三角形性质的应用及准确辩认全等三角形的对应边、对应角.
三、学法指导:通过观察思考,动手操作,参与概念的形成过程;仔细识图,尝试总
结规律,逐步培养归纳、概括能力.
四、学习过程
【课前准备及预习感悟】
1、对于两条线段或两个角来说:
如果它们的大小相等,那么放在一起能够 ;
如果它们放在一起能够重合,那么它们的大小 .
1、全等形、全等三角形的有关概念
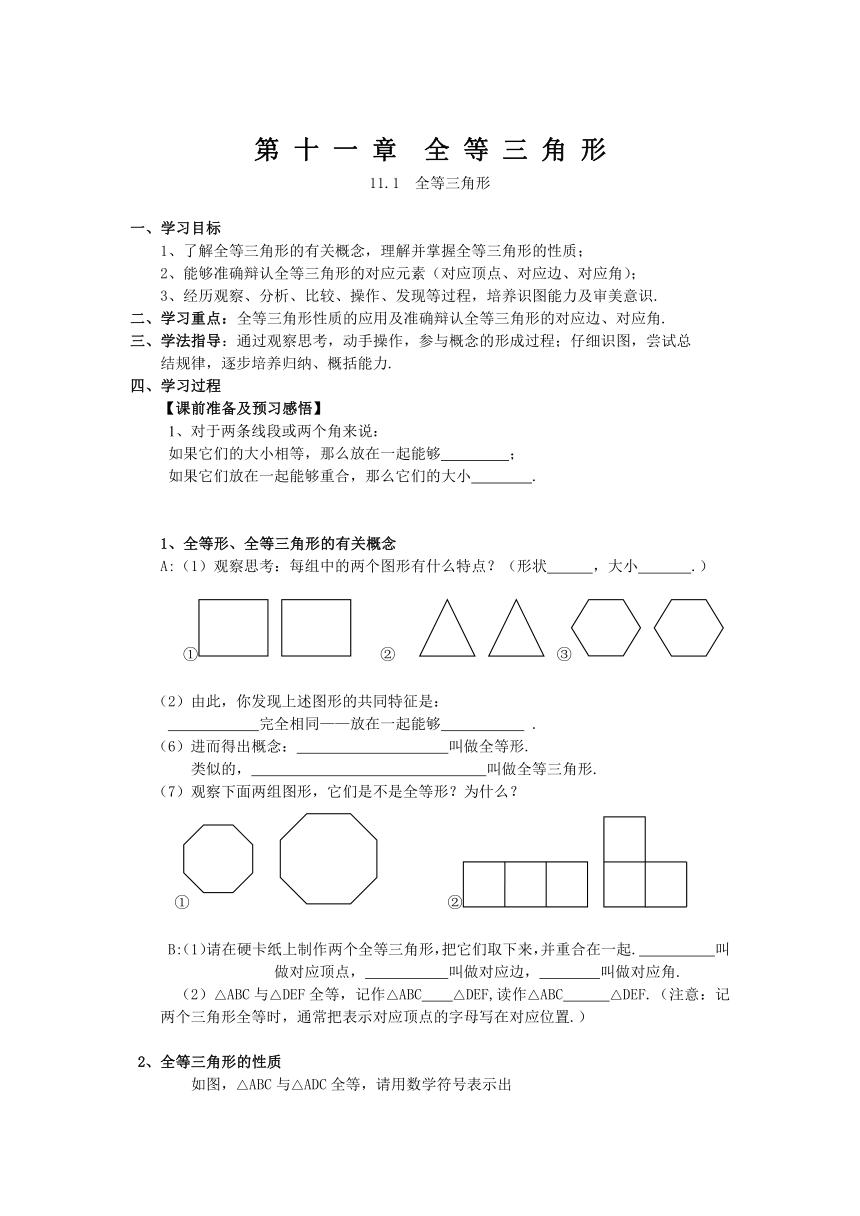
A:(1)观察思考:每组中的两个图形有什么特点?(形状 ,大小 .)
① ② ③
(2)由此,你发现上述图形的共同特征是:
完全相同——放在一起能够 .
(6)进而得出概念: 叫做全等形.
类似的, 叫做全等三角形.
(7)观察下面两组图形,它们是不是全等形?为什么?
① ②
B:(1)请在硬卡纸上制作两个全等三角形,把它们取下来,并重合在一起. 叫做对应顶点, 叫做对应边, 叫做对应角.
(2)△ABC与△DEF全等,记作△ABC △DEF,读作△ABC △DEF.(注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应位置.)
2、全等三角形的性质
如图,△ABC与△ADC全等,请用数学符号表示出
这两个三角形全等,并写出相等的边和角.
3、确定全等三角形的对应边、对应角
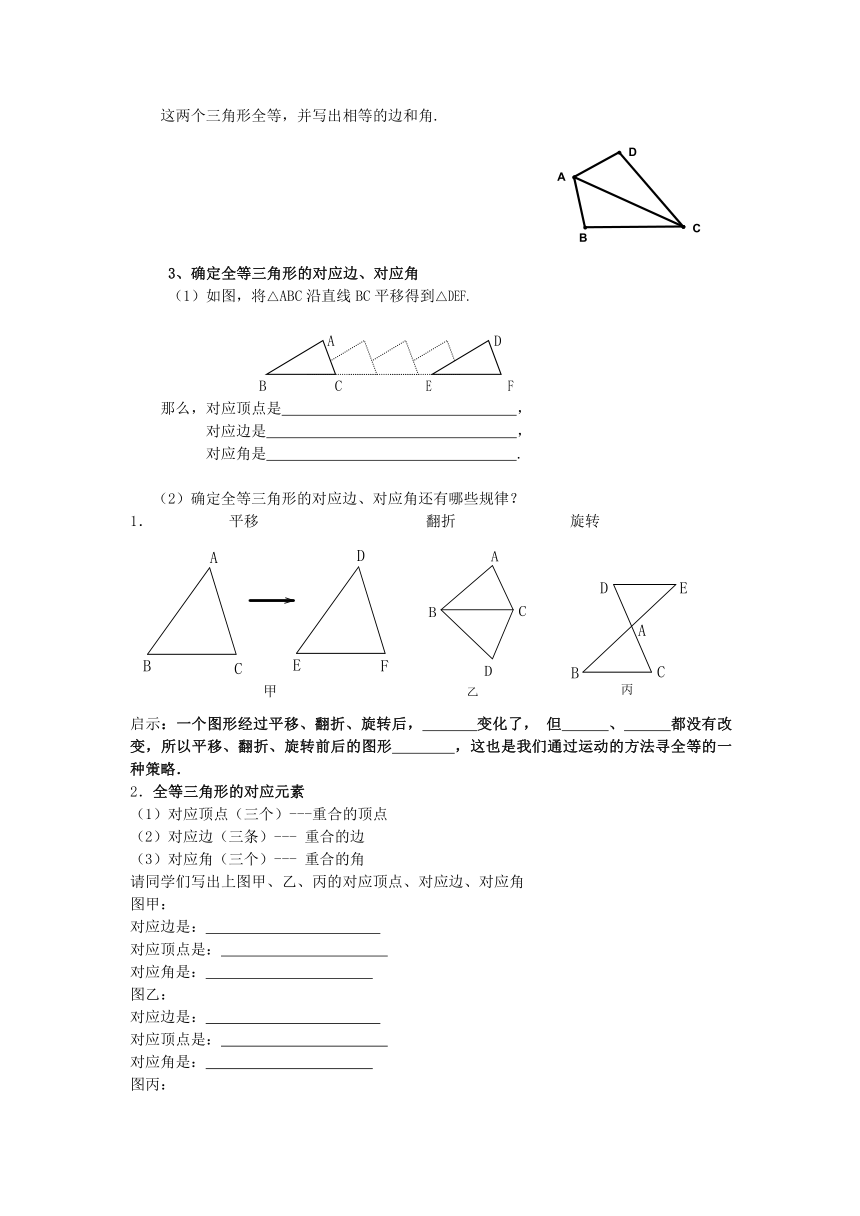
(1)如图,将△ABC沿直线BC平移得到△DEF.
A D
B C E F
那么,对应顶点是 ,
对应边是 ,
对应角是 .
(2)确定全等三角形的对应边、对应角还有哪些规律?
1. 平移 翻折 旋转
启示:一个图形经过平移、翻折、旋转后, 变化了,但 、 都没有改变,所以平移、翻折、旋转前后的图形 ,这也是我们通过运动的方法寻全等的一种策略.
2.全等三角形的对应元素
(1)对应顶点(三个)---重合的顶点
(2)对应边(三条)--- 重合的边
(3)对应角(三个)--- 重合的角
请同学们写出上图甲、乙、丙的对应顶点、对应边、对应角
图甲:
对应边是:
对应顶点是:
对应角是:
图乙:
对应边是:
对应顶点是:
对应角是:
图丙:
对应边是:
对应顶点是:
对应角是:
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(5)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角。
3.“全等”用“≌”表示,读作“全等于”
如图甲记作:△ABC≌△DEF 读作:△ABC全等于△DEF
如图乙记作: 读作:
如图丙记作: 读作:
注意:两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
三、全等三角形的性质
全等三角形的性质:
全等三角形的 相等, 相等.
【知识应用与能力形成】
例1 已知△ABC≌△DFE, ∠A=960, ∠B=250,DF=10cm,求∠E的度数及AB的长.
例题反思:
例2 如图,已知△ABC≌△AEF,∠B=∠E,AB=AE,
(1)请写出其它的对应边、对应角;(2)∠BAE=∠CAF吗 为什么
【基础与达标】
1、下列说法:①全等三角形的对应边相等,对应角相等;②全等三角形的周长相等,面积也相等;③面积相等的三角形是全等三角形;④周长相等的三角形是全等三角形,正确的说法是( )
A ②③ B ③④ C ①② D ①②③
2、△ABC≌△DEF,∠A的对应角是∠D,∠B的对应角∠E,则∠C与_______是对应角;AB与_______是对应边,BC与_______是对应边,AC与_______是对应边.
3、如图△ ABD ≌ △CDB,
若AB=4,AD=5,BD=6,
求BC、CD的长.
课堂检测:
(一)
1、能够______________的图形就是全等图形, 两个全等图形的_________和________完全相同。
2、一个图形经过______、______、_________后所得的图形与原图形 。
3、把两个全等的三角形重合在一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 。“全等”用“ ”表示,读作 。
4、如图所示,△OCA≌△OBD,
对应顶点有:点___和点___,点___和点___,点___和点___;
对应角有:____和____,_____和_____,_____和_____;
对应边有:____和____,____和____,_____和_____.
5、全等三角形的性质:全等三角形的 相等, 相等。
(二)、练一练
1.如图,△ABC≌△CDA,AB和CD,BC和DA是对应边。写出其他对应边及对应角。
2如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边。写出其他对应边及对应角。
《课内探究》
1.如图△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.
在△NMH中,MH是最长边.EF=2.1㎝,EH=1.1㎝,HN=3.3㎝.
(1)写出其他对应边及对应角.
(2)求线段MN及线段HG的长.
2.如图,△ABC≌△DEC,CA和CD,CB和CE是对应边.∠ACD和∠BCE相等吗?
为什么?
《课后训练》
1. 如图所示,若△OAD≌△OBC,∠O=65°,∠C=20°,则∠OAD= .
第1题图 第2题图
2. 如图,若△ABC≌△DEF,回答下列问题:
(1)若△ABC的周长为17 cm,BC=6 cm,DE=5 cm,则DF = cm
(2)若∠A =50°,∠E=75°,则∠B=
3. 如图,△AOB≌△COD,那么∠ABD与∠CDB相等吗?为什么?
第3题图
﹡4. 如图:Rt△ABC中,∠ A=90°,若△ADB≌△EDB≌△EDC,则∠C=
B
D
O
A
C
11.1 全等三角形
一、学习目标
1、了解全等三角形的有关概念,理解并掌握全等三角形的性质;
2、能够准确辩认全等三角形的对应元素(对应顶点、对应边、对应角);
3、经历观察、分析、比较、操作、发现等过程,培养识图能力及审美意识.
二、学习重点:全等三角形性质的应用及准确辩认全等三角形的对应边、对应角.
三、学法指导:通过观察思考,动手操作,参与概念的形成过程;仔细识图,尝试总
结规律,逐步培养归纳、概括能力.
四、学习过程
【课前准备及预习感悟】
1、对于两条线段或两个角来说:
如果它们的大小相等,那么放在一起能够 ;
如果它们放在一起能够重合,那么它们的大小 .
1、全等形、全等三角形的有关概念
A:(1)观察思考:每组中的两个图形有什么特点?(形状 ,大小 .)
① ② ③
(2)由此,你发现上述图形的共同特征是:
完全相同——放在一起能够 .
(6)进而得出概念: 叫做全等形.
类似的, 叫做全等三角形.
(7)观察下面两组图形,它们是不是全等形?为什么?
① ②
B:(1)请在硬卡纸上制作两个全等三角形,把它们取下来,并重合在一起. 叫做对应顶点, 叫做对应边, 叫做对应角.
(2)△ABC与△DEF全等,记作△ABC △DEF,读作△ABC △DEF.(注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应位置.)
2、全等三角形的性质
如图,△ABC与△ADC全等,请用数学符号表示出
这两个三角形全等,并写出相等的边和角.
3、确定全等三角形的对应边、对应角
(1)如图,将△ABC沿直线BC平移得到△DEF.
A D
B C E F
那么,对应顶点是 ,
对应边是 ,
对应角是 .
(2)确定全等三角形的对应边、对应角还有哪些规律?
1. 平移 翻折 旋转
启示:一个图形经过平移、翻折、旋转后, 变化了,但 、 都没有改变,所以平移、翻折、旋转前后的图形 ,这也是我们通过运动的方法寻全等的一种策略.
2.全等三角形的对应元素
(1)对应顶点(三个)---重合的顶点
(2)对应边(三条)--- 重合的边
(3)对应角(三个)--- 重合的角
请同学们写出上图甲、乙、丙的对应顶点、对应边、对应角
图甲:
对应边是:
对应顶点是:
对应角是:
图乙:
对应边是:
对应顶点是:
对应角是:
图丙:
对应边是:
对应顶点是:
对应角是:
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(5)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角。
3.“全等”用“≌”表示,读作“全等于”
如图甲记作:△ABC≌△DEF 读作:△ABC全等于△DEF
如图乙记作: 读作:
如图丙记作: 读作:
注意:两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
三、全等三角形的性质
全等三角形的性质:
全等三角形的 相等, 相等.
【知识应用与能力形成】
例1 已知△ABC≌△DFE, ∠A=960, ∠B=250,DF=10cm,求∠E的度数及AB的长.
例题反思:
例2 如图,已知△ABC≌△AEF,∠B=∠E,AB=AE,
(1)请写出其它的对应边、对应角;(2)∠BAE=∠CAF吗 为什么
【基础与达标】
1、下列说法:①全等三角形的对应边相等,对应角相等;②全等三角形的周长相等,面积也相等;③面积相等的三角形是全等三角形;④周长相等的三角形是全等三角形,正确的说法是( )
A ②③ B ③④ C ①② D ①②③
2、△ABC≌△DEF,∠A的对应角是∠D,∠B的对应角∠E,则∠C与_______是对应角;AB与_______是对应边,BC与_______是对应边,AC与_______是对应边.
3、如图△ ABD ≌ △CDB,
若AB=4,AD=5,BD=6,
求BC、CD的长.
课堂检测:
(一)
1、能够______________的图形就是全等图形, 两个全等图形的_________和________完全相同。
2、一个图形经过______、______、_________后所得的图形与原图形 。
3、把两个全等的三角形重合在一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 。“全等”用“ ”表示,读作 。
4、如图所示,△OCA≌△OBD,
对应顶点有:点___和点___,点___和点___,点___和点___;
对应角有:____和____,_____和_____,_____和_____;
对应边有:____和____,____和____,_____和_____.
5、全等三角形的性质:全等三角形的 相等, 相等。
(二)、练一练
1.如图,△ABC≌△CDA,AB和CD,BC和DA是对应边。写出其他对应边及对应角。
2如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边。写出其他对应边及对应角。
《课内探究》
1.如图△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.
在△NMH中,MH是最长边.EF=2.1㎝,EH=1.1㎝,HN=3.3㎝.
(1)写出其他对应边及对应角.
(2)求线段MN及线段HG的长.
2.如图,△ABC≌△DEC,CA和CD,CB和CE是对应边.∠ACD和∠BCE相等吗?
为什么?
《课后训练》
1. 如图所示,若△OAD≌△OBC,∠O=65°,∠C=20°,则∠OAD= .
第1题图 第2题图
2. 如图,若△ABC≌△DEF,回答下列问题:
(1)若△ABC的周长为17 cm,BC=6 cm,DE=5 cm,则DF = cm
(2)若∠A =50°,∠E=75°,则∠B=
3. 如图,△AOB≌△COD,那么∠ABD与∠CDB相等吗?为什么?
第3题图
﹡4. 如图:Rt△ABC中,∠ A=90°,若△ADB≌△EDB≌△EDC,则∠C=
B
D
O
A
C
