6.5一次函数的应用 同步练习(含解析)
文档属性
| 名称 | 6.5一次函数的应用 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-25 06:59:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
5 一次函数的应用
知识能力全练
知识点一 利用一次函数解决实际问题
1.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内剩余油量Q(升)与行驶时间t(时)的关系式为( )
A.Q=5t B.Q=5t+40 C.Q=40-5t(0≤t≤8) D.以上答案都不对
2.如图所示,0A,BA分别表示甲、乙两名运动员运动的路程s(米)与时间t(秒)间的关系,则甲的速度比乙的速度每秒快( )
A.2.5米 B.2米 C.1.5米 D.1米
3.我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费方式,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水20吨,则应交水费_________元.
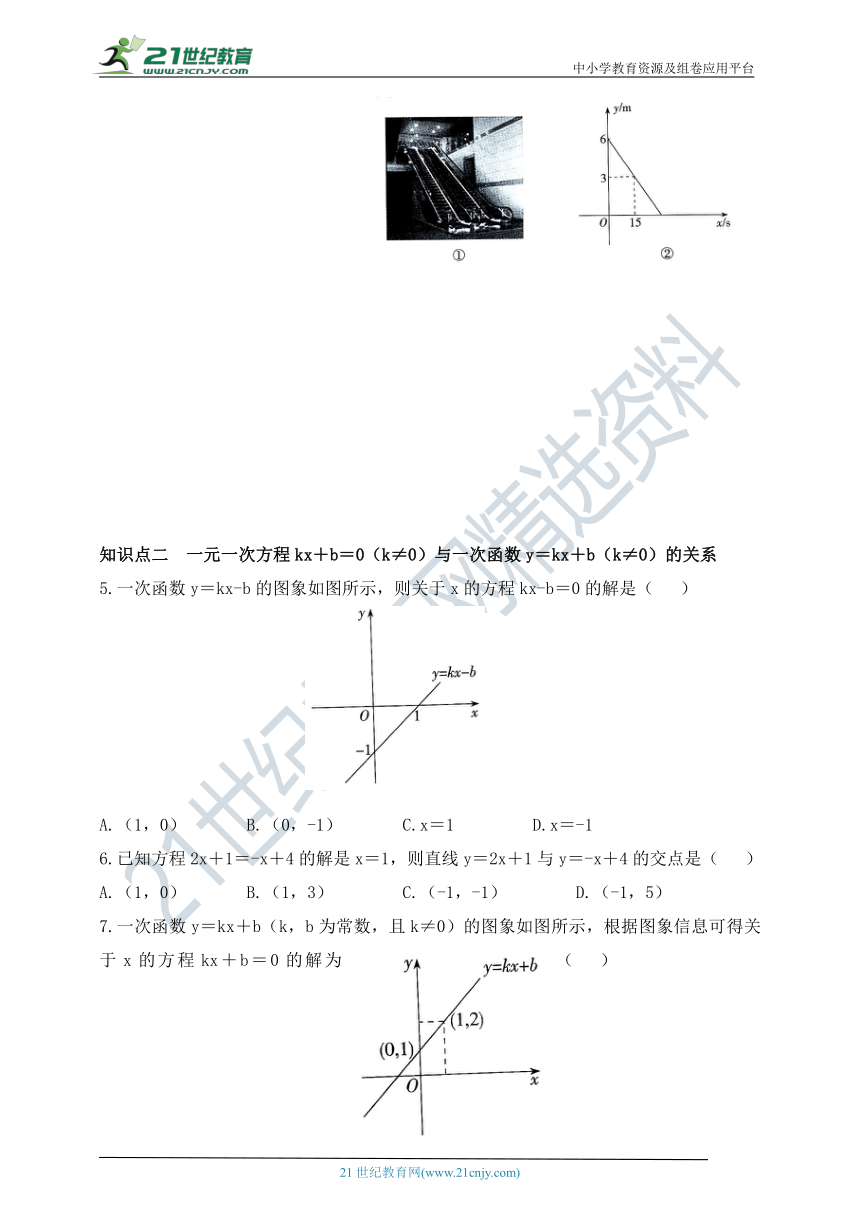
4.如图①,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系,乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图②所示.
(1)求y关于x的函数解析式;
(2)请通过计算说明甲、乙两人谁先到达一楼地面.
知识点二 一元一次方程kx+b=0(k≠0)与一次函数y=kx+b(k≠0)的关系
5.一次函数y=kx-b的图象如图所示,则关于x的方程kx-b=0的解是( )
A.(1,0) B.(0,-1) C.x=1 D.x=-1
6.已知方程2x+1=-x+4的解是x=1,则直线y=2x+1与y=-x+4的交点是( )
A.(1,0) B.(1,3) C.(-1,-1) D.(-1,5)
7.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可得关于x的方程kx+b=0的解为( )
A.x=-1 B.x=2 C.x=0 D.x=3
巩固提高全练
8.某快递公司每天上午7:00—8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的有( )
①15分钟后,甲仓库内快件数量为180件;②乙仓库每分钟派送快件的数量为4件;
③8:00时,甲仓库内快件数量为400件;④7:20时,两仓库快件数量相同.
A.1个 B.2个 C.3个 D.4个
9.某校为表彰在“创文明城,赞泰安城”书画比赛中表现优秀的同学,决定购买水彩盒或钢笔作为奖品.已知1个水彩盒28元,1支钢笔30元.
(1)恰逢“十一”,商店举行“优惠促销”活动,具体办法如下:水彩盒“九折”优惠;购买钢笔10支以上,超出10支的部分“八折”优惠,若买x个水彩盒需要y1元,买x支钢笔需要y2元,求y1,y2关于x的函数关系式;
(2)当购买数量为多少时,购买两种奖品的费用相同?
(3)当购买数量为80时,购买两种奖品的费用差距是多少?
10.我市全民健身中心面向学生推出假期游泳优惠活动,活动方案如下:
方案一:购买一张学生卡,每次游泳费用按六折优惠;
方案二:不购买学生卡,每次游泳费用按八折优惠.
设某学生假期游泳x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.
(1)求y1关于x的函数关系式,并直接写出单独购买一张学生卡的费用和购买学生卡后每次游泳的费用;
(2)求打折前的每次游泳费用和k2的值;
(3)八年级学生小明计划假期前往全民健身中心游泳8次,选择哪种方案所需费用更少?说明理由.
11.数形结合是解决数学问题常用的思想方法.如图所示,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
12.甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A.乙队率先到达终点 B.甲队比乙队多走了126米
C.在47.8秒时,两队所走路程相等 D.从出发到13.7秒的时间段内,乙队的速度慢
13.如图所示,在平面直角坐标系中,直线与直线y=-2x+2相交于点P,并分别与x轴相交于点A、B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图象中直线y=-2x+2在直线上方的部分描黑加粗,并写出此时自变量x的取值范围.
14.已知A、B两地之间有一条长240千米的公路.甲车从A地出发匀速开往B地,甲车出发两小时后,乙车从B地出发匀速开往A地,两车同时到达各自的目的地.两车行驶的路程之和y(千米)与甲车行驶的时间x(时)之间的函数关系如图所示.
(1)甲车的速度为________千米/时,a的值为_________;
(2)求乙车出发后,y与x之间的函数关系式;
(3)当甲、乙两车相距100千米时,求甲车行驶的时间.
15. “低碳生活,绿色出行”是一种环保,健康的生活方式,小丽从甲地出发沿一条笔直的公路骑行前往乙地,她与乙地之间的距离y(km)与出发时间t(h)之间的函数关系如图①中线段AB所示.在小丽出发的同时,小明从乙地沿同一条公路骑车匀速前往甲地,两人之间的距离x(km)与出发时间t(h)之间的函数关系如图②中折线段CD—DE—EF所示,
(1)小丽和小明骑车的速度各是多少?
(2)求点E的坐标,并解释点E的实际意义,
参考答案
1.C 2.C 3.44
4.解析 (1)设y关于x的函数解析式是y=kx+b(k≠0),
把(0,6),(15,3)分别代入解析式得b=6,15k+b=3,∴,
即y关于x的函数解析式是.
(2)当h=0时,,解得x=20,
当y=0时,,解得x=30,
∵20<30,∴甲先到达一楼地面.
5.C 6.B 7.A 8.C
9.解析 (1)y1=28×90%x,即y1=25.2x,
当0<x≤10时,y2=30x,
当x>10时,y2=30×10+30×80%(x-10),即y2=24x+60.
(2)当0<x≤10时,25.2x=30x,方程无解;
当x>10时,25.2x=24x+60,解得x=50.
答:当购买数量为50时,购买两种奖品的费用相同.
(3)当x=80时,y1=25.2×80=2016,y2=24×80+60=1980,
2016-1980=36(元).
答:当购买数量为80时,购买两种奖品费用的差距为36元.
10.解析 (1)∵y1=k1x+b的函数图象过点(0,30),(10,180),
∴b=30,10k1+b=180,解得k1=15,y1=15x+30.
单独购买一张学生卡的费用为30元.
购买一张学生卡后每次游泳费用为15元.
(2)由题意可得,打折前的每次游泳费用为15÷0.6=25(元),则k2=25×0.8=20.
(3)选择方案一所需费用更少.理由如下:
由题意可知,y1=15x+30,y2=20x.
当游泳8次时,y1=15×8+30=150,y2=20×8=160,
∵150<160,∴选择方案一所需费用更少.
11.A 12.C
13.解析 (1)令=-2x+2,解得x=2,
将x=2代入y=-2x+2,得y=2,∴P(2,-2).
(2)直线中,令y=0,则=0,解得x=-2,
直线y=-2x+2中,令y=0,则-2x+2=0,解得x=1,
∴A(-2,0),B(1,0),∴AB=3,
∴S△PAB==×3×2=3.
(3)如图所示:
自变量x的取值范围是x<2.
14.解析 (1)由题意可知,甲车的速度为80÷2=40(千米/时),a=240×2=480.
故答案为40;480.
(2)设y与x之间的函数关系式为y=kx+b(k≠0),
由题图可知,函数图象经过(2,80),(6,480),
∴2k+b=80,6k+b=480,解得k=100,b=-120,
∴y与x之间的函数关系式为y=100x-120(2≤x≤6).
(3)两车相遇前:80+100(x-2)=240-100,解得;
两车相遇后:80+100(x-2)=240+100,解得.
答:当甲、乙两车相距100千米时,甲车行驶的时间是小时或小时.
15.解析(1)由题意可得,小丽骑车的速度==16(km/h).
设小明骑车的速度为akm/h,
由题意得1×(16+a)=36,∴a=20.
答:小明骑车的速度为20km/h,小丽骑车的速度为16km/h.
(2)由题中图象可得,点E表示小明到了甲地,此时小丽没到乙地,
∴点E的横坐标=,点E的纵坐标=,
∴E.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 一次函数
5 一次函数的应用
知识能力全练
知识点一 利用一次函数解决实际问题
1.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内剩余油量Q(升)与行驶时间t(时)的关系式为( )
A.Q=5t B.Q=5t+40 C.Q=40-5t(0≤t≤8) D.以上答案都不对
2.如图所示,0A,BA分别表示甲、乙两名运动员运动的路程s(米)与时间t(秒)间的关系,则甲的速度比乙的速度每秒快( )
A.2.5米 B.2米 C.1.5米 D.1米
3.我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费方式,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水20吨,则应交水费_________元.
4.如图①,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系,乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图②所示.
(1)求y关于x的函数解析式;
(2)请通过计算说明甲、乙两人谁先到达一楼地面.
知识点二 一元一次方程kx+b=0(k≠0)与一次函数y=kx+b(k≠0)的关系
5.一次函数y=kx-b的图象如图所示,则关于x的方程kx-b=0的解是( )
A.(1,0) B.(0,-1) C.x=1 D.x=-1
6.已知方程2x+1=-x+4的解是x=1,则直线y=2x+1与y=-x+4的交点是( )
A.(1,0) B.(1,3) C.(-1,-1) D.(-1,5)
7.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可得关于x的方程kx+b=0的解为( )
A.x=-1 B.x=2 C.x=0 D.x=3
巩固提高全练
8.某快递公司每天上午7:00—8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的有( )
①15分钟后,甲仓库内快件数量为180件;②乙仓库每分钟派送快件的数量为4件;
③8:00时,甲仓库内快件数量为400件;④7:20时,两仓库快件数量相同.
A.1个 B.2个 C.3个 D.4个
9.某校为表彰在“创文明城,赞泰安城”书画比赛中表现优秀的同学,决定购买水彩盒或钢笔作为奖品.已知1个水彩盒28元,1支钢笔30元.
(1)恰逢“十一”,商店举行“优惠促销”活动,具体办法如下:水彩盒“九折”优惠;购买钢笔10支以上,超出10支的部分“八折”优惠,若买x个水彩盒需要y1元,买x支钢笔需要y2元,求y1,y2关于x的函数关系式;
(2)当购买数量为多少时,购买两种奖品的费用相同?
(3)当购买数量为80时,购买两种奖品的费用差距是多少?
10.我市全民健身中心面向学生推出假期游泳优惠活动,活动方案如下:
方案一:购买一张学生卡,每次游泳费用按六折优惠;
方案二:不购买学生卡,每次游泳费用按八折优惠.
设某学生假期游泳x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.
(1)求y1关于x的函数关系式,并直接写出单独购买一张学生卡的费用和购买学生卡后每次游泳的费用;
(2)求打折前的每次游泳费用和k2的值;
(3)八年级学生小明计划假期前往全民健身中心游泳8次,选择哪种方案所需费用更少?说明理由.
11.数形结合是解决数学问题常用的思想方法.如图所示,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
12.甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A.乙队率先到达终点 B.甲队比乙队多走了126米
C.在47.8秒时,两队所走路程相等 D.从出发到13.7秒的时间段内,乙队的速度慢
13.如图所示,在平面直角坐标系中,直线与直线y=-2x+2相交于点P,并分别与x轴相交于点A、B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图象中直线y=-2x+2在直线上方的部分描黑加粗,并写出此时自变量x的取值范围.
14.已知A、B两地之间有一条长240千米的公路.甲车从A地出发匀速开往B地,甲车出发两小时后,乙车从B地出发匀速开往A地,两车同时到达各自的目的地.两车行驶的路程之和y(千米)与甲车行驶的时间x(时)之间的函数关系如图所示.
(1)甲车的速度为________千米/时,a的值为_________;
(2)求乙车出发后,y与x之间的函数关系式;
(3)当甲、乙两车相距100千米时,求甲车行驶的时间.
15. “低碳生活,绿色出行”是一种环保,健康的生活方式,小丽从甲地出发沿一条笔直的公路骑行前往乙地,她与乙地之间的距离y(km)与出发时间t(h)之间的函数关系如图①中线段AB所示.在小丽出发的同时,小明从乙地沿同一条公路骑车匀速前往甲地,两人之间的距离x(km)与出发时间t(h)之间的函数关系如图②中折线段CD—DE—EF所示,
(1)小丽和小明骑车的速度各是多少?
(2)求点E的坐标,并解释点E的实际意义,
参考答案
1.C 2.C 3.44
4.解析 (1)设y关于x的函数解析式是y=kx+b(k≠0),
把(0,6),(15,3)分别代入解析式得b=6,15k+b=3,∴,
即y关于x的函数解析式是.
(2)当h=0时,,解得x=20,
当y=0时,,解得x=30,
∵20<30,∴甲先到达一楼地面.
5.C 6.B 7.A 8.C
9.解析 (1)y1=28×90%x,即y1=25.2x,
当0<x≤10时,y2=30x,
当x>10时,y2=30×10+30×80%(x-10),即y2=24x+60.
(2)当0<x≤10时,25.2x=30x,方程无解;
当x>10时,25.2x=24x+60,解得x=50.
答:当购买数量为50时,购买两种奖品的费用相同.
(3)当x=80时,y1=25.2×80=2016,y2=24×80+60=1980,
2016-1980=36(元).
答:当购买数量为80时,购买两种奖品费用的差距为36元.
10.解析 (1)∵y1=k1x+b的函数图象过点(0,30),(10,180),
∴b=30,10k1+b=180,解得k1=15,y1=15x+30.
单独购买一张学生卡的费用为30元.
购买一张学生卡后每次游泳费用为15元.
(2)由题意可得,打折前的每次游泳费用为15÷0.6=25(元),则k2=25×0.8=20.
(3)选择方案一所需费用更少.理由如下:
由题意可知,y1=15x+30,y2=20x.
当游泳8次时,y1=15×8+30=150,y2=20×8=160,
∵150<160,∴选择方案一所需费用更少.
11.A 12.C
13.解析 (1)令=-2x+2,解得x=2,
将x=2代入y=-2x+2,得y=2,∴P(2,-2).
(2)直线中,令y=0,则=0,解得x=-2,
直线y=-2x+2中,令y=0,则-2x+2=0,解得x=1,
∴A(-2,0),B(1,0),∴AB=3,
∴S△PAB==×3×2=3.
(3)如图所示:
自变量x的取值范围是x<2.
14.解析 (1)由题意可知,甲车的速度为80÷2=40(千米/时),a=240×2=480.
故答案为40;480.
(2)设y与x之间的函数关系式为y=kx+b(k≠0),
由题图可知,函数图象经过(2,80),(6,480),
∴2k+b=80,6k+b=480,解得k=100,b=-120,
∴y与x之间的函数关系式为y=100x-120(2≤x≤6).
(3)两车相遇前:80+100(x-2)=240-100,解得;
两车相遇后:80+100(x-2)=240+100,解得.
答:当甲、乙两车相距100千米时,甲车行驶的时间是小时或小时.
15.解析(1)由题意可得,小丽骑车的速度==16(km/h).
设小明骑车的速度为akm/h,
由题意得1×(16+a)=36,∴a=20.
答:小明骑车的速度为20km/h,小丽骑车的速度为16km/h.
(2)由题中图象可得,点E表示小明到了甲地,此时小丽没到乙地,
∴点E的横坐标=,点E的纵坐标=,
∴E.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
