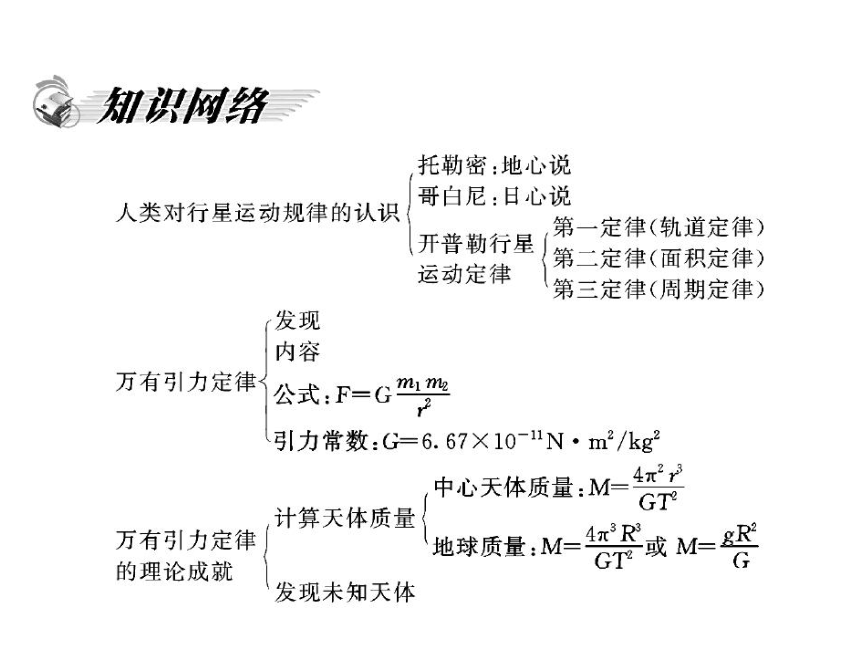
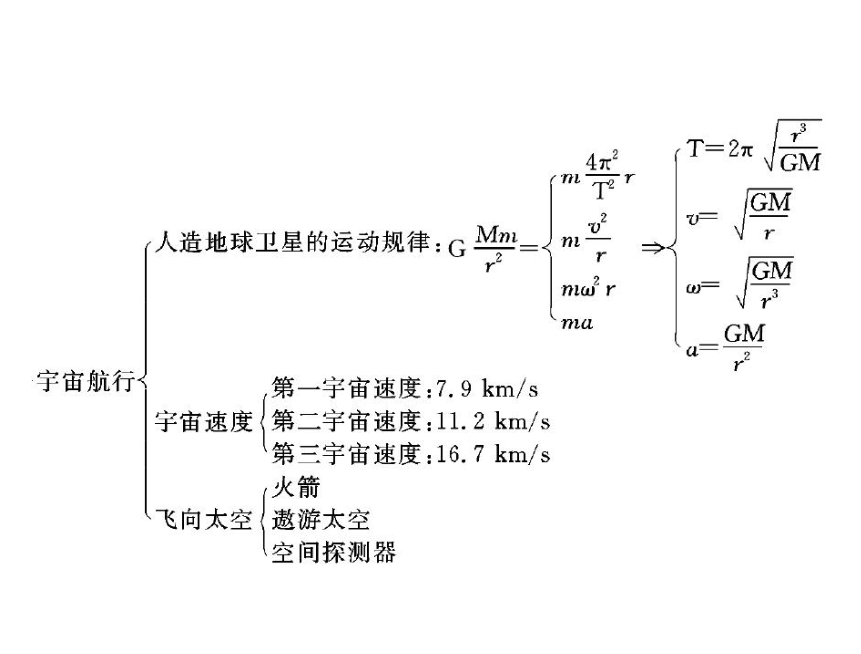
2012高一物理课件:第三章 章末整合 (粤教版必修2)
文档属性
| 名称 | 2012高一物理课件:第三章 章末整合 (粤教版必修2) |

|
|
| 格式 | zip | ||
| 文件大小 | 406.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-08-28 00:00:00 | ||
图片预览



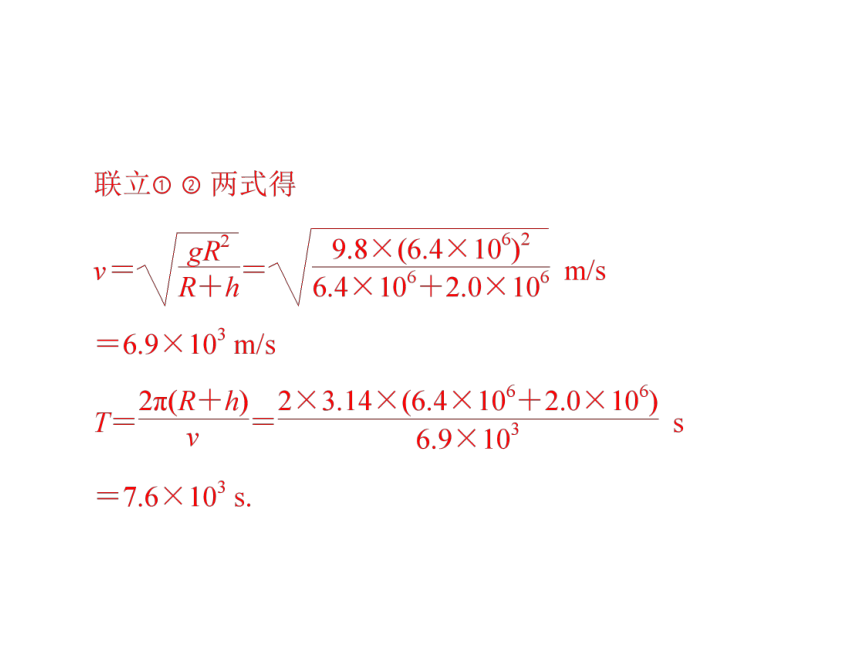

文档简介
(共19张PPT)
专题一 万有引力定律的综合应用
【例1】已知地球半径 R=6.4×106 m,地面附近的重力加
速度 g 取 9.8 m/s2,计算在距离地面高 h=2.0×106 m 的圆形轨
道上的卫星做匀速圆周运动的线速度 v 和周期 T.
专题二
天体运动的追及与相遇问题
天体运动的追及与相遇问题的本质是天体的变轨运行问
题.
要使低轨天体追上高轨天体,必须使低轨天体加速,通过
增大速度 v →增大做圆周运动所需的向心力 F向→F向>F引时,
做离心运动→增大轨道半径 r →升到高轨道运行的变速、变轨
过程而完成追及“任务”.
【例2】关于航天飞机与空间站对接问题,下列说法正确
的是(
)
A.先让航天飞机与空间站在同一轨道上,然后让航天飞
机加速,即可实现对接
B.先让航天飞机与空间站在同一轨道上,然后让航天飞
机减速,即可实现对接
C.先让航天飞机进入较低的轨道,然后再对其进行加速,
即可实现对接
D.先让航天飞机进入较高的轨道,然后再对其进行加速,
即可实现对接
解析:要使航天飞机与宇宙空间站成功“对接”,必须让
航天飞机在较低轨道上加速.
答案:C
1.(双选,2011 年广东卷)已知地球质量为 M,半径为 R,
自转周期为 T,地球同步卫星质量为 m,引力常量为 G.有关同
步卫星,下列表述正确的是(
)
A.卫星距离地面的高度为
B.卫星的运行速度小于第一宇宙速度
D.卫星运行的向心加速度小于地球表面的重力加速度
C.卫星运行时受到的向心力大小为
答案:BD
2.(2011 年全国卷)我国“嫦娥一号”探月卫星发射后,先
在“24 小时轨道”上绕地球运行(即绕地球一圈需要 24 小时);
然后,经过两次变轨依次到达“48 小时轨道”和“72 小时轨
道”;最后奔向月球.如果按圆形轨道计算,并忽略卫星质量
的变化,则在每次变轨完成后与变轨前相比(
)
D
A.卫星动能增大,引力势能减小
B.卫星动能增大,引力势能增大
C.卫星动能减小,引力势能减小
D.卫星动能减小,引力势能增大
解析:周期变长,表明轨道半径变大,速度减小,动能减
小,引力做负功故引力势能增大.
3.(双选,2011 年天津卷)质量为 m 的探月航天器在接近月
球表面的轨道上飞行,其运动视为匀速圆周运动.已知月球质
量为 M,月球半径为 R,月球表面重力加速度为 g,引力常量
)
为 G,不考虑月球自转的影响,则航天器的(
AC
4.(双选,2011 年山东卷)甲、乙为两颗地球卫星,其中甲
为地球同步卫星,乙的运行高度低于甲的运行高度,两卫星轨
)
道均可视为圆轨道.以下判断正确的是(
A.甲的周期大于乙的周期
B.乙的速度大于第一宇宙速度
C.甲的加速度小于乙的加速度
D.甲在运行时能经过北极的正上方
答案:AC
5.(2011 年北京卷)由于通信和广播等方面的需要,许多国
)
A
家发射了地球同步轨道卫星,这些卫星的(
A.质量可以不同
B.轨道半径可以不同
C.轨道平面可以不同
D.速率可以不同
6.(2010 年全国卷Ⅰ)如图 3-1 所示,质量分别为 m 和 M
的两个星球 A 和 B 在引力作用下都绕 O 点做匀速圆周运动,星
球 A 和 B 两者中心之间距离为 L.已知 A、B 的中心和 O 三点始
终共线,A 和 B 分别在 O 的两侧.引力常量为 G.
图 3-1
(1)求两星球做圆周运动的周期;
(2)在地月系统中,若忽略其他星球的影响,可以将月球和
地球看成上述星球 A 和 B,月球绕其轨道中心运行的周期记为
T1.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,
这样算得的运行周期为 T2. 已知地球和月球的质量分别为
5.98×1024 kg 和 7.35×1022 kg.求 T2 与 T1 两者平方之比.(结果
保留两位小数)
解:(1)A 和B 绕O 做匀速圆周运动,它们之间的万有引力
提供向心力,则A 和B 的向心力相等,且A 和B 与O 始终共
线,说明A 和B 有相同的角速度和周期.因此有
专题一 万有引力定律的综合应用
【例1】已知地球半径 R=6.4×106 m,地面附近的重力加
速度 g 取 9.8 m/s2,计算在距离地面高 h=2.0×106 m 的圆形轨
道上的卫星做匀速圆周运动的线速度 v 和周期 T.
专题二
天体运动的追及与相遇问题
天体运动的追及与相遇问题的本质是天体的变轨运行问
题.
要使低轨天体追上高轨天体,必须使低轨天体加速,通过
增大速度 v →增大做圆周运动所需的向心力 F向→F向>F引时,
做离心运动→增大轨道半径 r →升到高轨道运行的变速、变轨
过程而完成追及“任务”.
【例2】关于航天飞机与空间站对接问题,下列说法正确
的是(
)
A.先让航天飞机与空间站在同一轨道上,然后让航天飞
机加速,即可实现对接
B.先让航天飞机与空间站在同一轨道上,然后让航天飞
机减速,即可实现对接
C.先让航天飞机进入较低的轨道,然后再对其进行加速,
即可实现对接
D.先让航天飞机进入较高的轨道,然后再对其进行加速,
即可实现对接
解析:要使航天飞机与宇宙空间站成功“对接”,必须让
航天飞机在较低轨道上加速.
答案:C
1.(双选,2011 年广东卷)已知地球质量为 M,半径为 R,
自转周期为 T,地球同步卫星质量为 m,引力常量为 G.有关同
步卫星,下列表述正确的是(
)
A.卫星距离地面的高度为
B.卫星的运行速度小于第一宇宙速度
D.卫星运行的向心加速度小于地球表面的重力加速度
C.卫星运行时受到的向心力大小为
答案:BD
2.(2011 年全国卷)我国“嫦娥一号”探月卫星发射后,先
在“24 小时轨道”上绕地球运行(即绕地球一圈需要 24 小时);
然后,经过两次变轨依次到达“48 小时轨道”和“72 小时轨
道”;最后奔向月球.如果按圆形轨道计算,并忽略卫星质量
的变化,则在每次变轨完成后与变轨前相比(
)
D
A.卫星动能增大,引力势能减小
B.卫星动能增大,引力势能增大
C.卫星动能减小,引力势能减小
D.卫星动能减小,引力势能增大
解析:周期变长,表明轨道半径变大,速度减小,动能减
小,引力做负功故引力势能增大.
3.(双选,2011 年天津卷)质量为 m 的探月航天器在接近月
球表面的轨道上飞行,其运动视为匀速圆周运动.已知月球质
量为 M,月球半径为 R,月球表面重力加速度为 g,引力常量
)
为 G,不考虑月球自转的影响,则航天器的(
AC
4.(双选,2011 年山东卷)甲、乙为两颗地球卫星,其中甲
为地球同步卫星,乙的运行高度低于甲的运行高度,两卫星轨
)
道均可视为圆轨道.以下判断正确的是(
A.甲的周期大于乙的周期
B.乙的速度大于第一宇宙速度
C.甲的加速度小于乙的加速度
D.甲在运行时能经过北极的正上方
答案:AC
5.(2011 年北京卷)由于通信和广播等方面的需要,许多国
)
A
家发射了地球同步轨道卫星,这些卫星的(
A.质量可以不同
B.轨道半径可以不同
C.轨道平面可以不同
D.速率可以不同
6.(2010 年全国卷Ⅰ)如图 3-1 所示,质量分别为 m 和 M
的两个星球 A 和 B 在引力作用下都绕 O 点做匀速圆周运动,星
球 A 和 B 两者中心之间距离为 L.已知 A、B 的中心和 O 三点始
终共线,A 和 B 分别在 O 的两侧.引力常量为 G.
图 3-1
(1)求两星球做圆周运动的周期;
(2)在地月系统中,若忽略其他星球的影响,可以将月球和
地球看成上述星球 A 和 B,月球绕其轨道中心运行的周期记为
T1.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,
这样算得的运行周期为 T2. 已知地球和月球的质量分别为
5.98×1024 kg 和 7.35×1022 kg.求 T2 与 T1 两者平方之比.(结果
保留两位小数)
解:(1)A 和B 绕O 做匀速圆周运动,它们之间的万有引力
提供向心力,则A 和B 的向心力相等,且A 和B 与O 始终共
线,说明A 和B 有相同的角速度和周期.因此有
同课章节目录
