2012高一物理课件:第二章 第二节 向心力(粤教版必修2)
文档属性
| 名称 | 2012高一物理课件:第二章 第二节 向心力(粤教版必修2) |  | |
| 格式 | zip | ||
| 文件大小 | 493.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-08-28 16:23:07 | ||
图片预览








文档简介
(共31张PPT)
第二节 向心力
为_________,将ω= 代入得_________.
F=mω2r
一、向心力
1.做匀速圆周运动的物体受到的合外力不为零,总是沿半
径指向______,这个力叫做向心力.
圆心
垂直
2.向心力的方向:沿半径指向圆心,和质点运动方向_____.
向心力不改变速度的_____,只改变速度的_____.
方向
3.向心力的大小:物体做匀速圆周运动时所受向心力大小
v
r
大小
v2
r
F=m
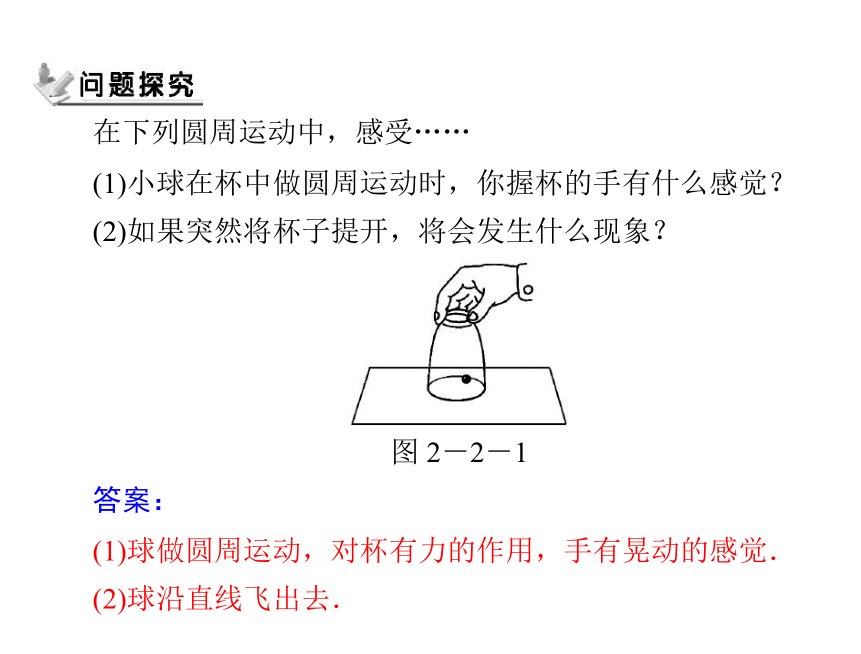
在下列圆周运动中,感受……
(1)小球在杯中做圆周运动时,你握杯的手有什么感觉?
(2)如果突然将杯子提开,将会发生什么现象?
图 2-2-1
答案:
(1)球做圆周运动,对杯有力的作用,手有晃动的感觉.
(2)球沿直线飞出去.
二、向心加速度
1.根据牛顿第二定律 F=ma,结合向心力大小公式得,向
心加速度大小为_________或_______.
a=ω2r
a=
v2
r
2.向心加速度的方向:沿半径指向圆心,和质点运动方向
_______.
垂直
三、生活中的向心力
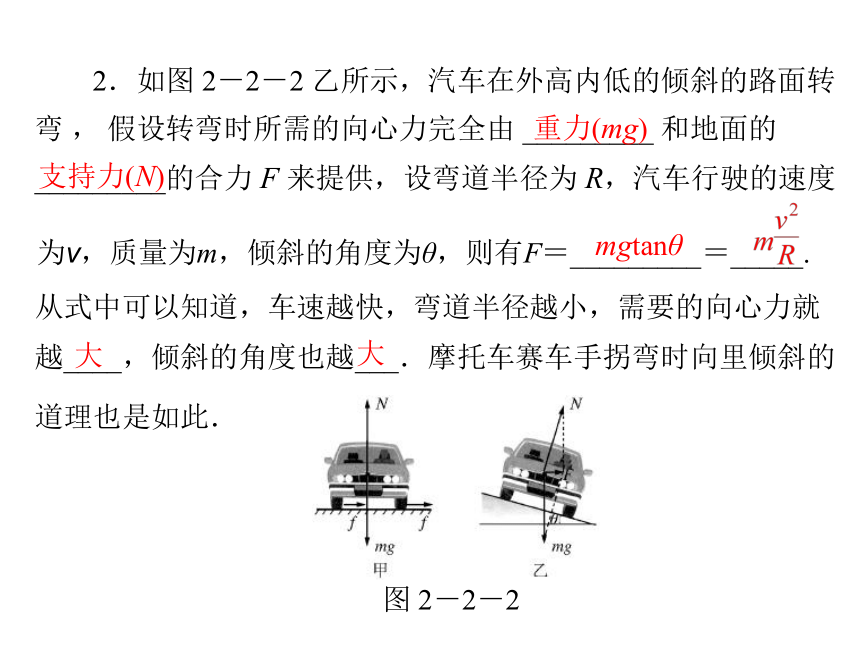
1.如图 2-2-2 甲所示,汽车在水平的公路上转弯时靠车
轮与路面间的__________来提供向心力,如果转弯时汽车速度
过快,则这个_________不足以提供汽车所需的向心力,汽车就
容易滑出路面.
静摩擦力
静摩擦力
2.如图 2-2-2 乙所示,汽车在外高内低的倾斜的路面转
弯 , 假设转弯时所需的向心力完全由 _________ 和地面的
_________的合力 F 来提供,设弯道半径为 R,汽车行驶的速度
从式中可以知道,车速越快,弯道半径越小,需要的向心力就
越____,倾斜的角度也越___.摩托车赛车手拐弯时向里倾斜的
道理也是如此.
重力(mg)
支持力(N)
mgtanθ
图 2-2-2
为v,质量为m,倾斜的角度为θ,则有F=_________=_____.
大
大
要点1
向心力的理解
1. 向心力公式:
2.向心力的性质
(1)向心力是效果力.
向心力因其方向时刻指向圆心而得名,故它为效果力.向
心力的作用效果是只改变速度的方向而不改变速度的大小.它
不是具有特定性质的某种力,任何性质的力都可以作为向心力,
受力分析时不分析向心力.
(2)向心力是变力.
向心力的方向指向圆心,与线速度方向垂直,方向时刻在
改变,故向心力是变力.
3. 向心力的来源
(1)在匀速圆周运动中,合外力一定是向心力;非匀速圆周
运动中,合外力沿半径方向的分力提供向心力.
(2)向心力是按力的作用效果来命名的,充当向心力的力可
以是重力、弹力和摩擦力等各种力,也可以是各力的合力或某
力的分力.
4.向心力与质量、角速度、线速度和半径的关系
(1)当质量和角速度一定时,向心力与半径成正比.
(2)当质量和线速度一定时,向心力与半径成反比.
(3)当质量和半径一定时,向心力与角速度(或线速度)的二
次方成正比.
(4)当角速度(或线速度)和半径一定时,向心力与质量成正
比.
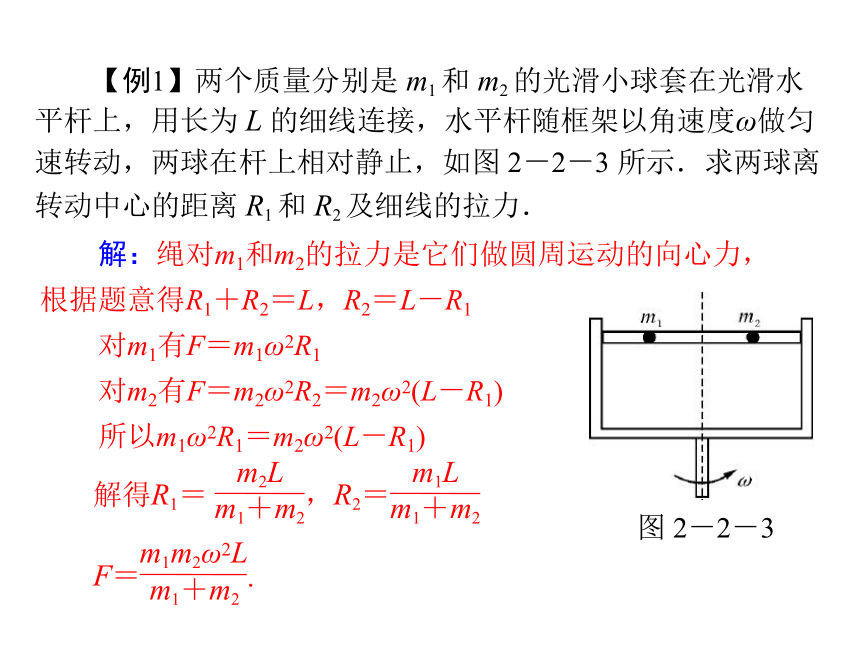
【例1】两个质量分别是 m1 和 m2 的光滑小球套在光滑水
平杆上,用长为 L 的细线连接,水平杆随框架以角速度ω做匀
速转动,两球在杆上相对静止,如图 2-2-3 所示.求两球离
转动中心的距离 R1 和 R2 及细线的拉力.
图 2-2-3
解得R1=
,R2=
m2L
m1+m2
m1L
m1+m2
F=
m1m2ω2L
m1+m2
.
解:绳对m1和m2的拉力是它们做圆周运动的向心力,根据题意得R1+R2=L,R2=L-R1
对m1有F=m1ω2R1
对m2有F=m2ω2R2=m2ω2(L-R1)
所以m1ω2R1=m2ω2(L-R1)
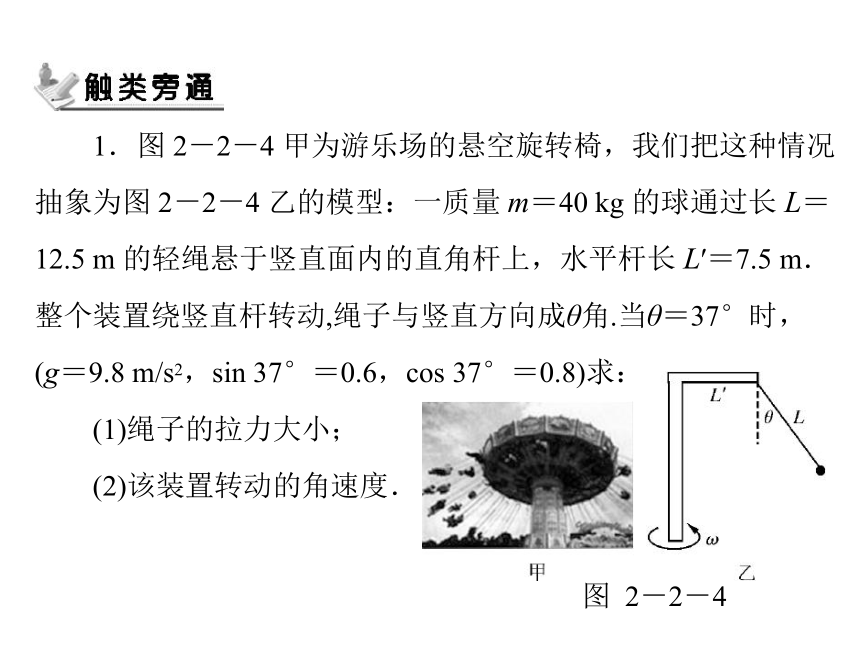
1.图 2-2-4 甲为游乐场的悬空旋转椅,我们把这种情况
抽象为图 2-2-4 乙的模型:一质量 m=40 kg 的球通过长 L=
12.5 m 的轻绳悬于竖直面内的直角杆上,水平杆长 L′=7.5 m.
整个装置绕竖直杆转动,绳子与竖直方向成θ角.当θ=37°时,
(g=9.8 m/s2,sin 37°=0.6,cos 37°=0.8)求:
(1)绳子的拉力大小;
(2)该装置转动的角速度.
图 2-2-4
解:(1)对球受力分析如图8 所示,则
F拉=
mg
cos 37°
代入数据得 F拉=490 N
(2)小球做圆周运动的向心力由绳拉力和重力
的合力提供,有 mgtan 37°=mω2(Lsin 37°+L′)
解得ω=
代入数据得ω=0.7 rad/s.
图8
要点2
向心加速度的理解
1.定义:做匀速圆周运动的物体具有沿半径指向圆心的加
速度,叫做向心加速度.
2.方向:时刻与物体的速度方向垂直且指向圆心.
4.向心加速度与角速度、线速度和半径的关系
(1)当线速度大小一定时,向心加速度与轨道半径成反比.
(2)当角速度一定时,向心加速度与轨道半径成正比.
(3)当半径一定时,向心加速度与角速度的平方成正比,也
与线速度的平方成正比.
5.实质:向心加速度是描述线速度方向改变快慢的物理量,
其方向时刻发生变化,且总是沿着轨迹半径指向圆心的方向,
所以匀速圆周运动是变加速运动.
【例2】如图 2-2-5 所示为一皮带传动装置,传动时不
打滑,O1 轮的半径为 O2 轮半径的两倍,O1 轮缘和 O2 轮缘上分
传动过程中 A、B、C 三点的向心加速度分别为 aA、aB、aC,则
(
)
图 2-2-5
A.aA∶aB∶aC=1∶2∶1
B.aA∶aB∶aC=1∶2∶4
C.aA∶aB∶aC=2∶1∶2
D.aA∶aB∶aC=1∶2∶2
答案:B
2.如图 2-2-6 所示的皮带传动装置中,轮 A 和轮 B 同
轴,A、B、C 分别是三个轮边缘的质点,且 RA=RC=2RB,则
)
A
三质点的向心加速度之比 aA∶aB∶aC 等于(
图 2-2-6
A.4∶2∶1 B.2∶1∶2
C.1∶2∶4 D.4∶1∶4
要点3
竖直平面内的圆周运动
1.图 2-2-7 甲、乙所示的是没有物体支撑的小球在竖直
平面做圆周运动过最高点的情况.
(1)能过最高点的临界条件:绳子或轨道对小球没有力的作用.
由 mg=m
v2
R
得 v临界= .
(2)能过最高点的条件:v≥ .当 v> 时,绳对球产生
拉力,轨道对球产生压力.
(3)不能过最高点的条件:v<v临界(实际上球还没到最高点
时就脱离了轨道).
图 2-2-7
2.如图 2-2-7 丙所示情形,小球与轻质杆相连.杆与绳
不同,它既能产生拉力,也能产生压力.
(1)能过最高点的临界条件:v临界=0,此时支持力 N=mg.
(2)当 0<v< 时,N 为支持力,有 0<N<mg,且 N 随 v
的增大而减小.
(3)当 v= 时,N=0.
(4)当 v> ,N 为拉力,有 N>0,N 随 v 的增大而增大.
【例3】一细杆与水桶相连,水桶中装有水,水桶与细杆
一起在竖直平面内做圆周运动,如图 2-2-8 所示.水的质量
m=0.5 kg,水的重心到转轴的距离 l=50 cm.(取 g=10 m/s2,不
计空气阻力)
图 2-2-8
(1)若在最高点水不流出来,求桶的最小速率;
(2)若在最高点水桶的速率 v=3 m/s,求水对桶底的压力.
解:(1)以水桶中的水为研究对象,在最高点恰好不流出来,
说明水的重力恰好提供其做圆周运动所需的向心力,此时桶的
速率最小.此时有
mg=m
v2
l
则所求的最小速率为
(2)在最高点,水具有向下的向心加速度,处于失重状态,
其向心加速度的大小由桶底对水的压力和水的重力决定.
3. 质量相等的小球 A、B 分别固定在轻杆的中点及端点,
当棒在光滑的水平面上绕 O 点匀速转动,如图 2-2-9 所示,
求 A、B 两球所受的拉力之比.
图 2-2-9
解:隔离A、B受力分析,如图9所示.由于A、B放在水平面上,故G=FN,又由A、B固定在同一根轻杆上,所以A、B的角速度相同,设角速度为ω,则由向心力公式可得
对A:FOA-FBA=mω2r
对B:FAB=mω22r
而FBA=FAB
联立以上式子得FOA∶FAB=3∶2.
图 9
要点4
生活中的圆周运动
1.汽车通过桥的最高点时,汽车所受的重力和桥对汽车的
支持力在一条直线上,它们的合力提供汽车做圆周运动所需的
向心力.
(1)凸形桥:如图 2-2-10 甲所示,当汽车通过桥的最高
点时,汽车对桥的压力小于汽车所受的重力.重力 G 和支持力
N 的合力为汽车做圆周运动的向心力,根据牛顿第二定律有 F向
压力.
图 2-2-10
(2)凹形桥:如图 2-2-10 乙所示,当汽车通过桥的最低
点时,汽车对桥的压力大于汽车所受的重力.重力 G 和支持力
N 的合力为汽车做圆周运动的向心力,根据牛顿第二定律有 F向
汽车过拱桥的分析方法对荡秋千过程中通过最低点和游乐
园里的过山车通过最低点、最高点的分析同样适用.
2.在航天器中所有和重力有关的仪器都无法使用.
(1)弹簧测力计无法测量物体的重力,但仍能测量拉力或压
力的大小.
(2)无法用天平测量物体的质量.
【例4】有一辆质量为 1.2 t 的小汽车驶上半径为 50 m 的圆
弧形拱桥,如图 2-2-11 所示.求:
(1)汽车到达桥顶的速度为 10 m/s 时对桥的压力有多大?
(2)汽车以多大的速度经过桥顶时恰好对桥没有压力作用
而腾空?
(3)设想拱桥的半径增大到与地球半径一样,那么汽车要在
这样的桥面上腾空,速度要多大?(重力加速度 g 取 10 m/s2,地
球半径 R 取 6.4×106 m)
图 2-2-11
4.在用高级沥青铺设的高速公路上,汽车的设计时速是
108 km/h.汽车在这种路面上行驶时,它的轮胎与地面的最大静
摩擦力等于车重的 0.6 倍.如果汽车在这种高速路的水平弯道
上拐弯,假设弯道的路面是水平的,其弯道的最小半径是多少?
如果高速路上设计了圆弧拱桥做立交桥,要使汽车能够安全通
过圆弧拱桥,这个圆弧拱桥的半径至少是多少?(取 g=10 m/s2)
【例 5】(双选)如图 2-2-12 所示,长为 L 的悬线固定在
L
2
拉到跟悬点在同一水平面上无初速度释放,小球运动到悬点正
)
图 2-2-12
下方时悬线碰到钉子,则小球的(
A.线速度突然增大
B.角速度突然减小
C.向心加速度突然增大
D.悬线拉力突然增大
O点,在O点正下方—处有一 钉子C,把悬线另一端的小球m
错因:认为线速度能够突然发生变化,错误地选择A.其实,
线速度变化需要时间,加速度变化不需要时间.
正解:球运动到悬点正下方时,悬线碰到钉子这一瞬间,
线速度不能发生突变,由于半径变小,角速度突然增大,悬线
拉力发生突变,突然增大.向心力发生突变,向心加速度也突
然增大.
答案:CD
第二节 向心力
为_________,将ω= 代入得_________.
F=mω2r
一、向心力
1.做匀速圆周运动的物体受到的合外力不为零,总是沿半
径指向______,这个力叫做向心力.
圆心
垂直
2.向心力的方向:沿半径指向圆心,和质点运动方向_____.
向心力不改变速度的_____,只改变速度的_____.
方向
3.向心力的大小:物体做匀速圆周运动时所受向心力大小
v
r
大小
v2
r
F=m
在下列圆周运动中,感受……
(1)小球在杯中做圆周运动时,你握杯的手有什么感觉?
(2)如果突然将杯子提开,将会发生什么现象?
图 2-2-1
答案:
(1)球做圆周运动,对杯有力的作用,手有晃动的感觉.
(2)球沿直线飞出去.
二、向心加速度
1.根据牛顿第二定律 F=ma,结合向心力大小公式得,向
心加速度大小为_________或_______.
a=ω2r
a=
v2
r
2.向心加速度的方向:沿半径指向圆心,和质点运动方向
_______.
垂直
三、生活中的向心力
1.如图 2-2-2 甲所示,汽车在水平的公路上转弯时靠车
轮与路面间的__________来提供向心力,如果转弯时汽车速度
过快,则这个_________不足以提供汽车所需的向心力,汽车就
容易滑出路面.
静摩擦力
静摩擦力
2.如图 2-2-2 乙所示,汽车在外高内低的倾斜的路面转
弯 , 假设转弯时所需的向心力完全由 _________ 和地面的
_________的合力 F 来提供,设弯道半径为 R,汽车行驶的速度
从式中可以知道,车速越快,弯道半径越小,需要的向心力就
越____,倾斜的角度也越___.摩托车赛车手拐弯时向里倾斜的
道理也是如此.
重力(mg)
支持力(N)
mgtanθ
图 2-2-2
为v,质量为m,倾斜的角度为θ,则有F=_________=_____.
大
大
要点1
向心力的理解
1. 向心力公式:
2.向心力的性质
(1)向心力是效果力.
向心力因其方向时刻指向圆心而得名,故它为效果力.向
心力的作用效果是只改变速度的方向而不改变速度的大小.它
不是具有特定性质的某种力,任何性质的力都可以作为向心力,
受力分析时不分析向心力.
(2)向心力是变力.
向心力的方向指向圆心,与线速度方向垂直,方向时刻在
改变,故向心力是变力.
3. 向心力的来源
(1)在匀速圆周运动中,合外力一定是向心力;非匀速圆周
运动中,合外力沿半径方向的分力提供向心力.
(2)向心力是按力的作用效果来命名的,充当向心力的力可
以是重力、弹力和摩擦力等各种力,也可以是各力的合力或某
力的分力.
4.向心力与质量、角速度、线速度和半径的关系
(1)当质量和角速度一定时,向心力与半径成正比.
(2)当质量和线速度一定时,向心力与半径成反比.
(3)当质量和半径一定时,向心力与角速度(或线速度)的二
次方成正比.
(4)当角速度(或线速度)和半径一定时,向心力与质量成正
比.
【例1】两个质量分别是 m1 和 m2 的光滑小球套在光滑水
平杆上,用长为 L 的细线连接,水平杆随框架以角速度ω做匀
速转动,两球在杆上相对静止,如图 2-2-3 所示.求两球离
转动中心的距离 R1 和 R2 及细线的拉力.
图 2-2-3
解得R1=
,R2=
m2L
m1+m2
m1L
m1+m2
F=
m1m2ω2L
m1+m2
.
解:绳对m1和m2的拉力是它们做圆周运动的向心力,根据题意得R1+R2=L,R2=L-R1
对m1有F=m1ω2R1
对m2有F=m2ω2R2=m2ω2(L-R1)
所以m1ω2R1=m2ω2(L-R1)
1.图 2-2-4 甲为游乐场的悬空旋转椅,我们把这种情况
抽象为图 2-2-4 乙的模型:一质量 m=40 kg 的球通过长 L=
12.5 m 的轻绳悬于竖直面内的直角杆上,水平杆长 L′=7.5 m.
整个装置绕竖直杆转动,绳子与竖直方向成θ角.当θ=37°时,
(g=9.8 m/s2,sin 37°=0.6,cos 37°=0.8)求:
(1)绳子的拉力大小;
(2)该装置转动的角速度.
图 2-2-4
解:(1)对球受力分析如图8 所示,则
F拉=
mg
cos 37°
代入数据得 F拉=490 N
(2)小球做圆周运动的向心力由绳拉力和重力
的合力提供,有 mgtan 37°=mω2(Lsin 37°+L′)
解得ω=
代入数据得ω=0.7 rad/s.
图8
要点2
向心加速度的理解
1.定义:做匀速圆周运动的物体具有沿半径指向圆心的加
速度,叫做向心加速度.
2.方向:时刻与物体的速度方向垂直且指向圆心.
4.向心加速度与角速度、线速度和半径的关系
(1)当线速度大小一定时,向心加速度与轨道半径成反比.
(2)当角速度一定时,向心加速度与轨道半径成正比.
(3)当半径一定时,向心加速度与角速度的平方成正比,也
与线速度的平方成正比.
5.实质:向心加速度是描述线速度方向改变快慢的物理量,
其方向时刻发生变化,且总是沿着轨迹半径指向圆心的方向,
所以匀速圆周运动是变加速运动.
【例2】如图 2-2-5 所示为一皮带传动装置,传动时不
打滑,O1 轮的半径为 O2 轮半径的两倍,O1 轮缘和 O2 轮缘上分
传动过程中 A、B、C 三点的向心加速度分别为 aA、aB、aC,则
(
)
图 2-2-5
A.aA∶aB∶aC=1∶2∶1
B.aA∶aB∶aC=1∶2∶4
C.aA∶aB∶aC=2∶1∶2
D.aA∶aB∶aC=1∶2∶2
答案:B
2.如图 2-2-6 所示的皮带传动装置中,轮 A 和轮 B 同
轴,A、B、C 分别是三个轮边缘的质点,且 RA=RC=2RB,则
)
A
三质点的向心加速度之比 aA∶aB∶aC 等于(
图 2-2-6
A.4∶2∶1 B.2∶1∶2
C.1∶2∶4 D.4∶1∶4
要点3
竖直平面内的圆周运动
1.图 2-2-7 甲、乙所示的是没有物体支撑的小球在竖直
平面做圆周运动过最高点的情况.
(1)能过最高点的临界条件:绳子或轨道对小球没有力的作用.
由 mg=m
v2
R
得 v临界= .
(2)能过最高点的条件:v≥ .当 v> 时,绳对球产生
拉力,轨道对球产生压力.
(3)不能过最高点的条件:v<v临界(实际上球还没到最高点
时就脱离了轨道).
图 2-2-7
2.如图 2-2-7 丙所示情形,小球与轻质杆相连.杆与绳
不同,它既能产生拉力,也能产生压力.
(1)能过最高点的临界条件:v临界=0,此时支持力 N=mg.
(2)当 0<v< 时,N 为支持力,有 0<N<mg,且 N 随 v
的增大而减小.
(3)当 v= 时,N=0.
(4)当 v> ,N 为拉力,有 N>0,N 随 v 的增大而增大.
【例3】一细杆与水桶相连,水桶中装有水,水桶与细杆
一起在竖直平面内做圆周运动,如图 2-2-8 所示.水的质量
m=0.5 kg,水的重心到转轴的距离 l=50 cm.(取 g=10 m/s2,不
计空气阻力)
图 2-2-8
(1)若在最高点水不流出来,求桶的最小速率;
(2)若在最高点水桶的速率 v=3 m/s,求水对桶底的压力.
解:(1)以水桶中的水为研究对象,在最高点恰好不流出来,
说明水的重力恰好提供其做圆周运动所需的向心力,此时桶的
速率最小.此时有
mg=m
v2
l
则所求的最小速率为
(2)在最高点,水具有向下的向心加速度,处于失重状态,
其向心加速度的大小由桶底对水的压力和水的重力决定.
3. 质量相等的小球 A、B 分别固定在轻杆的中点及端点,
当棒在光滑的水平面上绕 O 点匀速转动,如图 2-2-9 所示,
求 A、B 两球所受的拉力之比.
图 2-2-9
解:隔离A、B受力分析,如图9所示.由于A、B放在水平面上,故G=FN,又由A、B固定在同一根轻杆上,所以A、B的角速度相同,设角速度为ω,则由向心力公式可得
对A:FOA-FBA=mω2r
对B:FAB=mω22r
而FBA=FAB
联立以上式子得FOA∶FAB=3∶2.
图 9
要点4
生活中的圆周运动
1.汽车通过桥的最高点时,汽车所受的重力和桥对汽车的
支持力在一条直线上,它们的合力提供汽车做圆周运动所需的
向心力.
(1)凸形桥:如图 2-2-10 甲所示,当汽车通过桥的最高
点时,汽车对桥的压力小于汽车所受的重力.重力 G 和支持力
N 的合力为汽车做圆周运动的向心力,根据牛顿第二定律有 F向
压力.
图 2-2-10
(2)凹形桥:如图 2-2-10 乙所示,当汽车通过桥的最低
点时,汽车对桥的压力大于汽车所受的重力.重力 G 和支持力
N 的合力为汽车做圆周运动的向心力,根据牛顿第二定律有 F向
汽车过拱桥的分析方法对荡秋千过程中通过最低点和游乐
园里的过山车通过最低点、最高点的分析同样适用.
2.在航天器中所有和重力有关的仪器都无法使用.
(1)弹簧测力计无法测量物体的重力,但仍能测量拉力或压
力的大小.
(2)无法用天平测量物体的质量.
【例4】有一辆质量为 1.2 t 的小汽车驶上半径为 50 m 的圆
弧形拱桥,如图 2-2-11 所示.求:
(1)汽车到达桥顶的速度为 10 m/s 时对桥的压力有多大?
(2)汽车以多大的速度经过桥顶时恰好对桥没有压力作用
而腾空?
(3)设想拱桥的半径增大到与地球半径一样,那么汽车要在
这样的桥面上腾空,速度要多大?(重力加速度 g 取 10 m/s2,地
球半径 R 取 6.4×106 m)
图 2-2-11
4.在用高级沥青铺设的高速公路上,汽车的设计时速是
108 km/h.汽车在这种路面上行驶时,它的轮胎与地面的最大静
摩擦力等于车重的 0.6 倍.如果汽车在这种高速路的水平弯道
上拐弯,假设弯道的路面是水平的,其弯道的最小半径是多少?
如果高速路上设计了圆弧拱桥做立交桥,要使汽车能够安全通
过圆弧拱桥,这个圆弧拱桥的半径至少是多少?(取 g=10 m/s2)
【例 5】(双选)如图 2-2-12 所示,长为 L 的悬线固定在
L
2
拉到跟悬点在同一水平面上无初速度释放,小球运动到悬点正
)
图 2-2-12
下方时悬线碰到钉子,则小球的(
A.线速度突然增大
B.角速度突然减小
C.向心加速度突然增大
D.悬线拉力突然增大
O点,在O点正下方—处有一 钉子C,把悬线另一端的小球m
错因:认为线速度能够突然发生变化,错误地选择A.其实,
线速度变化需要时间,加速度变化不需要时间.
正解:球运动到悬点正下方时,悬线碰到钉子这一瞬间,
线速度不能发生突变,由于半径变小,角速度突然增大,悬线
拉力发生突变,突然增大.向心力发生突变,向心加速度也突
然增大.
答案:CD
同课章节目录
