双曲线的标准方程习题(Word含答案)
文档属性
| 名称 | 双曲线的标准方程习题(Word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 210.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 00:00:00 | ||
图片预览




文档简介
双曲线的方程及其性质
1.已知平面上定点F1、F2及动点M,命题甲:||MF1|-|MF2||=2a(a为非零常数),命题乙:M点轨迹是以F1、F2为焦点的双曲线,则甲是乙的( )
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既不充分也不必要条件
2.P是双曲线的右支上一点,M、N分别是圆(x + 5) 2 + y2 = 4和(x 5) 2 + y2 = 1上的点,则|PM| |PN|的最大值为( )
A.6 B.7 C.8 D.9
3.双曲线(a > 0,b > 0),F1,F2为焦点,弦AB过F1且在双曲线的一支上,若,则=_______.
4.F1、F2是双曲线的两个焦点,P在双曲线上且满足|PF1|·|PF2|=32,则∠F1PF2=____________.
5.曲线的离心率为2,则________.
6.已知双曲线,过其右焦点且垂直于实轴的直线与双曲线交于两点,为坐标原点.若,则双曲线的离心率为( )
A. B.
7.如图,在△ABC中,已知|AB|=,且三内角A、B、C满足.
试建立适当的坐标系,求定点C的轨迹方程.
8.求与双曲线有相同焦点且过点的双曲线方程.
9.焦点在x轴上的双曲线,它的两条渐近线的夹角为,焦距为12,求此双曲线的方程及离心率.
10.求经过点A,且一条渐近线的方程为3x-4y = 0的双曲线方程.
11.已知双曲线过P1()和P2()两点,求双曲线的标准方程.
12.已知椭圆C1的方程为,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,求双曲线C2的方程.
13.已知M(-2,0)、N(2,0),|PM|-|PN| = 4,则动点P的轨迹是( )
A.双曲线 B.双曲线左边一支
C.一条射线 D.双曲线右边一支
14.半径不等的两定圆O1、O2无公共点(O1、O2是两个不同的点),动圆O与
圆O1、O2都内切,则圆心O轨迹是( )
A.双曲线的一支
B.椭圆或圆
C.双曲线的一支或椭圆或圆
D.双曲线的一支或椭圆
15.设点P是双曲线右支上一动点,M,N分别是圆(x+4)2+y2 = 1
和(x-4)2+y2 = 1上的动点,则|PM|-|PN|的取值范围是( )
A.[4,8] B.[2,6]
C.[6,8] D.[8,12]
16.过双曲线的右支上一点P,分别向圆C1:(x+4)2+y2 = 4和圆
C2:(x-4)2+y2 = 1作切线,切点分别为M,N,则|PM|2-|PN|2的最小值为 .
17.双曲线(a>0,b>0),过焦点F1的弦AB(A、B在双曲线的同支上)长为m,另一焦点为F2,则△ABF2的周长是 .
18.过双曲线(b>0)左焦点F1的直线l与双曲线左支交于A,B两点,若|AF2|+|BF2|(F2是双曲线的右焦点)的最小值为14,则b的值是 .
19.已知双曲线x2-y2 = 1的左、右焦点分别是F1、F2,点P在双曲线上,且∠F1PF2 = 60°,则|PF1| |PF2| = .
20.若F1,F2是双曲线的两个焦点,P是双曲线上的点,且|PF1| |PF2| = 32,试求△F1PF2的面积.
21.若双曲线mx2+y2 = 1的离心率为,则m = .
22.若曲线C方程为Ax2+By2 = 1,且A =-2B≠0,则曲线C的离心率为 .
23.在平面直角坐标系xOy中,双曲线E:的左顶点为A,过双曲线E的右焦点F作与实轴垂直的直线交双曲线E于B,C两点,若△ABC为直角三角形,角A是直角,则双曲线E的离心率为 .
24.已知F1、F2为双曲线的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e = .
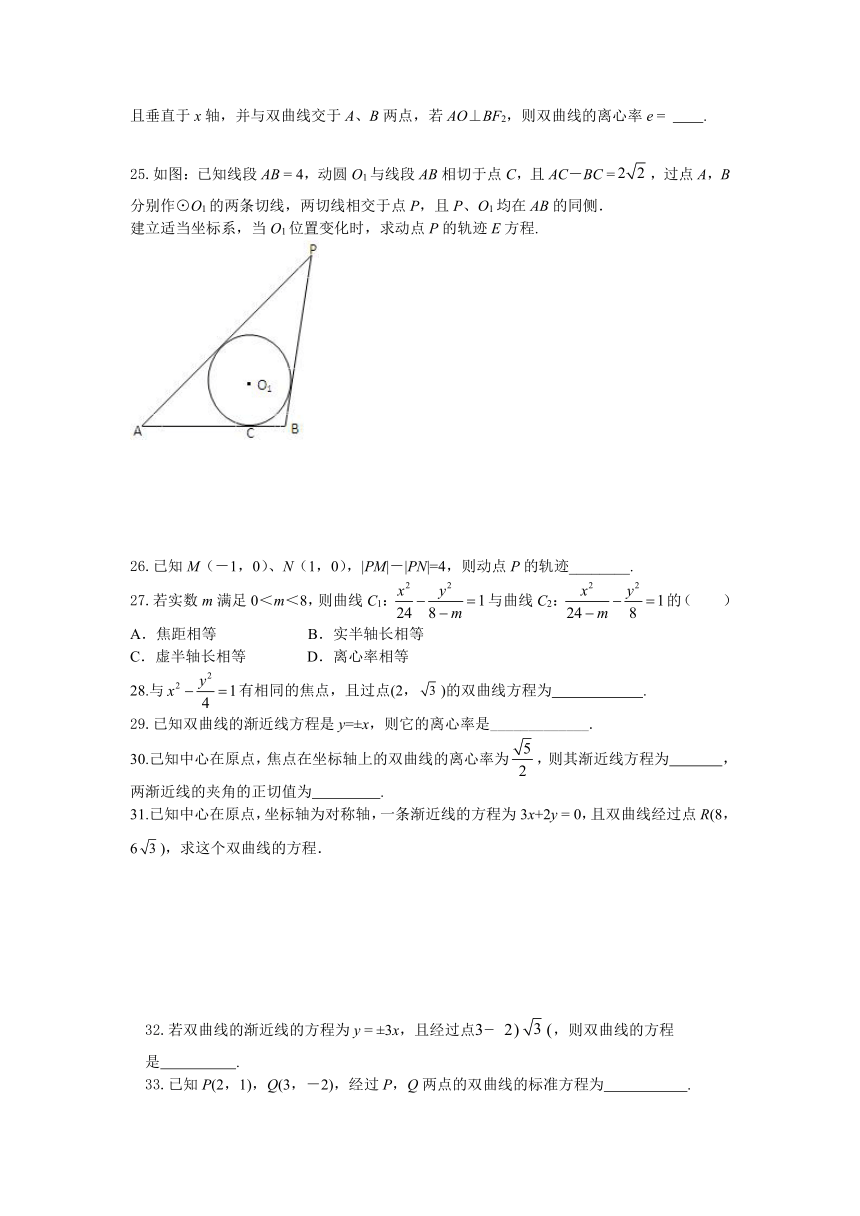
25.如图:已知线段AB = 4,动圆O1与线段AB相切于点C,且AC-BC =,过点A,B分别作⊙O1的两条切线,两切线相交于点P,且P、O1均在AB的同侧.
建立适当坐标系,当O1位置变化时,求动点P的轨迹E方程.
26.已知M(-1,0)、N(1,0),|PM|-|PN|=4,则动点P的轨迹________.
27.若实数m满足0<m<8,则曲线C1:与曲线C2:的( )
A.焦距相等 B.实半轴长相等
C.虚半轴长相等 D.离心率相等
28.与有相同的焦点,且过点(2,)的双曲线方程为 .
29.已知双曲线的渐近线方程是y=±x,则它的离心率是_____________.
30.己知中心在原点,焦点在坐标轴上的双曲线的离心率为,则其渐近线方程为 ,两渐近线的夹角的正切值为 .
31.已知中心在原点,坐标轴为对称轴,一条渐近线的方程为3x+2y = 0,且双曲线经过点R(8,6),求这个双曲线的方程.
32.若双曲线的渐近线的方程为y = ±3x,且经过点(2, 3),则双曲线的方程是 .
33.已知P(2,1),Q(3,-2),经过P,Q两点的双曲线的标准方程为 .
34.已知双曲线经过M(1,1),N(-2,5)两点,求双曲线的标准方程.
35.求以椭圆长轴上的顶点为焦点,椭圆焦点为顶点的双曲线方程.
36.已知双曲线的一个焦点与圆x2+y2-10x=0的圆心重合,且双曲线的离心率等于,则该双曲线的标准方程为________________.
1.B
2.D
3.4a
4.90°
5.
6.D
7.
8.
9.此双曲线的方程为,离心率为或者此双曲线的方程为,离心率为2.
10.
11.
12.
13.C.
详解:因为|MN| = 4,且|PM|-|PN| = 4,所以动点P的轨迹是一条射线.故选C.
14.D.
详解:两定圆O1、O2无公共点,它们的位置关系应是外离或内含:
设两定圆O1、O2的半径分别为r1,r2(r1>r2),圆O的半径为R,
当两圆外离时,|OO1| = R-r1,|OO2| = R-r2,∴|OO2|-|OO1| = r1-r2<|O1O2|,
∴圆心O的轨迹是双曲线的一支;
当两圆内含时,|OO1| = r1-R,|OO2| = R-r2,∴|OO2|+|OO1| = r1-r2>|O1O2|,
∴圆心O的轨迹是椭圆.
故选D.
15.A.
详解:由题意,圆(x+4)2+y2 = 1的圆心是(-4,0),圆(x-4)2+y2 = 1的圆心是(4,0),
双曲线的两个焦点坐标分别为(-4,0),(4,0),|PF1|-|PF2| = 2a = 6,
∴双曲线的焦点正好是两圆(x+4)2+y2 = 1和(x-4)2+y2 = 1的圆心,
∵两圆(x+4)2+y2 = 1和(x-4)2+y2 = 1的半径分别是r1 = 1,r2 = 1,
∴|PM|min = |PF1|-1,|PN|max = |PF2|+1,|PM|max = |PF1|+1,|PN|min = |PF2|-1,
∴(|PM|-|PN|)min =|PM|min-|PN|max=(|PF1|-1)-(|PF2|+1) = 6-2 = 4,
(|PM|-|PN|)max =|PM|max-|PN|min= (|PF1|+1)-(|PF2|-1) = 6+2 = 8,
∴|PM|-|PN|的取值范围是[4,8].故选A.
16.13.
详解:如图
圆C1:(x+4)2+y2 = 4的圆心为(-4,0),半径为r1 = 2,
圆C2:(x-4)2+y2 = 1的圆心为(4,0),半径为r2 = 1,
设双曲线的左右焦点坐标分别为F1(-4,0),F2(4,0),
连接PF1,PF2,F1M,F2N,可得
|PM|2-|PN|2 = (|PF1|2-r12)-(|PF2|2-r22)
= (|PF1|2-4)-(|PF2|2-1)
=|PF1|2-|PF2|2-3
= (|PF1|-|PF2|)(|PF1|+|PF2|)-3
= 2a(|PF1|+|PF2|)-3
= 2(|PF1|+|PF2|)-3≥2 2c-3 = 2 8-3 = 13.
当且仅当P为右顶点时,取得等号,即最小值13.
故答案为13.
17.4a+2m.
详解:如图,
∵|AF2|-|AF1| = 2a,|BF2|-|BF1| = 2a,
∴(|AF2|-|AF1|)+(|BF2|-|BF1|) = 4a,
又∵|AF1|+|BF1| = |AB| = m,
∴|AF2|+|BF2| = 4a+(|AF1|+|BF1|) = 4a+m.
∴△ABF2的周长等于|AF2|+|BF2|+|AB| = 4a+2m.
18..
详解:如图,
根据双曲线的标准方程(b>0),得a = 3,
由双曲线的定义可得|AF2|-|AF1| = 2a = 6 ①
|BF2|-|BF1| = 2a = 6 ②
①+②可得|AF2|+|BF2|-(|AF1|+|BF1|) = 12,
∵过双曲线的左焦点F1的直线交双曲线的左支于A,B两点,
∴|AF1|+|BF1| = |AB|,当|AB|是双曲线的通径时|AB|最小,通径长为.
∴|AF2|+|BF2|-(|AF1|+|BF1|)
= |AF2|+|BF2|-|AB| = 12.
∴|BF2|+|AF2| = |AB|+12≥+12 = 14,
∴b =.
19.4.
详解:在双曲线x2-y2 = 1中,a = b = 1,c =,
设P在右支上,则|PF1|-|PF2| = 2a = 2,
∵∠F1PF2 = 60°,
∴|F1F2|2 = |PF1|2+|PF2|2-2|PF1||PF2|cos60°
= (|PF1|-|PF2|)|2+2|PF1||PF2|-|PF1||PF2|,
即4c2 = 4a2+|PF1| |PF2|,
即|PF1| |PF2| = 4c2-4a2 = 4b2 = 4,
故答案为4.
20.16.
详解:根据双曲线的方程可知,a = 3,b = 4,c = 5,
则|F1F2| = 2c = 10,||PF1|-|PF2|| = 2a = 2×3 = 6,∴|PF1|2+|PF2|2-2|PF1||PF2| = 36,
∴|PF1|2+|PF2|2 = 100 = |F1F2|2,∴∠F1PF2 = 90°,
∴△F1PF2的面积为|PF1| |PF2| = 32×= 16.
也可用焦点三角形面积公式S△F1PF2=b2cot=16×1=16.
21.-1.
详解:双曲线mx2+y2 = 1即,
∴e2 ==1+ = 2,∴m =-1.
故答案为-1.
22.或.
详解:∵A =-2B ≠ 0,∴A,B符号相反,
①若A>0,则方程等价为,为双曲线,其中a2 =,b2 =,
则c2 ==-,则e2 == 3,即离心率e =,
②若A<0,则方程等价为,为双曲线,其中a2 =,b2 =-,
则c2 = =+,则e2 =,即离心率e = .
23.2.
详解:∵过双曲线的右焦点F作与实轴垂直的直线交双曲线E于B,C两点,∴设x = c,得,解之得y = ±,得B(c,)、C(c,-)
∵左顶点A(-a,0)与B、C构成直角三角形,
∴根据双曲线的对称性,得A到BC的距离等于BC长的一半,
可得c+a =,即c+a =,化简得c2-ac-2a2 = 0,
两边都除以a2,得e2-e-2 = 0,解之得e = 2(舍负),即双曲线E的离心率为2.
故答案为2.
24..
详解:由题意得:F1(-c,0),F2(c,0),A(-c,),B(-c,-),
∴直线AO的斜率k1 =,直线BF2的斜率k2 =,
∵AO⊥BF2,∴k1k2 =-1,即×= 1,∴b4 = 2a2c2,
又∵b2 = c2-a2,∴(c2-a2)2 = 2a2c2,解之得,又由于,
所以.
25..
详解:以AB为x轴,AB的垂直平分线为y轴,建立坐标系,令PA、PB与圆的切点分别为M、N.
∴|PM|=|PN|,|AM|=|AC|,|BC|=|BN|,
则|PA|-|PB| = |AC|-|BC| = ,
∴点P在以A、B为焦点双曲线的一支上,且2c = 4,2a =,
∴c = 2,a =,∴b =,
∴P点的轨迹E为.
26.不存在.
因为|MN|=2,且|PM|-|PN|=4>|MN|,所以动点P的轨迹不存在.
27.A.
详解:由于0<m<8,则0<8-m<8,16<24-m<24,
即曲线C1:表示焦点在x轴上的双曲线,
其中a2=24,b2=8-m,c2=32-m,
曲线C2:表示焦点在x轴上的双曲线,
其中a ’2=24-m,b’2=8,c’2=32-m,
即两个双曲线的焦距相等,故选:A.
28..
详解:设方程为,将点(2,)代入方程得λ = 1.
所以方程为.故答案为.
29.
详解:∵双曲线的渐近线方程是y=±x,
∴或,可得a=b,
∴离心率e=.
30.y = ±x或y = ±2x;.
详解:由题意可得e =,即为c =,由b2 = c2-a2 =a2,即a = 2b,
当焦点在x轴上时,渐近线方程为y = ±x,即为y = ±x;
当焦点在y轴上时,渐近线方程为y = ±x,即为y = ±2x;
当焦点在x轴上时,根据正切的二倍角公式,两渐近线的夹角的正切为;
同理,当焦点在y轴上时,由于夹角是锐角或直角,所以两渐近线的夹角的正切为.
31..
详解:因为双曲线的渐近线方程为3x+2y = 0,所以设曲线的标准方程为9x2-4y2 = λ,
因为双曲线过点R(8,6),所以9×64-4×108 = 144 = λ,
所以曲线的标准方程为9x2-4y2 = 144,即.
32..
详解:由题意可知,可设双曲线的方程是,
把点(2, 3)代入方程解得k = 1,
故所求的双曲线的方程是.
33..
详解:设所求双曲线方程为mx2+ny2 = 1(mn < 0),
∵P(2,1),Q(3,-2)两点在双曲线上,∴,
∴经过P,Q两点的双曲线的标准方程为.
34..
详解:设所求双曲线方程为mx2+ny2 = 1(mn < 0),
∵M(1,1),N(-2,5)两点在双曲线上,∴,
∴双曲线方程是,整理得.
35..
详解:椭圆的长轴顶点为(0,-2)和(0,2),
焦点为(0,-2)和(0,2),
∴双曲线的焦点坐标是(0,-2)和(0,2),顶点为(0,-2)和(0,2),
∴双曲线方程为.
36..
详解:圆x2+y2-10x=0化成标准方程得(x-5)2+y2=25,
∴圆的圆心坐标为(5,0),即双曲线的焦点坐标为F(5,0),
∵双曲线的离心率等于,
∴,
∴,
∴双曲线的标准方程为.
1.已知平面上定点F1、F2及动点M,命题甲:||MF1|-|MF2||=2a(a为非零常数),命题乙:M点轨迹是以F1、F2为焦点的双曲线,则甲是乙的( )
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既不充分也不必要条件
2.P是双曲线的右支上一点,M、N分别是圆(x + 5) 2 + y2 = 4和(x 5) 2 + y2 = 1上的点,则|PM| |PN|的最大值为( )
A.6 B.7 C.8 D.9
3.双曲线(a > 0,b > 0),F1,F2为焦点,弦AB过F1且在双曲线的一支上,若,则=_______.
4.F1、F2是双曲线的两个焦点,P在双曲线上且满足|PF1|·|PF2|=32,则∠F1PF2=____________.
5.曲线的离心率为2,则________.
6.已知双曲线,过其右焦点且垂直于实轴的直线与双曲线交于两点,为坐标原点.若,则双曲线的离心率为( )
A. B.
7.如图,在△ABC中,已知|AB|=,且三内角A、B、C满足.
试建立适当的坐标系,求定点C的轨迹方程.
8.求与双曲线有相同焦点且过点的双曲线方程.
9.焦点在x轴上的双曲线,它的两条渐近线的夹角为,焦距为12,求此双曲线的方程及离心率.
10.求经过点A,且一条渐近线的方程为3x-4y = 0的双曲线方程.
11.已知双曲线过P1()和P2()两点,求双曲线的标准方程.
12.已知椭圆C1的方程为,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,求双曲线C2的方程.
13.已知M(-2,0)、N(2,0),|PM|-|PN| = 4,则动点P的轨迹是( )
A.双曲线 B.双曲线左边一支
C.一条射线 D.双曲线右边一支
14.半径不等的两定圆O1、O2无公共点(O1、O2是两个不同的点),动圆O与
圆O1、O2都内切,则圆心O轨迹是( )
A.双曲线的一支
B.椭圆或圆
C.双曲线的一支或椭圆或圆
D.双曲线的一支或椭圆
15.设点P是双曲线右支上一动点,M,N分别是圆(x+4)2+y2 = 1
和(x-4)2+y2 = 1上的动点,则|PM|-|PN|的取值范围是( )
A.[4,8] B.[2,6]
C.[6,8] D.[8,12]
16.过双曲线的右支上一点P,分别向圆C1:(x+4)2+y2 = 4和圆
C2:(x-4)2+y2 = 1作切线,切点分别为M,N,则|PM|2-|PN|2的最小值为 .
17.双曲线(a>0,b>0),过焦点F1的弦AB(A、B在双曲线的同支上)长为m,另一焦点为F2,则△ABF2的周长是 .
18.过双曲线(b>0)左焦点F1的直线l与双曲线左支交于A,B两点,若|AF2|+|BF2|(F2是双曲线的右焦点)的最小值为14,则b的值是 .
19.已知双曲线x2-y2 = 1的左、右焦点分别是F1、F2,点P在双曲线上,且∠F1PF2 = 60°,则|PF1| |PF2| = .
20.若F1,F2是双曲线的两个焦点,P是双曲线上的点,且|PF1| |PF2| = 32,试求△F1PF2的面积.
21.若双曲线mx2+y2 = 1的离心率为,则m = .
22.若曲线C方程为Ax2+By2 = 1,且A =-2B≠0,则曲线C的离心率为 .
23.在平面直角坐标系xOy中,双曲线E:的左顶点为A,过双曲线E的右焦点F作与实轴垂直的直线交双曲线E于B,C两点,若△ABC为直角三角形,角A是直角,则双曲线E的离心率为 .
24.已知F1、F2为双曲线的两焦点,O是坐标原点,直线AB过F1,且垂直于x轴,并与双曲线交于A、B两点,若AO⊥BF2,则双曲线的离心率e = .
25.如图:已知线段AB = 4,动圆O1与线段AB相切于点C,且AC-BC =,过点A,B分别作⊙O1的两条切线,两切线相交于点P,且P、O1均在AB的同侧.
建立适当坐标系,当O1位置变化时,求动点P的轨迹E方程.
26.已知M(-1,0)、N(1,0),|PM|-|PN|=4,则动点P的轨迹________.
27.若实数m满足0<m<8,则曲线C1:与曲线C2:的( )
A.焦距相等 B.实半轴长相等
C.虚半轴长相等 D.离心率相等
28.与有相同的焦点,且过点(2,)的双曲线方程为 .
29.已知双曲线的渐近线方程是y=±x,则它的离心率是_____________.
30.己知中心在原点,焦点在坐标轴上的双曲线的离心率为,则其渐近线方程为 ,两渐近线的夹角的正切值为 .
31.已知中心在原点,坐标轴为对称轴,一条渐近线的方程为3x+2y = 0,且双曲线经过点R(8,6),求这个双曲线的方程.
32.若双曲线的渐近线的方程为y = ±3x,且经过点(2, 3),则双曲线的方程是 .
33.已知P(2,1),Q(3,-2),经过P,Q两点的双曲线的标准方程为 .
34.已知双曲线经过M(1,1),N(-2,5)两点,求双曲线的标准方程.
35.求以椭圆长轴上的顶点为焦点,椭圆焦点为顶点的双曲线方程.
36.已知双曲线的一个焦点与圆x2+y2-10x=0的圆心重合,且双曲线的离心率等于,则该双曲线的标准方程为________________.
1.B
2.D
3.4a
4.90°
5.
6.D
7.
8.
9.此双曲线的方程为,离心率为或者此双曲线的方程为,离心率为2.
10.
11.
12.
13.C.
详解:因为|MN| = 4,且|PM|-|PN| = 4,所以动点P的轨迹是一条射线.故选C.
14.D.
详解:两定圆O1、O2无公共点,它们的位置关系应是外离或内含:
设两定圆O1、O2的半径分别为r1,r2(r1>r2),圆O的半径为R,
当两圆外离时,|OO1| = R-r1,|OO2| = R-r2,∴|OO2|-|OO1| = r1-r2<|O1O2|,
∴圆心O的轨迹是双曲线的一支;
当两圆内含时,|OO1| = r1-R,|OO2| = R-r2,∴|OO2|+|OO1| = r1-r2>|O1O2|,
∴圆心O的轨迹是椭圆.
故选D.
15.A.
详解:由题意,圆(x+4)2+y2 = 1的圆心是(-4,0),圆(x-4)2+y2 = 1的圆心是(4,0),
双曲线的两个焦点坐标分别为(-4,0),(4,0),|PF1|-|PF2| = 2a = 6,
∴双曲线的焦点正好是两圆(x+4)2+y2 = 1和(x-4)2+y2 = 1的圆心,
∵两圆(x+4)2+y2 = 1和(x-4)2+y2 = 1的半径分别是r1 = 1,r2 = 1,
∴|PM|min = |PF1|-1,|PN|max = |PF2|+1,|PM|max = |PF1|+1,|PN|min = |PF2|-1,
∴(|PM|-|PN|)min =|PM|min-|PN|max=(|PF1|-1)-(|PF2|+1) = 6-2 = 4,
(|PM|-|PN|)max =|PM|max-|PN|min= (|PF1|+1)-(|PF2|-1) = 6+2 = 8,
∴|PM|-|PN|的取值范围是[4,8].故选A.
16.13.
详解:如图
圆C1:(x+4)2+y2 = 4的圆心为(-4,0),半径为r1 = 2,
圆C2:(x-4)2+y2 = 1的圆心为(4,0),半径为r2 = 1,
设双曲线的左右焦点坐标分别为F1(-4,0),F2(4,0),
连接PF1,PF2,F1M,F2N,可得
|PM|2-|PN|2 = (|PF1|2-r12)-(|PF2|2-r22)
= (|PF1|2-4)-(|PF2|2-1)
=|PF1|2-|PF2|2-3
= (|PF1|-|PF2|)(|PF1|+|PF2|)-3
= 2a(|PF1|+|PF2|)-3
= 2(|PF1|+|PF2|)-3≥2 2c-3 = 2 8-3 = 13.
当且仅当P为右顶点时,取得等号,即最小值13.
故答案为13.
17.4a+2m.
详解:如图,
∵|AF2|-|AF1| = 2a,|BF2|-|BF1| = 2a,
∴(|AF2|-|AF1|)+(|BF2|-|BF1|) = 4a,
又∵|AF1|+|BF1| = |AB| = m,
∴|AF2|+|BF2| = 4a+(|AF1|+|BF1|) = 4a+m.
∴△ABF2的周长等于|AF2|+|BF2|+|AB| = 4a+2m.
18..
详解:如图,
根据双曲线的标准方程(b>0),得a = 3,
由双曲线的定义可得|AF2|-|AF1| = 2a = 6 ①
|BF2|-|BF1| = 2a = 6 ②
①+②可得|AF2|+|BF2|-(|AF1|+|BF1|) = 12,
∵过双曲线的左焦点F1的直线交双曲线的左支于A,B两点,
∴|AF1|+|BF1| = |AB|,当|AB|是双曲线的通径时|AB|最小,通径长为.
∴|AF2|+|BF2|-(|AF1|+|BF1|)
= |AF2|+|BF2|-|AB| = 12.
∴|BF2|+|AF2| = |AB|+12≥+12 = 14,
∴b =.
19.4.
详解:在双曲线x2-y2 = 1中,a = b = 1,c =,
设P在右支上,则|PF1|-|PF2| = 2a = 2,
∵∠F1PF2 = 60°,
∴|F1F2|2 = |PF1|2+|PF2|2-2|PF1||PF2|cos60°
= (|PF1|-|PF2|)|2+2|PF1||PF2|-|PF1||PF2|,
即4c2 = 4a2+|PF1| |PF2|,
即|PF1| |PF2| = 4c2-4a2 = 4b2 = 4,
故答案为4.
20.16.
详解:根据双曲线的方程可知,a = 3,b = 4,c = 5,
则|F1F2| = 2c = 10,||PF1|-|PF2|| = 2a = 2×3 = 6,∴|PF1|2+|PF2|2-2|PF1||PF2| = 36,
∴|PF1|2+|PF2|2 = 100 = |F1F2|2,∴∠F1PF2 = 90°,
∴△F1PF2的面积为|PF1| |PF2| = 32×= 16.
也可用焦点三角形面积公式S△F1PF2=b2cot=16×1=16.
21.-1.
详解:双曲线mx2+y2 = 1即,
∴e2 ==1+ = 2,∴m =-1.
故答案为-1.
22.或.
详解:∵A =-2B ≠ 0,∴A,B符号相反,
①若A>0,则方程等价为,为双曲线,其中a2 =,b2 =,
则c2 ==-,则e2 == 3,即离心率e =,
②若A<0,则方程等价为,为双曲线,其中a2 =,b2 =-,
则c2 = =+,则e2 =,即离心率e = .
23.2.
详解:∵过双曲线的右焦点F作与实轴垂直的直线交双曲线E于B,C两点,∴设x = c,得,解之得y = ±,得B(c,)、C(c,-)
∵左顶点A(-a,0)与B、C构成直角三角形,
∴根据双曲线的对称性,得A到BC的距离等于BC长的一半,
可得c+a =,即c+a =,化简得c2-ac-2a2 = 0,
两边都除以a2,得e2-e-2 = 0,解之得e = 2(舍负),即双曲线E的离心率为2.
故答案为2.
24..
详解:由题意得:F1(-c,0),F2(c,0),A(-c,),B(-c,-),
∴直线AO的斜率k1 =,直线BF2的斜率k2 =,
∵AO⊥BF2,∴k1k2 =-1,即×= 1,∴b4 = 2a2c2,
又∵b2 = c2-a2,∴(c2-a2)2 = 2a2c2,解之得,又由于,
所以.
25..
详解:以AB为x轴,AB的垂直平分线为y轴,建立坐标系,令PA、PB与圆的切点分别为M、N.
∴|PM|=|PN|,|AM|=|AC|,|BC|=|BN|,
则|PA|-|PB| = |AC|-|BC| = ,
∴点P在以A、B为焦点双曲线的一支上,且2c = 4,2a =,
∴c = 2,a =,∴b =,
∴P点的轨迹E为.
26.不存在.
因为|MN|=2,且|PM|-|PN|=4>|MN|,所以动点P的轨迹不存在.
27.A.
详解:由于0<m<8,则0<8-m<8,16<24-m<24,
即曲线C1:表示焦点在x轴上的双曲线,
其中a2=24,b2=8-m,c2=32-m,
曲线C2:表示焦点在x轴上的双曲线,
其中a ’2=24-m,b’2=8,c’2=32-m,
即两个双曲线的焦距相等,故选:A.
28..
详解:设方程为,将点(2,)代入方程得λ = 1.
所以方程为.故答案为.
29.
详解:∵双曲线的渐近线方程是y=±x,
∴或,可得a=b,
∴离心率e=.
30.y = ±x或y = ±2x;.
详解:由题意可得e =,即为c =,由b2 = c2-a2 =a2,即a = 2b,
当焦点在x轴上时,渐近线方程为y = ±x,即为y = ±x;
当焦点在y轴上时,渐近线方程为y = ±x,即为y = ±2x;
当焦点在x轴上时,根据正切的二倍角公式,两渐近线的夹角的正切为;
同理,当焦点在y轴上时,由于夹角是锐角或直角,所以两渐近线的夹角的正切为.
31..
详解:因为双曲线的渐近线方程为3x+2y = 0,所以设曲线的标准方程为9x2-4y2 = λ,
因为双曲线过点R(8,6),所以9×64-4×108 = 144 = λ,
所以曲线的标准方程为9x2-4y2 = 144,即.
32..
详解:由题意可知,可设双曲线的方程是,
把点(2, 3)代入方程解得k = 1,
故所求的双曲线的方程是.
33..
详解:设所求双曲线方程为mx2+ny2 = 1(mn < 0),
∵P(2,1),Q(3,-2)两点在双曲线上,∴,
∴经过P,Q两点的双曲线的标准方程为.
34..
详解:设所求双曲线方程为mx2+ny2 = 1(mn < 0),
∵M(1,1),N(-2,5)两点在双曲线上,∴,
∴双曲线方程是,整理得.
35..
详解:椭圆的长轴顶点为(0,-2)和(0,2),
焦点为(0,-2)和(0,2),
∴双曲线的焦点坐标是(0,-2)和(0,2),顶点为(0,-2)和(0,2),
∴双曲线方程为.
36..
详解:圆x2+y2-10x=0化成标准方程得(x-5)2+y2=25,
∴圆的圆心坐标为(5,0),即双曲线的焦点坐标为F(5,0),
∵双曲线的离心率等于,
∴,
∴,
∴双曲线的标准方程为.
