2012高一物理课件:第二章 章末整合(粤教版必修2)
文档属性
| 名称 | 2012高一物理课件:第二章 章末整合(粤教版必修2) |  | |
| 格式 | zip | ||
| 文件大小 | 390.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-08-28 16:25:37 | ||
图片预览




文档简介
(共16张PPT)
专题一
水平面内的圆周运动问题
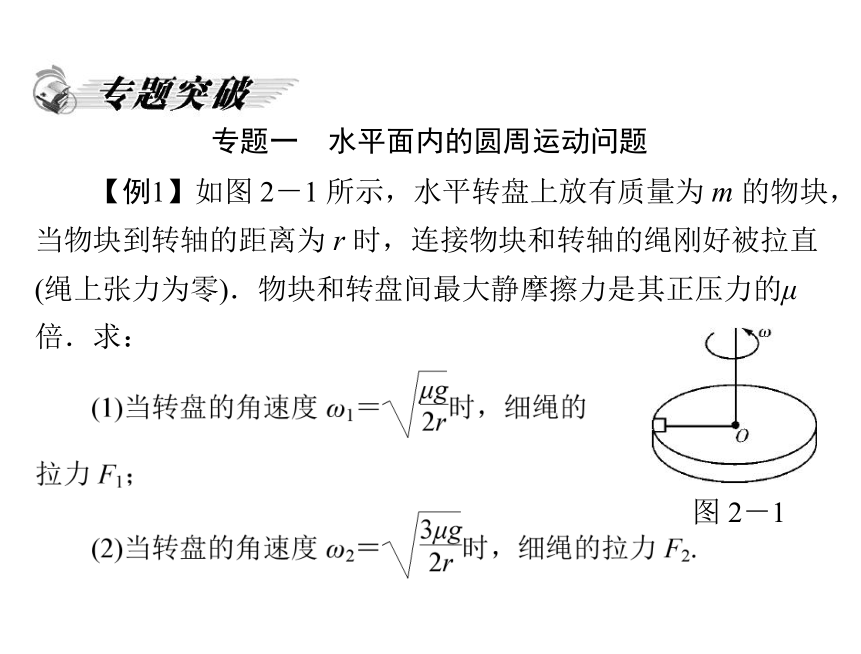
【例1】如图 2-1 所示,水平转盘上放有质量为 m 的物块,
当物块到转轴的距离为 r 时,连接物块和转轴的绳刚好被拉直
(绳上张力为零).物块和转盘间最大静摩擦力是其正压力的μ
倍.求:
图 2-1
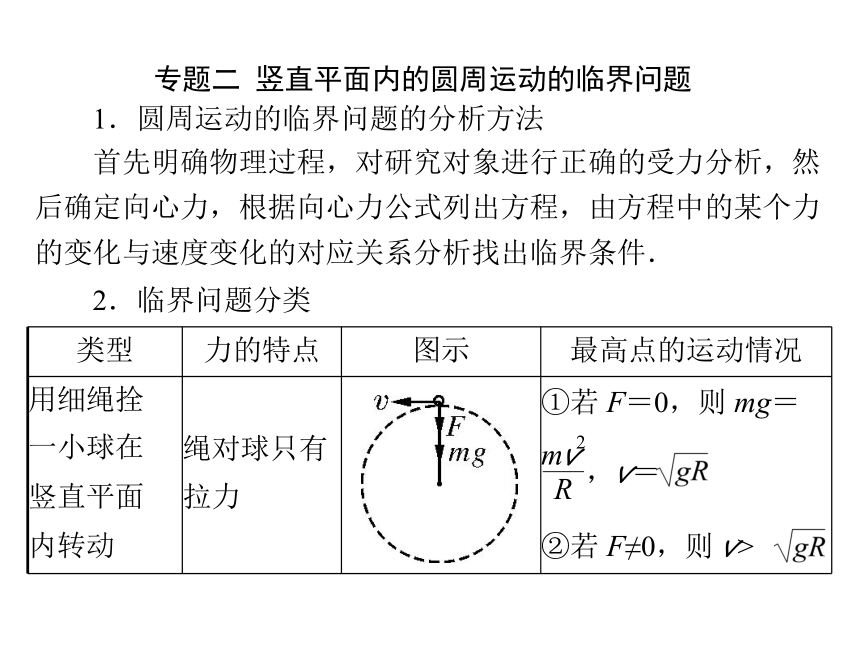
类型 力的特点 图示 最高点的运动情况
用细绳拴
一小球在
竖直平面
内转动 绳对球只有
拉力 ①若 F=0,则 mg=
2
mv
,v=
R
②若 F≠0,则 v>
专题二 竖直平面内的圆周运动的临界问题
1.圆周运动的临界问题的分析方法
首先明确物理过程,对研究对象进行正确的受力分析,然
后确定向心力,根据向心力公式列出方程,由方程中的某个力
的变化与速度变化的对应关系分析找出临界条件.
2.临界问题分类
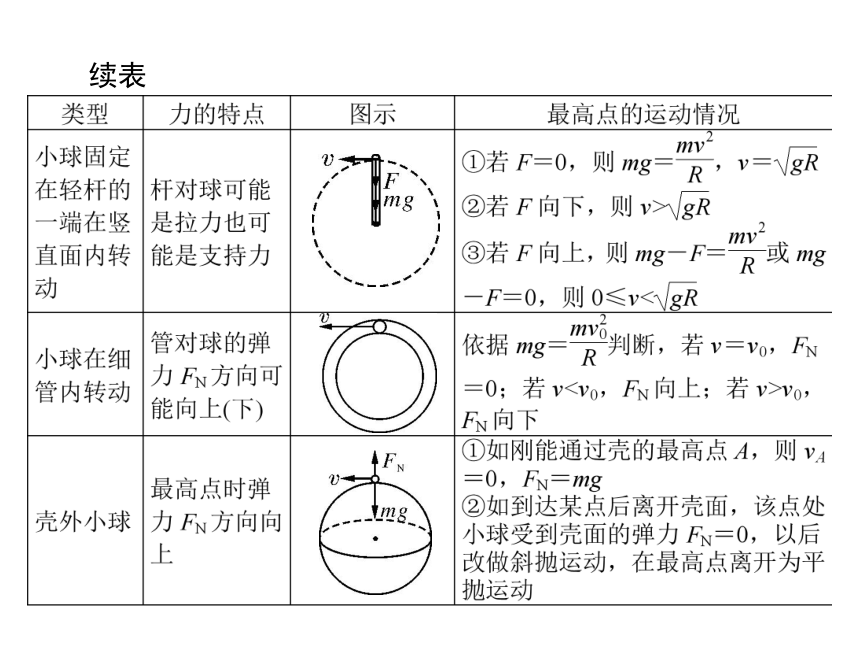
续表
【例2】长为 L 的细绳,一端系一质量为 m 的小球,另一
端固定于某点,当绳竖直时小球静止.现给小球一水平初速度
v0,使小球在竖直平面内做圆周运动,并且刚好能过最高点,
则下列说法中正确的是(
)
A.球过最高点时,速度为零
B.球过最高点时,绳的拉力为 mg
答案:D
【例 3】(双选)如图 2-2 所示,细杆的一端与一小球相连,
可绕过 O 点的水平轴自由转动.现给小球一初速度,使它做圆
周运动,图中 a、b 分别表示小球轨道的最低点和最高点,则杆
对小球的作用力可能是(
)
图 2-2
A.a 处为拉力,b 处为拉力
B.a 处为拉力,b 处为推力
C.a 处为推力,b 处为拉力
D.a 处为推力,b 处为推力
解析:小球在最高点 b 的速度大于
时,b 处为拉力;小球的速度在 0<v< 时,
b 处为推力;小球在最低点时,杆对小球的作用力一定是拉力.
答案:AB
【例4】如图 2-3 所示为一圆拱桥,最高点的半径为 40 m.
一辆质量为 1.2×103 kg 的小车,以 10 m/s 的速度经过拱桥的最
高点,此时车对桥顶部的压力大小是多少?若车在最高点时,
车对桥面的压力恰好为零,车的速度是多少?(取 g=10 m/s2)
图 2-3
解:设小车以v0=10 m/s 的速度经过拱桥的最高点时,桥
顶对小车的支持力为N,则根据牛顿第二定律有
把 v0=10 m/s、R=40 m 代入上式可解得N=9 000 N
根据牛顿第三定律,可知小车对桥顶部的压力大小为9 000 N.
当车在最高点对桥面的压力为零时,根据牛顿第二定律有
mg=m
v2
R
解得小车的速度v=20 m/s.
1.(2011 年安徽卷)一般的曲线运动可以分成很多小段,每
小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同
半径的小圆弧来代替.如图 2-4 (a)所示,曲线上的 A 点的曲率
圆定义为:通过 A 点和曲线上紧邻 A 点两侧的两点作一圆,在极
限情况下,这个圆就叫做 A 点的曲率圆,其半径ρ叫做 A 点的曲
率半径.现将一物体沿与水平面成α角的方向以速度 v0 抛出,如
图 2-4(b)所示.则在其轨迹最高点 P 处的曲率半径是(
)
图 2-4
答案:C
2.(双选,2011 年汕头质检)如图 2-5 所示,关于转动的
)
BD
门扇上的 A、B 两点,说法正确的是(
A.角速度ωA>ωB
B.角速度ωA=ωB
C.向心加速度aA>aB
D.线速度vA< vB
图 2-5
3.(双选,2011 年增城调研)洗衣机的甩干筒在旋转时有衣
服附在筒壁上,则此时(
)
BD
A.衣服受重力、筒壁的弹力和摩擦力,及离心力作用
B.衣服随筒壁做圆周运动的向心力由筒壁的弹力提供
C.筒壁对衣服的摩擦力随转速的增大而增大
D.筒壁对衣服的弹力随着衣服含水量的减少而减少
4.(2010 年上海卷)月球绕地球做匀速圆周运动的向心加速
度大小为 a,设月球表面的重力加速度大小为 g1,在月球绕地
球运行的轨道处由地球引力产生的加速度大小为 g2,则(
)
B
A.g1=a
C.g1+g2=a
B.g2=a
D.g2-g1=a
解析:根据月球绕地球做匀速圆周运动的向心力由地球引
力提供,选 B.
专题一
水平面内的圆周运动问题
【例1】如图 2-1 所示,水平转盘上放有质量为 m 的物块,
当物块到转轴的距离为 r 时,连接物块和转轴的绳刚好被拉直
(绳上张力为零).物块和转盘间最大静摩擦力是其正压力的μ
倍.求:
图 2-1
类型 力的特点 图示 最高点的运动情况
用细绳拴
一小球在
竖直平面
内转动 绳对球只有
拉力 ①若 F=0,则 mg=
2
mv
,v=
R
②若 F≠0,则 v>
专题二 竖直平面内的圆周运动的临界问题
1.圆周运动的临界问题的分析方法
首先明确物理过程,对研究对象进行正确的受力分析,然
后确定向心力,根据向心力公式列出方程,由方程中的某个力
的变化与速度变化的对应关系分析找出临界条件.
2.临界问题分类
续表
【例2】长为 L 的细绳,一端系一质量为 m 的小球,另一
端固定于某点,当绳竖直时小球静止.现给小球一水平初速度
v0,使小球在竖直平面内做圆周运动,并且刚好能过最高点,
则下列说法中正确的是(
)
A.球过最高点时,速度为零
B.球过最高点时,绳的拉力为 mg
答案:D
【例 3】(双选)如图 2-2 所示,细杆的一端与一小球相连,
可绕过 O 点的水平轴自由转动.现给小球一初速度,使它做圆
周运动,图中 a、b 分别表示小球轨道的最低点和最高点,则杆
对小球的作用力可能是(
)
图 2-2
A.a 处为拉力,b 处为拉力
B.a 处为拉力,b 处为推力
C.a 处为推力,b 处为拉力
D.a 处为推力,b 处为推力
解析:小球在最高点 b 的速度大于
时,b 处为拉力;小球的速度在 0<v< 时,
b 处为推力;小球在最低点时,杆对小球的作用力一定是拉力.
答案:AB
【例4】如图 2-3 所示为一圆拱桥,最高点的半径为 40 m.
一辆质量为 1.2×103 kg 的小车,以 10 m/s 的速度经过拱桥的最
高点,此时车对桥顶部的压力大小是多少?若车在最高点时,
车对桥面的压力恰好为零,车的速度是多少?(取 g=10 m/s2)
图 2-3
解:设小车以v0=10 m/s 的速度经过拱桥的最高点时,桥
顶对小车的支持力为N,则根据牛顿第二定律有
把 v0=10 m/s、R=40 m 代入上式可解得N=9 000 N
根据牛顿第三定律,可知小车对桥顶部的压力大小为9 000 N.
当车在最高点对桥面的压力为零时,根据牛顿第二定律有
mg=m
v2
R
解得小车的速度v=20 m/s.
1.(2011 年安徽卷)一般的曲线运动可以分成很多小段,每
小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同
半径的小圆弧来代替.如图 2-4 (a)所示,曲线上的 A 点的曲率
圆定义为:通过 A 点和曲线上紧邻 A 点两侧的两点作一圆,在极
限情况下,这个圆就叫做 A 点的曲率圆,其半径ρ叫做 A 点的曲
率半径.现将一物体沿与水平面成α角的方向以速度 v0 抛出,如
图 2-4(b)所示.则在其轨迹最高点 P 处的曲率半径是(
)
图 2-4
答案:C
2.(双选,2011 年汕头质检)如图 2-5 所示,关于转动的
)
BD
门扇上的 A、B 两点,说法正确的是(
A.角速度ωA>ωB
B.角速度ωA=ωB
C.向心加速度aA>aB
D.线速度vA< vB
图 2-5
3.(双选,2011 年增城调研)洗衣机的甩干筒在旋转时有衣
服附在筒壁上,则此时(
)
BD
A.衣服受重力、筒壁的弹力和摩擦力,及离心力作用
B.衣服随筒壁做圆周运动的向心力由筒壁的弹力提供
C.筒壁对衣服的摩擦力随转速的增大而增大
D.筒壁对衣服的弹力随着衣服含水量的减少而减少
4.(2010 年上海卷)月球绕地球做匀速圆周运动的向心加速
度大小为 a,设月球表面的重力加速度大小为 g1,在月球绕地
球运行的轨道处由地球引力产生的加速度大小为 g2,则(
)
B
A.g1=a
C.g1+g2=a
B.g2=a
D.g2-g1=a
解析:根据月球绕地球做匀速圆周运动的向心力由地球引
力提供,选 B.
同课章节目录
