2021-2022学年数学人教A版(2019)选择性必修第一册2.2.2 直线的两点式方程 课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)选择性必修第一册2.2.2 直线的两点式方程 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 624.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第二章 直线和圆的方程
2.2.2 直线的两点式方程
一、创设情境 引入新课
如图,植树时,只要定出两个树坑的位置就能够确定同一行的树坑所在的直线。生活中“两点确定一条直线”的例子随处可见,那么在直角坐标系内,两点是如何确定一条直线的呢?
二、探究本质得新知
探究一:直线的两点式方程及截距式方程
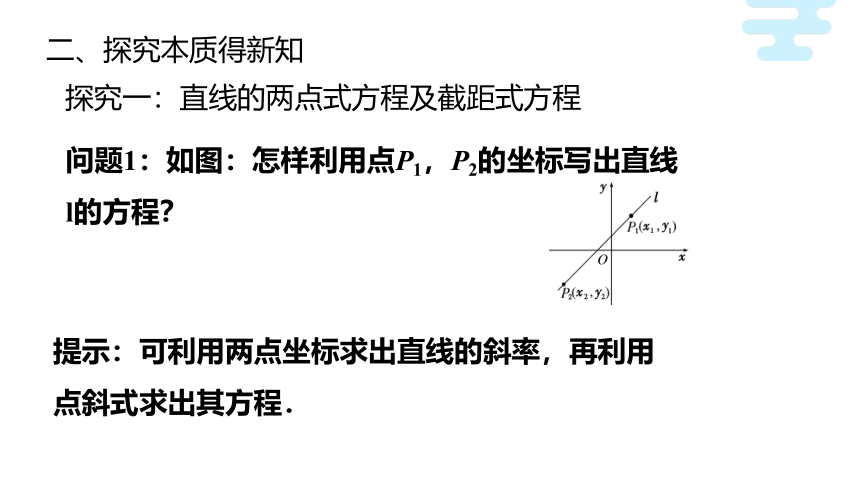
提示:可利用两点坐标求出直线的斜率,再利用点斜式求出其方程.
问题1:如图:怎样利用点P1,P2的坐标写出直线l的方程?
二、探究本质得新知
问题2:当x1≠x2,y1≠y2时,过P1,P2两点的直线的方程是什么?
探究一:直线的两点式方程及截距式方程
提示:过P1,P2两点的直线的斜率为 ,所以由点斜式得方程 ,即: (x1≠x2,y1≠y2)
二、探究本质得新知
探究一:直线的两点式方程及截距式方程
提示:结合条件可知直线过点(a,0),(0,b),利用两点式可求出直线的方程.
问题3:观察下面坐标系中的直线,由图中的条件能否求出直线的方程?
二、探究本质得新知
探究一:直线的两点式方程及截距式方程
直线的两点式方程和截距式方程
二、探究本质得新知
问题4:给定两点A(x1,y1),B(x2,y2)是否就可以用两点式写出直线AB的方程?
提示:不一定.只有在x1≠x2,y1≠y2的前提下才能写出直线的两点式.
当x1=x2时,直线方程为x=x1;
当y1=y2时,直线方程为y=y1.
探究一:直线的两点式方程及截距式方程
二、探究本质得新知
问题5:直线的截距式方程不能表示什么样的直线?
提示:截距式不能表示过原点的直线、与x轴垂直的直线、与y轴垂直的直线.
探究一:直线的两点式方程及截距式方程
三、举例应用,掌握定义
例1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中
(1)求BC边的方程;
(2)求BC边上的中线所在直线的方程.
三、举例应用,掌握定义
【解析】(1)因为BC边过两点B(5,-4),C(0,-2),所以由两点式得 ,即2x+5y+10=0.故BC边的方程为2x+5y+10=0(0≤x≤5).
(2)设BC的中点为M(x0,y0),
则x0= , .所以M ,又BC边上的中线经过点A(-3,2).所以由两点式得 ,即10x+11y+8=0.故BC边上的中线所在直线的方程为10x+11y+8=0.
三、举例应用,掌握定义
例2. 求经过点P(–2,3),且满足下列条件的直线方程:
(1)在x轴、y轴上的截距之和等于6;
(2)在x轴、y轴上的截距分别为a,b,且满足b=2a.
【解析】(1)设直线方程为 ,因为直线过点P(–2,3),所以 ,整理得a2–a–12=0,解得a=–3或4.于是所求直线方程为 或
三、举例应用,掌握定义
(2)①当a≠0时,设直线方程为 ,
将P(–2,3)代入,得 ,解得 ,
此时直线方程为 ;
②当a=0时,直线过点(0,0)和(–2,3),
所以直线的斜率为 ,此时直线的方程为 .
综上可知,所求直线方程为 或 .
三、举例应用,掌握定义
例3:三角形ABC的一个顶点是 , 的平分线方程分别为 。
(1)求直线BC 的方程.
(2)求直线AB的方程.
三、举例应用,掌握定义
【解析】(1)因为 的平分线方程分别为 ,所以直线AB与BC关于 对称,直线AC与BC关于 对称。点A(-3,1)关于 的对称点 在直线BC上,A关于 的对称点 也在直线BC上,由两点式得直线BC的方程为 ,即 .
(2)因为直线AB与直线BC关于 对称,所以直线AB与BC的斜率互为相反数,由(1)知,直线BC的斜率为2,所以直线AB的斜率为-2,又因为点A(-3,1)在直线AB上,所以直线AB的方程为: 即
四、学生练习,加深理解
1.过P1(2,0)、P2(0,3)两点的直线方程是( )
A. B.
C. D.
【解析】选C. 由截距式得,所求直线的方程为
四、学生练习,加深理解
2. 过点 (-1,-3)和(2,4) 的直线方程是( )
A. B.
C. D.
【解析】选B. 由直线方程的两点式得: ,整理得:
四、学生练习,加深理解
3. 直线 在x轴,y轴上的截距分别为( )
A.2,3 B.-2,3 C.-2,-3 D.2,-3
【解析】选D. 因为 ,
当 x=0时, y=-3,即在 y轴上的截距为-3 ;
当y=0 时,x=2,即在x轴上的截距为 2
四、学生练习,加深理解
4.经过 两点 的直线方程______.
【解析】直线方程为 ,即 .
答案:
四、学生练习,加深理解
5.三角形的顶点坐标为A(0,-5),B(-3,3),C(2,0),求直线AB和直线AC的方程.
四、学生练习,加深理解
【解析】因为直线AB过点A(0,-5),B(-3,3)两点,
由两点式方程,得 .整理得8x+3y+15=0.
所以直线AB的方程为8x+3y+15=0.
又∵直线AC过A(0,-5),C(2,0)两点,
由截距式得 ,整理得5x-2y-10=0,
所以直线AC的方程为5x-2y-10=0.
师:这节课你有什么收获?
生:1.知识方面:(1)掌握了直线的两点式方程及适用范围。
(2)掌握了直线的截距式方程及适用范围
2.能力方面:能够用所学知识求满足条件的直线的方程。
3.思想方面:体升了数学运算素养和数形结合的能力
五、归纳小结 提高认识
六、作业布置 检测目标
教材P67 4,7,13题
第二章 直线和圆的方程
2.2.2 直线的两点式方程
一、创设情境 引入新课
如图,植树时,只要定出两个树坑的位置就能够确定同一行的树坑所在的直线。生活中“两点确定一条直线”的例子随处可见,那么在直角坐标系内,两点是如何确定一条直线的呢?
二、探究本质得新知
探究一:直线的两点式方程及截距式方程
提示:可利用两点坐标求出直线的斜率,再利用点斜式求出其方程.
问题1:如图:怎样利用点P1,P2的坐标写出直线l的方程?
二、探究本质得新知
问题2:当x1≠x2,y1≠y2时,过P1,P2两点的直线的方程是什么?
探究一:直线的两点式方程及截距式方程
提示:过P1,P2两点的直线的斜率为 ,所以由点斜式得方程 ,即: (x1≠x2,y1≠y2)
二、探究本质得新知
探究一:直线的两点式方程及截距式方程
提示:结合条件可知直线过点(a,0),(0,b),利用两点式可求出直线的方程.
问题3:观察下面坐标系中的直线,由图中的条件能否求出直线的方程?
二、探究本质得新知
探究一:直线的两点式方程及截距式方程
直线的两点式方程和截距式方程
二、探究本质得新知
问题4:给定两点A(x1,y1),B(x2,y2)是否就可以用两点式写出直线AB的方程?
提示:不一定.只有在x1≠x2,y1≠y2的前提下才能写出直线的两点式.
当x1=x2时,直线方程为x=x1;
当y1=y2时,直线方程为y=y1.
探究一:直线的两点式方程及截距式方程
二、探究本质得新知
问题5:直线的截距式方程不能表示什么样的直线?
提示:截距式不能表示过原点的直线、与x轴垂直的直线、与y轴垂直的直线.
探究一:直线的两点式方程及截距式方程
三、举例应用,掌握定义
例1.已知A(-3,2),B(5,-4),C(0,-2),在△ABC中
(1)求BC边的方程;
(2)求BC边上的中线所在直线的方程.
三、举例应用,掌握定义
【解析】(1)因为BC边过两点B(5,-4),C(0,-2),所以由两点式得 ,即2x+5y+10=0.故BC边的方程为2x+5y+10=0(0≤x≤5).
(2)设BC的中点为M(x0,y0),
则x0= , .所以M ,又BC边上的中线经过点A(-3,2).所以由两点式得 ,即10x+11y+8=0.故BC边上的中线所在直线的方程为10x+11y+8=0.
三、举例应用,掌握定义
例2. 求经过点P(–2,3),且满足下列条件的直线方程:
(1)在x轴、y轴上的截距之和等于6;
(2)在x轴、y轴上的截距分别为a,b,且满足b=2a.
【解析】(1)设直线方程为 ,因为直线过点P(–2,3),所以 ,整理得a2–a–12=0,解得a=–3或4.于是所求直线方程为 或
三、举例应用,掌握定义
(2)①当a≠0时,设直线方程为 ,
将P(–2,3)代入,得 ,解得 ,
此时直线方程为 ;
②当a=0时,直线过点(0,0)和(–2,3),
所以直线的斜率为 ,此时直线的方程为 .
综上可知,所求直线方程为 或 .
三、举例应用,掌握定义
例3:三角形ABC的一个顶点是 , 的平分线方程分别为 。
(1)求直线BC 的方程.
(2)求直线AB的方程.
三、举例应用,掌握定义
【解析】(1)因为 的平分线方程分别为 ,所以直线AB与BC关于 对称,直线AC与BC关于 对称。点A(-3,1)关于 的对称点 在直线BC上,A关于 的对称点 也在直线BC上,由两点式得直线BC的方程为 ,即 .
(2)因为直线AB与直线BC关于 对称,所以直线AB与BC的斜率互为相反数,由(1)知,直线BC的斜率为2,所以直线AB的斜率为-2,又因为点A(-3,1)在直线AB上,所以直线AB的方程为: 即
四、学生练习,加深理解
1.过P1(2,0)、P2(0,3)两点的直线方程是( )
A. B.
C. D.
【解析】选C. 由截距式得,所求直线的方程为
四、学生练习,加深理解
2. 过点 (-1,-3)和(2,4) 的直线方程是( )
A. B.
C. D.
【解析】选B. 由直线方程的两点式得: ,整理得:
四、学生练习,加深理解
3. 直线 在x轴,y轴上的截距分别为( )
A.2,3 B.-2,3 C.-2,-3 D.2,-3
【解析】选D. 因为 ,
当 x=0时, y=-3,即在 y轴上的截距为-3 ;
当y=0 时,x=2,即在x轴上的截距为 2
四、学生练习,加深理解
4.经过 两点 的直线方程______.
【解析】直线方程为 ,即 .
答案:
四、学生练习,加深理解
5.三角形的顶点坐标为A(0,-5),B(-3,3),C(2,0),求直线AB和直线AC的方程.
四、学生练习,加深理解
【解析】因为直线AB过点A(0,-5),B(-3,3)两点,
由两点式方程,得 .整理得8x+3y+15=0.
所以直线AB的方程为8x+3y+15=0.
又∵直线AC过A(0,-5),C(2,0)两点,
由截距式得 ,整理得5x-2y-10=0,
所以直线AC的方程为5x-2y-10=0.
师:这节课你有什么收获?
生:1.知识方面:(1)掌握了直线的两点式方程及适用范围。
(2)掌握了直线的截距式方程及适用范围
2.能力方面:能够用所学知识求满足条件的直线的方程。
3.思想方面:体升了数学运算素养和数形结合的能力
五、归纳小结 提高认识
六、作业布置 检测目标
教材P67 4,7,13题
