3.3幂函数(知识梳理+例题+变式+练习)(解析版)
文档属性
| 名称 | 3.3幂函数(知识梳理+例题+变式+练习)(解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-27 07:22:23 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
3.3幂函数
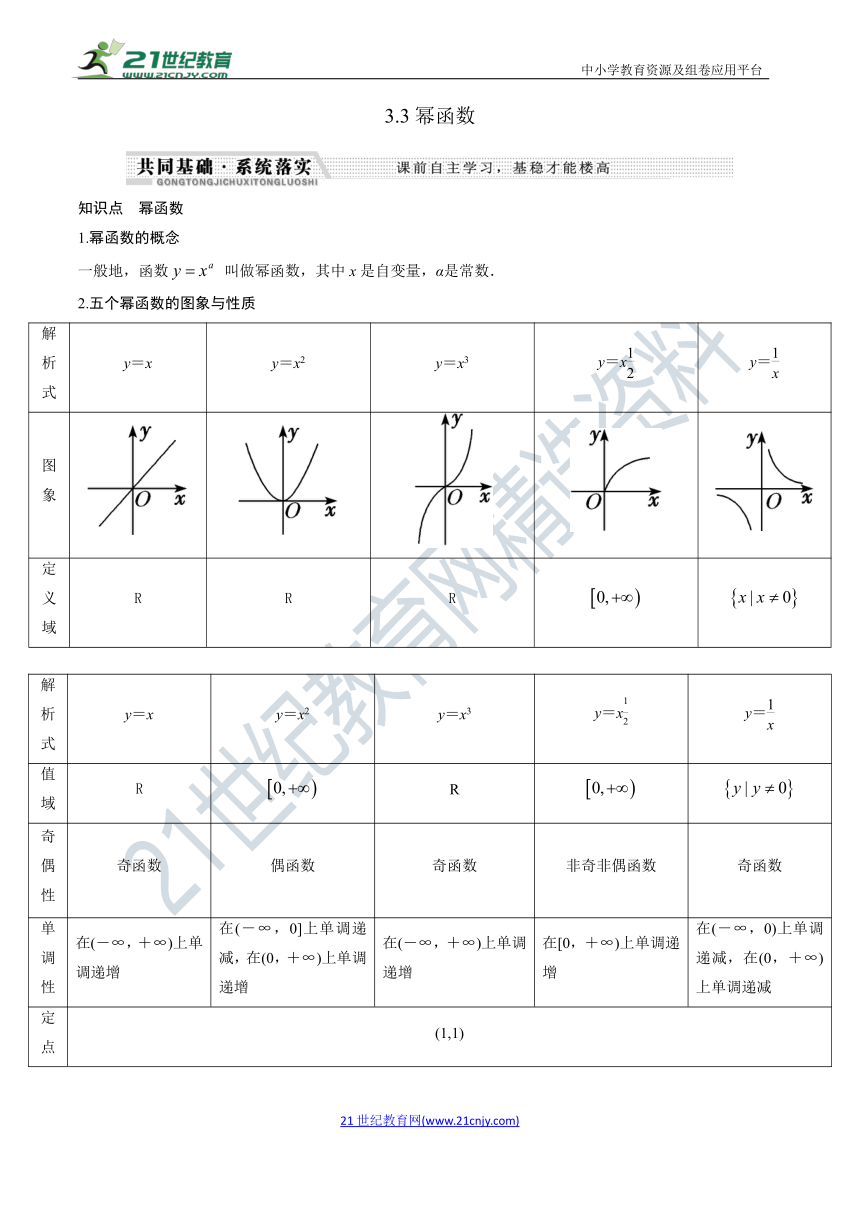
知识点 幂函数
1.幂函数的概念
一般地,函数 叫做幂函数,其中x是自变量,α是常数.
2.五个幂函数的图象与性质
解析式 y=x y=x2 y=x3 y=x y=
图象
定义域 R R R
解析式 y=x y=x2 y=x3 y=x y=
值域 R R
奇偶性 奇函数 偶函数 奇函数 非奇非偶函数 奇函数
单调性 在(-∞,+∞)上单调递增 在(-∞,0]上单调递减,在(0,+∞)上单调递增 在(-∞,+∞)上单调递增 在[0,+∞)上单调递增 在(-∞,0)上单调递减,在(0,+∞)上单调递减
定点 (1,1)
【思考】
通过5个幂函数图象的观察,哪个象限一定有幂函数的图象?哪个象限一定没有幂函数的图象?
【提示】
第一象限一定有幂函数的图象,第四象限一定没有幂函数的图象
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)幂函数的图象必过点(0,0)和(1,1). ( )
(2)幂函数的图象都不过第二、四象限. ( )
(3)当幂指数α取1,3,时,幂函数y=xα是增函数. ( )
(4)若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大. ( )
【答案】(1)×(2)×(3)√(4)×
2.已知幂函数的图象过点(2,4),则其解析式为( )
A.y=x+2 B.y=x2 C.y= D.y=x3
【答案】B
【解析】设幂函数的解析式为y=xα,当x=2时,y=4,故2α=4,即α=2.
3.在下列四个图形中, 的大致图象是 ( )
【答案】D
【解析】函数的定义域为(0,+∞),是减函数.故选D.
4.已知f(x)=(m-1)x是幂函数,则m=________.
【解析】2
【解析】∵函数f(x)=(m-1)x是幂函数,∴m-1=1,即m=2.
5.已知幂函数f(x)=xα图象过点,则f(4)=________.
【答案】
【解析】∵幂函数f(x)=xα的图象过点,∴2α=,∴α=-.即f(x)=x,∴f(4)=4=.
题型一 幂函数的概念
【探究发现】
幂函数的解析式有什么特征
【提示】(1)指数为常数
(2)底数是自变量,自变量的系数为1,
(3)幂的系数为1
(4)只有1项
【学透用活】
【例1】 (1)下列函数:
①y=x3;②y=x;
③y=4x2;④y=x5+1;
⑤y=(x-1)2;⑥y=x;⑦y=ax(a>1).
其中幂函数的个数为 ( )
A.1 B.2 C.3 D.4
【答案】B
【解析】由幂函数的概念可知,只有是幂函数
(2) 若f(x)=(m2-4m-4)xm是幂函数,则m=________.
【答案】5或-1
【解析】(2)因为f(x)=(m2-4m-4)xm是幂函数,所以m2-4m-4=1,即m2-4m-5=0,解得m=5或m=-1.
【方法技巧】
求幂函数解析式的依据和常用方法
(1)依据:若一个函数为幂函数,则该函数应具备幂函数解析式所具备的特征,这是解决与幂函数有关问题的隐含条件.
(2)常用方法:设幂函数解析式为f(x)=xα,依据条件求出α.
【变式训练】
1.在函数y=,y=2x3,y=x2+x,y=1中,幂函数的个数为 ( )
A.0 B.1 C.2 D.3
【解析】因为y==x-2,所以是幂函数;y=2x3由于出现系数2,因此不是幂函数;y=x2+x是两项和的形式,不是幂函数;y=1=x0(x≠0),可以看出,常数函数y=1 的图象比幂函数y=x0的图象多了一个点(0,1),所以常数函数y=1不是幂函数.
2.已知幂函数f(x)=(m2-4m+4)x在(0,+∞)为增函数,则m的值为 ( ) A.1或3 B.3 C.2 D.1
【答案】D
【解析】由函数f(x)为幂函数,得m2-4m+4=1,解得m=1或m=3.
又幂函数f(x)单调递增,则m2-6m+8>0,据此可得,m=1.
题型二 幂函数的图象及应用
【学透用活】
(1)幂函数y=xα在第一象限内的图象特征:
①当α>1时,图象过点(1,1),下凸递增,如y=x3;
②当0<α<1时,图象过点(1,1),上凸递增,如y=x;
③当α<0时,图象过点(1,1),下凸递减,且向两坐标轴无限地逼近,如y=x-1.
(2)幂函数在第一象限内指数的变化规律:
在第一象限内直线x=1的右侧,图象从上到下,相应的指数由大变小;在直线x=1的左侧,图象从下到上,相应的指数由大变小.
(3)幂函数的图象一定会出现在第一象限内,一定不会出现在第四象限内,至于是否出现在第二、三象限内,要看函数的奇偶性;幂函数的图象最多只能同时出现在两个象限内;如果幂函数的图象与坐标轴相交,则交点一定是原点.
【例2】若点(,2)在幂函数f(x)的图象上,点在幂函数g(x)的图象上,问当x为何值时,(1)f(x)>g(x);(2)f(x)=g(x);(3)f(x)<g(x).
【解析】设f(x)=xα,因为点(,2)在幂函数f(x)的图象上,所以将点(,2)代入f(x)=xα中,得2=()α,解得α=2,则f(x)=x2.同理可求得g(x)=x-2.
在同一坐标系中作出函数f(x)=x2和g(x)=x-2的图象(如图所示),观察图象可得:
(1)当x>1或x<-1时,f(x)>g(x);
(2)当x=1或x=-1时,f(x)=g(x);
(3)当-1<x<1且x≠0时,f(x)<g(x).
【方法技巧】
解决幂函数图象问题的原则
(1)依据图象高低判断幂指数大小,相关结论为:在(0,1)上,指数越大,幂函数图象越靠近x轴(简记为指大图低);在(1,+∞)上,指数越大,幂函数图象越远离x轴(简记为指大图高).
(2)当α>0时,幂函数的图象都经过(0,0)和(1,1)点,在第一象限内,当0<α<1时,曲线上凸;当α>1时,曲线下凸;当α<0时,幂函数的图象都经过(1,1)点,在第一象限内,曲线下凸.
【变式训练】
1.函数y=x-1的图象关于x轴对称的图象大致是 ( )
【答案】B
【解析】y=x的图象位于第一象限且为增函数,所以函数图象是上升的,函数y=x-1的图象可看作由y=x的图象向下平移一个单位得到的(如选项A中的图所示),将y=x-1的图象关于x轴对称后即为选项B.
2.若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图所示,则a,b,c,d的大小关系是 ( )
A.d>c>b>a B.a>b>c>d
C.d>c>a>b D.a>b>d>c
【答案】B
【解析】令a=2,b=,c=-,d=-1,正好和题目所给的形式相符合.在
第一象限内,x=1的右侧部分的图象,图象由下至上,幂指数增大,所
以a>b>c>d.故选B.
题型三 利用幂函数的单调性比较大小
【探究发现】
幂函数的单调性如何判断?
【提示】(1)幂函数y=xa 的单调性主要通过a的正负判断,并且在第一象限内单调性的规律体现的比较明显.
(2)a>0时,幂函数y=xa在第一象限内单调递增;a<0 时,幂函数y=xa在第一象限内单调递减.
【学透用活】
【例3】比较下列各组数中两个数的大小.
(1)0.5与0.5;
(2)-1与-1;
(3) 与.
【解析】(1)∵幂函数y=x0.5在(0,+∞)上是单调递增的,又>,∴0.5>0.5.
(2)∵幂函数y=x-1在(-∞,0)上是单调递减的,
又-<-,∴-1>-1.
(3)∵函数y1=x为(0,+∞)上的增函数,又>1,∴>1=1.
又∵函数y2=x在(0,+∞)上是增函数,且<1,∴<1=1,∴>.
【方法技巧】
1.比较幂的大小的三种基本方法
直接法 当幂指数相同时,可直接利用幂函数的单调性来比较
转化法 当幂指数不同时,可以先转化为相同幂指数,再运用单调性比较大小
中间量法 当底数不同且幂指数也不同时,不能运用单调性比较大小,可选取适当的中间值,从而达到比较大小的目的
2.利用幂函数单调性比较大小时的注意点
比较大小的实数必须在同一函数的同一单调区间内,否则无法比较大小.
【变式训练】
1. (多选)下列不等式在a<b<0的条件下能成立的是( )
A.a-1>b-1 B.a<b C.b2<a2 D.a>b
【答案】ABC
【解析】分别构造函数y=x-1,y=x,y=x2,y=x,其中函数y=x-1,y=x2在(-∞,0)上为减函数,
故A、C成立.而y=x,y=x为(-∞,0)上的增函数,从而B成立,D不成立.
2.比较下列各题中两个幂的值的大小:
(1)1.1,0.9;
(2)3,.
【解析】(1)因为y=x为(0,+∞)上的减函数,又1.1>0.9,所以1.1<0.9.
(2)因为3=,函数y=x为[0,+∞)上的增函数,且<,所以<,即3<.
题型四 幂函数性质的综合应用
【学透用活】
已知函数f(x)=x(m∈N*).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若该函数图象经过点(2,),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
【解析】(1)∵m2+m=m(m+1),m∈N*,
∴m与m+1中必定有一个为偶数,
∴该函数的定义域为[0,+∞),
由幂函数的性质知,该函数在定义域上单调递增.
(2)∵该函数图象过点(2,),∴2=,
∴m2+m=2,∴m=1(m∈N*).
由f(2-a)>f(a-1),得解得1≤a<.
故m的值为1,满足条件f(2-a)>f(a-1)的实数a的取值范围为.
【方法技巧】
解决幂函数的综合问题,应注意以下两点:
(1)充分利用幂函数的图象、性质解题,如图象所过定点、单调性、奇偶性等;
(2)注意运用常见的思想方法解题,如分类讨论思想、数形结合思想.
【变式训练】
已知幂函数f(x)=(m2-5m+7)x-m-1(m∈R)为偶函数.
(1)求f的值;
(2)若f(2a+1)=f(a),求实数a的值.
【解析】(1)函数f(x)=(m2-5m+7)x-m-1(m∈R)为幂函数,
∴m2-5m+7=1,解得m=2或m=3.
当m=2时,f(x)=x-3,不是偶函数,舍去;
当m=3时,f(x)=x-4,为偶函数,满足题意.
∴f(x)=x-4,∴f=-4==16.
(2)由f(2a+1)=f(a),可得(2a+1)-4=a-4,
即解得a=-1或a=-.
【课堂思维激活】
一、综合性——强调融会贯通
1.已知函数f(x)=(m2+m-1)xm是幂函数,且在(0,+∞)上是减函数.
(1)求实数m的值;
(2)请画出f(x)的大致图象;
(3)若f(2a-1)>f(a),a∈R成立,求a的取值范围.
【解析】(1)由函数f(x)是幂函数,
则m2+m-1=1,解得m=-2或m=1,
又因为f(x)在(0,+∞)上是减函数,
所以m=-2.
(2)由(1)知,f(x)=x-2,
则f(x)的大致图象如图所示:
(3)由(2)知,f(x)的图象关于y轴对称,且在(0,+∞)上递减,
则由f(2a-1)>f(a),得|2a-1|<|a|,
即(2a-1)2<a2,可得(a-1)(3a-1)<0,解得<a<1,又a≠,
∴a的取值范围为∪.
二、应用性——强调学以致用
2.为了保证信息的安全传输须使用加密方式,有一种方式其加密、解密原理为:发送方由明文到密文(加密),
接收方由密文到明文(解密).现在加密密钥为y=xα(α为常数),如“4”通过加密后得到密文“2”.若接收方接
到密文“3”,则解密后得到的明文是什么?
【解析】由题目可知加密密钥y=xα(α是常数)是一个幂函数模型,所以
要想求得解密后得到的明文,就必须先求出α的值.由题意得2=4α,解
得α=,则y=x.由x=3,得x=9.即解密后得到的明文是9.
三、创新性——强调创新意识和创新思维
3.已知幂函数y=xα的图象经过点A(0,0),B(1,1),C(-1,1),D(4,2)中的三点,写出满足条件的一个α值.
【解析】当α=2时,y=x2经过A,B,C三点.
当α=时,y=x经过A,B,D三点,答案不唯一.
1.如图给出四个幂函数的图象,则图象与函数大致对应的是( )
A.①y=x;②y=x2;③y=x3;④y=x-1
B.①y=x3;②y=x;③y=x2;④y=x-1
C.①y=x2;②y=x3;③y=x;④y=x-1
D.①y=x3;②y=x2;③y=x;④y=x-1
【答案】D
【解析】y=x3是奇函数,且在R上递增,对应题图①;y=x2是偶函数,对应题图②;y=x的定义域为[0,+∞),对应题图③;y=x-1的定义域为(-∞,0)∪(0,+∞),对应题图④.故选D.
2.已知幂函数f(x)=(2n2-n)xn+1,若f(x)在其定义域上为增函数,则n等于( )
A.1或- B.1
C.- D.-1或
【答案】C
【解析】依题意得2n2-n=1,即2n2-n-1=0,解得n=1或n=-.
当n=1时,f(x)=x2,在R上不是增函数,不符合题意,舍去;
当n=-时,f(x)=x=,在定义域[0,+∞)上是增函数,符合题意.故选C.
3.如图所示,曲线C1与C2分别是函数y=xm和y=xn在第一象限内的图象,则下列结论正确的是( )
A.nC.n>m>0 D.m>n>0
【答案】A
【解析】由图象可知,两函数在第一象限内递减,故m<0,n<0.当x=2时,2m>2n,所以n<m<0.
4.有四个幂函数:①f(x)=x-1;②f(x)=x-2;③f(x)=x3;④f(x)=x.某同学研究了其中的一个函数,他给出这个函数的三个性质:(1)偶函数;(2)值域是{y|y∈R,且y≠0};(3)在(-∞,0)上是增函数.如果他给出的三个性质中,有两个正确,一个错误,则他研究的函数是( )
A.① B.②
C.③ D.④
【答案】B
【解析】①f(x)=x-1只满足值域是{y|y∈R,且y≠0};③f(x)=x3只满足在(-∞,0)上是增函数;④f(x)=x只满足在(-∞,0)上是增函数,②f(x)=x-2是偶函数,在(-∞,0)上是增函数,但其值域是{y|y>0}.故选B.
5.已知幂函数f(x)=xa的图象过点,则函数g(x)=(x-2)f(x)在区间上的最小值是( )
A.-1 B.-2
C.-3 D.-4
【答案】C
【解析】由已知得2a=,解得a=-1,∴g(x)==1-在区间上单调递增,则g(x)min=g=-3.故选C.
6.已知幂函数f(x)=xα的部分对应值如表:
x 1
f(x) 1
则f(x)的单调递增区间是________.
【答案】 [0,+∞)
【解析】因为f =,所以α=,即α=,所以f(x)=x的单调递增区间是[0,+∞).
7.设α∈,则使f(x)=xα为奇函数且在(0,+∞)上单调递减的α的值是________.
【答案】-1
【解析】因为f(x)=xα为奇函数,所以α=-1,1,3.又因为f(x)在(0,+∞)上为减函数,所以α=-1.
8.若f(x)是幂函数,且满足=4,则f=________.
【答案】
【解析】设f(x)=xα,则f(4)=4α=22α,f(2)=2α.
∵==2α=4=22,
∴α=2,∴f(x)=x2,∴f =2=.
9.已知函数f(x)=(m2+2m)·xm2+m-1,m为何值时,函数f(x)是:(1)正比例函数;(2)反比例函数;(3)幂函数.
【解析】(1)若函数f(x)为正比例函数,则
∴m=1.
(2)若函数f(x)为反比例函数,则
∴m=-1.
(3)若函数f(x)为幂函数,则m2+2m=1,
∴m=-1±.
10.比较下列各组数的大小:
(1)3-和3.2-;
(2)和;
(3)4.1和3.8.
【解析】(1)函数y=x-在(0,+∞)上为减函数,又3<3.2,所以3->3.2-.
(2)=,=,函数y=x在(0,+∞)上为增函数,而>,所以>.
(3)4.1>1=1,0<3.8<1=1,
所以4.1>3.8.
11.幂函数y=xα(α≠0),当α取不同的正数时,在区间[0,1]上它们的图象是一簇曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xm,y=xn的图象三等分,即有BM=MN=NA,则mn等于( )
A.1 B.2
C.3 D.无法确定
【答案】A
【解析】由条件知,M,N,∴=m,=n,∴mn=n=n=,∴mn=1.故选A.
12.(多选)已知实数a,b满足等式a=b,则下列关系式中可能成立的是( )
A.0C.1【答案】AC
【解析】画出y=x与y=x的图象(如图),设a=b=m,作直线y=m.
从图象知,若m=0或1,则a=b;若01,则113.给出下面四个条件:①f(m+n)=f(m)+f(n);②f(m+n)=f(m)·f(n);③f(mn)=f(m)·f(n);④f(mn)=f(m)+f(n).如果m,n是幂函数y=f(x)定义域内的任意两个值,那么幂函数y=f(x)一定满足的条件的序号为________.
【答案】③
【解析】设f(x)=xα,则f(m+n)=(m+n)α,f(m)+f(n)=mα+nα,f(m)·f(n)=mα·nα=(mn)α,f(mn)=(mn)α,所以f(mn)=f(m)·f(n)一定成立,其他三个不一定成立,故填③.
14.已知幂函数f(x)= (m∈N*).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若函数f(x)的图象经过点(2,),试确定m的值,并求满足f(2-a)>f(a-1)的实数a的取值范围.
【解析】(1)∵m∈N*,
∴m2+m=m×(m+1)为偶数.
令m2+m=2k,k∈N*,则f(x)=,
∴f(x)的定义域为[0,+∞),且f(x)在[0,+∞)上为增函数.
(2)由题意可得=2=2,∴m2+m=2,解得m=1或m=-2(舍去),
∴f(x)=x.
由(1)知f(x)在定义域[0,+∞)上为增函数,
∴f(2-a)>f(a-1)等价于2-a>a-1≥0,解得1≤a<,故实数a的取值范围为.
15.已知幂函数f(x)=x (m-2)(m∈N)是偶函数,且在(0,+∞)上是减函数,求函数f(x)的解析式,并讨论g(x)=a-的奇偶性.
【解析】由f(x)=x (m-2)(m∈N)在(0,+∞)上是减函数,得(m-2)<0,∴m<2.
∵m∈N,∴m=0,1.∵f(x)是偶函数,∴只有当m=0时符合题意,故f(x)=x.
于是g(x)=-,g(-x)=+,且g(x)的定义域为(-∞,0)∪(0,+∞),关于原点对称.
当a≠0且b≠0时,g(x)既不是奇函数也不是偶函数;
当a=0且b≠0时,g(x)为奇函数;
当a≠0且b=0时,g(x)为偶函数;
当a=0且b=0时,g(x)既是奇函数又是偶函数.
21世纪教育网(www.21cnjy.com)
3.3幂函数
知识点 幂函数
1.幂函数的概念
一般地,函数 叫做幂函数,其中x是自变量,α是常数.
2.五个幂函数的图象与性质
解析式 y=x y=x2 y=x3 y=x y=
图象
定义域 R R R
解析式 y=x y=x2 y=x3 y=x y=
值域 R R
奇偶性 奇函数 偶函数 奇函数 非奇非偶函数 奇函数
单调性 在(-∞,+∞)上单调递增 在(-∞,0]上单调递减,在(0,+∞)上单调递增 在(-∞,+∞)上单调递增 在[0,+∞)上单调递增 在(-∞,0)上单调递减,在(0,+∞)上单调递减
定点 (1,1)
【思考】
通过5个幂函数图象的观察,哪个象限一定有幂函数的图象?哪个象限一定没有幂函数的图象?
【提示】
第一象限一定有幂函数的图象,第四象限一定没有幂函数的图象
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)幂函数的图象必过点(0,0)和(1,1). ( )
(2)幂函数的图象都不过第二、四象限. ( )
(3)当幂指数α取1,3,时,幂函数y=xα是增函数. ( )
(4)若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大. ( )
【答案】(1)×(2)×(3)√(4)×
2.已知幂函数的图象过点(2,4),则其解析式为( )
A.y=x+2 B.y=x2 C.y= D.y=x3
【答案】B
【解析】设幂函数的解析式为y=xα,当x=2时,y=4,故2α=4,即α=2.
3.在下列四个图形中, 的大致图象是 ( )
【答案】D
【解析】函数的定义域为(0,+∞),是减函数.故选D.
4.已知f(x)=(m-1)x是幂函数,则m=________.
【解析】2
【解析】∵函数f(x)=(m-1)x是幂函数,∴m-1=1,即m=2.
5.已知幂函数f(x)=xα图象过点,则f(4)=________.
【答案】
【解析】∵幂函数f(x)=xα的图象过点,∴2α=,∴α=-.即f(x)=x,∴f(4)=4=.
题型一 幂函数的概念
【探究发现】
幂函数的解析式有什么特征
【提示】(1)指数为常数
(2)底数是自变量,自变量的系数为1,
(3)幂的系数为1
(4)只有1项
【学透用活】
【例1】 (1)下列函数:
①y=x3;②y=x;
③y=4x2;④y=x5+1;
⑤y=(x-1)2;⑥y=x;⑦y=ax(a>1).
其中幂函数的个数为 ( )
A.1 B.2 C.3 D.4
【答案】B
【解析】由幂函数的概念可知,只有是幂函数
(2) 若f(x)=(m2-4m-4)xm是幂函数,则m=________.
【答案】5或-1
【解析】(2)因为f(x)=(m2-4m-4)xm是幂函数,所以m2-4m-4=1,即m2-4m-5=0,解得m=5或m=-1.
【方法技巧】
求幂函数解析式的依据和常用方法
(1)依据:若一个函数为幂函数,则该函数应具备幂函数解析式所具备的特征,这是解决与幂函数有关问题的隐含条件.
(2)常用方法:设幂函数解析式为f(x)=xα,依据条件求出α.
【变式训练】
1.在函数y=,y=2x3,y=x2+x,y=1中,幂函数的个数为 ( )
A.0 B.1 C.2 D.3
【解析】因为y==x-2,所以是幂函数;y=2x3由于出现系数2,因此不是幂函数;y=x2+x是两项和的形式,不是幂函数;y=1=x0(x≠0),可以看出,常数函数y=1 的图象比幂函数y=x0的图象多了一个点(0,1),所以常数函数y=1不是幂函数.
2.已知幂函数f(x)=(m2-4m+4)x在(0,+∞)为增函数,则m的值为 ( ) A.1或3 B.3 C.2 D.1
【答案】D
【解析】由函数f(x)为幂函数,得m2-4m+4=1,解得m=1或m=3.
又幂函数f(x)单调递增,则m2-6m+8>0,据此可得,m=1.
题型二 幂函数的图象及应用
【学透用活】
(1)幂函数y=xα在第一象限内的图象特征:
①当α>1时,图象过点(1,1),下凸递增,如y=x3;
②当0<α<1时,图象过点(1,1),上凸递增,如y=x;
③当α<0时,图象过点(1,1),下凸递减,且向两坐标轴无限地逼近,如y=x-1.
(2)幂函数在第一象限内指数的变化规律:
在第一象限内直线x=1的右侧,图象从上到下,相应的指数由大变小;在直线x=1的左侧,图象从下到上,相应的指数由大变小.
(3)幂函数的图象一定会出现在第一象限内,一定不会出现在第四象限内,至于是否出现在第二、三象限内,要看函数的奇偶性;幂函数的图象最多只能同时出现在两个象限内;如果幂函数的图象与坐标轴相交,则交点一定是原点.
【例2】若点(,2)在幂函数f(x)的图象上,点在幂函数g(x)的图象上,问当x为何值时,(1)f(x)>g(x);(2)f(x)=g(x);(3)f(x)<g(x).
【解析】设f(x)=xα,因为点(,2)在幂函数f(x)的图象上,所以将点(,2)代入f(x)=xα中,得2=()α,解得α=2,则f(x)=x2.同理可求得g(x)=x-2.
在同一坐标系中作出函数f(x)=x2和g(x)=x-2的图象(如图所示),观察图象可得:
(1)当x>1或x<-1时,f(x)>g(x);
(2)当x=1或x=-1时,f(x)=g(x);
(3)当-1<x<1且x≠0时,f(x)<g(x).
【方法技巧】
解决幂函数图象问题的原则
(1)依据图象高低判断幂指数大小,相关结论为:在(0,1)上,指数越大,幂函数图象越靠近x轴(简记为指大图低);在(1,+∞)上,指数越大,幂函数图象越远离x轴(简记为指大图高).
(2)当α>0时,幂函数的图象都经过(0,0)和(1,1)点,在第一象限内,当0<α<1时,曲线上凸;当α>1时,曲线下凸;当α<0时,幂函数的图象都经过(1,1)点,在第一象限内,曲线下凸.
【变式训练】
1.函数y=x-1的图象关于x轴对称的图象大致是 ( )
【答案】B
【解析】y=x的图象位于第一象限且为增函数,所以函数图象是上升的,函数y=x-1的图象可看作由y=x的图象向下平移一个单位得到的(如选项A中的图所示),将y=x-1的图象关于x轴对称后即为选项B.
2.若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图所示,则a,b,c,d的大小关系是 ( )
A.d>c>b>a B.a>b>c>d
C.d>c>a>b D.a>b>d>c
【答案】B
【解析】令a=2,b=,c=-,d=-1,正好和题目所给的形式相符合.在
第一象限内,x=1的右侧部分的图象,图象由下至上,幂指数增大,所
以a>b>c>d.故选B.
题型三 利用幂函数的单调性比较大小
【探究发现】
幂函数的单调性如何判断?
【提示】(1)幂函数y=xa 的单调性主要通过a的正负判断,并且在第一象限内单调性的规律体现的比较明显.
(2)a>0时,幂函数y=xa在第一象限内单调递增;a<0 时,幂函数y=xa在第一象限内单调递减.
【学透用活】
【例3】比较下列各组数中两个数的大小.
(1)0.5与0.5;
(2)-1与-1;
(3) 与.
【解析】(1)∵幂函数y=x0.5在(0,+∞)上是单调递增的,又>,∴0.5>0.5.
(2)∵幂函数y=x-1在(-∞,0)上是单调递减的,
又-<-,∴-1>-1.
(3)∵函数y1=x为(0,+∞)上的增函数,又>1,∴>1=1.
又∵函数y2=x在(0,+∞)上是增函数,且<1,∴<1=1,∴>.
【方法技巧】
1.比较幂的大小的三种基本方法
直接法 当幂指数相同时,可直接利用幂函数的单调性来比较
转化法 当幂指数不同时,可以先转化为相同幂指数,再运用单调性比较大小
中间量法 当底数不同且幂指数也不同时,不能运用单调性比较大小,可选取适当的中间值,从而达到比较大小的目的
2.利用幂函数单调性比较大小时的注意点
比较大小的实数必须在同一函数的同一单调区间内,否则无法比较大小.
【变式训练】
1. (多选)下列不等式在a<b<0的条件下能成立的是( )
A.a-1>b-1 B.a<b C.b2<a2 D.a>b
【答案】ABC
【解析】分别构造函数y=x-1,y=x,y=x2,y=x,其中函数y=x-1,y=x2在(-∞,0)上为减函数,
故A、C成立.而y=x,y=x为(-∞,0)上的增函数,从而B成立,D不成立.
2.比较下列各题中两个幂的值的大小:
(1)1.1,0.9;
(2)3,.
【解析】(1)因为y=x为(0,+∞)上的减函数,又1.1>0.9,所以1.1<0.9.
(2)因为3=,函数y=x为[0,+∞)上的增函数,且<,所以<,即3<.
题型四 幂函数性质的综合应用
【学透用活】
已知函数f(x)=x(m∈N*).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若该函数图象经过点(2,),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
【解析】(1)∵m2+m=m(m+1),m∈N*,
∴m与m+1中必定有一个为偶数,
∴该函数的定义域为[0,+∞),
由幂函数的性质知,该函数在定义域上单调递增.
(2)∵该函数图象过点(2,),∴2=,
∴m2+m=2,∴m=1(m∈N*).
由f(2-a)>f(a-1),得解得1≤a<.
故m的值为1,满足条件f(2-a)>f(a-1)的实数a的取值范围为.
【方法技巧】
解决幂函数的综合问题,应注意以下两点:
(1)充分利用幂函数的图象、性质解题,如图象所过定点、单调性、奇偶性等;
(2)注意运用常见的思想方法解题,如分类讨论思想、数形结合思想.
【变式训练】
已知幂函数f(x)=(m2-5m+7)x-m-1(m∈R)为偶函数.
(1)求f的值;
(2)若f(2a+1)=f(a),求实数a的值.
【解析】(1)函数f(x)=(m2-5m+7)x-m-1(m∈R)为幂函数,
∴m2-5m+7=1,解得m=2或m=3.
当m=2时,f(x)=x-3,不是偶函数,舍去;
当m=3时,f(x)=x-4,为偶函数,满足题意.
∴f(x)=x-4,∴f=-4==16.
(2)由f(2a+1)=f(a),可得(2a+1)-4=a-4,
即解得a=-1或a=-.
【课堂思维激活】
一、综合性——强调融会贯通
1.已知函数f(x)=(m2+m-1)xm是幂函数,且在(0,+∞)上是减函数.
(1)求实数m的值;
(2)请画出f(x)的大致图象;
(3)若f(2a-1)>f(a),a∈R成立,求a的取值范围.
【解析】(1)由函数f(x)是幂函数,
则m2+m-1=1,解得m=-2或m=1,
又因为f(x)在(0,+∞)上是减函数,
所以m=-2.
(2)由(1)知,f(x)=x-2,
则f(x)的大致图象如图所示:
(3)由(2)知,f(x)的图象关于y轴对称,且在(0,+∞)上递减,
则由f(2a-1)>f(a),得|2a-1|<|a|,
即(2a-1)2<a2,可得(a-1)(3a-1)<0,解得<a<1,又a≠,
∴a的取值范围为∪.
二、应用性——强调学以致用
2.为了保证信息的安全传输须使用加密方式,有一种方式其加密、解密原理为:发送方由明文到密文(加密),
接收方由密文到明文(解密).现在加密密钥为y=xα(α为常数),如“4”通过加密后得到密文“2”.若接收方接
到密文“3”,则解密后得到的明文是什么?
【解析】由题目可知加密密钥y=xα(α是常数)是一个幂函数模型,所以
要想求得解密后得到的明文,就必须先求出α的值.由题意得2=4α,解
得α=,则y=x.由x=3,得x=9.即解密后得到的明文是9.
三、创新性——强调创新意识和创新思维
3.已知幂函数y=xα的图象经过点A(0,0),B(1,1),C(-1,1),D(4,2)中的三点,写出满足条件的一个α值.
【解析】当α=2时,y=x2经过A,B,C三点.
当α=时,y=x经过A,B,D三点,答案不唯一.
1.如图给出四个幂函数的图象,则图象与函数大致对应的是( )
A.①y=x;②y=x2;③y=x3;④y=x-1
B.①y=x3;②y=x;③y=x2;④y=x-1
C.①y=x2;②y=x3;③y=x;④y=x-1
D.①y=x3;②y=x2;③y=x;④y=x-1
【答案】D
【解析】y=x3是奇函数,且在R上递增,对应题图①;y=x2是偶函数,对应题图②;y=x的定义域为[0,+∞),对应题图③;y=x-1的定义域为(-∞,0)∪(0,+∞),对应题图④.故选D.
2.已知幂函数f(x)=(2n2-n)xn+1,若f(x)在其定义域上为增函数,则n等于( )
A.1或- B.1
C.- D.-1或
【答案】C
【解析】依题意得2n2-n=1,即2n2-n-1=0,解得n=1或n=-.
当n=1时,f(x)=x2,在R上不是增函数,不符合题意,舍去;
当n=-时,f(x)=x=,在定义域[0,+∞)上是增函数,符合题意.故选C.
3.如图所示,曲线C1与C2分别是函数y=xm和y=xn在第一象限内的图象,则下列结论正确的是( )
A.n
【答案】A
【解析】由图象可知,两函数在第一象限内递减,故m<0,n<0.当x=2时,2m>2n,所以n<m<0.
4.有四个幂函数:①f(x)=x-1;②f(x)=x-2;③f(x)=x3;④f(x)=x.某同学研究了其中的一个函数,他给出这个函数的三个性质:(1)偶函数;(2)值域是{y|y∈R,且y≠0};(3)在(-∞,0)上是增函数.如果他给出的三个性质中,有两个正确,一个错误,则他研究的函数是( )
A.① B.②
C.③ D.④
【答案】B
【解析】①f(x)=x-1只满足值域是{y|y∈R,且y≠0};③f(x)=x3只满足在(-∞,0)上是增函数;④f(x)=x只满足在(-∞,0)上是增函数,②f(x)=x-2是偶函数,在(-∞,0)上是增函数,但其值域是{y|y>0}.故选B.
5.已知幂函数f(x)=xa的图象过点,则函数g(x)=(x-2)f(x)在区间上的最小值是( )
A.-1 B.-2
C.-3 D.-4
【答案】C
【解析】由已知得2a=,解得a=-1,∴g(x)==1-在区间上单调递增,则g(x)min=g=-3.故选C.
6.已知幂函数f(x)=xα的部分对应值如表:
x 1
f(x) 1
则f(x)的单调递增区间是________.
【答案】 [0,+∞)
【解析】因为f =,所以α=,即α=,所以f(x)=x的单调递增区间是[0,+∞).
7.设α∈,则使f(x)=xα为奇函数且在(0,+∞)上单调递减的α的值是________.
【答案】-1
【解析】因为f(x)=xα为奇函数,所以α=-1,1,3.又因为f(x)在(0,+∞)上为减函数,所以α=-1.
8.若f(x)是幂函数,且满足=4,则f=________.
【答案】
【解析】设f(x)=xα,则f(4)=4α=22α,f(2)=2α.
∵==2α=4=22,
∴α=2,∴f(x)=x2,∴f =2=.
9.已知函数f(x)=(m2+2m)·xm2+m-1,m为何值时,函数f(x)是:(1)正比例函数;(2)反比例函数;(3)幂函数.
【解析】(1)若函数f(x)为正比例函数,则
∴m=1.
(2)若函数f(x)为反比例函数,则
∴m=-1.
(3)若函数f(x)为幂函数,则m2+2m=1,
∴m=-1±.
10.比较下列各组数的大小:
(1)3-和3.2-;
(2)和;
(3)4.1和3.8.
【解析】(1)函数y=x-在(0,+∞)上为减函数,又3<3.2,所以3->3.2-.
(2)=,=,函数y=x在(0,+∞)上为增函数,而>,所以>.
(3)4.1>1=1,0<3.8<1=1,
所以4.1>3.8.
11.幂函数y=xα(α≠0),当α取不同的正数时,在区间[0,1]上它们的图象是一簇曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xm,y=xn的图象三等分,即有BM=MN=NA,则mn等于( )
A.1 B.2
C.3 D.无法确定
【答案】A
【解析】由条件知,M,N,∴=m,=n,∴mn=n=n=,∴mn=1.故选A.
12.(多选)已知实数a,b满足等式a=b,则下列关系式中可能成立的是( )
A.0
【解析】画出y=x与y=x的图象(如图),设a=b=m,作直线y=m.
从图象知,若m=0或1,则a=b;若0
【答案】③
【解析】设f(x)=xα,则f(m+n)=(m+n)α,f(m)+f(n)=mα+nα,f(m)·f(n)=mα·nα=(mn)α,f(mn)=(mn)α,所以f(mn)=f(m)·f(n)一定成立,其他三个不一定成立,故填③.
14.已知幂函数f(x)= (m∈N*).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若函数f(x)的图象经过点(2,),试确定m的值,并求满足f(2-a)>f(a-1)的实数a的取值范围.
【解析】(1)∵m∈N*,
∴m2+m=m×(m+1)为偶数.
令m2+m=2k,k∈N*,则f(x)=,
∴f(x)的定义域为[0,+∞),且f(x)在[0,+∞)上为增函数.
(2)由题意可得=2=2,∴m2+m=2,解得m=1或m=-2(舍去),
∴f(x)=x.
由(1)知f(x)在定义域[0,+∞)上为增函数,
∴f(2-a)>f(a-1)等价于2-a>a-1≥0,解得1≤a<,故实数a的取值范围为.
15.已知幂函数f(x)=x (m-2)(m∈N)是偶函数,且在(0,+∞)上是减函数,求函数f(x)的解析式,并讨论g(x)=a-的奇偶性.
【解析】由f(x)=x (m-2)(m∈N)在(0,+∞)上是减函数,得(m-2)<0,∴m<2.
∵m∈N,∴m=0,1.∵f(x)是偶函数,∴只有当m=0时符合题意,故f(x)=x.
于是g(x)=-,g(-x)=+,且g(x)的定义域为(-∞,0)∪(0,+∞),关于原点对称.
当a≠0且b≠0时,g(x)既不是奇函数也不是偶函数;
当a=0且b≠0时,g(x)为奇函数;
当a≠0且b=0时,g(x)为偶函数;
当a=0且b=0时,g(x)既是奇函数又是偶函数.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
