湘教版初中数学七年级上册3.4一元一次方程模型的应用--行程问题 课件(共34张PPT)
文档属性
| 名称 | 湘教版初中数学七年级上册3.4一元一次方程模型的应用--行程问题 课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-25 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
速度、路程、时间之间的关系
路程=
时间=
速度=
速度×时间
路程÷速度
路程÷时间
复习回顾
填一填
甲、乙两地相距10千米,
如果小陈每小时走5千米,则需______小时走完.
如果小邱x小时走完,则他每小时走____千米.
2
探究新知1
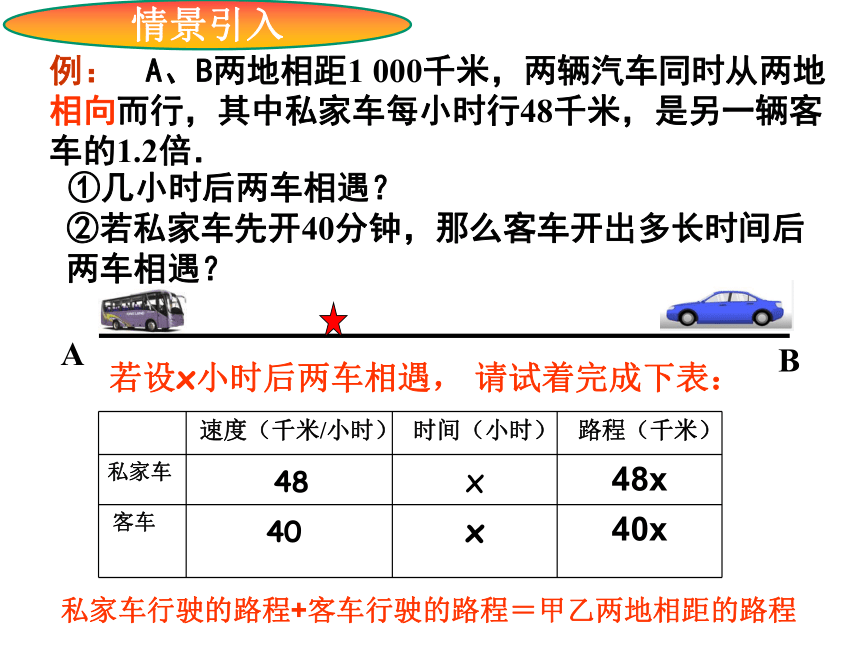
例: A、B两地相距1 000千米,两辆汽车同时从两地相向而行,其中私家车每小时行48千米,是另一辆客车的1.2倍.
②若私家车先开40分钟,那么客车开出多长时间后两车相遇?
①几小时后两车相遇?
A
B
私家车行驶的路程+客车行驶的路程=甲乙两地相距的路程
速度(千米/小时) 时间(小时) 路程(千米)
私家车 x 48x
客车 x
40x
若设x小时后两车相遇, 请试着完成下表:
48
40
情景引入
甲
乙
私家车行驶的路程+客车行驶的路程=甲乙两地相距的路程
速度(千米/小时) 时间(小时) 路程(千米)
私家车
客车 x 40x
48
40
若设客车开出x小时后两车相遇, 请试着完成下表:
例1 A、B两地相距1 000千米,两辆汽车同时从两地相向而行,其中私家车每小时行48千米,是另一辆客车的1.2倍.
①几小时后两车相遇?
②若私家车先开40分钟,那么客车开出多长时间后两车相遇?
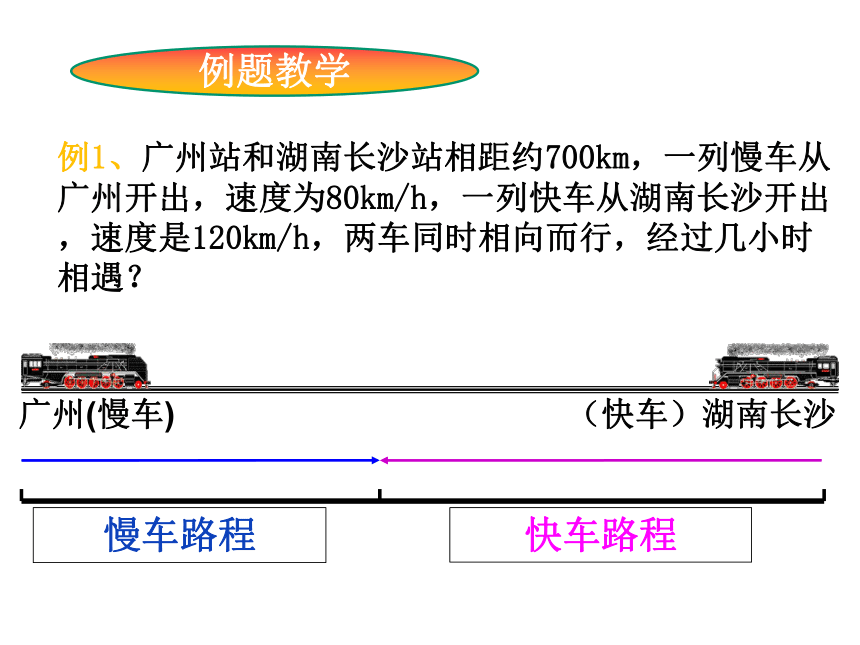
例1、广州站和湖南长沙站相距约700km,一列慢车从广州开出,速度为80km/h,一列快车从湖南长沙开出,速度是120km/h,两车同时相向而行,经过几小时相遇?
广州(慢车)
(快车)湖南长沙
慢车路程
快车路程
例题教学
解:设快车和慢车x h后相遇,则
80x+120x=700
解得:x=3.5
答:快车和慢车3.5小时后相遇.
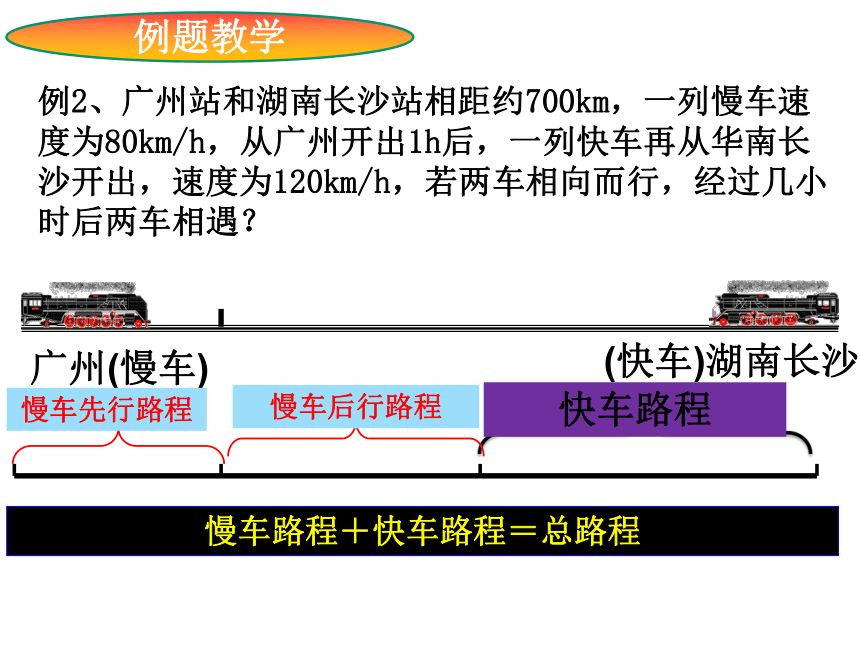
例2、广州站和湖南长沙站相距约700km,一列慢车速度为80km/h,从广州开出1h后,一列快车再从华南长沙开出,速度为120km/h,若两车相向而行,经过几小时后两车相遇?
广州(慢车)
(快车)湖南长沙
慢车先行路程
快车路程
慢车路程+快车路程=总路程
慢车后行路程
例题教学
解:设快车和慢车t h后相遇,则
80×1+80t+120t=700
解得:t=3.1
答:快车和慢车3.1小时后相遇.
张三、李四两人在500米长的环形跑道上,同时同地反向出发练习跑步,已知张三比李四速度快2m/s,若经过50s他们首次相遇,你能知道他们各自的速度吗?
等量关系
张三行的路程+李四行的路程=500米
学以致用
解:设李四的速度为x m/s,则张三的速度是 (x+2)m/s.
50x+50(x+2)=500
解得:x=4
张三的速度:4+2=6
答:张三的速度是6m/s,李四的速度是4m/s
例.甲、乙两列火车的长为144m和180m,甲车比乙车每秒多行4m.两列火车相向而行,从相遇到全部错开需9s,问两车的速度各是多少?
解:设乙车的速度是x m/s,
则甲车的速度是 m/s.
(x+4)
9x+9(x+4)=144+180
解得:x=16
答:甲的速度是20km/h,乙的速度是16km/h
则甲车速度:16+4=20
拓展延伸
行程问题——相遇问题
等量关系:
甲走的路程+乙走的路程=AB两地间的距离
归纳总结
探究新知2
例 A、B两站间的路程为448千米,一列快车从A站出发,每小时行驶80千米,一列慢车从B站出发,每小时行驶60千米,问:两车同时、同向而行,如果慢车在前,出发后多长时间快车追上慢车?
画图分析
c
A
B
快车行驶路程
慢车行驶路程
情景引入
分析:此题属于追及问题,等量关系为:
快车行驶路程—慢车行驶路程= A、B两站间的距离
(1)解:设黑色马t秒钟追上白色马,依题意得: 6t+ 10 =7t
解得 t=10
答:黑色马10秒钟可以追上白色马。
例1、两匹马赛跑,如果白色马的起点在黑色马起点前方10m处,白色马的速度是6m/s,黑色马的速度是7m/s,同时起跑,黑色马需要几秒才能追上白色马?
例题教学
例2、两匹马赛跑,白色马的速度是6m/s,黑色马的速度是7m/s,如果让白马先跑5s,黑色马再开始跑,几秒后可以追上白色马?
黑色马路程
30m
=
+黑色马后跑路程
白色马先跑路程
例题教学
例2、两匹马赛跑,白色马的速度是6m/s,黑色马的速度是7m/s,如果让白马先跑5s,黑色马再开始跑,几秒后可以追上白色马?
(2)解:设黑色马t秒钟追上白色马,依题意得: 6t+ 5×6 =7t
解得 t=30
答:黑色马30秒钟可以追上白色马。
例题教学
周一强强起得很早,6点钟便从家里出发,但他走了半个小时后,哥哥发现他的作业没有带,便骑车去送作业。学校要求7:20到校。
猜猜他能送到吗?
学以致用
若强强以每小时3千米的速度行驶,但他走了半个小时后,哥哥骑车以每小时6千米速度追赶,并且在途中追上了他,哥哥追上强强需要多长时间?
任务:
已知量、未知量是什么?
等量关系是什么?
如何设未知数 如何列方程?
【分析】
1.画线段图:
强强
哥哥
追击处
强强先走的路程
强强后走的路程
哥哥走的路程
强强走的路程=哥哥走的路程
2.等量关系是____________
设哥哥经过x小时追上强强
3.填表:
速度(km/h) 时间(h) 路程(km)
强强
哥哥 6
3
X+0.5
x
3(x+0.5)
6x
根据题意列方程得:3(X + 0.5)= 6X
解得:X=0.5
答:哥哥经过0.5小时追上强强
李三要到郊外训练警犬.他从基地以200米/分钟的速度跑了10分钟后,他的警犬再从基地按原路追去,警犬的速度是700米/分钟.
设警犬x分钟可追上小明,
则可列方程为 : ;
700x =200(10+x)
警犬行驶的路程=李三行驶的路程
拓展延伸
常见的追及问题及其等量关系:
同地不同时出发:
前者走的路程=追者走的路程
追者走的路程
前者先走
前者后走
追上
同时不同地出发:
前者的路程+两地间隔的路程=追者的路程
甲
追上
乙
追者
间隔
前者
归纳总结
探究新知3
例:若两人在800米的环形跑道上跑步,同时同地反向出发,求第一次相遇时间?(小红速度5m/s ,小绿速度6m/s)
情景引入
小云
小霞
例、如图:小云、小霞分别在400米环形跑道上练习跑步与竞走,小云每分钟跑220米,小霞每分钟走120米,两人同时由同一点同向出发,问几分钟后,小霞与小云第一次相遇?
若设x分钟后,小霞与小云第一次相遇,请试着完成下表:
速度(米/分钟) 时间(分钟) 路程(米)
小霞 x
小云
120
220
例题教学
x
120x
220x
小云跑的路程―小霞走的路程=环形跑道一周的长
根据题意列方程得:220x-120x=400
解得:x=4
答:4分钟后,小霞与小云第一次相遇
小组讨论:
两人同时由同一点同向出发,几分钟后,小霞与小云第二次相遇?第三次相遇?第n次相遇?(其他条件不变)
变式训练:如下图:小云、小霞分别在400米环形跑道上练习跑步与竞走,小云每分钟跑220米,小霞每分钟走120米,两人同时由同一点反向出发,问几分钟后,小云与小霞第一次相遇?
小云
小霞
等量关系:
解:设x分钟后,小霞与小云第一次相遇.
根据题意列方程得:
220x+120x=400
解得:x=
答: 分钟后,小云与小霞第一次相遇。
小云跑的路程 + 小霞走的路程 = 环形跑道一周的长
今天我们学习了哪些知识?
行程问题
特例:环形跑道问题
(1)相遇问题:
(2)追及问题:
甲走的路程+乙走的路程=AB两地间的距离
快者的路程—慢者的路程 = 二者之间的距离
同向出发:
反向出发:
追及问题
相遇问题
速度、路程、时间之间的关系
路程=
时间=
速度=
速度×时间
路程÷速度
路程÷时间
复习回顾
填一填
甲、乙两地相距10千米,
如果小陈每小时走5千米,则需______小时走完.
如果小邱x小时走完,则他每小时走____千米.
2
探究新知1
例: A、B两地相距1 000千米,两辆汽车同时从两地相向而行,其中私家车每小时行48千米,是另一辆客车的1.2倍.
②若私家车先开40分钟,那么客车开出多长时间后两车相遇?
①几小时后两车相遇?
A
B
私家车行驶的路程+客车行驶的路程=甲乙两地相距的路程
速度(千米/小时) 时间(小时) 路程(千米)
私家车 x 48x
客车 x
40x
若设x小时后两车相遇, 请试着完成下表:
48
40
情景引入
甲
乙
私家车行驶的路程+客车行驶的路程=甲乙两地相距的路程
速度(千米/小时) 时间(小时) 路程(千米)
私家车
客车 x 40x
48
40
若设客车开出x小时后两车相遇, 请试着完成下表:
例1 A、B两地相距1 000千米,两辆汽车同时从两地相向而行,其中私家车每小时行48千米,是另一辆客车的1.2倍.
①几小时后两车相遇?
②若私家车先开40分钟,那么客车开出多长时间后两车相遇?
例1、广州站和湖南长沙站相距约700km,一列慢车从广州开出,速度为80km/h,一列快车从湖南长沙开出,速度是120km/h,两车同时相向而行,经过几小时相遇?
广州(慢车)
(快车)湖南长沙
慢车路程
快车路程
例题教学
解:设快车和慢车x h后相遇,则
80x+120x=700
解得:x=3.5
答:快车和慢车3.5小时后相遇.
例2、广州站和湖南长沙站相距约700km,一列慢车速度为80km/h,从广州开出1h后,一列快车再从华南长沙开出,速度为120km/h,若两车相向而行,经过几小时后两车相遇?
广州(慢车)
(快车)湖南长沙
慢车先行路程
快车路程
慢车路程+快车路程=总路程
慢车后行路程
例题教学
解:设快车和慢车t h后相遇,则
80×1+80t+120t=700
解得:t=3.1
答:快车和慢车3.1小时后相遇.
张三、李四两人在500米长的环形跑道上,同时同地反向出发练习跑步,已知张三比李四速度快2m/s,若经过50s他们首次相遇,你能知道他们各自的速度吗?
等量关系
张三行的路程+李四行的路程=500米
学以致用
解:设李四的速度为x m/s,则张三的速度是 (x+2)m/s.
50x+50(x+2)=500
解得:x=4
张三的速度:4+2=6
答:张三的速度是6m/s,李四的速度是4m/s
例.甲、乙两列火车的长为144m和180m,甲车比乙车每秒多行4m.两列火车相向而行,从相遇到全部错开需9s,问两车的速度各是多少?
解:设乙车的速度是x m/s,
则甲车的速度是 m/s.
(x+4)
9x+9(x+4)=144+180
解得:x=16
答:甲的速度是20km/h,乙的速度是16km/h
则甲车速度:16+4=20
拓展延伸
行程问题——相遇问题
等量关系:
甲走的路程+乙走的路程=AB两地间的距离
归纳总结
探究新知2
例 A、B两站间的路程为448千米,一列快车从A站出发,每小时行驶80千米,一列慢车从B站出发,每小时行驶60千米,问:两车同时、同向而行,如果慢车在前,出发后多长时间快车追上慢车?
画图分析
c
A
B
快车行驶路程
慢车行驶路程
情景引入
分析:此题属于追及问题,等量关系为:
快车行驶路程—慢车行驶路程= A、B两站间的距离
(1)解:设黑色马t秒钟追上白色马,依题意得: 6t+ 10 =7t
解得 t=10
答:黑色马10秒钟可以追上白色马。
例1、两匹马赛跑,如果白色马的起点在黑色马起点前方10m处,白色马的速度是6m/s,黑色马的速度是7m/s,同时起跑,黑色马需要几秒才能追上白色马?
例题教学
例2、两匹马赛跑,白色马的速度是6m/s,黑色马的速度是7m/s,如果让白马先跑5s,黑色马再开始跑,几秒后可以追上白色马?
黑色马路程
30m
=
+黑色马后跑路程
白色马先跑路程
例题教学
例2、两匹马赛跑,白色马的速度是6m/s,黑色马的速度是7m/s,如果让白马先跑5s,黑色马再开始跑,几秒后可以追上白色马?
(2)解:设黑色马t秒钟追上白色马,依题意得: 6t+ 5×6 =7t
解得 t=30
答:黑色马30秒钟可以追上白色马。
例题教学
周一强强起得很早,6点钟便从家里出发,但他走了半个小时后,哥哥发现他的作业没有带,便骑车去送作业。学校要求7:20到校。
猜猜他能送到吗?
学以致用
若强强以每小时3千米的速度行驶,但他走了半个小时后,哥哥骑车以每小时6千米速度追赶,并且在途中追上了他,哥哥追上强强需要多长时间?
任务:
已知量、未知量是什么?
等量关系是什么?
如何设未知数 如何列方程?
【分析】
1.画线段图:
强强
哥哥
追击处
强强先走的路程
强强后走的路程
哥哥走的路程
强强走的路程=哥哥走的路程
2.等量关系是____________
设哥哥经过x小时追上强强
3.填表:
速度(km/h) 时间(h) 路程(km)
强强
哥哥 6
3
X+0.5
x
3(x+0.5)
6x
根据题意列方程得:3(X + 0.5)= 6X
解得:X=0.5
答:哥哥经过0.5小时追上强强
李三要到郊外训练警犬.他从基地以200米/分钟的速度跑了10分钟后,他的警犬再从基地按原路追去,警犬的速度是700米/分钟.
设警犬x分钟可追上小明,
则可列方程为 : ;
700x =200(10+x)
警犬行驶的路程=李三行驶的路程
拓展延伸
常见的追及问题及其等量关系:
同地不同时出发:
前者走的路程=追者走的路程
追者走的路程
前者先走
前者后走
追上
同时不同地出发:
前者的路程+两地间隔的路程=追者的路程
甲
追上
乙
追者
间隔
前者
归纳总结
探究新知3
例:若两人在800米的环形跑道上跑步,同时同地反向出发,求第一次相遇时间?(小红速度5m/s ,小绿速度6m/s)
情景引入
小云
小霞
例、如图:小云、小霞分别在400米环形跑道上练习跑步与竞走,小云每分钟跑220米,小霞每分钟走120米,两人同时由同一点同向出发,问几分钟后,小霞与小云第一次相遇?
若设x分钟后,小霞与小云第一次相遇,请试着完成下表:
速度(米/分钟) 时间(分钟) 路程(米)
小霞 x
小云
120
220
例题教学
x
120x
220x
小云跑的路程―小霞走的路程=环形跑道一周的长
根据题意列方程得:220x-120x=400
解得:x=4
答:4分钟后,小霞与小云第一次相遇
小组讨论:
两人同时由同一点同向出发,几分钟后,小霞与小云第二次相遇?第三次相遇?第n次相遇?(其他条件不变)
变式训练:如下图:小云、小霞分别在400米环形跑道上练习跑步与竞走,小云每分钟跑220米,小霞每分钟走120米,两人同时由同一点反向出发,问几分钟后,小云与小霞第一次相遇?
小云
小霞
等量关系:
解:设x分钟后,小霞与小云第一次相遇.
根据题意列方程得:
220x+120x=400
解得:x=
答: 分钟后,小云与小霞第一次相遇。
小云跑的路程 + 小霞走的路程 = 环形跑道一周的长
今天我们学习了哪些知识?
行程问题
特例:环形跑道问题
(1)相遇问题:
(2)追及问题:
甲走的路程+乙走的路程=AB两地间的距离
快者的路程—慢者的路程 = 二者之间的距离
同向出发:
反向出发:
追及问题
相遇问题
同课章节目录
