4.2.2指数函数图像和性质 课件(共25张PPT)
文档属性
| 名称 | 4.2.2指数函数图像和性质 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 10:21:38 | ||
图片预览







文档简介
(共25张PPT)
4.2.2指数函数的图像和性质
人教A(2019)版
必修一
新知导入
1、指数函数的概念
一般地,形如的函数 ,叫做指数函数,
其中x是自变量,a是不等于1的正的常数.
(1)幂的形式;
2、指数函数y=ax的基本特征
(2)幂的底数是一个大于0且不等于1的常数;
(3)幂的指数是一个变量.
接下来,我们用研究幂函数的思路来探讨指数函数的性质
3、研究幂函数的性质方法:
从图像入手,研究函数的定义域、值域、单调性等性质。
温故知新
新知讲解
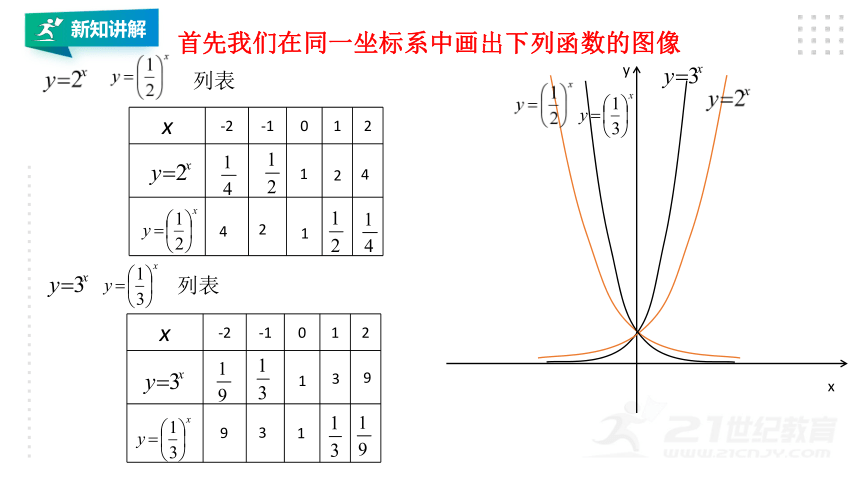
首先我们在同一坐标系中画出下列函数的图像
x -2 -1 0 1 2
x -2 -1 0 1 2
1
2
4
4
2
1
1
9
9
3
1
3
列表
x
y
列表
新知讲解
一、指数函数的图像与性质:
(1)图象全在x轴上方,与x轴无限接近;
(2)无论a取什么值,图象过定点(0,1)
(3)a>1时,自左向右图象逐渐上升;
0(4)
观察这四个函数图像我们发现:
新知讲解
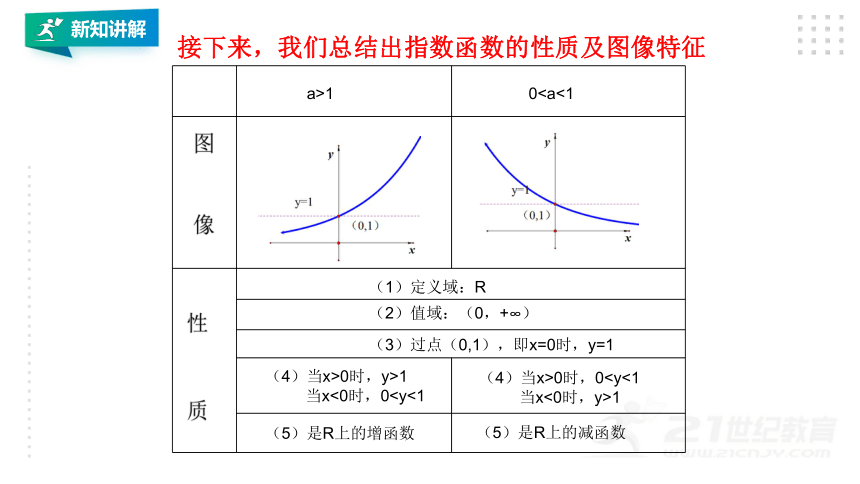
接下来,我们总结出指数函数的性质及图像特征
图 像
性 质
a>1
0(1)定义域:R
(2)值域:(0,+∞)
(3)过点(0,1),即x=0时,y=1
(5)是R上的增函数
(5)是R上的减函数
(4)当x>0时,y>1
当x<0时,0(4)当x>0时,0当x<0时,y>1
1、与指数函数相关的定义域
二、指数函数性质的简单应用
求下列函数的定义域
(1)y=
(2)y=
(3)y=
解:(1)函数有意义当且仅当x2-x-6≠0,解得x≠-2且x≠3,
所以函数的定义域为{x|x∈R,x≠-2且x≠3}.
(2)函数有意义当且仅当x2+2x-8≥0,解得x≤-4或x≥2,
所以函数的定义域为{x|x≤-4或x≥2}.
(3)函数有意义当且仅当2x-1-8≥0,即2x-1≥8,解得x≥4,
所以函数的定义域为[4,+∞).
合作探究
2、与指数函数相关的值域问题
(1)利用指数函数的单调性求值域:
例:y=2x,x∈(-1,4]
解:∵函数y=2x在R上单调递增,所以在x∈(-1,4]上单调递增,
∴ 2-1故函数y=2x,x∈(-1,4]的值域
合作探究
(2)形如y=af(x)类型函数的值域
例:求函数
的值域
解:
所以t≤
而
是R上的减函数
所以
所以函数
合作探究
(3)利用换元构造二次函数求值域
提醒:在构造二次函数求最值时,注意t的范围
总结:对于y=f[g(x)]我们称为复合函数,由y=f(u),u=g(x)复合而成
的函数,y=f(u)称为外函数,u=g(x)称为内函数,先求内函数的值域,再
利用外函数的图像和性质求值域.
合作探究
3、形如y=af(x)类型函数的单调性
例:求函数
的单调区间。
提示:复合函数单调性判断法则:“同增异减”,即内外函数的单
调性相同则为增函数,单调性相反则为减函数。
合作探究
4、比较大小
解:(1)考查指数函数y=1.7x,
由于底数1.7>1,所以指数函数y=1.7x在(-∞,+∞)上是增函数.
∵2.5<3,∴1.72.5<1.73.
(2)考查函数y=0.8x,由于0<0.8<1,
所以指数函数y=0.8x在(-∞,+∞)上为减函数.
∵-0.1>-0.2,∴0.8-0.1<0.8-0.2.
例1、利用单调性比较大小:
(1)1.72.5,1.73; (2)0.8-0.1,0.8-0.2;
合作探究
例2、利用中间值比较大小:
解:(1)由指数函数的性质得
1.70.3>1.70=1,
0.93.1<0.90=1,
∴1.70.3>0.93.1.
(2)底数不同、根指数也不同的两个数比较其大小,要化为同底数的
或化为同指数的再作比较
合作探究
5、解与指数函数相关的不等式
例:求不等式 <2-2x的解集。
解:因为 <2-2x,
所以
因为y= 在R上单调递减,
所以x2-3>2x,解得x>3或x<-1,
所以不等式的解集是{x|x>3或x<-1}
合作探究
6、与指数函数图像相关的问题
例1.函数f(x)=3-ax+1(a>0,且a≠1)的图象恒过定点 ( )
A.(-1,2) B.(1,2) C.(-1,1) D.(0,2)
【解析】依题意,由x+1=0得,x=-1,
将x=-1代入f(x)=3-ax+1得,f(-1)=3-a0=2,
所以函数f(x)=3-ax+1(a>0,且a≠1)的图象恒过定点(-1,2).选A.
A
合作探究
例2、判断下列指数函数底数大小:
y= ,y= ,y= ,y= ,如图,
试判断底数大小。
方法指导:由指数函数y=ax(a>0且a≠1)的图像与直线x=1相交于点(1,a)可知,在y轴右侧,图像从下到上相应的底数由小变大.
因此:上述函数底数的从小到大依次是:0合作探究
a4
a3
a2
a1
7、综合应用
例4 如图,某城市人口呈指数增长.(1)根据图象,估计该城市人口每
翻一番所需的时间 (倍增期);
(2)该城市人口从80万人开始,经过20年会增长到多少万人?
| | | | | | | |
10 20 30 40 50 60 70 80
| | | | | | | |
80 70 60 50 40 30 20 10
解:(1)观察图,发现该城市人口经过20年约为10万人,经过40年约为20万人,即由10万人口增加到20万人口所用的时间约为20年,所以该城市人口每翻一番所需的时间约为20年.
(2)因为倍增期为20年,所以每经过20年, 人口将翻一番.因此,从80万人开始,经过20年, 该城市人口大约会增长到160万人
合作探究
课堂练习
1.解不等式:
解:(1)由2x≥4x+1得,2x≥22(x+1)
因为y=2x为增函数,所以x≥2(x+1)
解得:x≤-2
(2)当a>1时,y=ax是R上的增函数,所以3x-1≤2x-4
解得:x≤-3,所以当a>1时不等式的解集为:(-∞,-3]
当0解得:x≥-3,所以当02.求函数 的值域
解:令t=x2-2x-3=(x-1)2-4≥-4, 是R上的减函数,所以 ,所以函数 的值域是
课堂练习
3.求函数f(x)=3·4x-2x(x≥0)的最小值.
解:f(x)=3·(2x)2-2x
令t=2x因为0≤x,所以t=2x≥1,
所以f(x)=3·(2x)2-2x可化为y=3t2-t, t≥1,
由二次函数图像和性质得到,y的最小值为2,
所以f(x)的最小值是2
课堂练习
4.比较下列各题中两个值的大小.
解: (1)∵y=0.3x为减函数,又x<x+1,∴0.3x>0.3x+1.
(2)化同底为: ,与 ,∵函数y=2x为增函数,2> .
∴22> ,即 .
(1) 0.3x与0.3x+1
课堂练习
5.求函数
的单调递减区间。
解:令t =x2-2x=(x-1)2-1,
则 单调递减,
利用二次函数的性质可得函数t的增区间为[1,+∞)
函数 的减区间是[1,+∞);
所以由复合函数单调性的判断
课堂总结
指数函数的
图象和性质
指数函数的图象
指数函数的性质
定义域、值域
过定点
单调性
应用指导
利用单调性比较大小时,注意0、1的灵活运用
解决过定点问题的关键是令函数解析式中的指数为0
函数y=af(x)与f(x)的定义域相同
板书设计
指数函数图像
指数函数性质
简单应用
(1)定义域:R
(2)值域:(0,+∞)
(3)过点(0,1),即x=0时,y=1
(4)a>1时,当x>0时,y>1
当x<0时,000时,0当x<0时,y>1
(5)a>1时,是R上的增函数
0作业布置
三.若 ,求实数a的取值范围。
一.填空题:
1.已知函数f(x)=ax(a>0且a≠1),的图象经过点(1,2),则f(2)的值是 ,a= .
2.已知函数f(x)=a2x+b (a>0且a≠1,b∈R),的图象恒过点(1,1),则b= .
3.已知函数f(x)=(a-1)x ,在R上为增函数,则a的取值范围是 .
二.若函数 的定义域为(-∞,0],求a的取值范围.
四.课本P118练习1、2,P119综合运用6、7
https://www.21cnjy.com/help/help_extract.php
4.2.2指数函数的图像和性质
人教A(2019)版
必修一
新知导入
1、指数函数的概念
一般地,形如的函数 ,叫做指数函数,
其中x是自变量,a是不等于1的正的常数.
(1)幂的形式;
2、指数函数y=ax的基本特征
(2)幂的底数是一个大于0且不等于1的常数;
(3)幂的指数是一个变量.
接下来,我们用研究幂函数的思路来探讨指数函数的性质
3、研究幂函数的性质方法:
从图像入手,研究函数的定义域、值域、单调性等性质。
温故知新
新知讲解
首先我们在同一坐标系中画出下列函数的图像
x -2 -1 0 1 2
x -2 -1 0 1 2
1
2
4
4
2
1
1
9
9
3
1
3
列表
x
y
列表
新知讲解
一、指数函数的图像与性质:
(1)图象全在x轴上方,与x轴无限接近;
(2)无论a取什么值,图象过定点(0,1)
(3)a>1时,自左向右图象逐渐上升;
0
观察这四个函数图像我们发现:
新知讲解
接下来,我们总结出指数函数的性质及图像特征
图 像
性 质
a>1
0
(2)值域:(0,+∞)
(3)过点(0,1),即x=0时,y=1
(5)是R上的增函数
(5)是R上的减函数
(4)当x>0时,y>1
当x<0时,0
1、与指数函数相关的定义域
二、指数函数性质的简单应用
求下列函数的定义域
(1)y=
(2)y=
(3)y=
解:(1)函数有意义当且仅当x2-x-6≠0,解得x≠-2且x≠3,
所以函数的定义域为{x|x∈R,x≠-2且x≠3}.
(2)函数有意义当且仅当x2+2x-8≥0,解得x≤-4或x≥2,
所以函数的定义域为{x|x≤-4或x≥2}.
(3)函数有意义当且仅当2x-1-8≥0,即2x-1≥8,解得x≥4,
所以函数的定义域为[4,+∞).
合作探究
2、与指数函数相关的值域问题
(1)利用指数函数的单调性求值域:
例:y=2x,x∈(-1,4]
解:∵函数y=2x在R上单调递增,所以在x∈(-1,4]上单调递增,
∴ 2-1
合作探究
(2)形如y=af(x)类型函数的值域
例:求函数
的值域
解:
所以t≤
而
是R上的减函数
所以
所以函数
合作探究
(3)利用换元构造二次函数求值域
提醒:在构造二次函数求最值时,注意t的范围
总结:对于y=f[g(x)]我们称为复合函数,由y=f(u),u=g(x)复合而成
的函数,y=f(u)称为外函数,u=g(x)称为内函数,先求内函数的值域,再
利用外函数的图像和性质求值域.
合作探究
3、形如y=af(x)类型函数的单调性
例:求函数
的单调区间。
提示:复合函数单调性判断法则:“同增异减”,即内外函数的单
调性相同则为增函数,单调性相反则为减函数。
合作探究
4、比较大小
解:(1)考查指数函数y=1.7x,
由于底数1.7>1,所以指数函数y=1.7x在(-∞,+∞)上是增函数.
∵2.5<3,∴1.72.5<1.73.
(2)考查函数y=0.8x,由于0<0.8<1,
所以指数函数y=0.8x在(-∞,+∞)上为减函数.
∵-0.1>-0.2,∴0.8-0.1<0.8-0.2.
例1、利用单调性比较大小:
(1)1.72.5,1.73; (2)0.8-0.1,0.8-0.2;
合作探究
例2、利用中间值比较大小:
解:(1)由指数函数的性质得
1.70.3>1.70=1,
0.93.1<0.90=1,
∴1.70.3>0.93.1.
(2)底数不同、根指数也不同的两个数比较其大小,要化为同底数的
或化为同指数的再作比较
合作探究
5、解与指数函数相关的不等式
例:求不等式 <2-2x的解集。
解:因为 <2-2x,
所以
因为y= 在R上单调递减,
所以x2-3>2x,解得x>3或x<-1,
所以不等式的解集是{x|x>3或x<-1}
合作探究
6、与指数函数图像相关的问题
例1.函数f(x)=3-ax+1(a>0,且a≠1)的图象恒过定点 ( )
A.(-1,2) B.(1,2) C.(-1,1) D.(0,2)
【解析】依题意,由x+1=0得,x=-1,
将x=-1代入f(x)=3-ax+1得,f(-1)=3-a0=2,
所以函数f(x)=3-ax+1(a>0,且a≠1)的图象恒过定点(-1,2).选A.
A
合作探究
例2、判断下列指数函数底数大小:
y= ,y= ,y= ,y= ,如图,
试判断底数大小。
方法指导:由指数函数y=ax(a>0且a≠1)的图像与直线x=1相交于点(1,a)可知,在y轴右侧,图像从下到上相应的底数由小变大.
因此:上述函数底数的从小到大依次是:0
a4
a3
a2
a1
7、综合应用
例4 如图,某城市人口呈指数增长.(1)根据图象,估计该城市人口每
翻一番所需的时间 (倍增期);
(2)该城市人口从80万人开始,经过20年会增长到多少万人?
| | | | | | | |
10 20 30 40 50 60 70 80
| | | | | | | |
80 70 60 50 40 30 20 10
解:(1)观察图,发现该城市人口经过20年约为10万人,经过40年约为20万人,即由10万人口增加到20万人口所用的时间约为20年,所以该城市人口每翻一番所需的时间约为20年.
(2)因为倍增期为20年,所以每经过20年, 人口将翻一番.因此,从80万人开始,经过20年, 该城市人口大约会增长到160万人
合作探究
课堂练习
1.解不等式:
解:(1)由2x≥4x+1得,2x≥22(x+1)
因为y=2x为增函数,所以x≥2(x+1)
解得:x≤-2
(2)当a>1时,y=ax是R上的增函数,所以3x-1≤2x-4
解得:x≤-3,所以当a>1时不等式的解集为:(-∞,-3]
当0
解:令t=x2-2x-3=(x-1)2-4≥-4, 是R上的减函数,所以 ,所以函数 的值域是
课堂练习
3.求函数f(x)=3·4x-2x(x≥0)的最小值.
解:f(x)=3·(2x)2-2x
令t=2x因为0≤x,所以t=2x≥1,
所以f(x)=3·(2x)2-2x可化为y=3t2-t, t≥1,
由二次函数图像和性质得到,y的最小值为2,
所以f(x)的最小值是2
课堂练习
4.比较下列各题中两个值的大小.
解: (1)∵y=0.3x为减函数,又x<x+1,∴0.3x>0.3x+1.
(2)化同底为: ,与 ,∵函数y=2x为增函数,2> .
∴22> ,即 .
(1) 0.3x与0.3x+1
课堂练习
5.求函数
的单调递减区间。
解:令t =x2-2x=(x-1)2-1,
则 单调递减,
利用二次函数的性质可得函数t的增区间为[1,+∞)
函数 的减区间是[1,+∞);
所以由复合函数单调性的判断
课堂总结
指数函数的
图象和性质
指数函数的图象
指数函数的性质
定义域、值域
过定点
单调性
应用指导
利用单调性比较大小时,注意0、1的灵活运用
解决过定点问题的关键是令函数解析式中的指数为0
函数y=af(x)与f(x)的定义域相同
板书设计
指数函数图像
指数函数性质
简单应用
(1)定义域:R
(2)值域:(0,+∞)
(3)过点(0,1),即x=0时,y=1
(4)a>1时,当x>0时,y>1
当x<0时,0
(5)a>1时,是R上的增函数
0
三.若 ,求实数a的取值范围。
一.填空题:
1.已知函数f(x)=ax(a>0且a≠1),的图象经过点(1,2),则f(2)的值是 ,a= .
2.已知函数f(x)=a2x+b (a>0且a≠1,b∈R),的图象恒过点(1,1),则b= .
3.已知函数f(x)=(a-1)x ,在R上为增函数,则a的取值范围是 .
二.若函数 的定义域为(-∞,0],求a的取值范围.
四.课本P118练习1、2,P119综合运用6、7
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
