2021-2022学年湘教版数学七年级上册 1.1 具有相反意义的量课件(共31张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学七年级上册 1.1 具有相反意义的量课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-25 20:42:53 | ||
图片预览











文档简介
(共31张PPT)
古代猎人打了一只老鹰,用数如何表示
一只老鹰——有了自然数
仔细观察周围的生活
二人分一只西瓜,用数如何表示半只
西瓜——有了分数
货币购物,用数如何表示2元
3角4分——有了小数。
那存入1000元,支出1000元又怎样用数字表示呢?
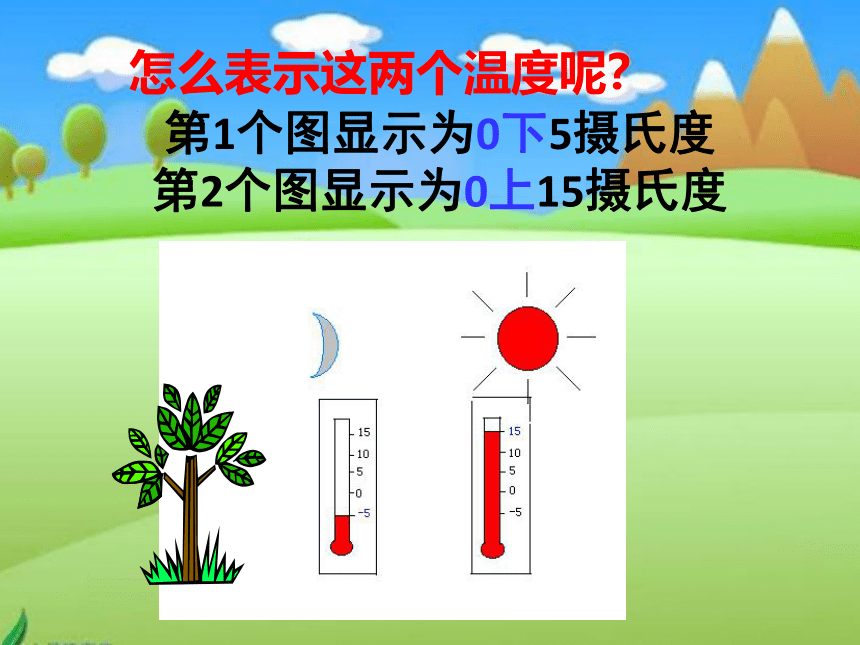
第1个图显示为0下5摄氏度
第2个图显示为0上15摄氏度
怎么表示这两个温度呢?
那存入1000元与支出1000元又怎样用数字表示呢?
那零上5摄氏度和零下15摄氏度怎么用数字表示呢?
第一章 有理数
§1.1具有相反意义的量
1、相反意义的量包含2个要素:
怎样理解具有相反意义的量?
前进8m与前进5m;上升与下降。
(2)是同类的量,具有数量(数量不一定相同),且带有单位。
(1)意义要相反;
2、与一个量成相反意义的量只有一个吗?
与上升2m成相反意义的量有哪些?
具有相反意义的量
收入 盈余 上升 零上 东 增加 存
支出 亏损 下降 零下 西 减少 取
日常生活中还有哪些相反意义量的词呢?
判断:
(1)前进和后退是两个具有相反意义的量.
(2)零上6℃的相反意义的量只有零下6℃。
(3)收入50万元和亏损20万元是两个具有相反意义的量。
(4)上涨100元和下降50点是两个具有相反意义的量。
×
×
×
×
如何用数字表示具有相反意义的量呢?
为了表示具有相反意义的量,我们把其中的一种意义的量用正数表示。正数前面可加上“+”号,(常省略)(课本举例)
把另一种与之意义相反的量用负数来表示,在正数前面加上“ ”(读作负)来表示,如 233, 60,-0.5等叫做负数
零既不是正数,也不是负数。
0是正负数的分界。
思考:0是正数还是负数呢?
那存入1000元,支出1000元又怎样表示呢?
存入和支出意义相反,存入1000元记作“+1000”,支出1000元记作“-1000”。
第1个图显示为0下5摄氏度
第2个图显示为0上15摄氏度
观察图形
哪位同学还能举出具有相反意义的量?并分别用正、负数来表示。
符号 具有相反意义的词
+ 收入 盈余 上升 零上 东 增加 存
- 支出 亏损 下降 零下 西 减少 取
“负”与“正”相对,增长-1就是减少1;增长-6.4%,是什么意思?什么情况下增长率是0?
增长-6.4%,就是减少6.4%
既没有增加又没有减少的情况下增长率为0
1、如果把收入50元,记作+50元,那么下列各数分别表示什么意义?
①30元;②-25元;③4.5元;④-72元
2、如果6摄氏度用60C表示,那么零下5摄氏度如何表示?
3、如果增加2%记作+2%,那么减少4%如何表示?增长-6%表示什么意义?
例题讲解
知识探究二、有理数的分类
为计数、排序、表示没有产生了自然数
为表示平分一个事物,产生了分数
为表示具有相反意义的量,产生了正数、和负数
小数和整数
16, 3, 10, 19, 1, 56, 132 ,
0
, , , 0.1, 37.8, 25%,
-16, -3, -10,-19, -1, -56, -132 ,
, , , -0.1, -37.8, -25% ,
正整数
负整数
零
正分数
负分数
整数
分数
…
…
…
…
正整数、零、和负整数统称整数.
正分数、负分数统称分数
有理数
有理数的分类
二
理解有理数的定义,观察下面演示:
负分数
正分数
负整数
正整数
零
整数
分数
有理数
负分数
正分数
负整数
正整数
零
整数
分数
有理数
按定义分:
由刚才的演示可知:
1.有理数可分为哪两类数
2.整数可分为哪几类
3.分数可分为哪几类
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
思考:如果按符号(正、负)来分类,又该怎样分呢?
例4 把下列各数填入表示它所在的数集的圈里:
典例精析
-18, , 3.1416, 0, 2017, ,-0.142857,95%.
…
…
…
…
正数集
负数集
整数集
有理数集
负数集
整数集
…
…
…
|
负整数集
-18,
0,2017,
,-0.142857,
思考:非负整数是指哪些数?非正整数呢?
正整数和零
-18, , 3.1416, 0, 2017, ,-0.142857,95%.
负整数和零
负分数
正分数
负整数
正整数
零
整数
分数
有理数
负分数
正分数
负整数
正整数
零
整数
分数
有理数
1.把下列各数分别填在相应集合的圈里:
正数集合{ …};
负数集合{ …};
非正整数集合{ …};
非负整数集合{ …}.
练一练
正数集合{ …};
负数集合{ …};
整数集合{ …};
正分数集合{ …};
负分数集合{ …};
分数集合{ …}.
有理数的分类中的四点注意:
1.相对性:正数是相对负数而言的,整数是相对分
数而言的.
2.特殊0:0既不是正数,也不是负数,但0是整数.
3.多属性:同一个数,可能属于多个不同的集合.如
5既是正数又是整数.
4.提醒:分数包括有限小数和无限循环小数.
归纳总结
1.具有相反意义的量应满足的条件:①意义相反;②同类的量(带有单位),数量不一定相等。
2.有理数的分类:
有理数
整数
分数
负整数
负分数
正分数
正整数
0
正有理数
负有理数
正分数
负分数
负整数
正整数
0
有理数
课堂小结
3.注意0的特殊性:0既不是正数,也不是负数.
正数和0统称为非负数.
课堂作业:习题1.1-1、2、3、4题(抄题目)
课后作业
课后作业:学法1.1
上交时间:下午上第一节课之前
晚自习第一节课前
古代猎人打了一只老鹰,用数如何表示
一只老鹰——有了自然数
仔细观察周围的生活
二人分一只西瓜,用数如何表示半只
西瓜——有了分数
货币购物,用数如何表示2元
3角4分——有了小数。
那存入1000元,支出1000元又怎样用数字表示呢?
第1个图显示为0下5摄氏度
第2个图显示为0上15摄氏度
怎么表示这两个温度呢?
那存入1000元与支出1000元又怎样用数字表示呢?
那零上5摄氏度和零下15摄氏度怎么用数字表示呢?
第一章 有理数
§1.1具有相反意义的量
1、相反意义的量包含2个要素:
怎样理解具有相反意义的量?
前进8m与前进5m;上升与下降。
(2)是同类的量,具有数量(数量不一定相同),且带有单位。
(1)意义要相反;
2、与一个量成相反意义的量只有一个吗?
与上升2m成相反意义的量有哪些?
具有相反意义的量
收入 盈余 上升 零上 东 增加 存
支出 亏损 下降 零下 西 减少 取
日常生活中还有哪些相反意义量的词呢?
判断:
(1)前进和后退是两个具有相反意义的量.
(2)零上6℃的相反意义的量只有零下6℃。
(3)收入50万元和亏损20万元是两个具有相反意义的量。
(4)上涨100元和下降50点是两个具有相反意义的量。
×
×
×
×
如何用数字表示具有相反意义的量呢?
为了表示具有相反意义的量,我们把其中的一种意义的量用正数表示。正数前面可加上“+”号,(常省略)(课本举例)
把另一种与之意义相反的量用负数来表示,在正数前面加上“ ”(读作负)来表示,如 233, 60,-0.5等叫做负数
零既不是正数,也不是负数。
0是正负数的分界。
思考:0是正数还是负数呢?
那存入1000元,支出1000元又怎样表示呢?
存入和支出意义相反,存入1000元记作“+1000”,支出1000元记作“-1000”。
第1个图显示为0下5摄氏度
第2个图显示为0上15摄氏度
观察图形
哪位同学还能举出具有相反意义的量?并分别用正、负数来表示。
符号 具有相反意义的词
+ 收入 盈余 上升 零上 东 增加 存
- 支出 亏损 下降 零下 西 减少 取
“负”与“正”相对,增长-1就是减少1;增长-6.4%,是什么意思?什么情况下增长率是0?
增长-6.4%,就是减少6.4%
既没有增加又没有减少的情况下增长率为0
1、如果把收入50元,记作+50元,那么下列各数分别表示什么意义?
①30元;②-25元;③4.5元;④-72元
2、如果6摄氏度用60C表示,那么零下5摄氏度如何表示?
3、如果增加2%记作+2%,那么减少4%如何表示?增长-6%表示什么意义?
例题讲解
知识探究二、有理数的分类
为计数、排序、表示没有产生了自然数
为表示平分一个事物,产生了分数
为表示具有相反意义的量,产生了正数、和负数
小数和整数
16, 3, 10, 19, 1, 56, 132 ,
0
, , , 0.1, 37.8, 25%,
-16, -3, -10,-19, -1, -56, -132 ,
, , , -0.1, -37.8, -25% ,
正整数
负整数
零
正分数
负分数
整数
分数
…
…
…
…
正整数、零、和负整数统称整数.
正分数、负分数统称分数
有理数
有理数的分类
二
理解有理数的定义,观察下面演示:
负分数
正分数
负整数
正整数
零
整数
分数
有理数
负分数
正分数
负整数
正整数
零
整数
分数
有理数
按定义分:
由刚才的演示可知:
1.有理数可分为哪两类数
2.整数可分为哪几类
3.分数可分为哪几类
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
思考:如果按符号(正、负)来分类,又该怎样分呢?
例4 把下列各数填入表示它所在的数集的圈里:
典例精析
-18, , 3.1416, 0, 2017, ,-0.142857,95%.
…
…
…
…
正数集
负数集
整数集
有理数集
负数集
整数集
…
…
…
|
负整数集
-18,
0,2017,
,-0.142857,
思考:非负整数是指哪些数?非正整数呢?
正整数和零
-18, , 3.1416, 0, 2017, ,-0.142857,95%.
负整数和零
负分数
正分数
负整数
正整数
零
整数
分数
有理数
负分数
正分数
负整数
正整数
零
整数
分数
有理数
1.把下列各数分别填在相应集合的圈里:
正数集合{ …};
负数集合{ …};
非正整数集合{ …};
非负整数集合{ …}.
练一练
正数集合{ …};
负数集合{ …};
整数集合{ …};
正分数集合{ …};
负分数集合{ …};
分数集合{ …}.
有理数的分类中的四点注意:
1.相对性:正数是相对负数而言的,整数是相对分
数而言的.
2.特殊0:0既不是正数,也不是负数,但0是整数.
3.多属性:同一个数,可能属于多个不同的集合.如
5既是正数又是整数.
4.提醒:分数包括有限小数和无限循环小数.
归纳总结
1.具有相反意义的量应满足的条件:①意义相反;②同类的量(带有单位),数量不一定相等。
2.有理数的分类:
有理数
整数
分数
负整数
负分数
正分数
正整数
0
正有理数
负有理数
正分数
负分数
负整数
正整数
0
有理数
课堂小结
3.注意0的特殊性:0既不是正数,也不是负数.
正数和0统称为非负数.
课堂作业:习题1.1-1、2、3、4题(抄题目)
课后作业
课后作业:学法1.1
上交时间:下午上第一节课之前
晚自习第一节课前
同课章节目录
