5.2.2 递归 课件(15张PPT)
文档属性
| 名称 | 5.2.2 递归 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-10-25 18:17:18 | ||
图片预览




文档简介
(共15张PPT)
选择性必修一《数据与数据结构》
第五章 数据结构与算法
5.2.2 迭代与递归
——递归
俄罗斯套娃
分形图案生成
情境导入
返回
俄罗斯套娃
相传俄罗斯民族有两家表亲相邻,表兄妹童年相伴长大,后来表兄远走它乡,由于思念家乡的表妹,每年做木娃娃,一年比一年做的娃娃大。数年后,他回到了家乡,将娃娃送给了表妹,后人模仿传称套娃,又叫吉祥娃娃。
分形图案生成
返回
选择IDLE中的Help菜单——Turtle Demo——Fractal curves
阶乘问题
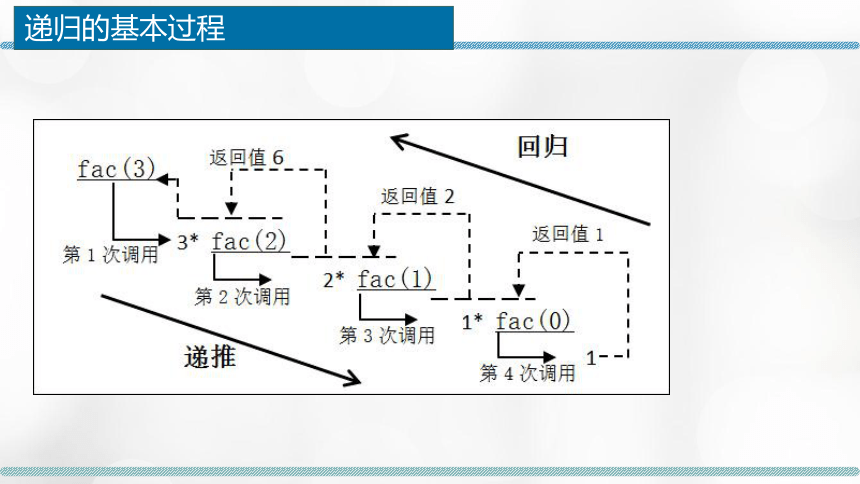
利用递归算法求n的阶乘(n!=1×2×…×n)。由数学知识可知,n阶乘的递归定义为:它等于n乘以n-1的阶乘,即n!=n*(n-1)!,并且规定0的阶乘为1。设函数fac(n)=n!,则fac(n)可表示为:
递归的基本过程
递归程序的特征
递归式:是什么
可终止:结束条件是什么
递归程序的两个条件
自主学习:递归实现斐波那契数列
递归式:
终止条件
a1 = 1
a2 = 1
an=an-1+an-2(当n>2时)
迭代算法的影响因素
终止条件的设置
初始值不同
影响迭代算法的因素
汉诺塔游戏
1. 抽象与建模
选择IDLE中的Help菜单——Turtle Demo——Minimal_Hanoi
为了将n个盘子从A柱经过B柱移动到C柱,可建立如下模型:
将n-1个盘子从A柱经过C柱移动到B柱
将A柱中剩下的一个盘子移动到C柱
将n-1个盘子从B柱经过A柱移动到C柱
汉诺塔游戏
2.设计算法
(1)定义一个实现盘子移动的函数move。如将n个盘子从A柱经过B柱移动到C柱,可调用函数move(n, a, b, c),其中,n表示A柱上的盘子个数,a、b、c分别表示A柱、B柱、C柱。
(2)将n-1个盘子从B柱经过A柱移动到C柱,可以分解成如下递归调用:
move(n-1, a, c, b)
a→c
move(n-1, b, a, c)
(3)当n=1时,直接移动盘子,递归结束。
汉诺塔游戏
3.编写程序
拓展学习:无限递归
递归算法的概念
递归算法的条件
迭代算法的实现
递归算法的数学原理与注意事项
课堂小结
学习评价
对自己和同伴的表现进行客观的评价,并思考后续完善的方向。(5=优秀,4=超出一般水平,3=满意,2=有待改进,1=不太理想)
评分项 自我评价 同学互评
能完成新课导入中的问题并总结递归算法的基本思想 5 4 3 2 1 5 4 3 2 1
掌握递归算法的一般设计思路 5 4 3 2 1 5 4 3 2 1
能够编程实现求阶乘问题 5 4 3 2 1 5 4 3 2 1
能理解递归的数学原理、注意事项 5 4 3 2 1 5 4 3 2 1
课堂作业
1.完成课本“思考与练习”第4题
2.课后练习三道题目
选择性必修一《数据与数据结构》
第五章 数据结构与算法
5.2.2 迭代与递归
——递归
俄罗斯套娃
分形图案生成
情境导入
返回
俄罗斯套娃
相传俄罗斯民族有两家表亲相邻,表兄妹童年相伴长大,后来表兄远走它乡,由于思念家乡的表妹,每年做木娃娃,一年比一年做的娃娃大。数年后,他回到了家乡,将娃娃送给了表妹,后人模仿传称套娃,又叫吉祥娃娃。
分形图案生成
返回
选择IDLE中的Help菜单——Turtle Demo——Fractal curves
阶乘问题
利用递归算法求n的阶乘(n!=1×2×…×n)。由数学知识可知,n阶乘的递归定义为:它等于n乘以n-1的阶乘,即n!=n*(n-1)!,并且规定0的阶乘为1。设函数fac(n)=n!,则fac(n)可表示为:
递归的基本过程
递归程序的特征
递归式:是什么
可终止:结束条件是什么
递归程序的两个条件
自主学习:递归实现斐波那契数列
递归式:
终止条件
a1 = 1
a2 = 1
an=an-1+an-2(当n>2时)
迭代算法的影响因素
终止条件的设置
初始值不同
影响迭代算法的因素
汉诺塔游戏
1. 抽象与建模
选择IDLE中的Help菜单——Turtle Demo——Minimal_Hanoi
为了将n个盘子从A柱经过B柱移动到C柱,可建立如下模型:
将n-1个盘子从A柱经过C柱移动到B柱
将A柱中剩下的一个盘子移动到C柱
将n-1个盘子从B柱经过A柱移动到C柱
汉诺塔游戏
2.设计算法
(1)定义一个实现盘子移动的函数move。如将n个盘子从A柱经过B柱移动到C柱,可调用函数move(n, a, b, c),其中,n表示A柱上的盘子个数,a、b、c分别表示A柱、B柱、C柱。
(2)将n-1个盘子从B柱经过A柱移动到C柱,可以分解成如下递归调用:
move(n-1, a, c, b)
a→c
move(n-1, b, a, c)
(3)当n=1时,直接移动盘子,递归结束。
汉诺塔游戏
3.编写程序
拓展学习:无限递归
递归算法的概念
递归算法的条件
迭代算法的实现
递归算法的数学原理与注意事项
课堂小结
学习评价
对自己和同伴的表现进行客观的评价,并思考后续完善的方向。(5=优秀,4=超出一般水平,3=满意,2=有待改进,1=不太理想)
评分项 自我评价 同学互评
能完成新课导入中的问题并总结递归算法的基本思想 5 4 3 2 1 5 4 3 2 1
掌握递归算法的一般设计思路 5 4 3 2 1 5 4 3 2 1
能够编程实现求阶乘问题 5 4 3 2 1 5 4 3 2 1
能理解递归的数学原理、注意事项 5 4 3 2 1 5 4 3 2 1
课堂作业
1.完成课本“思考与练习”第4题
2.课后练习三道题目
