青岛版八年级下青岛版第9章解直角三角形复习
文档属性
| 名称 | 青岛版八年级下青岛版第9章解直角三角形复习 |  | |
| 格式 | zip | ||
| 文件大小 | 816.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-01 20:37:09 | ||
图片预览


文档简介
(共17张PPT)
A
B
b
a
c
┏
C
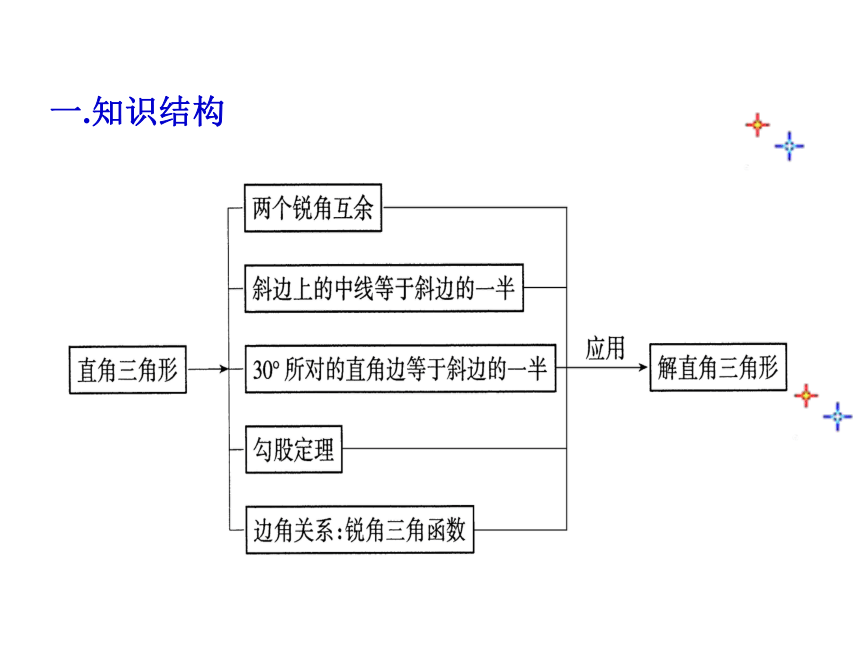
一.知识结构
二、知识要点回顾
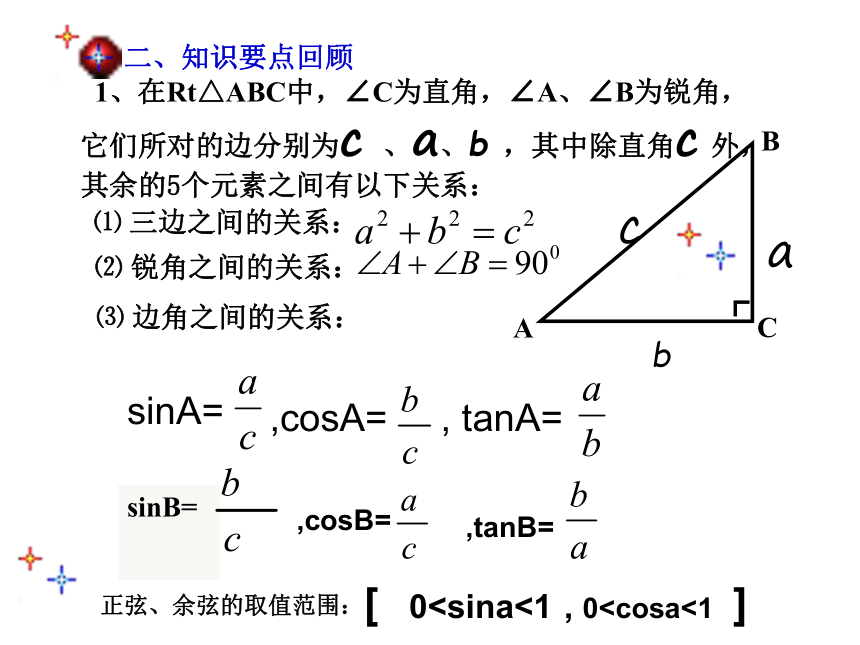
1、在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
它们所对的边分别为c 、a、b ,其中除直角c 外,
其余的5个元素之间有以下关系:
⑴ 三边之间的关系:
⑵ 锐角之间的关系:
⑶ 边角之间的关系:
A
B
b
a
c
┏
C
sinB=
[ 0sinA=
,cosA= , tanA=
,cosB=
,tanB=
正弦、余弦的取值范围:
2、
l
h
α
坡度
i=
h
l
tanα=
i
(α为坡角)
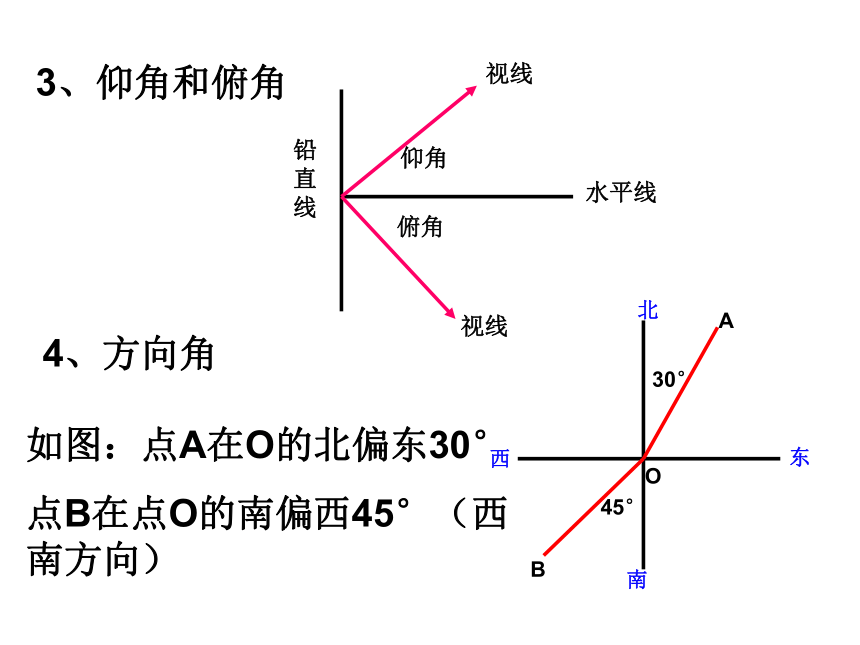
3、仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
4、方向角
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
30°
45°
B
O
A
东
西
北
南
à 300 450 600
sina
cosa
tana 1
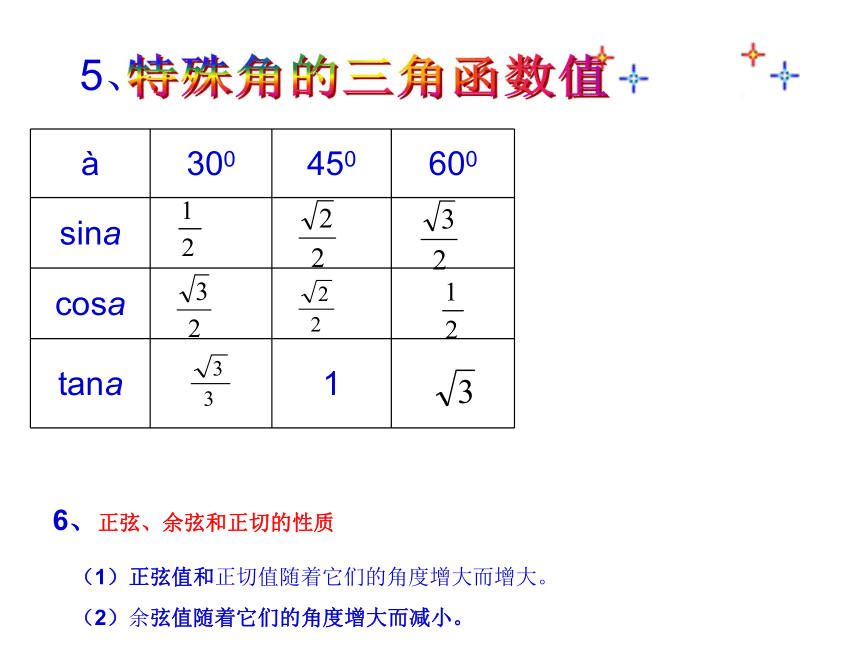
5、
6、正弦、余弦和正切的性质
(1)正弦值和正切值随着它们的角度增大而增大。
(2)余弦值随着它们的角度增大而减小。
(3)余角余函数之间的关系:
sinA=sin(90o_B)=cosB, cosA=cos(900_B)=sinB,
☆ 例题1
1.已知角,求值
求下列各式的值
2sin30°+3tan30°
=2 + d
cos245°+ tan60°cos30°
= 2
1.
2.
☆ 例题2
1.已知角,求值
求锐角A的值
2.已知值,求角
1. 已知 tanA= ,求锐角A .
已知2cosA - = 0 ,
求锐角A的度数 .
∠A=60°
∠A=30°
解:∵ 2cosA - = 0
∴ 2cosA =
∴cosA= ∴∠A= 30°
练习
1. 在△ABC中∠C=90° ,∠B=2∠A . 则cosA=______
3.已A是锐角且tanA=3,则
2. 若tan(β+20°)= ,为锐角.则β=______
在Rt△ABC中,∠C=90°,cosB= ,则sinB的值为_______.
40°
5.已知 0°<a< 45 °锐角,化简 =______
cosa-sina
例题3 在Rt△ABC中,∠C=90°:
⑴已知∠A、 c, 则a=__________;b=_________。
⑵已知∠A、 b, 则a=__________;c=_________。
⑶已知∠A、 a,则c=_________。
(4)已知a、c,则b=__________ 。
A
B
b
a
c
┏
C
⌒
对边
邻边
斜边
已知一锐角、斜边,求对边,用锐角的正弦;
求邻边,用锐角的余弦。
已知一锐角、邻边,求对边,用锐角的正切;
求斜边,用锐角的余弦。
已知一锐角、对边,求斜边,用锐角的正弦。
已知任意两边,求第三边,用勾股定理
练习、 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
A
B
C
450
300
4cm
-------------
D
提示:过A点作BC的垂直AD于D
小结
内容小结
本节课主要复习了两个部分的内容:一部分是本章的知识结构和要点;另一部分是解直角三角形及其运用其解决实际问题.
方法归纳
1.一是把直角三角形中简单基础知识通过数学模型加强理解识记,二是将已知条件转化为示意图中的边、角或它们之间的关系。
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形。同时在解的过程中可以用方程的思想解题。
中考题目精选:(08年江苏泰州)如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度i(即tan)为1︰1.2,坝高为5米。现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4。已知堤坝总长度为4000米。求完成该工程需要多少土方?
(08 山东)如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
A
B
b
a
c
┏
C
一.知识结构
二、知识要点回顾
1、在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
它们所对的边分别为c 、a、b ,其中除直角c 外,
其余的5个元素之间有以下关系:
⑴ 三边之间的关系:
⑵ 锐角之间的关系:
⑶ 边角之间的关系:
A
B
b
a
c
┏
C
sinB=
[ 0
,cosA= , tanA=
,cosB=
,tanB=
正弦、余弦的取值范围:
2、
l
h
α
坡度
i=
h
l
tanα=
i
(α为坡角)
3、仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
4、方向角
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
30°
45°
B
O
A
东
西
北
南
à 300 450 600
sina
cosa
tana 1
5、
6、正弦、余弦和正切的性质
(1)正弦值和正切值随着它们的角度增大而增大。
(2)余弦值随着它们的角度增大而减小。
(3)余角余函数之间的关系:
sinA=sin(90o_B)=cosB, cosA=cos(900_B)=sinB,
☆ 例题1
1.已知角,求值
求下列各式的值
2sin30°+3tan30°
=2 + d
cos245°+ tan60°cos30°
= 2
1.
2.
☆ 例题2
1.已知角,求值
求锐角A的值
2.已知值,求角
1. 已知 tanA= ,求锐角A .
已知2cosA - = 0 ,
求锐角A的度数 .
∠A=60°
∠A=30°
解:∵ 2cosA - = 0
∴ 2cosA =
∴cosA= ∴∠A= 30°
练习
1. 在△ABC中∠C=90° ,∠B=2∠A . 则cosA=______
3.已A是锐角且tanA=3,则
2. 若tan(β+20°)= ,为锐角.则β=______
在Rt△ABC中,∠C=90°,cosB= ,则sinB的值为_______.
40°
5.已知 0°<a< 45 °锐角,化简 =______
cosa-sina
例题3 在Rt△ABC中,∠C=90°:
⑴已知∠A、 c, 则a=__________;b=_________。
⑵已知∠A、 b, 则a=__________;c=_________。
⑶已知∠A、 a,则c=_________。
(4)已知a、c,则b=__________ 。
A
B
b
a
c
┏
C
⌒
对边
邻边
斜边
已知一锐角、斜边,求对边,用锐角的正弦;
求邻边,用锐角的余弦。
已知一锐角、邻边,求对边,用锐角的正切;
求斜边,用锐角的余弦。
已知一锐角、对边,求斜边,用锐角的正弦。
已知任意两边,求第三边,用勾股定理
练习、 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
A
B
C
450
300
4cm
-------------
D
提示:过A点作BC的垂直AD于D
小结
内容小结
本节课主要复习了两个部分的内容:一部分是本章的知识结构和要点;另一部分是解直角三角形及其运用其解决实际问题.
方法归纳
1.一是把直角三角形中简单基础知识通过数学模型加强理解识记,二是将已知条件转化为示意图中的边、角或它们之间的关系。
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形。同时在解的过程中可以用方程的思想解题。
中考题目精选:(08年江苏泰州)如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度i(即tan)为1︰1.2,坝高为5米。现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4。已知堤坝总长度为4000米。求完成该工程需要多少土方?
(08 山东)如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
