2021-2022学年人教版八年级上册数学14.2.1平方差公式 课件(共14张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级上册数学14.2.1平方差公式 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 996.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 09:33:23 | ||
图片预览





文档简介
(共14张PPT)
平方差公式
创设情境
王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
算一算:看谁做的又快又准确!
(1)
(2)
(3)
(4)
观察思考:
①等式左边相乘的两个多项式有什么特点?
②等式右边的多项式有什么规律?
③你能归纳出上述等式的规律吗?
平方差公式
证明:(a+b)(a-b)
我们经历了由发现——猜测——证明的过程,最后得出一个公式性的结论,我们将这个公式叫做平方差公式.
符号语言: (a+b)(a-b)
文字语言:两数和与这两数差的积,等于它们的平方差.
议一议
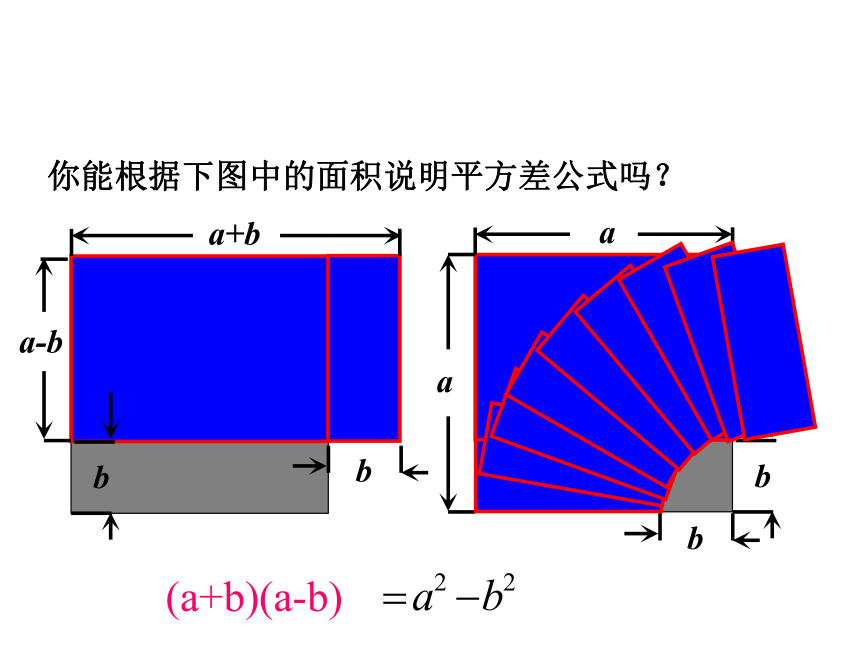
你能根据下图中的面积说明平方差公式吗?
a
a
b
b
a+b
a-b
b
b
(a+b)(a-b)
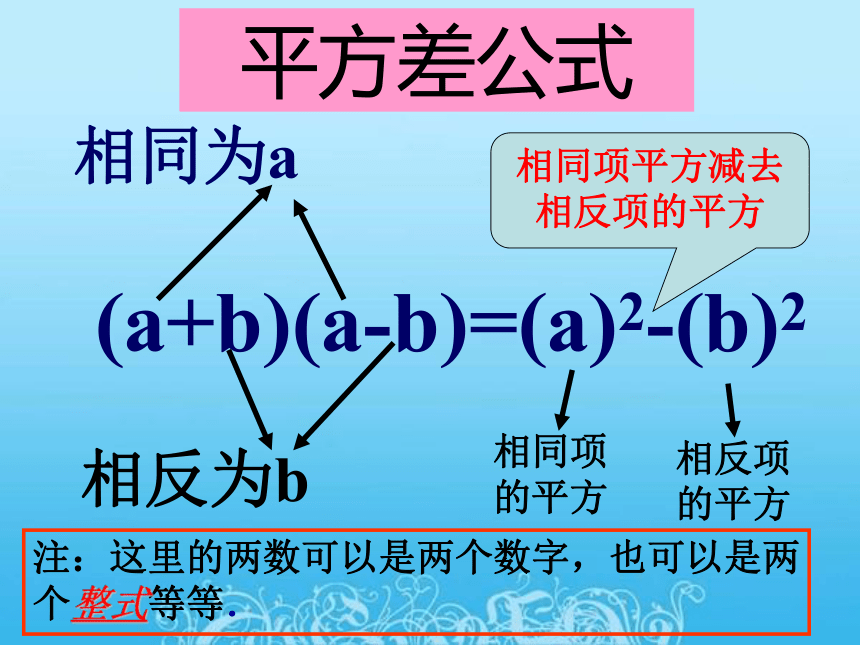
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b
相同项的平方
相反项的平方
平方差公式
注:这里的两数可以是两个数字,也可以是两个整式等等.
相同项平方减去相反项的平方
典例精析
例1 利用平方差公式计算:
(1) (5+6x )( 5-6x ) ; (2) (x-2y)(x+2y);
(3) (-m+n)(-m-n)
解:(1)原式=52-(6x)2
=25-36x2;
(2)原式=x2-(2y)2
=x2 - 4y2;
(3)原式=(-m)2-n2
=m2-n2.
(3m+2n)(3m-2n)
变式一 ( -3m+2n)(-3m-2n)
变式二 ( -3m-2n)(3m-2n)
变式三 (-3m-2n)(3m+2n)
= (-3m)2-(2n)2
变一变,你还能做吗?
= (-2n)2-(3m)2
= -(3m+2n)2
= -9m2-12mn-4n2
王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
解:李大妈吃亏了.
理由如下:原正方形的面积为a2,改变边长后面积为(a+4)(a-4)=a2-16.
∵a2>a2-16,∴李大妈吃亏了.
解决问题:
(1)(x+3)(x-3)=x2-3
(2)(-3a-1)(3a-1)=9a2-1
(3)(4x+3y)(4x-3y)=4x2-3y2
(4)(2xy-3)(2xy+3)=4xy2-9
错,x2-9
错,1-9a2
错,16x2-9y2
错,4x2y2-9
练习2 改正错误
例2 计算
(1)(x+y)(x-y)(x2+y2)
解: (x+y)(x-y)(x2+y2)
=(x2-y2)(x2+y2)
=x4-y4
(2) (x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)
= (x2-y2)(x2+y2)(x4+y4)(x8+y8)
=(x4-y4) (x4+y4)(x8+y8)
=(x8-y8 )(x8+y8)
=x16-y16
小结
试用语言表述平方差公式 (a+b)(a b)= a2 b2.
应用平方差公式时要注意一些什么?
两数和与这两数差的积,等于它们的平方差.
运用平方差公式时,要紧扣公式的特征,
找出相同的“项”和符号相反的“项”,然后应用公式.
平方差公式
课外拓展:
计算(用指数形式表示)
1、(x-1)(x+1) (x2+1)(x4+1) (x8+1) (x16+1)
2、(2+1) (22+1)(24+1) (28+1) (216+1)
3、(x+1) (x2+1)(x4+1) (x8+1) (x16+1)
作业:
计算1、10.3×9.7 2、
再见!
平方差公式
创设情境
王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
算一算:看谁做的又快又准确!
(1)
(2)
(3)
(4)
观察思考:
①等式左边相乘的两个多项式有什么特点?
②等式右边的多项式有什么规律?
③你能归纳出上述等式的规律吗?
平方差公式
证明:(a+b)(a-b)
我们经历了由发现——猜测——证明的过程,最后得出一个公式性的结论,我们将这个公式叫做平方差公式.
符号语言: (a+b)(a-b)
文字语言:两数和与这两数差的积,等于它们的平方差.
议一议
你能根据下图中的面积说明平方差公式吗?
a
a
b
b
a+b
a-b
b
b
(a+b)(a-b)
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b
相同项的平方
相反项的平方
平方差公式
注:这里的两数可以是两个数字,也可以是两个整式等等.
相同项平方减去相反项的平方
典例精析
例1 利用平方差公式计算:
(1) (5+6x )( 5-6x ) ; (2) (x-2y)(x+2y);
(3) (-m+n)(-m-n)
解:(1)原式=52-(6x)2
=25-36x2;
(2)原式=x2-(2y)2
=x2 - 4y2;
(3)原式=(-m)2-n2
=m2-n2.
(3m+2n)(3m-2n)
变式一 ( -3m+2n)(-3m-2n)
变式二 ( -3m-2n)(3m-2n)
变式三 (-3m-2n)(3m+2n)
= (-3m)2-(2n)2
变一变,你还能做吗?
= (-2n)2-(3m)2
= -(3m+2n)2
= -9m2-12mn-4n2
王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
解:李大妈吃亏了.
理由如下:原正方形的面积为a2,改变边长后面积为(a+4)(a-4)=a2-16.
∵a2>a2-16,∴李大妈吃亏了.
解决问题:
(1)(x+3)(x-3)=x2-3
(2)(-3a-1)(3a-1)=9a2-1
(3)(4x+3y)(4x-3y)=4x2-3y2
(4)(2xy-3)(2xy+3)=4xy2-9
错,x2-9
错,1-9a2
错,16x2-9y2
错,4x2y2-9
练习2 改正错误
例2 计算
(1)(x+y)(x-y)(x2+y2)
解: (x+y)(x-y)(x2+y2)
=(x2-y2)(x2+y2)
=x4-y4
(2) (x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)
= (x2-y2)(x2+y2)(x4+y4)(x8+y8)
=(x4-y4) (x4+y4)(x8+y8)
=(x8-y8 )(x8+y8)
=x16-y16
小结
试用语言表述平方差公式 (a+b)(a b)= a2 b2.
应用平方差公式时要注意一些什么?
两数和与这两数差的积,等于它们的平方差.
运用平方差公式时,要紧扣公式的特征,
找出相同的“项”和符号相反的“项”,然后应用公式.
平方差公式
课外拓展:
计算(用指数形式表示)
1、(x-1)(x+1) (x2+1)(x4+1) (x8+1) (x16+1)
2、(2+1) (22+1)(24+1) (28+1) (216+1)
3、(x+1) (x2+1)(x4+1) (x8+1) (x16+1)
作业:
计算1、10.3×9.7 2、
再见!
