2021-2022学年人教版七年级数学上 册1.2.3 相反数课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上 册1.2.3 相反数课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 567.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
相反数
整数和分数统称有理数。
整数包括正整数、零和负整数。
不能忘了零。
分数包括正分数和负分数。
有限小数、无限循环小数、百分数也是分数。
知识回顾
数轴三要素:原点、单位长度和正方向。原点右边的数表示正数 ,原点左边的数表示负数。
拿任何一个数字对着我照一下,就可以得到符号不同的另外一个数字。
像-1和1,-0.5和0.5这样只有符号不同的两个数,我们称这两个数互为相反数,其中一个数为另一个数的相反数。
神
奇
的
镜
子
我出道题给你们,估计没人做的出来吧!毕竟我是神奇的镜子!
-7、 、-20%的相反数分别是多少?
7、 - 、20%
没想到你们都能做出来,真厉害!
a的相反数是-a。即求一个数的相反数就是在前面添个负号。
如:-a表示的是a的相反数。
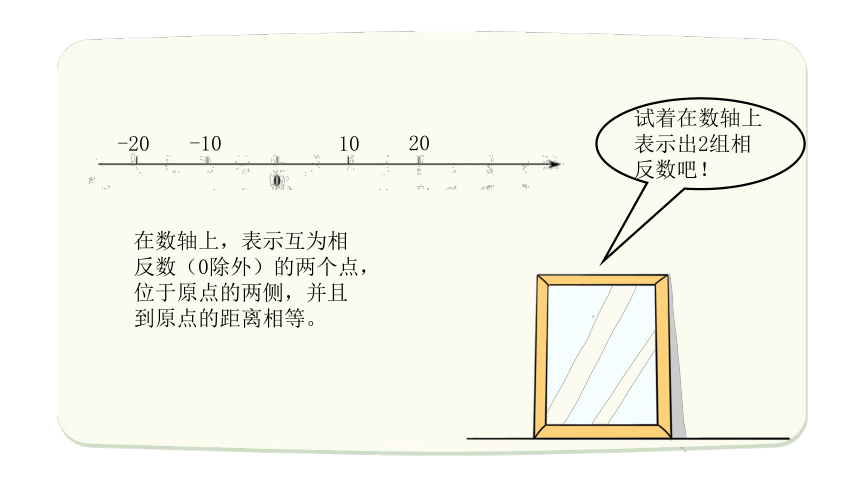
试着在数轴上表示出2组相反数吧!
在数轴上,表示互为相反数(0除外)的两个点,位于原点的两侧,并且到原点的距离相等。
10
-10
20
-20
已知3m-2与-7互为相反数,求m的值.
-7的相反数是多少呢?
解析思路:-7的相反数是7
3m-2=7
解出m的值即可
解答过程:
解:∵3m-2与-7互为相反数,
∴3m-2=7,
解得m=3.
也就是说3m-2等于.......
利用相反数的性质解题的一般思路:
(1)理解相反数的定义:若 a 与 b 互为相反数,则 a = -b ;
(2)根据等量关系,列方程求解。
计算:-[ -(+43)]= ____
①先去小括号,-(+43)
表示+43的相反数是-43
②化简为-(-43),这个
表示-43的相反数是43
解答过程:
解:-[-(+43)]=(+43)=43.
故答案为:43.
43
题型对比1
下面2道题有什么规律呢?我们一起分析下吧!
计算:-[-(-3.6)]= ____
①先去小括号,-(-3.6)表示
-3.6的相反数是3.6
②化简为-(3.6),这个表示
3.6的相反数是-3.6
解答过程:
解:-[-(-3.6)]=-(+3.6)=-3.6
故答案为:-3.6.
-3.6
下面2道题有什么规律呢?我们一起分析下吧!
题型对比2
计算:-[ -(+43)]= ____
计算:-[-(-3.6)]= ____
分析
43前面有两个负号,最后得出的结果是个正数
3.6前面有三个负号,最后得出的结果是个负数
43
-3.6
一个正数前面有偶数个“-”, 结果为正;一个数前面有奇数个“-”, 结果为负。
注意:0 前面无论有几个符号,结果都为 0.
你发现了吗?
相反数多重符号的化简问题的一般思路:
把所有的“+”号去掉,由“-”号的个数决定:
①一个数前面有偶数个“-”, 结果为正;
②一个数前面有奇数个“-”, 结果为负。
已知数轴上点A表示的数为5,点B、C表示互为相反数的两个数,且点C与点A间的距离为2.求点B、C表示的数.
先画个数轴,找到A的位置吧!
C位置怎么确定?
A
C2
C1
-3
-7
已知数轴上点A表示的数为5,点B、C表示互为相反数的两个数,且点C与点A间的距离为2.求点B、C表示的数.
我们一起整理下解题思路
吧!
解析思路:在数轴找出距离A点两个单
位长度的点为3和7,分别用
C1、C2表示,要进行分类讨论;
当B与C2互为相反数时,B表示的
数是-7;
当B与C1互为相反数时,B表示
的数是-3;
A
C2
C1
-3
-7
已知数轴上点A表示的数为5,点B、C表示互为相反数的两个数,且点C与点A间的距离为2.求点B、C表示的数.
A
C2
C1
B
B
解:∵数轴上点A表示的数为5,且点C与点A间的距离为2
∴点C表示的数为3或7
∵点B、C表示互为相反数的两个数
∴点B表示的数为-3或-7.
∴点B表示的数为-3或-7,点C表示的数为3或7.
我们一起总结下吧!
相反数解决问题的一般思路:
(1)画出数轴,在数轴上标出已知点的位置;
(2)求出与已知点距离一定单位长度的点表示的数;
(3)根据相反数的概念,求出另一个点表示的数。
(1)有理数是整数与分数的统称;
(2)b的相反数是-b。0的相反数是0。
(3)一个数字前面有偶数个“-”, 结果为正;一个数
字前面有奇数个“-”, 结果为负。
相反数
整数和分数统称有理数。
整数包括正整数、零和负整数。
不能忘了零。
分数包括正分数和负分数。
有限小数、无限循环小数、百分数也是分数。
知识回顾
数轴三要素:原点、单位长度和正方向。原点右边的数表示正数 ,原点左边的数表示负数。
拿任何一个数字对着我照一下,就可以得到符号不同的另外一个数字。
像-1和1,-0.5和0.5这样只有符号不同的两个数,我们称这两个数互为相反数,其中一个数为另一个数的相反数。
神
奇
的
镜
子
我出道题给你们,估计没人做的出来吧!毕竟我是神奇的镜子!
-7、 、-20%的相反数分别是多少?
7、 - 、20%
没想到你们都能做出来,真厉害!
a的相反数是-a。即求一个数的相反数就是在前面添个负号。
如:-a表示的是a的相反数。
试着在数轴上表示出2组相反数吧!
在数轴上,表示互为相反数(0除外)的两个点,位于原点的两侧,并且到原点的距离相等。
10
-10
20
-20
已知3m-2与-7互为相反数,求m的值.
-7的相反数是多少呢?
解析思路:-7的相反数是7
3m-2=7
解出m的值即可
解答过程:
解:∵3m-2与-7互为相反数,
∴3m-2=7,
解得m=3.
也就是说3m-2等于.......
利用相反数的性质解题的一般思路:
(1)理解相反数的定义:若 a 与 b 互为相反数,则 a = -b ;
(2)根据等量关系,列方程求解。
计算:-[ -(+43)]= ____
①先去小括号,-(+43)
表示+43的相反数是-43
②化简为-(-43),这个
表示-43的相反数是43
解答过程:
解:-[-(+43)]=(+43)=43.
故答案为:43.
43
题型对比1
下面2道题有什么规律呢?我们一起分析下吧!
计算:-[-(-3.6)]= ____
①先去小括号,-(-3.6)表示
-3.6的相反数是3.6
②化简为-(3.6),这个表示
3.6的相反数是-3.6
解答过程:
解:-[-(-3.6)]=-(+3.6)=-3.6
故答案为:-3.6.
-3.6
下面2道题有什么规律呢?我们一起分析下吧!
题型对比2
计算:-[ -(+43)]= ____
计算:-[-(-3.6)]= ____
分析
43前面有两个负号,最后得出的结果是个正数
3.6前面有三个负号,最后得出的结果是个负数
43
-3.6
一个正数前面有偶数个“-”, 结果为正;一个数前面有奇数个“-”, 结果为负。
注意:0 前面无论有几个符号,结果都为 0.
你发现了吗?
相反数多重符号的化简问题的一般思路:
把所有的“+”号去掉,由“-”号的个数决定:
①一个数前面有偶数个“-”, 结果为正;
②一个数前面有奇数个“-”, 结果为负。
已知数轴上点A表示的数为5,点B、C表示互为相反数的两个数,且点C与点A间的距离为2.求点B、C表示的数.
先画个数轴,找到A的位置吧!
C位置怎么确定?
A
C2
C1
-3
-7
已知数轴上点A表示的数为5,点B、C表示互为相反数的两个数,且点C与点A间的距离为2.求点B、C表示的数.
我们一起整理下解题思路
吧!
解析思路:在数轴找出距离A点两个单
位长度的点为3和7,分别用
C1、C2表示,要进行分类讨论;
当B与C2互为相反数时,B表示的
数是-7;
当B与C1互为相反数时,B表示
的数是-3;
A
C2
C1
-3
-7
已知数轴上点A表示的数为5,点B、C表示互为相反数的两个数,且点C与点A间的距离为2.求点B、C表示的数.
A
C2
C1
B
B
解:∵数轴上点A表示的数为5,且点C与点A间的距离为2
∴点C表示的数为3或7
∵点B、C表示互为相反数的两个数
∴点B表示的数为-3或-7.
∴点B表示的数为-3或-7,点C表示的数为3或7.
我们一起总结下吧!
相反数解决问题的一般思路:
(1)画出数轴,在数轴上标出已知点的位置;
(2)求出与已知点距离一定单位长度的点表示的数;
(3)根据相反数的概念,求出另一个点表示的数。
(1)有理数是整数与分数的统称;
(2)b的相反数是-b。0的相反数是0。
(3)一个数字前面有偶数个“-”, 结果为正;一个数
字前面有奇数个“-”, 结果为负。
