2021—2022学年湘教版数学八年级上册2.3 等腰三角形课件(18张)
文档属性
| 名称 | 2021—2022学年湘教版数学八年级上册2.3 等腰三角形课件(18张) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 10:54:00 | ||
图片预览



文档简介
(共18张PPT)
猜一猜
形状像座山,稳定性能强.
三竿首尾连,两竿一样长.
(打一数学图形-- )
等腰三角形
等腰三角形的
性质
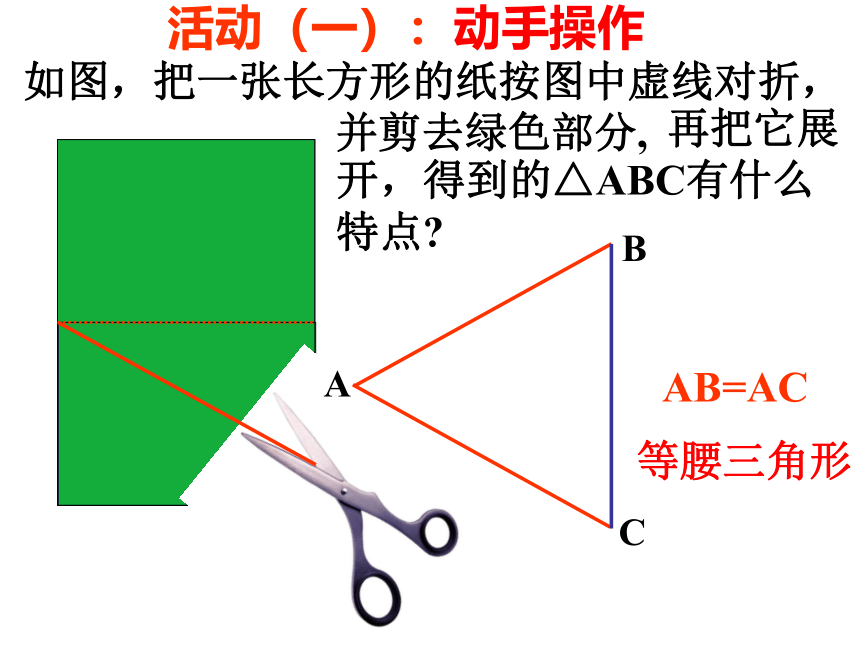
知识回顾:
A
B
C
等腰三角形:
有两条边相等的三角形.
相等的两条边叫作腰,
另一条边叫作底边,
底边与腰的夹角叫作底角.
两腰所夹的角叫作顶角,
腰
腰
底边
顶角
底角
如图,把一张长方形的纸按图中虚线对折,
并剪去绿色部分,
再把它展开,得到的△ABC有什么特点
A
B
C
AB=AC
等腰三角形
活动(一):动手操作
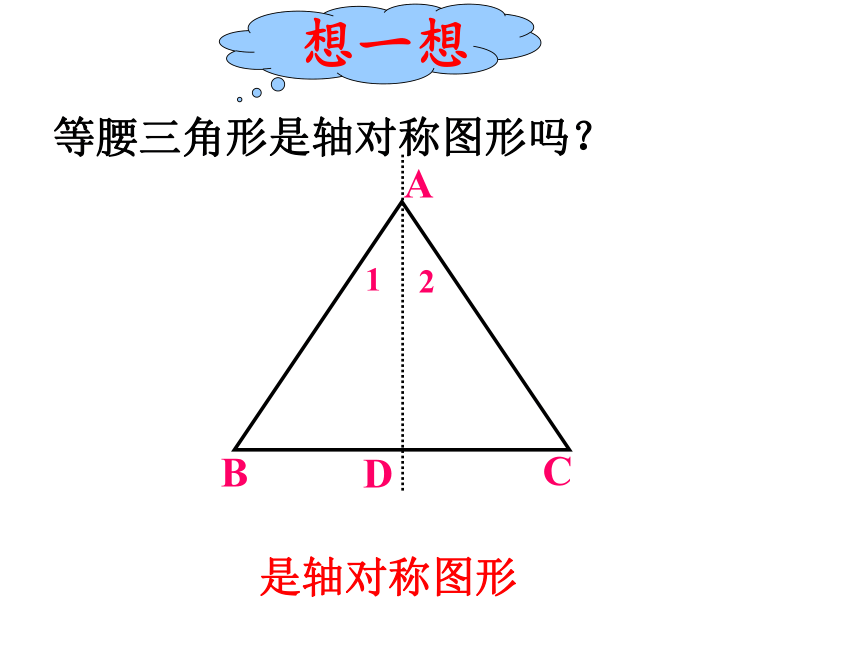
等腰三角形是轴对称图形吗?
是轴对称图形
想一想
A
B
C
D
2
1
A
B
C
D
2
1
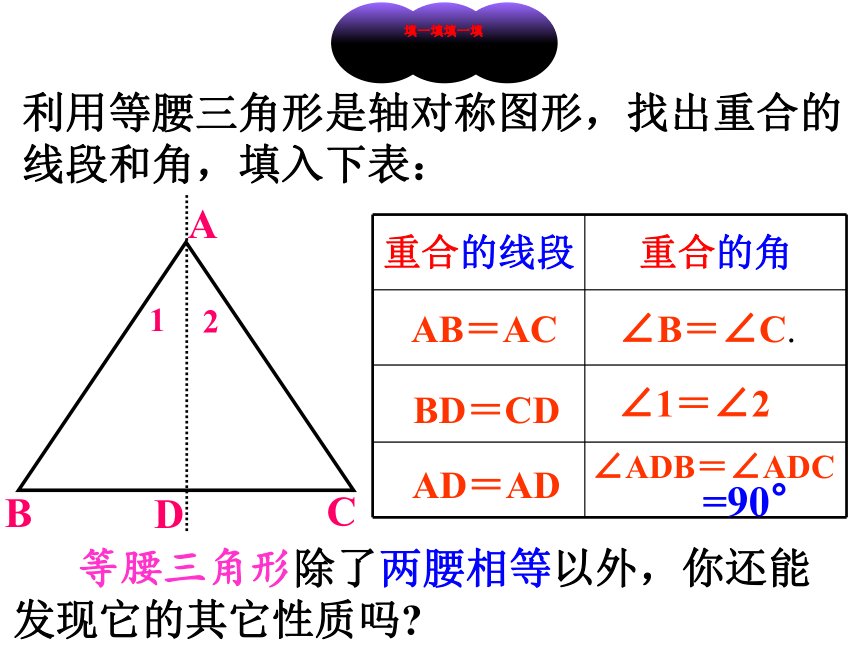
重合的线段 重合的角
AB=AC
BD=CD
AD=AD
∠B=∠C.
∠1=∠2
∠ADB=∠ADC
填一填
=90°
利用等腰三角形是轴对称图形,找出重合的线段和角,填入下表:
等腰三角形除了两腰相等以外,你还能发现它的其它性质吗
在△ABC中, ∵ AB= AC,
等腰三角形两底角的大小有什么关系?
C
A
B
探究一
等腰三角形的两个底角______.
B
(简写成“等边对等角”).
性质1:
几何语言:
相等
∴∠C =∠___.
∠1=∠2
AD是△ABC顶角
的__________.
BD=CD
AD是△ABC底边
BC上的______.
∠ADB=∠ADC
AD是△ABC底边
BC上的___.
角平分线
中线
高
A
B
D
C
┐
探究二
思考:等腰三角形底边上的高、中线及
顶角平分线有什么关系?
1
2
△ABC中,AB=AC.
A
B
D
C
(3) ∵ AD是顶角平分线,
∴ AD⊥____ ,BD =_____.
(1) ∵AD⊥BC,
∴∠BAD = ∠_____,BD= ____.
在△ABC 中, AB=AC
(2) ∵ AD是BC边的中线,
∴ AD⊥____ ,∠BAD =∠_____.
CAD
CAD
BC
BC
CD
CD
性质2:等腰三角形底边上的高、中线及
顶角平分线_____.
(“三线合一”)
几何语言:
重合
知一得二
等腰三角形的性质
3.等腰三角形底边上的高、中线及顶角平分线
重合(简称“___________”)
1.等腰三角形是轴对称图形,
对称轴是____________所在的直线.
2.等腰三角形的两底角相等(简称“___________”)
三线合一
等边对等角
顶角平分线
底边上的高
底边上的中线
如图,AB∥CD,点E在BC上,且CD=CE,∠D=74°,则∠B的度数为( )
A.68°
B.32°
C.22°
D.16°
练一练
B
如图,在△ABC中,AB=AC,AD⊥BC于
点D.若AB=6,CD=4,则△ABC的周长是 .
练一练
┐
20
如图,在已知△ABC中,AB=AC,BD=DC,则下列结论中:
①∠1=∠2; ②∠BAC=∠B;
③AD⊥BC; ④∠B=∠C.
正确的有( )
A.1个
B.2个
C.3个
D.4个
练一练
C
3.等腰三角形底边上的高、中线及顶角平分线
重合(简称“___________”)
1.等腰三角形是轴对称图形,
对称轴是____________所在的直线.
2.等腰三角形的两底角相等(简称“___________”)
三线合一
等边对等角
顶角平分线
说说这节课你有什么收获?
课堂小结
底边上的高
底边上的中线
如图,点D、E在△ABC的BC边上,AB=AC,AD=AE.求证:BD=CE.
F
证明:过点A作AF⊥BC于点F.
想 一 想
例 题
已知:如图,在△ABC中,AB=AC,点D,
E在边BC上,且AD=AE.
求证:BD=CE.
证明:过点A作AF⊥BC,垂足为点F,
∴ BF = CF
∴BF-DF=CF-EF,
即 BD=CE.
在△ABC中, ∵ AB=AC , AF⊥BC
∴ DF = EF
在△ABC中, ∵ AD=AE , AF⊥DE
动脑筋
等边三角形
1、等边三角形三条边相等,
即:AB=AC=BC
2、等边三角形是轴对称图形,
它有三条对称轴
60 °
60 °
60 °
即:∠A=∠B=∠C=60°
三个角都相等,且等于60°
有什么特殊的性质?
课堂大比武:
4. 如图,在△ABC中,AB=AC,AD为BC边上的高, ∠BAC=50°,BC= 4,求∠BAD的度数及DC的长.
解: ∵在△ABC中,AB=AC AD ⊥ BC
∴ ∠ BAD=∠CAD= ∠BAC=25°
CD=BD= BC=2
1
2
1
2
⒈ 等腰三角形一个底角为75°,
它的另外两个角为__________
⒉ 等腰三角形一个角为70°,
它的另外两个角为__________
⒊ 等腰三角形一个角为110°,
它的另外两个角为__________
75° , 30°
70° , 40°或55° , 55°
35° , 35°
猜一猜
形状像座山,稳定性能强.
三竿首尾连,两竿一样长.
(打一数学图形-- )
等腰三角形
等腰三角形的
性质
知识回顾:
A
B
C
等腰三角形:
有两条边相等的三角形.
相等的两条边叫作腰,
另一条边叫作底边,
底边与腰的夹角叫作底角.
两腰所夹的角叫作顶角,
腰
腰
底边
顶角
底角
如图,把一张长方形的纸按图中虚线对折,
并剪去绿色部分,
再把它展开,得到的△ABC有什么特点
A
B
C
AB=AC
等腰三角形
活动(一):动手操作
等腰三角形是轴对称图形吗?
是轴对称图形
想一想
A
B
C
D
2
1
A
B
C
D
2
1
重合的线段 重合的角
AB=AC
BD=CD
AD=AD
∠B=∠C.
∠1=∠2
∠ADB=∠ADC
填一填
=90°
利用等腰三角形是轴对称图形,找出重合的线段和角,填入下表:
等腰三角形除了两腰相等以外,你还能发现它的其它性质吗
在△ABC中, ∵ AB= AC,
等腰三角形两底角的大小有什么关系?
C
A
B
探究一
等腰三角形的两个底角______.
B
(简写成“等边对等角”).
性质1:
几何语言:
相等
∴∠C =∠___.
∠1=∠2
AD是△ABC顶角
的__________.
BD=CD
AD是△ABC底边
BC上的______.
∠ADB=∠ADC
AD是△ABC底边
BC上的___.
角平分线
中线
高
A
B
D
C
┐
探究二
思考:等腰三角形底边上的高、中线及
顶角平分线有什么关系?
1
2
△ABC中,AB=AC.
A
B
D
C
(3) ∵ AD是顶角平分线,
∴ AD⊥____ ,BD =_____.
(1) ∵AD⊥BC,
∴∠BAD = ∠_____,BD= ____.
在△ABC 中, AB=AC
(2) ∵ AD是BC边的中线,
∴ AD⊥____ ,∠BAD =∠_____.
CAD
CAD
BC
BC
CD
CD
性质2:等腰三角形底边上的高、中线及
顶角平分线_____.
(“三线合一”)
几何语言:
重合
知一得二
等腰三角形的性质
3.等腰三角形底边上的高、中线及顶角平分线
重合(简称“___________”)
1.等腰三角形是轴对称图形,
对称轴是____________所在的直线.
2.等腰三角形的两底角相等(简称“___________”)
三线合一
等边对等角
顶角平分线
底边上的高
底边上的中线
如图,AB∥CD,点E在BC上,且CD=CE,∠D=74°,则∠B的度数为( )
A.68°
B.32°
C.22°
D.16°
练一练
B
如图,在△ABC中,AB=AC,AD⊥BC于
点D.若AB=6,CD=4,则△ABC的周长是 .
练一练
┐
20
如图,在已知△ABC中,AB=AC,BD=DC,则下列结论中:
①∠1=∠2; ②∠BAC=∠B;
③AD⊥BC; ④∠B=∠C.
正确的有( )
A.1个
B.2个
C.3个
D.4个
练一练
C
3.等腰三角形底边上的高、中线及顶角平分线
重合(简称“___________”)
1.等腰三角形是轴对称图形,
对称轴是____________所在的直线.
2.等腰三角形的两底角相等(简称“___________”)
三线合一
等边对等角
顶角平分线
说说这节课你有什么收获?
课堂小结
底边上的高
底边上的中线
如图,点D、E在△ABC的BC边上,AB=AC,AD=AE.求证:BD=CE.
F
证明:过点A作AF⊥BC于点F.
想 一 想
例 题
已知:如图,在△ABC中,AB=AC,点D,
E在边BC上,且AD=AE.
求证:BD=CE.
证明:过点A作AF⊥BC,垂足为点F,
∴ BF = CF
∴BF-DF=CF-EF,
即 BD=CE.
在△ABC中, ∵ AB=AC , AF⊥BC
∴ DF = EF
在△ABC中, ∵ AD=AE , AF⊥DE
动脑筋
等边三角形
1、等边三角形三条边相等,
即:AB=AC=BC
2、等边三角形是轴对称图形,
它有三条对称轴
60 °
60 °
60 °
即:∠A=∠B=∠C=60°
三个角都相等,且等于60°
有什么特殊的性质?
课堂大比武:
4. 如图,在△ABC中,AB=AC,AD为BC边上的高, ∠BAC=50°,BC= 4,求∠BAD的度数及DC的长.
解: ∵在△ABC中,AB=AC AD ⊥ BC
∴ ∠ BAD=∠CAD= ∠BAC=25°
CD=BD= BC=2
1
2
1
2
⒈ 等腰三角形一个底角为75°,
它的另外两个角为__________
⒉ 等腰三角形一个角为70°,
它的另外两个角为__________
⒊ 等腰三角形一个角为110°,
它的另外两个角为__________
75° , 30°
70° , 40°或55° , 55°
35° , 35°
同课章节目录
