第25章图形的相似 同步达标测评 2021-2022学年 冀教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 第25章图形的相似 同步达标测评 2021-2022学年 冀教版九年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 382.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 11:00:14 | ||
图片预览



文档简介
2021-2022学年冀教版九年级数学上册《第25章图形的相似》同步达标测评(附答案)
一.选择题(共10小题,满分50分)
1.已知线段a=4,b=16,线段c是a、b的比例中项,那么c等于( )
A.10 B.8 C.﹣8 D.±8
2.如果x:y=2:3,则下列各式不成立的是( )
A. B. C. D.
3.已知线段a、b,求作线段x,使,正确的作法是( )
A. B.
C. D.
4.考虑下面4个命题:①有一个角是100°的两个等腰三角形相似;②斜边和周长对应相等的两个直角三角形全等;③对角线互相垂直且相等的四边形是正方形;④对角线相等的梯形是等腰梯形.其中正确命题的序号是( )
A.①②③④ B.①③④ C.①②④ D.②③④
5.如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )
A.4对 B.5对 C.6对 D.7对
6.如图,在△ABC中,EF∥BC,=,S四边形BCFE=8,则S△ABC=( )
A.9 B.10 C.12 D.13
7.宽与长的比是(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连接EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
A.矩形ABFE B.矩形EFCD C.矩形EFGH D.矩形DCGH
8.如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点P使△PAD和△PBC相似,则这样的点P存在的个数有( )
A.1 B.2 C.3 D.4
9.如图,已知△ABC三个顶点的坐标分别为(1,2),(﹣2,3),(﹣1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点A′,B′,C′.下列说法正确的是( )
A.△A′B′C′与△ABC是位似图形,位似中心是点(1,0)
B.△A′B′C′与△ABC是位似图形,位似中心是点(0,0)
C.△A′B′C′与△ABC是相似图形,但不是位似图形
D.△A′B′C′与△ABC不是相似图形
10.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2020个正方形的面积为( )
A. B. C.5×()2020 D.5×()4038
二.填空题(共6小题,满分30分)
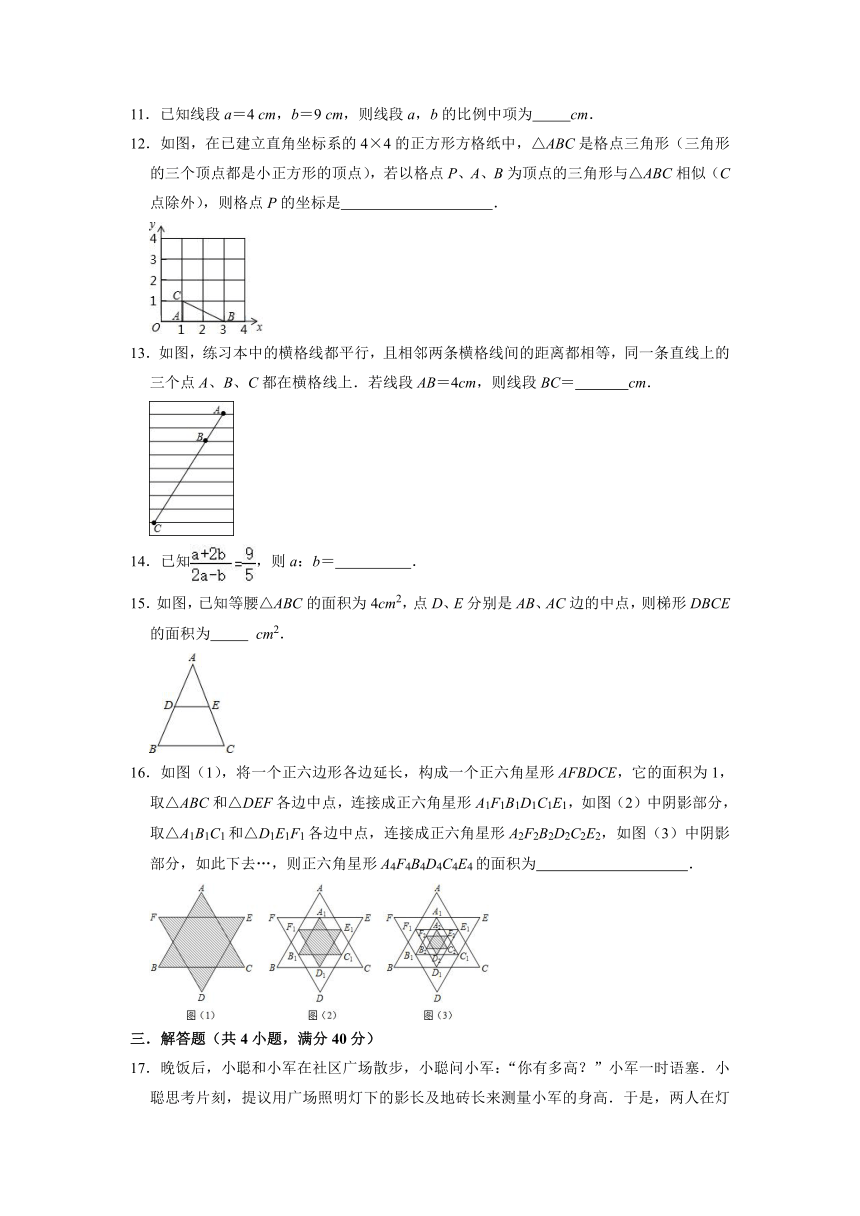
11.已知线段a=4 cm,b=9 cm,则线段a,b的比例中项为 cm.
12.如图,在已建立直角坐标系的4×4的正方形方格纸中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P、A、B为顶点的三角形与△ABC相似(C点除外),则格点P的坐标是 .
13.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC= cm.
14.已知,则a:b= .
15.如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为 cm2.
16.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分,取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分,如此下去…,则正六角星形A4F4B4D4C4E4的面积为 .
三.解答题(共4小题,满分40分)
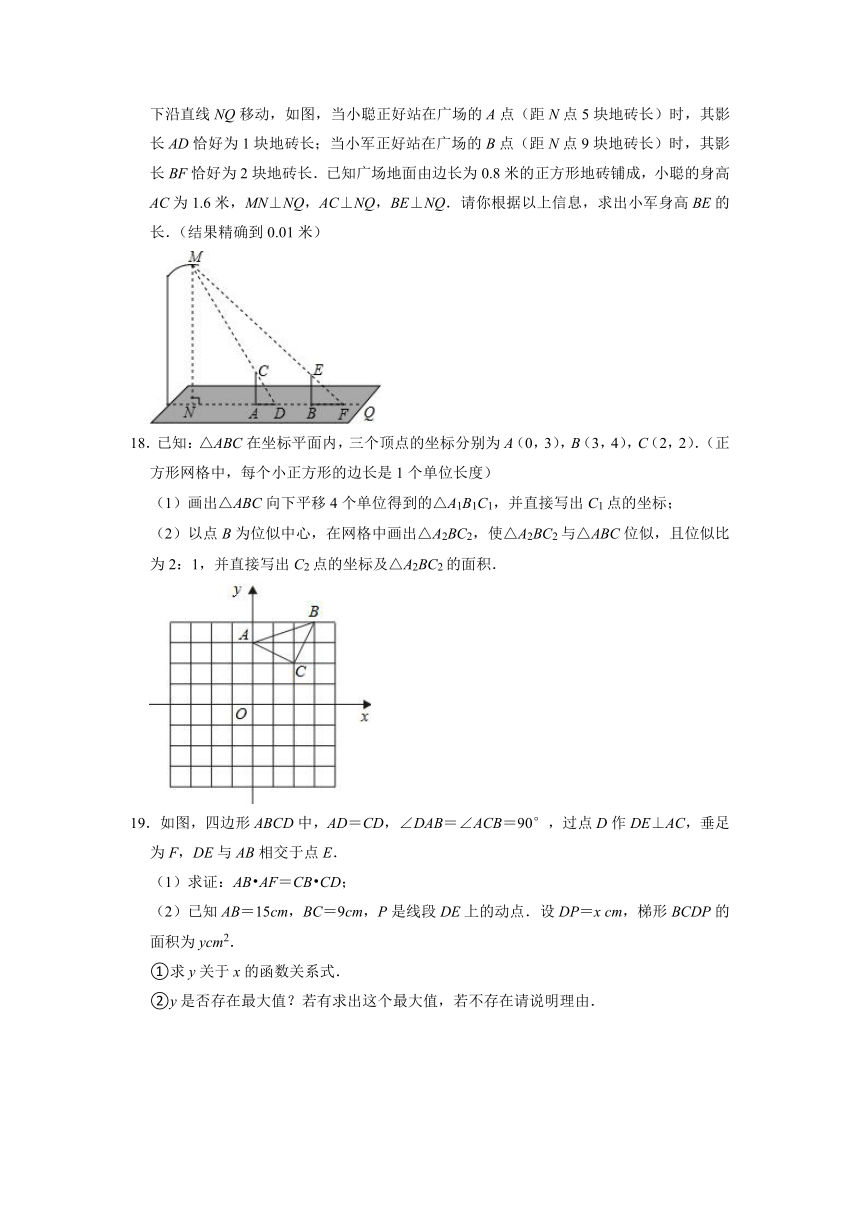
17.晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长.(结果精确到0.01米)
18.已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2:1,并直接写出C2点的坐标及△A2BC2的面积.
19.如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.
(1)求证:AB AF=CB CD;
(2)已知AB=15cm,BC=9cm,P是线段DE上的动点.设DP=x cm,梯形BCDP的面积为ycm2.
①求y关于x的函数关系式.
②y是否存在最大值?若有求出这个最大值,若不存在请说明理由.
20.如图,在矩形ABCD中,AD=4cm,AB=m(m>4),点P是AB边上的任意一点(不与点A、B重合),连接PD,过点P作PQ⊥PD,交直线BC于点Q.
(1)当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由;
(2)连接AC,若PQ∥AC,求线段BQ的长(用含m的代数式表示);
(3)若△PQD为等腰三角形,求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式,并写出m的取值范围.
参考答案
一.选择题(共10小题,满分50分)
1.解:∵线段c是a、b的比例中项,
∴c2=ab=64,
解得c=±8,
又∵线段是正数,
∴c=8.
故选:B.
2.解:可设x=2k,y=3k.通过代入计算,
进行约分,A,B,C都正确;
D不能实现约分,故错误.
故选:D.
3.解:由题意,
∴,
∵线段x没法先作出,
∴B选项错误,
根据平行线分线段成比例定理,只有C符合.
故选:C.
4.解:①正确,因为已知一个角为100°和等腰三角形,没有指出该角是顶角还是底角,根据三角形内角和公式得,该角为顶角,又因为是等腰三角形则两腰对应成比例,所以这两个等腰三角形相似;
②正确,因为两个直角三角形的斜边相等,周长对应相等,由于均为直角三角形且周长相等,两直角边长的和及平方和均为定值,知道a+b及a平方+b平方,ab亦确定,而已知a+b,ab均为正的定值,就本题而言,a,b值具有对称性(如一三角形两直角边为3,4则另一三角形两直角边必定也为一个3,一个4),最终两三角形边均对应相等,必定全等;
③错误,因为对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,既是矩形又是菱形的四边形是正方形,所以,对角线互相垂直且相等的平行四边形是正方形;
④正确,可以根据等腰梯形的判定得到.
故选:C.
5.解:图中相似三角形有△ABC∽△CDA,△AGE∽△ABC,△AFE∽△CBE,△BGE∽△BAF,△AGE∽△CDA共5对,
理由是:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,AB=CD,∠D=∠ABC,
∴△ABC≌△CDA,即△ABC∽△CDA,
∵GE∥BC,
∴△AGE∽△ABC∽△CDA,
∵GE∥BC,AD∥BC,
∴GE∥AD,
∴△BGE∽△BAF,
∵AD∥BC,
∴△AFE∽△CBE.
故选:B.
6.解:∵=,
∴==,
∵EF∥BC,
∴△AEF∽△ABC,
∴==,
∴9S△AEF=S△ABC,
∵S四边形BCFE=8,
∴9(S△ABC﹣8)=S△ABC,
解得:S△ABC=9.
故选:A.
7.解:设正方形的边长为2,则CD=2,CF=1
在直角三角形DCF中,DF==
∴FG=
∴CG=﹣1
∴=
∴矩形DCGH为黄金矩形
故选:D.
8.解:∵AD∥BC,∠D=90°
∴∠C=∠D=90°
∵DC=7,AD=2,BC=4
设PD=x,则PC=7﹣x;
①若PD:PC=AD:BC,则△PAD∽△PBC
∴,解得:PD=
②若PD:BC=AD:PC,则△PAD∽△BPC
∴,解得:PD=,
∴这样的点P存在的个数有3个.
故选:C.
9.解:∵△ABC三个顶点的坐标分别为(1,2),(﹣2,3),(﹣1,0),把它们的横坐标和纵坐标都扩大到原来的2倍
∴点A′,B′,C′的坐标分别为(2,4),(﹣4,6),(﹣2,0)
∴直线AA′,BB′,CC′得解析式分别为y=2x,y=﹣x,y=0
∴对应点的连线交于原点
∴△A′B′C′与△ABC是位似图形,位似中心是点(0,0)
故选:B.
10.
解:设正方形的面积分别为S1,S2…S2010,
根据题意,得:AD∥BC∥C1A2∥C2B2,
∴∠BAA1=∠B1A1A2=∠B2A2x(同位角相等).
∵∠ABA1=∠A1B1A2=90°,
∴△BAA1∽△B1A1A2,
在直角△ADO中,根据勾股定理,得:AD=,
∴BA1=AB=,
∴CA1=+=×,
同理,得:C1A2=××,
由正方形的面积公式,得:S1=,
S2=×,S3=××,
由此,可得Sn=×(1+)2n﹣2,
∴S2020=5×()2×2020﹣2,
=5×()4038.
故选:D.
二.填空题(共6小题,满分30分)
11.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
设它们的比例中项是x,则x2=4×9,x=±6,(线段是正数,负值舍去),故填6.
12.解:如图:此时AB对应P1A或P2B,且相似比为1:2,
故点P的坐标为:(1,4)或(3,4);
△ABC≌△BAP3,
此时P的坐标为(3,1);
∴格点P的坐标是(1,4)或(3,1)或(3,4).
13.解:如图,过点A作AE⊥CE于点E,交BD于点D,
∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,
∴,
即,
∴BC=12cm.
故答案为:12.
14.解:∵
∴5(a+2b)=9(2a﹣b)
∴5a+10b=18a﹣9b
∴19b=13a
∴a:b=.
15.解:∵点D、E分别是AB、AC边的中点,
∴DE=BC,DE∥BC,
∴△ADE∽△ABC,
∴===,
∵等腰△ABC的面积为4cm2,
∴△ADE的面积是1cm2,
∴梯形DBCE的面积为4﹣1=3(cm2),
故答案为:3.
16.解:∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,
∴正六角星形AFBDCE∽正六角星形A1F1B1D1C1E1,且相似比为2:1,
∵正六角星形AFBDCE的面积为1,
∴正六角星形A1F1B1D1C1E1的面积为,
同理可得,第三个六角星形的面积为:=,
第四个六角星形的面积为:=,
故答案为:.
三.解答题(共4小题,满分40分)
17.解:由题意得:∠CAD=∠MND=90°,∠CDA=∠MDN,
∴△CAD∽△MND,
∴,
∴,
∴MN=9.6(米),
又∵∠EBF=∠MNF=90°,
∠EFB=∠MFN,
∴△EFB∽△MFN,
∴,
∴
∴EB≈1.75(米),
∴小军身高约为1.75米.
18.解:(1)如图,△A1B1C1即为所求,C1(2,﹣2);
(2)如图,△A2BC2即为所求,C2(1,0),
△A2BC2的面积:
6×4﹣×2×6﹣×2×4﹣×2×4
=24﹣6﹣4﹣4
=24﹣14
=10.
19.证明:(1)∵AD=CD,DE⊥AC,
∴DE垂直平分AC,
∴AF=CF,∠DFA=∠DFC=90°,∠DAF=∠DCF.
∵∠DAB=∠DAF+∠CAB=90°,∠CAB+∠B=90°,
∴∠DCF=∠DAF=∠B.
在Rt△DCF和Rt△ABC中,∠DFC=∠ACB=90°,∠DCF=∠B,
∴△DCF∽△ABC.
∴=,即=,
∴AB AF=CB CD;
(2)解:连接PB,
①∵AB=15,BC=9,∠ACB=90°,
∴AC===12,
∴CF=AF=6.
∴y=(x+9)×6=3x+27;
②由EF∥BC,得△AEF∽△ABC.
AE=BE=AB=,EF=.
由∠EAD=∠AFE=90°,∠AEF=∠DEA,得△AEF∽△DEA.
Rt△ADF中,AD=CD==10,AF=6,
∴DF=8.
∴DE=DF+FE=8+=.
∵y=3x+27(0≤x≤),函数值y随着x的增大而增大,
∴当x=时,y有最大值,此时y=.
20.解:(1)存在点P.
假设存在一点P,使点Q与点C重合,如图1所示,设AP的长为x,则BP=10﹣x,
在Rt△APD中,DP2=AD2+AP2,即DP2=42+x2,
在Rt△PBC中,PC2=BC2+PB2,即PC2=42+(10﹣x)2,
在Rt△PCD中,CD2=DP2+PC2,即102=42+x2+42+(10﹣x)2,
解得x=2或8,
故当m=10时,存在点P使得点Q与点C重合,此时AP=2或8;
(2)连接AC,设BP=y,则AP=m﹣y,
∵PQ∥AC,
∴△PBQ∽△ABC,
∴=,即=①,
∵DP⊥PQ,
∴∠APD+∠BPQ=90°,
∵∠APD+∠ADP=90°,∠BPQ+∠PQB=90°,
∴∠APD=∠BQP,
∴△APD∽△BQP,
∴=,即=②,
①②联立得,BQ=;
(3)连接DQ,
由已知PQ⊥PD,所以只有当DP=PQ时,△PQD为等腰三角形(如图),
∴∠BPQ=∠ADP,又∠B=∠A=90°,
∴△PBQ≌△DAP,
∴PB=DA=4,AP=BQ=m﹣4,
∴以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式为:
S四边形PQCD=S矩形ABCD﹣S△DAP﹣S△QBP=4m﹣×4×(m﹣4)﹣×4×(m﹣4)=16(4≤m<8)
当Q在BC延长线上时,S=m2﹣2m(m≥8).
综上所述,S=.
一.选择题(共10小题,满分50分)
1.已知线段a=4,b=16,线段c是a、b的比例中项,那么c等于( )
A.10 B.8 C.﹣8 D.±8
2.如果x:y=2:3,则下列各式不成立的是( )
A. B. C. D.
3.已知线段a、b,求作线段x,使,正确的作法是( )
A. B.
C. D.
4.考虑下面4个命题:①有一个角是100°的两个等腰三角形相似;②斜边和周长对应相等的两个直角三角形全等;③对角线互相垂直且相等的四边形是正方形;④对角线相等的梯形是等腰梯形.其中正确命题的序号是( )
A.①②③④ B.①③④ C.①②④ D.②③④
5.如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )
A.4对 B.5对 C.6对 D.7对
6.如图,在△ABC中,EF∥BC,=,S四边形BCFE=8,则S△ABC=( )
A.9 B.10 C.12 D.13
7.宽与长的比是(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连接EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
A.矩形ABFE B.矩形EFCD C.矩形EFGH D.矩形DCGH
8.如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点P使△PAD和△PBC相似,则这样的点P存在的个数有( )
A.1 B.2 C.3 D.4
9.如图,已知△ABC三个顶点的坐标分别为(1,2),(﹣2,3),(﹣1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点A′,B′,C′.下列说法正确的是( )
A.△A′B′C′与△ABC是位似图形,位似中心是点(1,0)
B.△A′B′C′与△ABC是位似图形,位似中心是点(0,0)
C.△A′B′C′与△ABC是相似图形,但不是位似图形
D.△A′B′C′与△ABC不是相似图形
10.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2020个正方形的面积为( )
A. B. C.5×()2020 D.5×()4038
二.填空题(共6小题,满分30分)
11.已知线段a=4 cm,b=9 cm,则线段a,b的比例中项为 cm.
12.如图,在已建立直角坐标系的4×4的正方形方格纸中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P、A、B为顶点的三角形与△ABC相似(C点除外),则格点P的坐标是 .
13.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上.若线段AB=4cm,则线段BC= cm.
14.已知,则a:b= .
15.如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为 cm2.
16.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分,取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分,如此下去…,则正六角星形A4F4B4D4C4E4的面积为 .
三.解答题(共4小题,满分40分)
17.晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长.(结果精确到0.01米)
18.已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2:1,并直接写出C2点的坐标及△A2BC2的面积.
19.如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.
(1)求证:AB AF=CB CD;
(2)已知AB=15cm,BC=9cm,P是线段DE上的动点.设DP=x cm,梯形BCDP的面积为ycm2.
①求y关于x的函数关系式.
②y是否存在最大值?若有求出这个最大值,若不存在请说明理由.
20.如图,在矩形ABCD中,AD=4cm,AB=m(m>4),点P是AB边上的任意一点(不与点A、B重合),连接PD,过点P作PQ⊥PD,交直线BC于点Q.
(1)当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由;
(2)连接AC,若PQ∥AC,求线段BQ的长(用含m的代数式表示);
(3)若△PQD为等腰三角形,求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式,并写出m的取值范围.
参考答案
一.选择题(共10小题,满分50分)
1.解:∵线段c是a、b的比例中项,
∴c2=ab=64,
解得c=±8,
又∵线段是正数,
∴c=8.
故选:B.
2.解:可设x=2k,y=3k.通过代入计算,
进行约分,A,B,C都正确;
D不能实现约分,故错误.
故选:D.
3.解:由题意,
∴,
∵线段x没法先作出,
∴B选项错误,
根据平行线分线段成比例定理,只有C符合.
故选:C.
4.解:①正确,因为已知一个角为100°和等腰三角形,没有指出该角是顶角还是底角,根据三角形内角和公式得,该角为顶角,又因为是等腰三角形则两腰对应成比例,所以这两个等腰三角形相似;
②正确,因为两个直角三角形的斜边相等,周长对应相等,由于均为直角三角形且周长相等,两直角边长的和及平方和均为定值,知道a+b及a平方+b平方,ab亦确定,而已知a+b,ab均为正的定值,就本题而言,a,b值具有对称性(如一三角形两直角边为3,4则另一三角形两直角边必定也为一个3,一个4),最终两三角形边均对应相等,必定全等;
③错误,因为对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,既是矩形又是菱形的四边形是正方形,所以,对角线互相垂直且相等的平行四边形是正方形;
④正确,可以根据等腰梯形的判定得到.
故选:C.
5.解:图中相似三角形有△ABC∽△CDA,△AGE∽△ABC,△AFE∽△CBE,△BGE∽△BAF,△AGE∽△CDA共5对,
理由是:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,AB=CD,∠D=∠ABC,
∴△ABC≌△CDA,即△ABC∽△CDA,
∵GE∥BC,
∴△AGE∽△ABC∽△CDA,
∵GE∥BC,AD∥BC,
∴GE∥AD,
∴△BGE∽△BAF,
∵AD∥BC,
∴△AFE∽△CBE.
故选:B.
6.解:∵=,
∴==,
∵EF∥BC,
∴△AEF∽△ABC,
∴==,
∴9S△AEF=S△ABC,
∵S四边形BCFE=8,
∴9(S△ABC﹣8)=S△ABC,
解得:S△ABC=9.
故选:A.
7.解:设正方形的边长为2,则CD=2,CF=1
在直角三角形DCF中,DF==
∴FG=
∴CG=﹣1
∴=
∴矩形DCGH为黄金矩形
故选:D.
8.解:∵AD∥BC,∠D=90°
∴∠C=∠D=90°
∵DC=7,AD=2,BC=4
设PD=x,则PC=7﹣x;
①若PD:PC=AD:BC,则△PAD∽△PBC
∴,解得:PD=
②若PD:BC=AD:PC,则△PAD∽△BPC
∴,解得:PD=,
∴这样的点P存在的个数有3个.
故选:C.
9.解:∵△ABC三个顶点的坐标分别为(1,2),(﹣2,3),(﹣1,0),把它们的横坐标和纵坐标都扩大到原来的2倍
∴点A′,B′,C′的坐标分别为(2,4),(﹣4,6),(﹣2,0)
∴直线AA′,BB′,CC′得解析式分别为y=2x,y=﹣x,y=0
∴对应点的连线交于原点
∴△A′B′C′与△ABC是位似图形,位似中心是点(0,0)
故选:B.
10.
解:设正方形的面积分别为S1,S2…S2010,
根据题意,得:AD∥BC∥C1A2∥C2B2,
∴∠BAA1=∠B1A1A2=∠B2A2x(同位角相等).
∵∠ABA1=∠A1B1A2=90°,
∴△BAA1∽△B1A1A2,
在直角△ADO中,根据勾股定理,得:AD=,
∴BA1=AB=,
∴CA1=+=×,
同理,得:C1A2=××,
由正方形的面积公式,得:S1=,
S2=×,S3=××,
由此,可得Sn=×(1+)2n﹣2,
∴S2020=5×()2×2020﹣2,
=5×()4038.
故选:D.
二.填空题(共6小题,满分30分)
11.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
设它们的比例中项是x,则x2=4×9,x=±6,(线段是正数,负值舍去),故填6.
12.解:如图:此时AB对应P1A或P2B,且相似比为1:2,
故点P的坐标为:(1,4)或(3,4);
△ABC≌△BAP3,
此时P的坐标为(3,1);
∴格点P的坐标是(1,4)或(3,1)或(3,4).
13.解:如图,过点A作AE⊥CE于点E,交BD于点D,
∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,
∴,
即,
∴BC=12cm.
故答案为:12.
14.解:∵
∴5(a+2b)=9(2a﹣b)
∴5a+10b=18a﹣9b
∴19b=13a
∴a:b=.
15.解:∵点D、E分别是AB、AC边的中点,
∴DE=BC,DE∥BC,
∴△ADE∽△ABC,
∴===,
∵等腰△ABC的面积为4cm2,
∴△ADE的面积是1cm2,
∴梯形DBCE的面积为4﹣1=3(cm2),
故答案为:3.
16.解:∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,
∴正六角星形AFBDCE∽正六角星形A1F1B1D1C1E1,且相似比为2:1,
∵正六角星形AFBDCE的面积为1,
∴正六角星形A1F1B1D1C1E1的面积为,
同理可得,第三个六角星形的面积为:=,
第四个六角星形的面积为:=,
故答案为:.
三.解答题(共4小题,满分40分)
17.解:由题意得:∠CAD=∠MND=90°,∠CDA=∠MDN,
∴△CAD∽△MND,
∴,
∴,
∴MN=9.6(米),
又∵∠EBF=∠MNF=90°,
∠EFB=∠MFN,
∴△EFB∽△MFN,
∴,
∴
∴EB≈1.75(米),
∴小军身高约为1.75米.
18.解:(1)如图,△A1B1C1即为所求,C1(2,﹣2);
(2)如图,△A2BC2即为所求,C2(1,0),
△A2BC2的面积:
6×4﹣×2×6﹣×2×4﹣×2×4
=24﹣6﹣4﹣4
=24﹣14
=10.
19.证明:(1)∵AD=CD,DE⊥AC,
∴DE垂直平分AC,
∴AF=CF,∠DFA=∠DFC=90°,∠DAF=∠DCF.
∵∠DAB=∠DAF+∠CAB=90°,∠CAB+∠B=90°,
∴∠DCF=∠DAF=∠B.
在Rt△DCF和Rt△ABC中,∠DFC=∠ACB=90°,∠DCF=∠B,
∴△DCF∽△ABC.
∴=,即=,
∴AB AF=CB CD;
(2)解:连接PB,
①∵AB=15,BC=9,∠ACB=90°,
∴AC===12,
∴CF=AF=6.
∴y=(x+9)×6=3x+27;
②由EF∥BC,得△AEF∽△ABC.
AE=BE=AB=,EF=.
由∠EAD=∠AFE=90°,∠AEF=∠DEA,得△AEF∽△DEA.
Rt△ADF中,AD=CD==10,AF=6,
∴DF=8.
∴DE=DF+FE=8+=.
∵y=3x+27(0≤x≤),函数值y随着x的增大而增大,
∴当x=时,y有最大值,此时y=.
20.解:(1)存在点P.
假设存在一点P,使点Q与点C重合,如图1所示,设AP的长为x,则BP=10﹣x,
在Rt△APD中,DP2=AD2+AP2,即DP2=42+x2,
在Rt△PBC中,PC2=BC2+PB2,即PC2=42+(10﹣x)2,
在Rt△PCD中,CD2=DP2+PC2,即102=42+x2+42+(10﹣x)2,
解得x=2或8,
故当m=10时,存在点P使得点Q与点C重合,此时AP=2或8;
(2)连接AC,设BP=y,则AP=m﹣y,
∵PQ∥AC,
∴△PBQ∽△ABC,
∴=,即=①,
∵DP⊥PQ,
∴∠APD+∠BPQ=90°,
∵∠APD+∠ADP=90°,∠BPQ+∠PQB=90°,
∴∠APD=∠BQP,
∴△APD∽△BQP,
∴=,即=②,
①②联立得,BQ=;
(3)连接DQ,
由已知PQ⊥PD,所以只有当DP=PQ时,△PQD为等腰三角形(如图),
∴∠BPQ=∠ADP,又∠B=∠A=90°,
∴△PBQ≌△DAP,
∴PB=DA=4,AP=BQ=m﹣4,
∴以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式为:
S四边形PQCD=S矩形ABCD﹣S△DAP﹣S△QBP=4m﹣×4×(m﹣4)﹣×4×(m﹣4)=16(4≤m<8)
当Q在BC延长线上时,S=m2﹣2m(m≥8).
综上所述,S=.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
