25.5相似三角形的性质 解答题专题训练 2021-2022学年冀教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 25.5相似三角形的性质 解答题专题训练 2021-2022学年冀教版九年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 429.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 11:01:03 | ||
图片预览



文档简介
2021-2022学年冀教版九年级数学上册《25.5相似三角形的性质》解答题专题训练(附答案)
1.如图:AD∥EG∥BC,EG交DB于点F,已知AD=6,BC=8,AE=6,EF=2.
(1)求EB的长;
(2)求FG的长.
2.如图,在△ABC中,D为BC上一点,∠BAD=∠C.
(1)求证:△ABD∽△CBA;
(2)若AB=6,BD=3,求CD的长.
3.如图,在△ABC中,∠C=90°,D是AC边上一点,DE⊥AB于E.若AB=15,BC=9,DE=3.
(1)求AE的长.
(2)求四边形BCDE的面积.
4.如图,四边形ABCD为平行四边形,E为边AD上一点,连接AC、BE,它们相交于点F,且∠ACB=∠ABE.
(1)求证:AE2=EF BE;
(2)若AE=2,EF=1,CF=4,求AB的长.
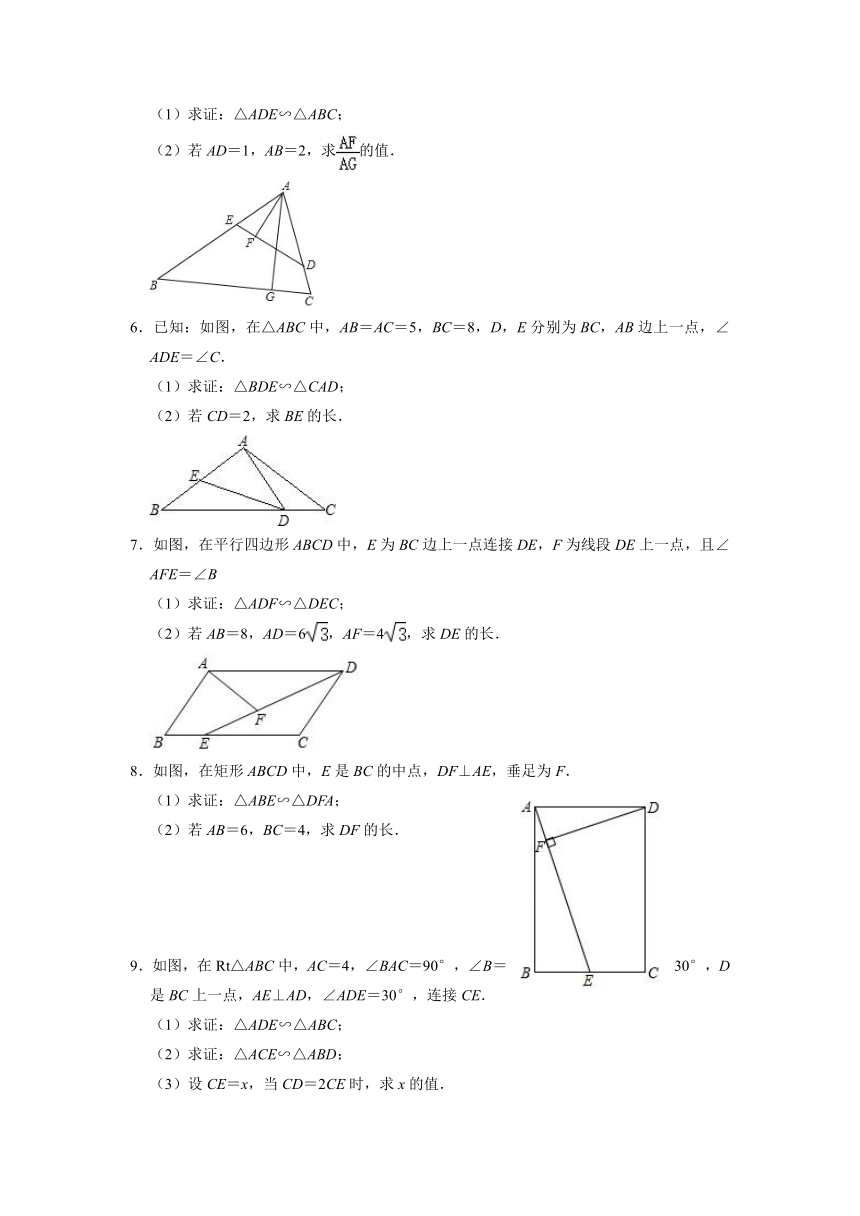
5.如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=1,AB=2,求的值.
6.已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
7.如图,在平行四边形ABCD中,E为BC边上一点连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求DE的长.
8.如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长.
9.如图,在Rt△ABC中,AC=4,∠BAC=90°,∠B=30°,D是BC上一点,AE⊥AD,∠ADE=30°,连接CE.
(1)求证:△ADE∽△ABC;
(2)求证:△ACE∽△ABD;
(3)设CE=x,当CD=2CE时,求x的值.
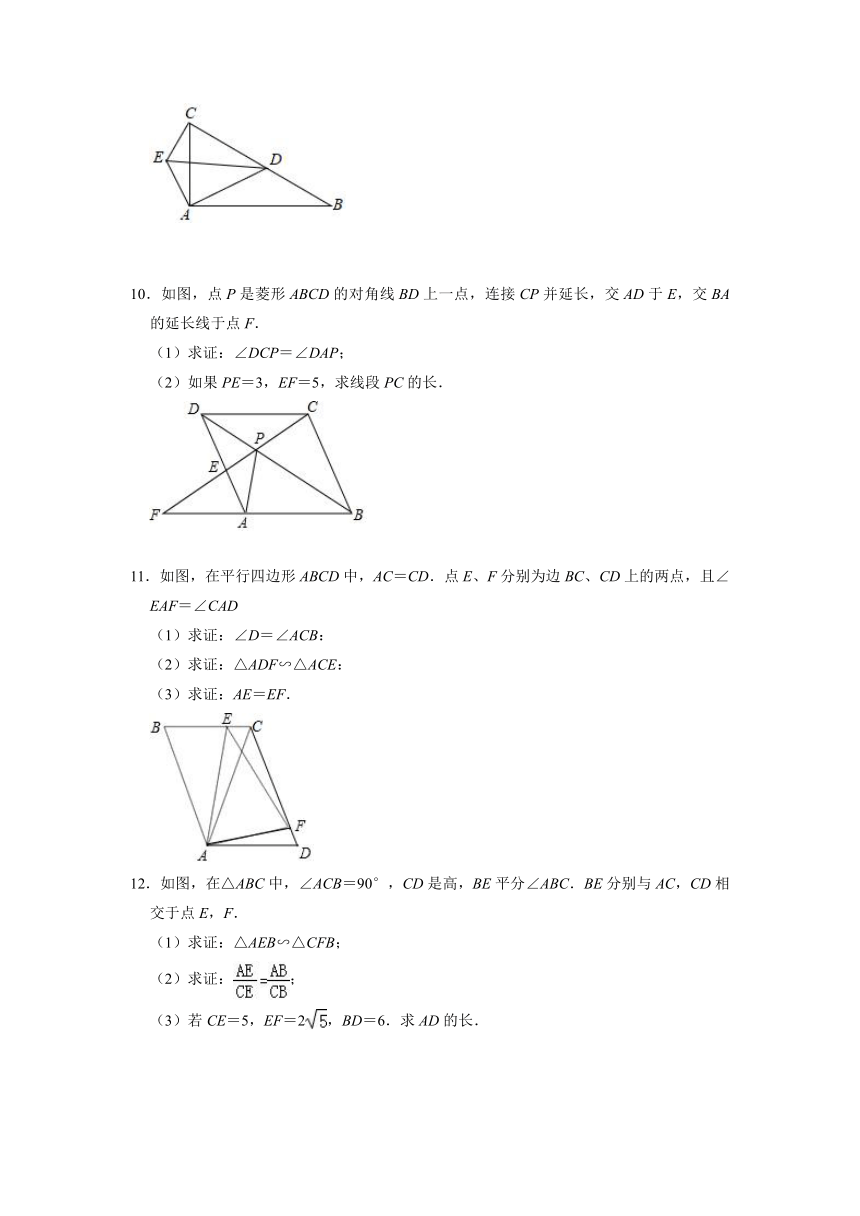
10.如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
(1)求证:∠DCP=∠DAP;
(2)如果PE=3,EF=5,求线段PC的长.
11.如图,在平行四边形ABCD中,AC=CD.点E、F分别为边BC、CD上的两点,且∠EAF=∠CAD
(1)求证:∠D=∠ACB:
(2)求证:△ADF∽△ACE:
(3)求证:AE=EF.
12.如图,在△ABC中,∠ACB=90°,CD是高,BE平分∠ABC.BE分别与AC,CD相交于点E,F.
(1)求证:△AEB∽△CFB;
(2)求证:;
(3)若CE=5,EF=2,BD=6.求AD的长.
13.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:=;
(2)连接DE,求证:DE=CE;
(3)若CD⊥AB,AD=2,BD=3,求线段EG的长.
14.如图,AC是 ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G.
(1)求证:BE2=EF EG;
(2)若2DG=DC,BE=6,求EF的长.
15.如图,在△EAD中,∠EAD=90°,AC是高,B在DE延长线上,且∠BAE=∠EAC.
(1)求证:△ABE∽△DBA;
(2)求证:BD EC=AB AC.
16.如图,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=CE,点D为边BC上一点,GD=GB,连接AD交BE于点F.
(1)求证:∠ABE=∠EAF;
(2)求证:AE2=EF EC;
(3)若CG=2AG,AD=2AF,BC=5,求AE的长.
17.已知:如图,在菱形ABCD中,点E、F分别在BC、CD上,且∠BAE=∠DAF.
(1)如图,若AD=AF,延长AE、DC交于点G,求证:AF2=DG DF.
(2)在第(1)小题的条件下,连接BD,交AG于点H,若HE=4,EG=12,求AH的长.
18.如图,点P是线段BD上一个动点,∠B=∠D=90°,AB=6,CD=4,BD=a.
(1)当∠APC=90°,a=14时,求BP的长度;
(2)若∠APC=90°时,点P有两个符合要求即P1,P2,且P1P2=2,求a的值;
(3)若∠APC=120°时,点P有且只有一个点符合要求,求a的值.
19.如图,已知△ABC中,AC=BC,∠ACB=120°,P为△ABC内部一点,且满足∠APB=∠BPC=150°.
(1)求证:△PAB∽△PBC;
(2)求证:PA=3PC;
(3)若AB=10,求PA的长.
参考答案
1.解:(1)∵EG∥AD,
∴△BAD∽△BEF,
∴=,即=,
∴EB=3.
(2)∵EG∥∥BC,
∴△AEG∽△ABC,
∴=,即=,
∴EG=,
∴FG=EG﹣EF=.
2.证明:(1)∵∠BAD=∠C,∠B=∠B,
∴△ABD∽△CBA;
(2)∵△ABD∽△CBA,
∴,
∵AB=6,BD=3,
∴,
∴BC=12,
∴CD=BC﹣BD=12﹣3=9.
3.解:(1)在△ABC中,∠C=90°,AB=15,BC=9,
∴AC==12,
∵DE⊥AB,
∴∠AED=90°,
∴∠AED=∠C,
又∵∠A=∠A,
∴△ADE∽△ABC,
∴,即,
∴AE=4;
(2)S四边形BCDE=S△ABC﹣S△AED
=×12×9﹣×4×3=48.
4.1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠ACB=∠ABE,
∴∠DAC=∠ABE,
∵∠EAF=∠EBA,∠AEF=∠BEA,
∴△EAF∽△EBA,
∴EA:EB=EF:EA,
∴AE2=EF BE;
(2)∵AE2=EF BE,
∴BE==4,
∴BF=BE﹣EF=4﹣1=3,
∵AE∥BC,
∴=,即=,解得AF=,
∵△EAF∽△EBA,
∴=,即=,
∴AB=.
5.1)证明:∵AG⊥BC于点G,AF⊥DE于点G,
∴∠AEF=∠AGC=90°,
又∠EAF=∠GAC,
∴△AEF∽△ACG①,
∴∠AED=∠ACG,
又∠DAE=∠BAC,
∴△ADE∽△ABC②.
(2)解:由①可得,
由②可得=,
∴.
6.1)证明:∵AB=AC,
∴∠B=∠C.
∵∠ADE+∠BDE=∠ADB=∠C+∠CAD,
∠ADE=∠C,
∴∠BDE=∠CAD.
∴△BDE∽△CAD.
(2)解:由(1)得.
∵AB=AC=5,BC=8,CD=2,
∴DB=BC﹣CD=6.
∴.
7.1)证明:∵四边形ABCD是平行四边形,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)∵四边形ABCD是平行四边形,
∴CD=AB=8,
∵△ADF∽△DEC,
∴,
∴.
8.解:(1)∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠AFD=∠B=90°,
∴△ABE∽△DFA;
(2)∵E是BC的中点,BC=4,
∴BE=2,
∵AB=6,
∴AE=,
∵四边形ABCD是矩形,
∴AD=BC=4,
∵△ABE∽△DFA,
∴,
∴.
9.1)证明:∵AE⊥AD,∠BAC=90°,
∴∠EAD=∠CAB=90°,
∵∠B=30°,∠ADE=30°,
∴∠B=∠ADE,
∴△ADE∽△ABC;
(2)证明:∵∠EAD=∠CAB=90°,
∴∠EAC=∠DAB=90°﹣∠CAD,
∵△ADE∽△ABC,
∴=,
∴=,
∴△ACE∽△ABD;
(3)解:在Rt△ABC中,∠CAB=90°,AC=4,∠B=30°,
∴BC=2AC=8,AB===4,
∵CE=x,CD=2CE,
∴CD=2x,
∵△ACE∽△ABD,
∴=,
∴=,
∴BD=x,
∴BC=CD+BD=2x+x=8,
解得:x=16﹣8.
10.证明:(1)∵四边形ABCD是菱形,
∴AD=CD,∠ADB=∠CDB,CD∥AB,
∵AD=CD,∠ADB=∠CDB,且DP=DP,
∴△ADP≌△CDP(SAS)
∴AP=PC,∠DCP=∠DAP;
(2)∵CD∥AB,
∴∠DCP=∠F,且∠DCP=∠DAP,
∴∠F=∠DAP,且∠APE=∠APF,
∴△APE∽△FPA,
∴,
∴,
∴AP=2,
∴PC=2.
11.证明:(1)∵AC=CD,
∴∠D=∠CAD,
∵四边形ABCD为平行四边形,
∴BC∥AD,
∴∠ACB=∠CAD,
∴∠D=∠ACB;
(2)∵∠EAF=∠CAD,
∴∠EAC=∠DAF,
∴△ADF∽△ACE:
(3)∵△ADF∽△ACE,
∴AD:AC=AF:AE,
∴AD:AF=AC:AE,
∵∠EAF=∠CAD,
∴△EAF∽△CAD,
∴∠EFA=∠D,
∴∠EAF=∠EFA,
∴EA=EF.
12.1)证明:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD为AB边上的高,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠A=∠BCD,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴△AEB∽△CFB.
(2)证明:∵∠ABE=∠CBE,∠A=∠BCD,
∴∠CFE=∠BCD+∠CBE=∠A+∠ABE,
∵∠CEF=∠A+∠ABE,
∴∠CEF=∠CFE,
∴CE=CF,
∵△AEB∽△CFB,
∴=,
∴=.
(3)解:如图,作CH⊥EF于H.
∵CE=CF,CH⊥EF,
∴EH=FH=,
∴CH===2,
由△BFD∽△CFH,
∴=,
∴=,
∴DF=3,CD=CF+DF=8,
由△ACD∽△CBD,
∴=,
∴=,
∴AD=.
13.证明:(1)∵∠ABE=∠ACD,∠A=∠A,
∴△ABE∽△ACD,
∴;
(2)∵,
∴,
又∵∠A=∠A,
∴△ADE∽△ACB,
∴∠AED=∠ABC,
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠ABE+∠CBE,
∵∠ABE=∠ACD,
∴∠CDE=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CDE=∠ABE=∠ACD,
∴DE=CE;
(3)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠A+∠ACD=∠CDE+∠ADE=90°,
∵∠ABE=∠ACD,∠CDE=∠ACD,
∴∠A=∠ADE,∠BEC=∠ABE+∠A=∠A+∠ACD=90°,
∴AE=DE,BE⊥AC,
∵DE=CE,
∴AE=DE=CE,
∴AB=BC,
∵AD=2,BD=3,
∴BC=AB=AD+BD=5,
在Rt△BDC中,CD===4,
在Rt△ADC中,AC===2,
∴DE=AE=CE=,
∵∠ADC=∠GEC=90°,∠ACD=∠GCE,
∴△CGE∽△CAD,
∴,
∴GE===.
14.1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∵AB∥CG,
∴△ABE∽△CGE,
∴=,
∵AF∥BC,
∴△AEF∽△CEB,
∴=,
∴=,
∴BE2=EF EG;
(2)解:∵DF∥BC,
∴===,
∴FG=BF,
设EF=x,则BF=6+x,FG=(6+x),
∵BE2=EF EG;
∴62=x[x+(6+x)],
整理得x2+2x﹣24=0,解得x1=﹣6(舍去),x2=4,
即EF的长为4.
15.解:(1)∵∠EAD=90°,AC⊥BD,
∴∠EAC+∠CAD=∠CAD+∠D=90°,
∴∠EAC=∠D,
∵∠BAE=∠EAC,
∴∠BAE=∠D,
∵∠B=∠B,
∴△ABE∽△DBA;
(2)∵∠EAC=∠D,∠ACE=∠ACD=90°,
∴△AEC∽△DAC,
∴,
由(1)知△ABE∽△DBA,
∴,
∴,
∴BD EC=AB AC.
16.1)证明:∵EB=EC,
∴∠EBC=∠C,
∵AG⊥BD,BG=GD,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠ABD=∠ABE+∠EBC,∠ADB=∠DAC+∠C,
∴∠ABE=∠DAC,
即∠ABE=∠EAF.
(2)证明:∵∠AEF=∠BEA,∠EAF=∠ABE,
∴△AEF∽△BEA,
∴=,
∴AE2=EF EB,
∵EB=EC,
∴AE2=EF EC.
(3)解:设BE交AG于J,连接DJ,DE.
∵AG垂直平分线段BD,
∴JB=JD,
∴∠JBD=∠JDG,
∵∠JBD=∠C,
∴∠JDB=∠C,
∴DJ∥AC,
∴∠AEF=∠DJF,
∵AF=DF,∠AFE=∠DFJ,
∴△AFE≌△DFJ(AAS),
∴EF=FJ,AE=DJ,
∵AF=DF,
∴四边形AJDE是平行四边形,
∴DE∥AG,
∵AG⊥BC,
∴ED⊥BC,
∵EB=EC,
∴BD=DC=,
∴BG=DG=,
∴JG=,
∵∠JGD=90°,
∴DJ===,
∴AE=DJ=.
17.1)证明:∵四边形ABCD是菱形,
∴AB∥DC,
∴∠BAE=∠AGD,
∵∠BAE=∠DAF,
∴∠AGD=∠DAF,
又∵∠ADG=∠FDA,
∴△GAD∽△AFD,
∴,
∴DA2=DG DF,
∵AD=AF,
∴AF2=DG DF;
(2)∵四边形ABCD是菱形,
∴AB∥DC,AD∥BC,
∴△ABH∽△GDH,△AHD∽△EHB,
∴,,
∴,
∴AH2=EH GH,
∵HE=4,EG=12,
∴GH=EG+HE=16,
∴AH2=4×16,
解得AH=8,
即AH的长是8.
18.解:(1)∵∠B=∠D=90°,∠APC=90°,
∴∠A+∠APB=∠CPD+∠APB=90°,
∴∠A=∠CPD,
∴△ABP∽△PDC,
∴=,即=,
解得BP=2或12;
(2)设BP=x,则PD=a﹣x,
由(1)可知△ABP∽△PDC,
∴=,即=,
∴x2﹣ax+24=0,
设方程的两个根为x1,x2,根据根与系数的关系可知x1+x2=a,x1 x2=24,
∵P1P2=2,
∴|x1﹣x2|=2,
∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=4,
∴a2﹣4×24=4,
解得a=±10(负数舍去),
∴a=10;
(3)作∠AEP=∠CFP=120°,
∴∠AEB=∠CFD=60°,
∵AB=6,CD=4,
∴BE=AB=2,DF=CD=,
∴AE=2BE=4,CF=2DF=
∵∠AEP=∠CFP=∠APC=120°,
∴∠EAP=∠CPF,
∴△EPA∽△FCP,
∴=,
设EP=x,则PF=a﹣﹣x,
∴=,
∴x2﹣(a﹣)x+32=0,
∵Δ=0,
∴(a﹣)2﹣4×1×32=0,
∵a>0,
∴a=+8.
19.1)证明:∵△ABC中,AC=BC,∠ACB=120°,
∴∠CAB=∠CBA=(180°﹣120°)=30°,
∴∠1+∠2=30°,
∵∠APB=150°,
∴∠2+∠3=30°,
∴∠3=∠1,
∵∠APB=∠CPB,
∴△PAB∽△PBC.
(2)证明:过点C作CD⊥AB于D.
∵△ABC中,AC=BC,
∴BD=AB,
在Rt△CDB中,∠CBD=30°,
∴=,
∴=,
∴=,
∵△PAB∽△PBC,
∴===,
∴PA=PB,PB=PC,
∴PA= PC=3PC.
(3)解:将线段BP绕点B顺时针旋转60°得到BP′,连接PP′,CP′,则△BPP′为等边三角形,
∴∠4=∠7=60°,PP′=PB=BP′=PC,
∴∠5=∠BPC﹣∠4=150°﹣60°=90°,
在Rt△PP′C中,∠5=90°,PP′=PC,
∴∠6=30°,
∴∠6+∠7=30°+60°=90°,
∴P′C=2PC,
∴在Rt△BCP′中,PPC,由(2)中=,AB=10,可得BC=,
∴(2PC)2+(PC)2=()2,
∴PC=,
∴PA=.
1.如图:AD∥EG∥BC,EG交DB于点F,已知AD=6,BC=8,AE=6,EF=2.
(1)求EB的长;
(2)求FG的长.
2.如图,在△ABC中,D为BC上一点,∠BAD=∠C.
(1)求证:△ABD∽△CBA;
(2)若AB=6,BD=3,求CD的长.
3.如图,在△ABC中,∠C=90°,D是AC边上一点,DE⊥AB于E.若AB=15,BC=9,DE=3.
(1)求AE的长.
(2)求四边形BCDE的面积.
4.如图,四边形ABCD为平行四边形,E为边AD上一点,连接AC、BE,它们相交于点F,且∠ACB=∠ABE.
(1)求证:AE2=EF BE;
(2)若AE=2,EF=1,CF=4,求AB的长.
5.如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=1,AB=2,求的值.
6.已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
7.如图,在平行四边形ABCD中,E为BC边上一点连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求DE的长.
8.如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长.
9.如图,在Rt△ABC中,AC=4,∠BAC=90°,∠B=30°,D是BC上一点,AE⊥AD,∠ADE=30°,连接CE.
(1)求证:△ADE∽△ABC;
(2)求证:△ACE∽△ABD;
(3)设CE=x,当CD=2CE时,求x的值.
10.如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
(1)求证:∠DCP=∠DAP;
(2)如果PE=3,EF=5,求线段PC的长.
11.如图,在平行四边形ABCD中,AC=CD.点E、F分别为边BC、CD上的两点,且∠EAF=∠CAD
(1)求证:∠D=∠ACB:
(2)求证:△ADF∽△ACE:
(3)求证:AE=EF.
12.如图,在△ABC中,∠ACB=90°,CD是高,BE平分∠ABC.BE分别与AC,CD相交于点E,F.
(1)求证:△AEB∽△CFB;
(2)求证:;
(3)若CE=5,EF=2,BD=6.求AD的长.
13.如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点G.
(1)求证:=;
(2)连接DE,求证:DE=CE;
(3)若CD⊥AB,AD=2,BD=3,求线段EG的长.
14.如图,AC是 ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G.
(1)求证:BE2=EF EG;
(2)若2DG=DC,BE=6,求EF的长.
15.如图,在△EAD中,∠EAD=90°,AC是高,B在DE延长线上,且∠BAE=∠EAC.
(1)求证:△ABE∽△DBA;
(2)求证:BD EC=AB AC.
16.如图,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=CE,点D为边BC上一点,GD=GB,连接AD交BE于点F.
(1)求证:∠ABE=∠EAF;
(2)求证:AE2=EF EC;
(3)若CG=2AG,AD=2AF,BC=5,求AE的长.
17.已知:如图,在菱形ABCD中,点E、F分别在BC、CD上,且∠BAE=∠DAF.
(1)如图,若AD=AF,延长AE、DC交于点G,求证:AF2=DG DF.
(2)在第(1)小题的条件下,连接BD,交AG于点H,若HE=4,EG=12,求AH的长.
18.如图,点P是线段BD上一个动点,∠B=∠D=90°,AB=6,CD=4,BD=a.
(1)当∠APC=90°,a=14时,求BP的长度;
(2)若∠APC=90°时,点P有两个符合要求即P1,P2,且P1P2=2,求a的值;
(3)若∠APC=120°时,点P有且只有一个点符合要求,求a的值.
19.如图,已知△ABC中,AC=BC,∠ACB=120°,P为△ABC内部一点,且满足∠APB=∠BPC=150°.
(1)求证:△PAB∽△PBC;
(2)求证:PA=3PC;
(3)若AB=10,求PA的长.
参考答案
1.解:(1)∵EG∥AD,
∴△BAD∽△BEF,
∴=,即=,
∴EB=3.
(2)∵EG∥∥BC,
∴△AEG∽△ABC,
∴=,即=,
∴EG=,
∴FG=EG﹣EF=.
2.证明:(1)∵∠BAD=∠C,∠B=∠B,
∴△ABD∽△CBA;
(2)∵△ABD∽△CBA,
∴,
∵AB=6,BD=3,
∴,
∴BC=12,
∴CD=BC﹣BD=12﹣3=9.
3.解:(1)在△ABC中,∠C=90°,AB=15,BC=9,
∴AC==12,
∵DE⊥AB,
∴∠AED=90°,
∴∠AED=∠C,
又∵∠A=∠A,
∴△ADE∽△ABC,
∴,即,
∴AE=4;
(2)S四边形BCDE=S△ABC﹣S△AED
=×12×9﹣×4×3=48.
4.1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵∠ACB=∠ABE,
∴∠DAC=∠ABE,
∵∠EAF=∠EBA,∠AEF=∠BEA,
∴△EAF∽△EBA,
∴EA:EB=EF:EA,
∴AE2=EF BE;
(2)∵AE2=EF BE,
∴BE==4,
∴BF=BE﹣EF=4﹣1=3,
∵AE∥BC,
∴=,即=,解得AF=,
∵△EAF∽△EBA,
∴=,即=,
∴AB=.
5.1)证明:∵AG⊥BC于点G,AF⊥DE于点G,
∴∠AEF=∠AGC=90°,
又∠EAF=∠GAC,
∴△AEF∽△ACG①,
∴∠AED=∠ACG,
又∠DAE=∠BAC,
∴△ADE∽△ABC②.
(2)解:由①可得,
由②可得=,
∴.
6.1)证明:∵AB=AC,
∴∠B=∠C.
∵∠ADE+∠BDE=∠ADB=∠C+∠CAD,
∠ADE=∠C,
∴∠BDE=∠CAD.
∴△BDE∽△CAD.
(2)解:由(1)得.
∵AB=AC=5,BC=8,CD=2,
∴DB=BC﹣CD=6.
∴.
7.1)证明:∵四边形ABCD是平行四边形,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)∵四边形ABCD是平行四边形,
∴CD=AB=8,
∵△ADF∽△DEC,
∴,
∴.
8.解:(1)∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠AFD=∠B=90°,
∴△ABE∽△DFA;
(2)∵E是BC的中点,BC=4,
∴BE=2,
∵AB=6,
∴AE=,
∵四边形ABCD是矩形,
∴AD=BC=4,
∵△ABE∽△DFA,
∴,
∴.
9.1)证明:∵AE⊥AD,∠BAC=90°,
∴∠EAD=∠CAB=90°,
∵∠B=30°,∠ADE=30°,
∴∠B=∠ADE,
∴△ADE∽△ABC;
(2)证明:∵∠EAD=∠CAB=90°,
∴∠EAC=∠DAB=90°﹣∠CAD,
∵△ADE∽△ABC,
∴=,
∴=,
∴△ACE∽△ABD;
(3)解:在Rt△ABC中,∠CAB=90°,AC=4,∠B=30°,
∴BC=2AC=8,AB===4,
∵CE=x,CD=2CE,
∴CD=2x,
∵△ACE∽△ABD,
∴=,
∴=,
∴BD=x,
∴BC=CD+BD=2x+x=8,
解得:x=16﹣8.
10.证明:(1)∵四边形ABCD是菱形,
∴AD=CD,∠ADB=∠CDB,CD∥AB,
∵AD=CD,∠ADB=∠CDB,且DP=DP,
∴△ADP≌△CDP(SAS)
∴AP=PC,∠DCP=∠DAP;
(2)∵CD∥AB,
∴∠DCP=∠F,且∠DCP=∠DAP,
∴∠F=∠DAP,且∠APE=∠APF,
∴△APE∽△FPA,
∴,
∴,
∴AP=2,
∴PC=2.
11.证明:(1)∵AC=CD,
∴∠D=∠CAD,
∵四边形ABCD为平行四边形,
∴BC∥AD,
∴∠ACB=∠CAD,
∴∠D=∠ACB;
(2)∵∠EAF=∠CAD,
∴∠EAC=∠DAF,
∴△ADF∽△ACE:
(3)∵△ADF∽△ACE,
∴AD:AC=AF:AE,
∴AD:AF=AC:AE,
∵∠EAF=∠CAD,
∴△EAF∽△CAD,
∴∠EFA=∠D,
∴∠EAF=∠EFA,
∴EA=EF.
12.1)证明:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD为AB边上的高,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠A=∠BCD,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴△AEB∽△CFB.
(2)证明:∵∠ABE=∠CBE,∠A=∠BCD,
∴∠CFE=∠BCD+∠CBE=∠A+∠ABE,
∵∠CEF=∠A+∠ABE,
∴∠CEF=∠CFE,
∴CE=CF,
∵△AEB∽△CFB,
∴=,
∴=.
(3)解:如图,作CH⊥EF于H.
∵CE=CF,CH⊥EF,
∴EH=FH=,
∴CH===2,
由△BFD∽△CFH,
∴=,
∴=,
∴DF=3,CD=CF+DF=8,
由△ACD∽△CBD,
∴=,
∴=,
∴AD=.
13.证明:(1)∵∠ABE=∠ACD,∠A=∠A,
∴△ABE∽△ACD,
∴;
(2)∵,
∴,
又∵∠A=∠A,
∴△ADE∽△ACB,
∴∠AED=∠ABC,
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠ABE+∠CBE,
∵∠ABE=∠ACD,
∴∠CDE=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CDE=∠ABE=∠ACD,
∴DE=CE;
(3)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠A+∠ACD=∠CDE+∠ADE=90°,
∵∠ABE=∠ACD,∠CDE=∠ACD,
∴∠A=∠ADE,∠BEC=∠ABE+∠A=∠A+∠ACD=90°,
∴AE=DE,BE⊥AC,
∵DE=CE,
∴AE=DE=CE,
∴AB=BC,
∵AD=2,BD=3,
∴BC=AB=AD+BD=5,
在Rt△BDC中,CD===4,
在Rt△ADC中,AC===2,
∴DE=AE=CE=,
∵∠ADC=∠GEC=90°,∠ACD=∠GCE,
∴△CGE∽△CAD,
∴,
∴GE===.
14.1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∵AB∥CG,
∴△ABE∽△CGE,
∴=,
∵AF∥BC,
∴△AEF∽△CEB,
∴=,
∴=,
∴BE2=EF EG;
(2)解:∵DF∥BC,
∴===,
∴FG=BF,
设EF=x,则BF=6+x,FG=(6+x),
∵BE2=EF EG;
∴62=x[x+(6+x)],
整理得x2+2x﹣24=0,解得x1=﹣6(舍去),x2=4,
即EF的长为4.
15.解:(1)∵∠EAD=90°,AC⊥BD,
∴∠EAC+∠CAD=∠CAD+∠D=90°,
∴∠EAC=∠D,
∵∠BAE=∠EAC,
∴∠BAE=∠D,
∵∠B=∠B,
∴△ABE∽△DBA;
(2)∵∠EAC=∠D,∠ACE=∠ACD=90°,
∴△AEC∽△DAC,
∴,
由(1)知△ABE∽△DBA,
∴,
∴,
∴BD EC=AB AC.
16.1)证明:∵EB=EC,
∴∠EBC=∠C,
∵AG⊥BD,BG=GD,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠ABD=∠ABE+∠EBC,∠ADB=∠DAC+∠C,
∴∠ABE=∠DAC,
即∠ABE=∠EAF.
(2)证明:∵∠AEF=∠BEA,∠EAF=∠ABE,
∴△AEF∽△BEA,
∴=,
∴AE2=EF EB,
∵EB=EC,
∴AE2=EF EC.
(3)解:设BE交AG于J,连接DJ,DE.
∵AG垂直平分线段BD,
∴JB=JD,
∴∠JBD=∠JDG,
∵∠JBD=∠C,
∴∠JDB=∠C,
∴DJ∥AC,
∴∠AEF=∠DJF,
∵AF=DF,∠AFE=∠DFJ,
∴△AFE≌△DFJ(AAS),
∴EF=FJ,AE=DJ,
∵AF=DF,
∴四边形AJDE是平行四边形,
∴DE∥AG,
∵AG⊥BC,
∴ED⊥BC,
∵EB=EC,
∴BD=DC=,
∴BG=DG=,
∴JG=,
∵∠JGD=90°,
∴DJ===,
∴AE=DJ=.
17.1)证明:∵四边形ABCD是菱形,
∴AB∥DC,
∴∠BAE=∠AGD,
∵∠BAE=∠DAF,
∴∠AGD=∠DAF,
又∵∠ADG=∠FDA,
∴△GAD∽△AFD,
∴,
∴DA2=DG DF,
∵AD=AF,
∴AF2=DG DF;
(2)∵四边形ABCD是菱形,
∴AB∥DC,AD∥BC,
∴△ABH∽△GDH,△AHD∽△EHB,
∴,,
∴,
∴AH2=EH GH,
∵HE=4,EG=12,
∴GH=EG+HE=16,
∴AH2=4×16,
解得AH=8,
即AH的长是8.
18.解:(1)∵∠B=∠D=90°,∠APC=90°,
∴∠A+∠APB=∠CPD+∠APB=90°,
∴∠A=∠CPD,
∴△ABP∽△PDC,
∴=,即=,
解得BP=2或12;
(2)设BP=x,则PD=a﹣x,
由(1)可知△ABP∽△PDC,
∴=,即=,
∴x2﹣ax+24=0,
设方程的两个根为x1,x2,根据根与系数的关系可知x1+x2=a,x1 x2=24,
∵P1P2=2,
∴|x1﹣x2|=2,
∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=4,
∴a2﹣4×24=4,
解得a=±10(负数舍去),
∴a=10;
(3)作∠AEP=∠CFP=120°,
∴∠AEB=∠CFD=60°,
∵AB=6,CD=4,
∴BE=AB=2,DF=CD=,
∴AE=2BE=4,CF=2DF=
∵∠AEP=∠CFP=∠APC=120°,
∴∠EAP=∠CPF,
∴△EPA∽△FCP,
∴=,
设EP=x,则PF=a﹣﹣x,
∴=,
∴x2﹣(a﹣)x+32=0,
∵Δ=0,
∴(a﹣)2﹣4×1×32=0,
∵a>0,
∴a=+8.
19.1)证明:∵△ABC中,AC=BC,∠ACB=120°,
∴∠CAB=∠CBA=(180°﹣120°)=30°,
∴∠1+∠2=30°,
∵∠APB=150°,
∴∠2+∠3=30°,
∴∠3=∠1,
∵∠APB=∠CPB,
∴△PAB∽△PBC.
(2)证明:过点C作CD⊥AB于D.
∵△ABC中,AC=BC,
∴BD=AB,
在Rt△CDB中,∠CBD=30°,
∴=,
∴=,
∴=,
∵△PAB∽△PBC,
∴===,
∴PA=PB,PB=PC,
∴PA= PC=3PC.
(3)解:将线段BP绕点B顺时针旋转60°得到BP′,连接PP′,CP′,则△BPP′为等边三角形,
∴∠4=∠7=60°,PP′=PB=BP′=PC,
∴∠5=∠BPC﹣∠4=150°﹣60°=90°,
在Rt△PP′C中,∠5=90°,PP′=PC,
∴∠6=30°,
∴∠6+∠7=30°+60°=90°,
∴P′C=2PC,
∴在Rt△BCP′中,PPC,由(2)中=,AB=10,可得BC=,
∴(2PC)2+(PC)2=()2,
∴PC=,
∴PA=.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
