25.5相似三角形的性质 选择专题训练 2021-2022学年冀教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 25.5相似三角形的性质 选择专题训练 2021-2022学年冀教版九年级数学上册(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 737.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 11:01:46 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学上册《25.5相似三角形的性质》选择题专题训练(附答案)
一.选择题
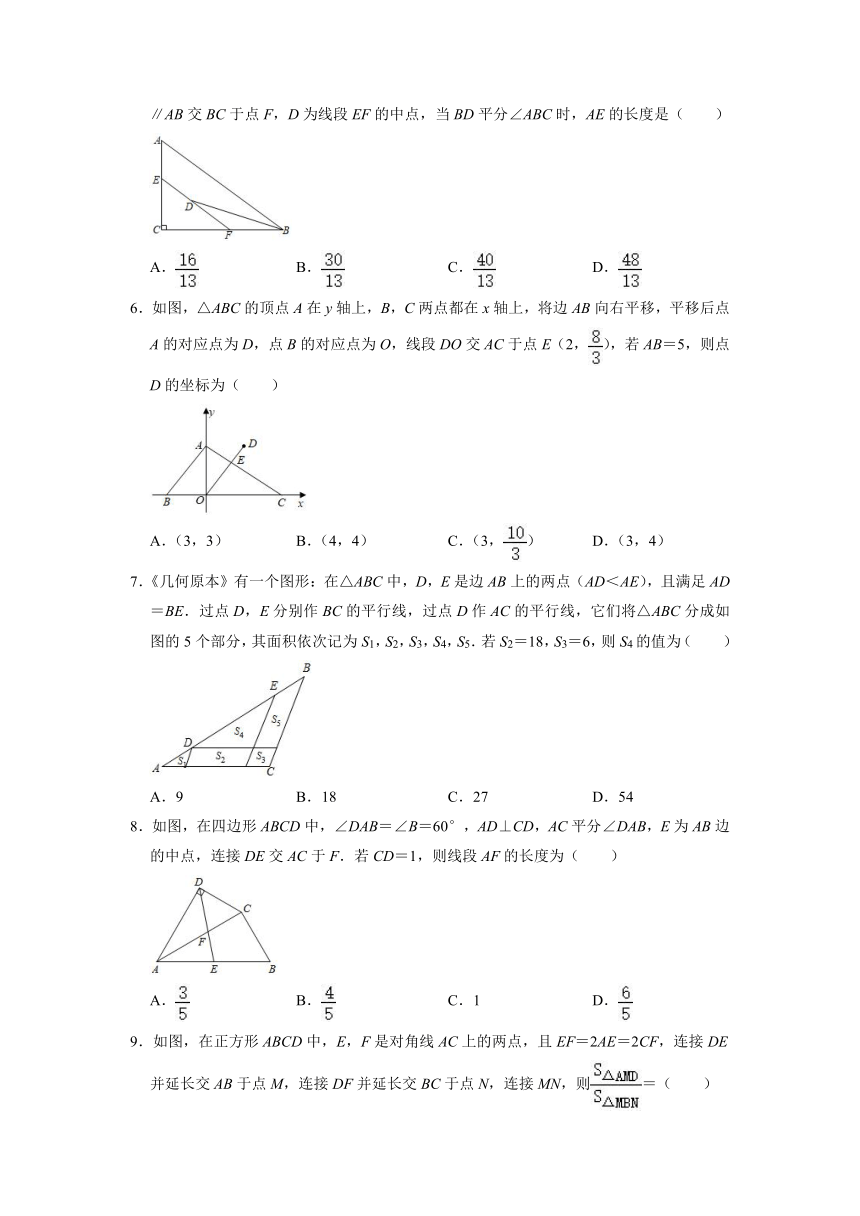
1.如图,在菱形ABCD中,点E、F分别是AB、AD的中点,连接EF交对角线AC于点M,连接BM.若∠BAD=120°,AE=2,则BM的长为( )
A. B.2 C.4 D.3
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,正方形CDEF的顶点E在线段AD上,G是边EF上一点,连接AG,记△AEG面积为S1,△CBD面积为S2,若EG=BD,S1+S2=16,则DE的长为( )
A. B. C.4 D.8
3.如图,正方形ABCD的边AB=3,对角线AC和BD交于点O,P是边CD上靠近点D的三等分点,连接PA,PB,分别交BD,AC于点M,N,连接MN.有下列结论:①OM=MD;②;③MN=;④S△MDP=,其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
4.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④S△AOE:S△BCF=1:2.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,在△ABC中,∠C=90°,AB=10,BC=8.E是AC边上一动点,过点E作EF∥AB交BC于点F,D为线段EF的中点,当BD平分∠ABC时,AE的长度是( )
A. B. C. D.
6.如图,△ABC的顶点A在y轴上,B,C两点都在x轴上,将边AB向右平移,平移后点A的对应点为D,点B的对应点为O,线段DO交AC于点E(2,),若AB=5,则点D的坐标为( )
A.(3,3) B.(4,4) C.(3,) D.(3,4)
7.《几何原本》有一个图形:在△ABC中,D,E是边AB上的两点(AD<AE),且满足AD=BE.过点D,E分别作BC的平行线,过点D作AC的平行线,它们将△ABC分成如图的5个部分,其面积依次记为S1,S2,S3,S4,S5.若S2=18,S3=6,则S4的值为( )
A.9 B.18 C.27 D.54
8.如图,在四边形ABCD中,∠DAB=∠B=60°,AD⊥CD,AC平分∠DAB,E为AB边的中点,连接DE交AC于F.若CD=1,则线段AF的长度为( )
A. B. C.1 D.
9.如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则=( )
A. B. C.1 D.
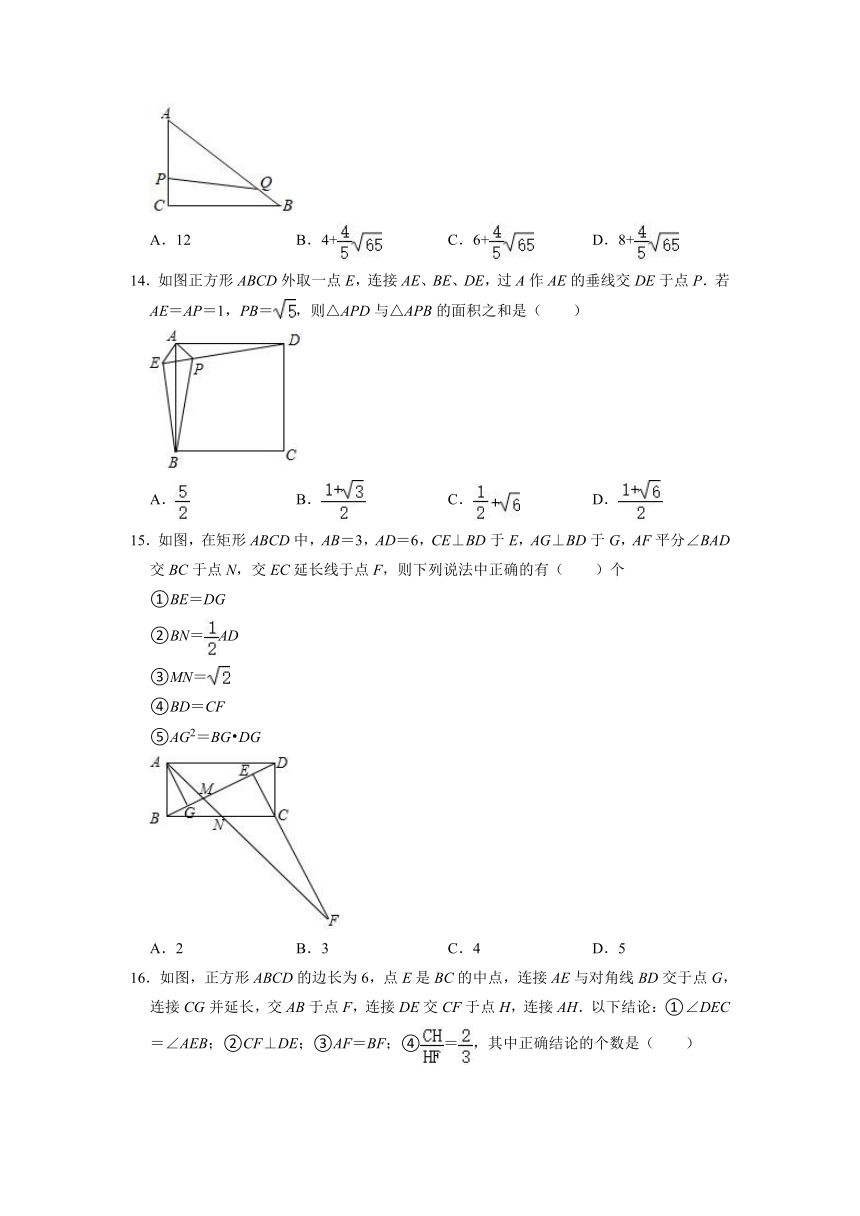
10.如图,在矩形ABCD中,BC=AB,E为BC中点,连接AE交BD于点F,连CF,下列结论:①AE⊥BD;②S矩形ABCD=10S△CEF;③BC2=2DO DF;④=.正确的有( )个.
A.1 B.2 C.3 D.4
11.如图,在Rt△ABC中,∠ACB=90°,分别以其三边为边向外作正方形,延长EA交BG于点M,连接IM交AB于点N,若M是BG的中点,则的值为( )
A. B. C. D.
12.如图正方形ABCD,BE=EF=FC,CG=2GD,BG分别交AE、AF于M、N,下列结论:①AF⊥BG;②;③S四边形CGNF=S△ABN;④.其中正确的有( )
A.①②③ B.②③④ C.①②④ D.①③④
13.如图,在△ABC中,∠ACB=90°,AC=3、BC=4、P、Q两点分别在AC和AB上.且CP=BQ=1,在平面上找一点M.以A、P、Q、M为顶点画平行四边形,这个平行四边形的周长的最大值为( )
A.12 B.4+ C.6+ D.8+
14.如图正方形ABCD外取一点E,连接AE、BE、DE,过A作AE的垂线交DE于点P.若AE=AP=1,PB=,则△APD与△APB的面积之和是( )
A. B. C. D.
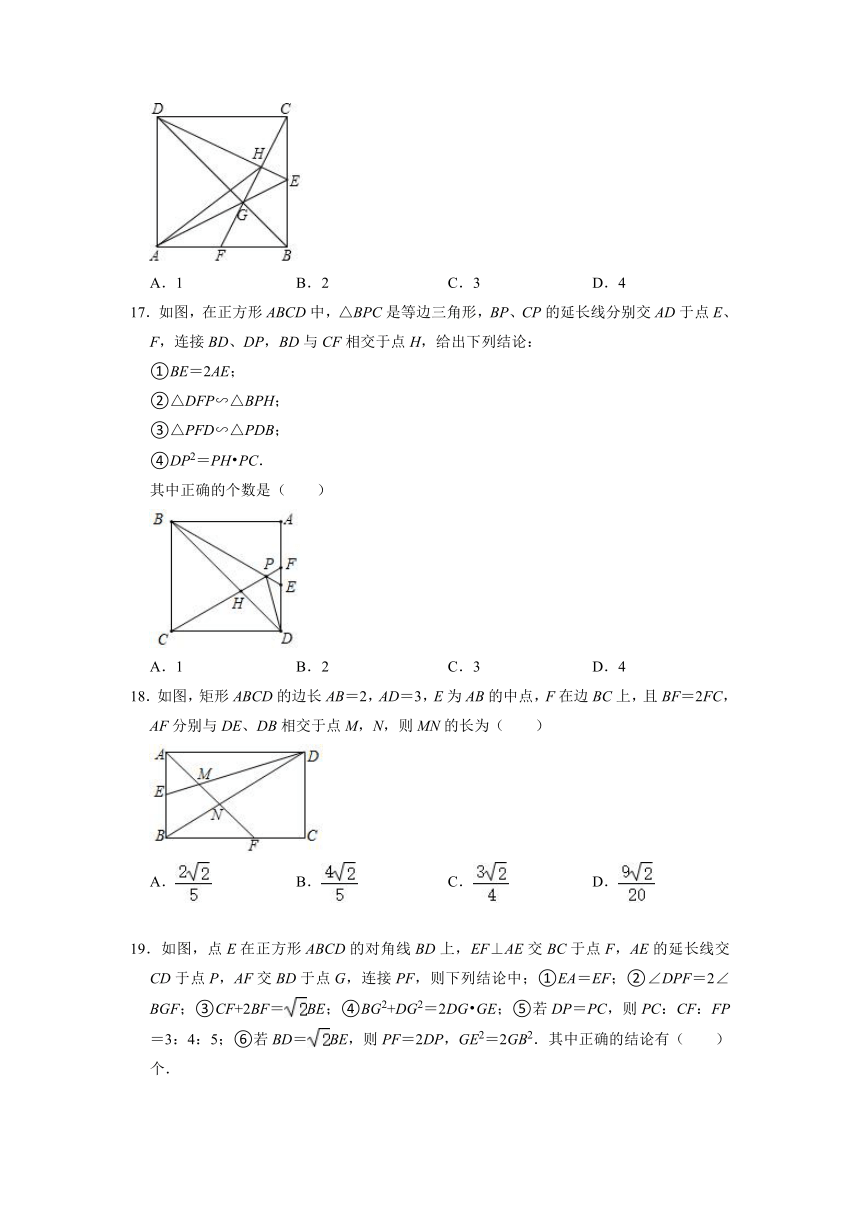
15.如图,在矩形ABCD中,AB=3,AD=6,CE⊥BD于E,AG⊥BD于G,AF平分∠BAD交BC于点N,交EC延长线于点F,则下列说法中正确的有( )个
①BE=DG
②BN=AD
③MN=
④BD=CF
⑤AG2=BG DG
A.2 B.3 C.4 D.5
16.如图,正方形ABCD的边长为6,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①∠DEC=∠AEB;②CF⊥DE;③AF=BF;④=,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
17.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;
②△DFP∽△BPH;
③△PFD∽△PDB;
④DP2=PH PC.
其中正确的个数是( )
A.1 B.2 C.3 D.4
18.如图,矩形ABCD的边长AB=2,AD=3,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A. B. C. D.
19.如图,点E在正方形ABCD的对角线BD上,EF⊥AE交BC于点F,AE的延长线交CD于点P,AF交BD于点G,连接PF,则下列结论中;①EA=EF;②∠DPF=2∠BGF;③CF+2BF=BE;④BG2+DG2=2DG GE;⑤若DP=PC,则PC:CF:FP=3:4:5;⑥若BD=BE,则PF=2DP,GE2=2GB2.其中正确的结论有( )个.
A.6 B.5 C.4 D.3
20.如图在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AC于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②;③△PMN为等边三角形;④当∠ABC=45°时,当BN=BC,其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
21.如图,O是四边形ABCD对角线的交点,已知∠BAD+∠BCA=180°,AB=5,AC=4,AD=3,=,则BC的长为( )
A. B. C. D.
参考答案
1.解:∵四边形ABCD是菱形,
∴AC⊥BD,∠BAC=∠DAC,AB=AD,
∵∠BAD=120°,
∴∠BAC=DAC=∠BAD=60°,
∵点E、F分别为AB、AD的中点,
∴AE=EB,AF=FD,AM=MO,
∵AE=2,
∴AB=2AE=4,
在Rt△AOB中,∠ABO=30°,
∴AO=AB=2,
∴BO==2,
∴MO=AM=AO=1,
在Rt△BOM中,BM==.
故选:A.
2.解:∵CD⊥AB,
∴∠CDB=∠ACB=90°,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴=,
∴CD2=AD BD,
∵四边形CDEF是正方形,
∴CD=DE,
∵△AEG面积=S1=AE EG,△CBD面积=S2=BD CD,且EG=BD,
∴S1+S2=AE EG+BD CD=BD (AE+CD)=BD (AE+ED)=BD AD=CD2=16,
∴CD2=32,
∴CD=4.
∴DE=CD=4.
故选:A.
3.解:∵四边形ABCD是正方形,且正方形的边长为3,
∴AB=BC=CD=AD=3,AB∥CD,AC=BD=3,OA=OB=OC=OD=,
∵P是边CD上靠近点D的三等分点,
∴DP=1,PC=2,
∵AB∥CD,
∴△AMB∽△PMD,
∴,
∴,
∴MB=3DM,且DM+MB=BD=3,
∴DM=,
∴OM=OD﹣DM=,
∴OM=MD,故①正确;
∵AB∥CD,
∴=,
∴AN=CN,
∴AN=,CN=,
∴ON=,
∴S△OMA=××=,S△ONB=×=,
∴,故②正确;
在Rt△MON中,MN===,故③正确;
∵AB∥CD,
∴=3,
∴AM=3MP,
∵S△ADP=×1×3=,且AM=3MP,
∴S△MDP=S△ADP,
∴S△MDP=,故④正确;
综上所述:正确的说法有①②③④.
故选:D.
4.解:连接OD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
在△OBF与△CBF中,
,
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM,
∴①正确;
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴②正确;
∵四边形EBFD是菱形,
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴③正确,
∵△EOB≌△FOB≌△FCB,
∴△EOB≌△CMB错误.
∴②错误;
④∵四边形ABCD是矩形,四边形EBFD是菱形,
∴OA=OC,∠COF=∠AOE,OF=OE,
∴△AOE≌△COF(SAS),
∴S△AOE=S△COF,
∵S△COF=2S△CMF,
∵∠FCO=30°,
∴FM=CM,BM=CM,
∴,
∴S△FOM:S△BOF=1:4,
∵∠OGE=∠OMF,∠GOE=∠MOF,OE=OF,
∴△GEO≌△MFO(AAS),
∴S△GEO=S△MFO,
∴S△DEF=S△EFB=2S△BOF,
设S△EGO=x,则S△AOE=2x,S△BOF=4x,
S四边形DGOF=S△DEF﹣S△EGO=S△EFB﹣S△EGO=8x﹣x,
∴S△AOE:S四边形DGOF=2x:(8x﹣x)=2:7,
故④正确;
所以其中正确结论的个数为3个,
故选:C.
5.解:∵∠C=90°,AB=10,BC=8.
∴AC===6,
∵EF∥AB,
∴∠ABD=∠BDF,又∠ABD=∠FBD,
∴∠FBD=∠BDF,
∴FB=FD,
∴EF=2FB,
∵EF∥AB,
∴△CEF∽△CAB,
∴==,
∴==,
解得,BF=,
∴AE=.
故选:B.
6.解:如图,分别作DF⊥BC垂足为F,EG⊥BC,垂足为G,
∴∠OFE=∠OFD=90°,
∵E(2,),
∴OG=2,GE=,
∵△EOG和△DOF有公共角∠DOF,
∴△EOG∽△DOF,
∴===,
根据平移的性质可知OD=AB=5,
设OF=3x,则DF=4x,
在Rt△ODF中:OD2=DF2+OF2,
即52=(4x)2+(3x)2,
∴x=1或x=﹣1(舍去),
∴OF=3x=3,DF=4x=4.
故D点的坐标为(3,4).
故选:D.
7.解:如图,连接GF,
∵AD=BE,DG∥AC,EF∥BC,
∴===,
∵∠DHE=∠GHF,
∴△DHE∽△GHF,
∴=()2,
∵S2=18,S3=6,
∴=,S△HGF=S3,
∴S△DHE=()2×3=27,
则S4的值为27.
故选:C.
8.解:∵∠DAB=∠B=60°,AC平分∠DAB,
∴∠DAC=∠CAB=30°,
∵AD⊥CD,CD=1,
∴AD=,AC=2,
延长AD、BC交于点G,如图,
∵∠DAB=∠B=60°,
∴∠G=60°,
∴△ABG为等边三角形,
∵AC平分∠DAB,
∴C为GB的中点,且AC⊥GB,
∴AB=,
连接EC,
∵E为AB边的中点,
∴EC=AB=,
∵C为GB的中点,
∴EC∥AD,
∴△EFC∽△DFA,
∴==,
∴AF=AC=.
故选:D.
9.解:设AB=AD=BC=CD=3a,
∵四边形ABCD是正方形,
∴∠DAE=∠DCF=45°,∠DAM=∠DCN=90°,
在△DAE和△DCF中,
,
∴△DAE≌△DCF(SAS),
∴∠ADE=∠CDF,
在△DAM和△DCN中,
,
∴△DAM≌△DCN(ASA),
∴AM=CN,
∵AB=BC,
∴BM=BN,
∵CN∥AD,
∴==,
∴CN=AM=a,BM=BN=2a,
∴===,
故选:A.
10.解:①∵E为BC中点,
∴BE=BC=AB,
∴==,
∵∠ABE=∠DAB,
∴△ABE∽△DAB,
∴∠BEA=∠ABD,
∵∠ABD+∠FBE=90°,
∴∠BEA+∠FBE=90°,
∴∠BFE=90°,
∴AE⊥BD,故①正确;
②过点F作FG⊥BC于点G,如图,
设AB=2a,则BC=2a,BE=a,
∵∠BEA=∠ABD,∠AFB=∠BFE=90°,
∴△FAB∽△BFE,
∴,
设BF=x,则AF=x,
在Rt△ABF中,BF2+AF2=AB2,
即x2+(x)2=(2a)2,
解得:x=a,
∴BF=a,
在Rt△BFE中,由勾股定理得FE==,
∵S△BFE==,
即= FG,
∴FG=a,
∴S△CEF= CE FG==,
S矩形ABCD=2a×2a=4a,
故S矩形ABCD=12S△CEF,故②错误;
③∵AB=2a,BC=2a,
∴BD=2a,
∴DO=×2a=,
∵BF=a,
∴DF=,
∵BC2=(2a)2=8a2,2DO DF=2××=8a2,
∴BC2=2DO DF,故③正确;
④如图,
在Rt△ABE,由勾股定理得AE=a,
∵BF=a,FG=a,
在Rt△BFG,由勾股定理得BG==a,
∴CG=,
在Rt△FGC,由勾股定理得CF==2a,
∴==,故④正确;
故选:C.
11.解:∵四边形AEDC是正方形,
∴∠EAC=∠DCA=90°,EA∥DC,
∴∠MAB=∠CBA,
又∵四边形AFGB是正方形,
∴AB=BG,∠ABG=90°,
∴∠ACB=∠ABM=90°,
∴△ACB∽△MBA,
∴,
又∵M是BG中点,设BM=a,
∴AB=BG=2a,AM=a,
∴AC===,BC=,
∴IA=,
又AE∥DC,IM与BC相交于O,
∴,,
∴CO=AM=,
∴BO=BC﹣OC=﹣=,
∴.
故选:A.
12.解:∵正方形ABCD中,BE=EF=FC,CG=2GD,
∴AB=BC=CD,∠ABC=∠C=90°,
∴BE=EF=FC=BC,BF=BC,CG=CD=BC,
∴BF=CG,
在△ABF和△BCG中,
,
∴△ABF≌△BCG(SAS),
∴∠AFB=∠BGC,
∵∠BGC+∠CBG=90°,
∴∠AFB+∠CBG=90°,
∴∠BNF=90°,
∴AF⊥BG;
故结论①正确.
∵∠BNF=∠C,∠FBN=∠GBC,
∴△BFN∽△BGC,
∴===,
∴BN=NF,
故结论②错误;
∵△ABF≌△BCG,
∴S△ABF=S△BCG,
即:S△ABN+S△BNF=S△BNF+S四边形CGNF,
∴S四边形CGNF=S△ABN,
故结论③正确;
延长AD、BG交于点H,
∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,CG=2GD,BE=BC,
∴△HDG∽△HAB,△BEM∽△HAM,
∴===,=,
∴HG=BH,AH=AD=BC,
∴===,
∴=,
∴BM=BH,
∴MG=BH﹣BM﹣HG=BH﹣BH﹣BH=BH,
∴==.
故结论④正确.
故选:D.
13.解:由勾股定定理得:AB=5,则AQ=4;
过点Q作QN⊥AC,垂足为N,则QN∥BC,
则AN:NC=AQ:QB=4,
则AN=,
∴PN=﹣2=,
由NQ:BC=AQ:AB,得NQ=,
再由勾股定理得:PQ=;
如图1:周长=2(PA+PQ)=4+;
如图2:周长=2(PA+PM)=12;
如图3:周长=2(AQ+PQ)=8+为最长.
故选:D.
14.解:∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∴△APD≌△AEB(SAS),
∴∠APD=∠AEB,
∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴EB⊥ED,
过B作BF⊥AE,交AE的延长线于F,
∵AE=AP,∠EAP=90°,
∴∠AEP=∠APE=45°,
又∵EB⊥ED,BF⊥AF,
∴∠FEB=∠FBE=45°,
∵AE=AP=1,∠EAP=90°,
∴PE=PA=,
又∵BE===
∴BF=EF=BE=,
连接BD,在Rt△AEP中,
∵△APD≌△AEB,
∴PD=BE=,
∵EF=BF=,AE=1,
∴在Rt△ABF中,AB2=(AE+EF)2+BF2=4+,
∴S正方形ABCD=AB2=4+,
∴S△ABP+S△ADP=S△ABD﹣S△BDP=S正方形ABCD﹣×DP×BE=×(4+)﹣××=+,
故选:D.
15.解:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∴∠ABG=∠CDE,
∵CE⊥BD于E,AG⊥BD于G,
∴∠AGB=∠CED=90°,
∴△AGB≌△CED(AAS),
∴BG=DE,
∴BE=DG,故①正确,
∵∠BAD=90°,FA平分∠BAD,
∴∠BAN=45°,
∵∠ABN=90°,
∴∠ANB=45°,
∴AB=BN,
∵AB=3,AD=BC=6,
∴BC=2AB,
∴BN=AD,故②正确,
∵AB=NB=3,
∴AN=3,
∵BN∥AD,
∴==,
∴MN=AN=,故③正确,
连接AC,易证∠ECB=∠BAC,
∵∠ECB=45°+∠F,∠BAC=45°+∠CAF,
∴∠F=∠CAF,
∴CA=CF,
∵四边形ABCD是矩形,
∴AC=BD,
∵BD=CF,故④正确,
∵∠BAD=90°,AG⊥BD,
∴△AGB∽△DGA,可得AG2=BG DG,故⑤正确,
故选:D.
16.解:∵四边形ABCD是边长为6的正方形,点E是BC的中点,
∴AB=AD=BC=CD=6,BE=CE=3,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,
∴△ABE≌△DCE(SAS)
∴∠DEC=∠AEB,∠BAE=∠CDE,DE=AE,故①正确,
∵AB=BC,∠ABG=∠CBG,BG=BG,
∴△ABG≌△CBG(SAS)
∴∠BAE=∠BCF,
∴∠BCF=∠CDE,且∠CDE+∠CED=90°,
∴∠BCF+∠CED=90°,
∴∠CHE=90°,
∴CF⊥DE,故②正确,
∵∠CDE=∠BCF,DC=BC,∠DCE=∠CBF=90°,
∴△DCE≌△CBF(ASA),
∴CE=BF,
∵CE=BC=AB,
∴BF=AB,
∴AF=FB,故③正确,
∵DC=6,CE=3,
∴DE===3,
∵S△DCE=×CD×CE=×DE×CH,
∴CH=,
∵∠CHE=∠CBF,∠BCF=∠ECH,
∴△ECH∽△FCB,
∴=,
∴CF==3,
∴HF=CF﹣CH=,
∴=,故④正确,
故选:D.
17.解:∵四边形ABCD是正方形,
∴∠A=∠CBA=90°,
∵△BCP是等边三角形,
∴∠PBC=∠PCB=∠BPC=60°,
∴∠ABE=30°,
∴BE=2AE,故①正确,
∵AD∥BC,
∴∠DFP=∠BCP=∠BPH=60°,
∵∠PHB=∠PCB+∠CBH=60°+45°=105°,
又∵CD=CP,∠PCD=30°,
∴∠CPD=∠CDP=75°,
∴∠DPF=105°,
∴∠PHB=∠DPF,
∴△DFP∽△BPH,故②正确,
∵∠DPB=60°+75°=135°≠∠DPF,
∴△PFD与△PDB不相似,故③错误,
∵∠PDH=∠PDC﹣∠CDH=75°﹣45°=30°,
∴∠PDH=∠PCD,
∵∠DPH=∠CPD,
∴△PDH∽△PCD,
∴=,
∴PD2=PH PC,故④正确,
故选:C.
18.解:过F作FH⊥AD于H,交ED于O,则FH=AB=2,
∵BF=2FC,BC=AD=3,
∴BF=AH=2,FC=HD=1,
∴AF===2,
∵OH∥AE,
∴==,
∴OH=AE=,
∴OF=FH﹣OH=2﹣=,
∵AE∥FO,
∴△AME∽FMO,
∴==,
∴AM=AF=,
∵AD∥BF,
∴△AND∽△FNB,
∴==,
∴AN=AF=,
∴MN=AN﹣AM=﹣=.
故选:D.
19.证明:①∵AE⊥EF,
∴∠AEF=90°,
∴A、B、F、E四点共圆,
∴∠EAF=∠DBC=45°,
∴AE=EF.
故①正确;
②由①知,∠EAF=45°=∠BDC,
∴A、G、P、D四点共圆.
∴∠AGD=∠APD.
∵∠BGF=∠AGD,
∴∠APD=∠AGD=∠BGF.
延长CD,截DM=BF,连接AM,
∵AD=AB,∠ABC=∠ADM=90°,
∴△ADM≌△ABF(SAS).
∴AM=AF,∠BAF=∠DAM.
∵∠FAP=45°,
∴∠BAF+∠DAP=45°.
∴∠DAM+∠DAP=45°=∠PAM.
∵AP=AP,
∴△AFP≌△AMP(SAS).
∴∠APD=∠APF,PF=PM.
∴∠DPF=2∠APM.
∴∠DPF=2∠BGF.
故②正确;
③作EH⊥BE交BC延长线于H,连CE,如图,
由对称性可知:CE=AE.
∵AE=EF,
∴EF=CE.
∴∠EFC=∠ECF.
∴∠BFE=∠ECH.
∵∠CBD=45°,EH⊥BE,
∴∠EBF=∠H=45°.
∴△BEF≌△HEC(AAS).
∴BF=CH,
∵BH=BE,
∴BF+CF+CH=CF+2BF=BE,
故③正确;
④作DN⊥BD,截DN=BG,连接NG,如图,
则∠ADN=45°=∠ABG,
∵AD=AB,
∴△ABG≌△ADN(SAS).
∴AG=AN,∠BAF=∠DAN.
∵DN⊥BD,
∴DG2+DN2=NG2.
∴BG2+DG2=NG2.
∵∠BAF+∠FAD=90°,
∴∠DAN+∠FAD=90°.
即∠NAF=90°.
∴AG2+AN2=NG2.
∴2AG2=BG2+DG2.
∵∠GAE=∠ADG=45°,∠AGE=∠AGD,
∴△AGE∽△DGA.
∴.
∴AG2=DG EG.
∴BG2+DG2=2DG EG.
故④正确;
⑤由②知:PF=PM=PD+DM,如图,
∴PF=PD+BF.
设CD=BC=6,
∵DP=PC,
∴PC=CD=3.
∴PF=3+BF,CF=6﹣BF.
∵∠C=90°,
∴PF2=CF2+PC2.
∴(3+BF)2=32+(6﹣BF)2.
∴BF=2.
∴CF=4,PF=5.
∴PC:CF:FP=3:4:5.
故⑤正确;
⑥∵BD=BE,BD=AB,
∴BE=AB.
∴∠BAE=∠BEA=(180°﹣45°)÷2=67.5°.
∴∠DAP=22.5°.
∴∠BAF=67.5°﹣45°=22.5°.
∴∠BAF=∠DAP.
∵∠ABF=∠ADP=90°,
∴△BAF≌△DAP(ASA).
∴BF=DP.
由②知:PF=BF+DP,
∴PF=2DP.
在△ABG和△ADE中,
.
∴△ABG≌△ADE(ASA).
∴BG=DE.
作DN⊥BD,截DN=BG,连接NE,AN,如图,
则∠ADN=45°=∠ABG,
∵AD=AB,
∴△ABG≌△ADN(SAS).
∴AG=AN,∠BAF=∠DAN.
在△AGE和△ANE中,
.
∴△AGE≌△ANE(SAS).
∴GE=EN.
∵DN⊥NE,
∴NE2=DE2+NE2.
∴GE2=DE2+BG2.
∴GE2=2BG2.
故⑥正确.
综上所述,①②③④⑤⑥均正确.
故选:A.
20.解:∵BM⊥AC于点M,CN⊥AC于点N,P为BC边的中点,
∴点P是Rt△MBC和Rt△NBC的斜边的中点,
∴MP=NP=BC,
故①正确;
∵BM⊥AC于点M,CN⊥AC于点N,
∴∠AMB=∠ANC=90°,
又∵∠A=∠A,
∴△AMB∽△ANC,
∴=,
故②错误;
∵BM⊥AC于点M,CN⊥AC于点N,P为BC边的中点,
∴点P是Rt△MBC和Rt△NBC的斜边的中点,
∴MP=NP=BP=CP=BC,
∴点M,N,B,C共圆,
∴∠NPM=2∠ABM,
在Rt△ABM中,∠A=60°,
∴∠ABM=30°,
∴∠NPM=60°,
∵PN=PM,
∴△PMN是等边三角形,
故③正确;
当∠ABC=45°时,△BNC为以BC为斜边的等腰直角三角形,
∴BN=BC,
故④正确;
故选:C.
21.解:如图,过D点作AO的平行线,交BA延长线于E点.
∵AO∥ED,
∴=,
即=,
∴AE=,
∵AO∥ED,
∴∠BAC=∠AED,
∵∠BAD+∠BCA=180°,∠BAD+∠EAD=180°,
∴∠BCA=∠EAD,
∴△EAD∽△ACB,
∴=,
∴BC=.
故选:A.
一.选择题
1.如图,在菱形ABCD中,点E、F分别是AB、AD的中点,连接EF交对角线AC于点M,连接BM.若∠BAD=120°,AE=2,则BM的长为( )
A. B.2 C.4 D.3
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,正方形CDEF的顶点E在线段AD上,G是边EF上一点,连接AG,记△AEG面积为S1,△CBD面积为S2,若EG=BD,S1+S2=16,则DE的长为( )
A. B. C.4 D.8
3.如图,正方形ABCD的边AB=3,对角线AC和BD交于点O,P是边CD上靠近点D的三等分点,连接PA,PB,分别交BD,AC于点M,N,连接MN.有下列结论:①OM=MD;②;③MN=;④S△MDP=,其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
4.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④S△AOE:S△BCF=1:2.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,在△ABC中,∠C=90°,AB=10,BC=8.E是AC边上一动点,过点E作EF∥AB交BC于点F,D为线段EF的中点,当BD平分∠ABC时,AE的长度是( )
A. B. C. D.
6.如图,△ABC的顶点A在y轴上,B,C两点都在x轴上,将边AB向右平移,平移后点A的对应点为D,点B的对应点为O,线段DO交AC于点E(2,),若AB=5,则点D的坐标为( )
A.(3,3) B.(4,4) C.(3,) D.(3,4)
7.《几何原本》有一个图形:在△ABC中,D,E是边AB上的两点(AD<AE),且满足AD=BE.过点D,E分别作BC的平行线,过点D作AC的平行线,它们将△ABC分成如图的5个部分,其面积依次记为S1,S2,S3,S4,S5.若S2=18,S3=6,则S4的值为( )
A.9 B.18 C.27 D.54
8.如图,在四边形ABCD中,∠DAB=∠B=60°,AD⊥CD,AC平分∠DAB,E为AB边的中点,连接DE交AC于F.若CD=1,则线段AF的长度为( )
A. B. C.1 D.
9.如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则=( )
A. B. C.1 D.
10.如图,在矩形ABCD中,BC=AB,E为BC中点,连接AE交BD于点F,连CF,下列结论:①AE⊥BD;②S矩形ABCD=10S△CEF;③BC2=2DO DF;④=.正确的有( )个.
A.1 B.2 C.3 D.4
11.如图,在Rt△ABC中,∠ACB=90°,分别以其三边为边向外作正方形,延长EA交BG于点M,连接IM交AB于点N,若M是BG的中点,则的值为( )
A. B. C. D.
12.如图正方形ABCD,BE=EF=FC,CG=2GD,BG分别交AE、AF于M、N,下列结论:①AF⊥BG;②;③S四边形CGNF=S△ABN;④.其中正确的有( )
A.①②③ B.②③④ C.①②④ D.①③④
13.如图,在△ABC中,∠ACB=90°,AC=3、BC=4、P、Q两点分别在AC和AB上.且CP=BQ=1,在平面上找一点M.以A、P、Q、M为顶点画平行四边形,这个平行四边形的周长的最大值为( )
A.12 B.4+ C.6+ D.8+
14.如图正方形ABCD外取一点E,连接AE、BE、DE,过A作AE的垂线交DE于点P.若AE=AP=1,PB=,则△APD与△APB的面积之和是( )
A. B. C. D.
15.如图,在矩形ABCD中,AB=3,AD=6,CE⊥BD于E,AG⊥BD于G,AF平分∠BAD交BC于点N,交EC延长线于点F,则下列说法中正确的有( )个
①BE=DG
②BN=AD
③MN=
④BD=CF
⑤AG2=BG DG
A.2 B.3 C.4 D.5
16.如图,正方形ABCD的边长为6,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①∠DEC=∠AEB;②CF⊥DE;③AF=BF;④=,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
17.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;
②△DFP∽△BPH;
③△PFD∽△PDB;
④DP2=PH PC.
其中正确的个数是( )
A.1 B.2 C.3 D.4
18.如图,矩形ABCD的边长AB=2,AD=3,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A. B. C. D.
19.如图,点E在正方形ABCD的对角线BD上,EF⊥AE交BC于点F,AE的延长线交CD于点P,AF交BD于点G,连接PF,则下列结论中;①EA=EF;②∠DPF=2∠BGF;③CF+2BF=BE;④BG2+DG2=2DG GE;⑤若DP=PC,则PC:CF:FP=3:4:5;⑥若BD=BE,则PF=2DP,GE2=2GB2.其中正确的结论有( )个.
A.6 B.5 C.4 D.3
20.如图在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AC于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②;③△PMN为等边三角形;④当∠ABC=45°时,当BN=BC,其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
21.如图,O是四边形ABCD对角线的交点,已知∠BAD+∠BCA=180°,AB=5,AC=4,AD=3,=,则BC的长为( )
A. B. C. D.
参考答案
1.解:∵四边形ABCD是菱形,
∴AC⊥BD,∠BAC=∠DAC,AB=AD,
∵∠BAD=120°,
∴∠BAC=DAC=∠BAD=60°,
∵点E、F分别为AB、AD的中点,
∴AE=EB,AF=FD,AM=MO,
∵AE=2,
∴AB=2AE=4,
在Rt△AOB中,∠ABO=30°,
∴AO=AB=2,
∴BO==2,
∴MO=AM=AO=1,
在Rt△BOM中,BM==.
故选:A.
2.解:∵CD⊥AB,
∴∠CDB=∠ACB=90°,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴=,
∴CD2=AD BD,
∵四边形CDEF是正方形,
∴CD=DE,
∵△AEG面积=S1=AE EG,△CBD面积=S2=BD CD,且EG=BD,
∴S1+S2=AE EG+BD CD=BD (AE+CD)=BD (AE+ED)=BD AD=CD2=16,
∴CD2=32,
∴CD=4.
∴DE=CD=4.
故选:A.
3.解:∵四边形ABCD是正方形,且正方形的边长为3,
∴AB=BC=CD=AD=3,AB∥CD,AC=BD=3,OA=OB=OC=OD=,
∵P是边CD上靠近点D的三等分点,
∴DP=1,PC=2,
∵AB∥CD,
∴△AMB∽△PMD,
∴,
∴,
∴MB=3DM,且DM+MB=BD=3,
∴DM=,
∴OM=OD﹣DM=,
∴OM=MD,故①正确;
∵AB∥CD,
∴=,
∴AN=CN,
∴AN=,CN=,
∴ON=,
∴S△OMA=××=,S△ONB=×=,
∴,故②正确;
在Rt△MON中,MN===,故③正确;
∵AB∥CD,
∴=3,
∴AM=3MP,
∵S△ADP=×1×3=,且AM=3MP,
∴S△MDP=S△ADP,
∴S△MDP=,故④正确;
综上所述:正确的说法有①②③④.
故选:D.
4.解:连接OD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
在△OBF与△CBF中,
,
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM,
∴①正确;
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴②正确;
∵四边形EBFD是菱形,
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴③正确,
∵△EOB≌△FOB≌△FCB,
∴△EOB≌△CMB错误.
∴②错误;
④∵四边形ABCD是矩形,四边形EBFD是菱形,
∴OA=OC,∠COF=∠AOE,OF=OE,
∴△AOE≌△COF(SAS),
∴S△AOE=S△COF,
∵S△COF=2S△CMF,
∵∠FCO=30°,
∴FM=CM,BM=CM,
∴,
∴S△FOM:S△BOF=1:4,
∵∠OGE=∠OMF,∠GOE=∠MOF,OE=OF,
∴△GEO≌△MFO(AAS),
∴S△GEO=S△MFO,
∴S△DEF=S△EFB=2S△BOF,
设S△EGO=x,则S△AOE=2x,S△BOF=4x,
S四边形DGOF=S△DEF﹣S△EGO=S△EFB﹣S△EGO=8x﹣x,
∴S△AOE:S四边形DGOF=2x:(8x﹣x)=2:7,
故④正确;
所以其中正确结论的个数为3个,
故选:C.
5.解:∵∠C=90°,AB=10,BC=8.
∴AC===6,
∵EF∥AB,
∴∠ABD=∠BDF,又∠ABD=∠FBD,
∴∠FBD=∠BDF,
∴FB=FD,
∴EF=2FB,
∵EF∥AB,
∴△CEF∽△CAB,
∴==,
∴==,
解得,BF=,
∴AE=.
故选:B.
6.解:如图,分别作DF⊥BC垂足为F,EG⊥BC,垂足为G,
∴∠OFE=∠OFD=90°,
∵E(2,),
∴OG=2,GE=,
∵△EOG和△DOF有公共角∠DOF,
∴△EOG∽△DOF,
∴===,
根据平移的性质可知OD=AB=5,
设OF=3x,则DF=4x,
在Rt△ODF中:OD2=DF2+OF2,
即52=(4x)2+(3x)2,
∴x=1或x=﹣1(舍去),
∴OF=3x=3,DF=4x=4.
故D点的坐标为(3,4).
故选:D.
7.解:如图,连接GF,
∵AD=BE,DG∥AC,EF∥BC,
∴===,
∵∠DHE=∠GHF,
∴△DHE∽△GHF,
∴=()2,
∵S2=18,S3=6,
∴=,S△HGF=S3,
∴S△DHE=()2×3=27,
则S4的值为27.
故选:C.
8.解:∵∠DAB=∠B=60°,AC平分∠DAB,
∴∠DAC=∠CAB=30°,
∵AD⊥CD,CD=1,
∴AD=,AC=2,
延长AD、BC交于点G,如图,
∵∠DAB=∠B=60°,
∴∠G=60°,
∴△ABG为等边三角形,
∵AC平分∠DAB,
∴C为GB的中点,且AC⊥GB,
∴AB=,
连接EC,
∵E为AB边的中点,
∴EC=AB=,
∵C为GB的中点,
∴EC∥AD,
∴△EFC∽△DFA,
∴==,
∴AF=AC=.
故选:D.
9.解:设AB=AD=BC=CD=3a,
∵四边形ABCD是正方形,
∴∠DAE=∠DCF=45°,∠DAM=∠DCN=90°,
在△DAE和△DCF中,
,
∴△DAE≌△DCF(SAS),
∴∠ADE=∠CDF,
在△DAM和△DCN中,
,
∴△DAM≌△DCN(ASA),
∴AM=CN,
∵AB=BC,
∴BM=BN,
∵CN∥AD,
∴==,
∴CN=AM=a,BM=BN=2a,
∴===,
故选:A.
10.解:①∵E为BC中点,
∴BE=BC=AB,
∴==,
∵∠ABE=∠DAB,
∴△ABE∽△DAB,
∴∠BEA=∠ABD,
∵∠ABD+∠FBE=90°,
∴∠BEA+∠FBE=90°,
∴∠BFE=90°,
∴AE⊥BD,故①正确;
②过点F作FG⊥BC于点G,如图,
设AB=2a,则BC=2a,BE=a,
∵∠BEA=∠ABD,∠AFB=∠BFE=90°,
∴△FAB∽△BFE,
∴,
设BF=x,则AF=x,
在Rt△ABF中,BF2+AF2=AB2,
即x2+(x)2=(2a)2,
解得:x=a,
∴BF=a,
在Rt△BFE中,由勾股定理得FE==,
∵S△BFE==,
即= FG,
∴FG=a,
∴S△CEF= CE FG==,
S矩形ABCD=2a×2a=4a,
故S矩形ABCD=12S△CEF,故②错误;
③∵AB=2a,BC=2a,
∴BD=2a,
∴DO=×2a=,
∵BF=a,
∴DF=,
∵BC2=(2a)2=8a2,2DO DF=2××=8a2,
∴BC2=2DO DF,故③正确;
④如图,
在Rt△ABE,由勾股定理得AE=a,
∵BF=a,FG=a,
在Rt△BFG,由勾股定理得BG==a,
∴CG=,
在Rt△FGC,由勾股定理得CF==2a,
∴==,故④正确;
故选:C.
11.解:∵四边形AEDC是正方形,
∴∠EAC=∠DCA=90°,EA∥DC,
∴∠MAB=∠CBA,
又∵四边形AFGB是正方形,
∴AB=BG,∠ABG=90°,
∴∠ACB=∠ABM=90°,
∴△ACB∽△MBA,
∴,
又∵M是BG中点,设BM=a,
∴AB=BG=2a,AM=a,
∴AC===,BC=,
∴IA=,
又AE∥DC,IM与BC相交于O,
∴,,
∴CO=AM=,
∴BO=BC﹣OC=﹣=,
∴.
故选:A.
12.解:∵正方形ABCD中,BE=EF=FC,CG=2GD,
∴AB=BC=CD,∠ABC=∠C=90°,
∴BE=EF=FC=BC,BF=BC,CG=CD=BC,
∴BF=CG,
在△ABF和△BCG中,
,
∴△ABF≌△BCG(SAS),
∴∠AFB=∠BGC,
∵∠BGC+∠CBG=90°,
∴∠AFB+∠CBG=90°,
∴∠BNF=90°,
∴AF⊥BG;
故结论①正确.
∵∠BNF=∠C,∠FBN=∠GBC,
∴△BFN∽△BGC,
∴===,
∴BN=NF,
故结论②错误;
∵△ABF≌△BCG,
∴S△ABF=S△BCG,
即:S△ABN+S△BNF=S△BNF+S四边形CGNF,
∴S四边形CGNF=S△ABN,
故结论③正确;
延长AD、BG交于点H,
∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,CG=2GD,BE=BC,
∴△HDG∽△HAB,△BEM∽△HAM,
∴===,=,
∴HG=BH,AH=AD=BC,
∴===,
∴=,
∴BM=BH,
∴MG=BH﹣BM﹣HG=BH﹣BH﹣BH=BH,
∴==.
故结论④正确.
故选:D.
13.解:由勾股定定理得:AB=5,则AQ=4;
过点Q作QN⊥AC,垂足为N,则QN∥BC,
则AN:NC=AQ:QB=4,
则AN=,
∴PN=﹣2=,
由NQ:BC=AQ:AB,得NQ=,
再由勾股定理得:PQ=;
如图1:周长=2(PA+PQ)=4+;
如图2:周长=2(PA+PM)=12;
如图3:周长=2(AQ+PQ)=8+为最长.
故选:D.
14.解:∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∴△APD≌△AEB(SAS),
∴∠APD=∠AEB,
∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴EB⊥ED,
过B作BF⊥AE,交AE的延长线于F,
∵AE=AP,∠EAP=90°,
∴∠AEP=∠APE=45°,
又∵EB⊥ED,BF⊥AF,
∴∠FEB=∠FBE=45°,
∵AE=AP=1,∠EAP=90°,
∴PE=PA=,
又∵BE===
∴BF=EF=BE=,
连接BD,在Rt△AEP中,
∵△APD≌△AEB,
∴PD=BE=,
∵EF=BF=,AE=1,
∴在Rt△ABF中,AB2=(AE+EF)2+BF2=4+,
∴S正方形ABCD=AB2=4+,
∴S△ABP+S△ADP=S△ABD﹣S△BDP=S正方形ABCD﹣×DP×BE=×(4+)﹣××=+,
故选:D.
15.解:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∴∠ABG=∠CDE,
∵CE⊥BD于E,AG⊥BD于G,
∴∠AGB=∠CED=90°,
∴△AGB≌△CED(AAS),
∴BG=DE,
∴BE=DG,故①正确,
∵∠BAD=90°,FA平分∠BAD,
∴∠BAN=45°,
∵∠ABN=90°,
∴∠ANB=45°,
∴AB=BN,
∵AB=3,AD=BC=6,
∴BC=2AB,
∴BN=AD,故②正确,
∵AB=NB=3,
∴AN=3,
∵BN∥AD,
∴==,
∴MN=AN=,故③正确,
连接AC,易证∠ECB=∠BAC,
∵∠ECB=45°+∠F,∠BAC=45°+∠CAF,
∴∠F=∠CAF,
∴CA=CF,
∵四边形ABCD是矩形,
∴AC=BD,
∵BD=CF,故④正确,
∵∠BAD=90°,AG⊥BD,
∴△AGB∽△DGA,可得AG2=BG DG,故⑤正确,
故选:D.
16.解:∵四边形ABCD是边长为6的正方形,点E是BC的中点,
∴AB=AD=BC=CD=6,BE=CE=3,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,
∴△ABE≌△DCE(SAS)
∴∠DEC=∠AEB,∠BAE=∠CDE,DE=AE,故①正确,
∵AB=BC,∠ABG=∠CBG,BG=BG,
∴△ABG≌△CBG(SAS)
∴∠BAE=∠BCF,
∴∠BCF=∠CDE,且∠CDE+∠CED=90°,
∴∠BCF+∠CED=90°,
∴∠CHE=90°,
∴CF⊥DE,故②正确,
∵∠CDE=∠BCF,DC=BC,∠DCE=∠CBF=90°,
∴△DCE≌△CBF(ASA),
∴CE=BF,
∵CE=BC=AB,
∴BF=AB,
∴AF=FB,故③正确,
∵DC=6,CE=3,
∴DE===3,
∵S△DCE=×CD×CE=×DE×CH,
∴CH=,
∵∠CHE=∠CBF,∠BCF=∠ECH,
∴△ECH∽△FCB,
∴=,
∴CF==3,
∴HF=CF﹣CH=,
∴=,故④正确,
故选:D.
17.解:∵四边形ABCD是正方形,
∴∠A=∠CBA=90°,
∵△BCP是等边三角形,
∴∠PBC=∠PCB=∠BPC=60°,
∴∠ABE=30°,
∴BE=2AE,故①正确,
∵AD∥BC,
∴∠DFP=∠BCP=∠BPH=60°,
∵∠PHB=∠PCB+∠CBH=60°+45°=105°,
又∵CD=CP,∠PCD=30°,
∴∠CPD=∠CDP=75°,
∴∠DPF=105°,
∴∠PHB=∠DPF,
∴△DFP∽△BPH,故②正确,
∵∠DPB=60°+75°=135°≠∠DPF,
∴△PFD与△PDB不相似,故③错误,
∵∠PDH=∠PDC﹣∠CDH=75°﹣45°=30°,
∴∠PDH=∠PCD,
∵∠DPH=∠CPD,
∴△PDH∽△PCD,
∴=,
∴PD2=PH PC,故④正确,
故选:C.
18.解:过F作FH⊥AD于H,交ED于O,则FH=AB=2,
∵BF=2FC,BC=AD=3,
∴BF=AH=2,FC=HD=1,
∴AF===2,
∵OH∥AE,
∴==,
∴OH=AE=,
∴OF=FH﹣OH=2﹣=,
∵AE∥FO,
∴△AME∽FMO,
∴==,
∴AM=AF=,
∵AD∥BF,
∴△AND∽△FNB,
∴==,
∴AN=AF=,
∴MN=AN﹣AM=﹣=.
故选:D.
19.证明:①∵AE⊥EF,
∴∠AEF=90°,
∴A、B、F、E四点共圆,
∴∠EAF=∠DBC=45°,
∴AE=EF.
故①正确;
②由①知,∠EAF=45°=∠BDC,
∴A、G、P、D四点共圆.
∴∠AGD=∠APD.
∵∠BGF=∠AGD,
∴∠APD=∠AGD=∠BGF.
延长CD,截DM=BF,连接AM,
∵AD=AB,∠ABC=∠ADM=90°,
∴△ADM≌△ABF(SAS).
∴AM=AF,∠BAF=∠DAM.
∵∠FAP=45°,
∴∠BAF+∠DAP=45°.
∴∠DAM+∠DAP=45°=∠PAM.
∵AP=AP,
∴△AFP≌△AMP(SAS).
∴∠APD=∠APF,PF=PM.
∴∠DPF=2∠APM.
∴∠DPF=2∠BGF.
故②正确;
③作EH⊥BE交BC延长线于H,连CE,如图,
由对称性可知:CE=AE.
∵AE=EF,
∴EF=CE.
∴∠EFC=∠ECF.
∴∠BFE=∠ECH.
∵∠CBD=45°,EH⊥BE,
∴∠EBF=∠H=45°.
∴△BEF≌△HEC(AAS).
∴BF=CH,
∵BH=BE,
∴BF+CF+CH=CF+2BF=BE,
故③正确;
④作DN⊥BD,截DN=BG,连接NG,如图,
则∠ADN=45°=∠ABG,
∵AD=AB,
∴△ABG≌△ADN(SAS).
∴AG=AN,∠BAF=∠DAN.
∵DN⊥BD,
∴DG2+DN2=NG2.
∴BG2+DG2=NG2.
∵∠BAF+∠FAD=90°,
∴∠DAN+∠FAD=90°.
即∠NAF=90°.
∴AG2+AN2=NG2.
∴2AG2=BG2+DG2.
∵∠GAE=∠ADG=45°,∠AGE=∠AGD,
∴△AGE∽△DGA.
∴.
∴AG2=DG EG.
∴BG2+DG2=2DG EG.
故④正确;
⑤由②知:PF=PM=PD+DM,如图,
∴PF=PD+BF.
设CD=BC=6,
∵DP=PC,
∴PC=CD=3.
∴PF=3+BF,CF=6﹣BF.
∵∠C=90°,
∴PF2=CF2+PC2.
∴(3+BF)2=32+(6﹣BF)2.
∴BF=2.
∴CF=4,PF=5.
∴PC:CF:FP=3:4:5.
故⑤正确;
⑥∵BD=BE,BD=AB,
∴BE=AB.
∴∠BAE=∠BEA=(180°﹣45°)÷2=67.5°.
∴∠DAP=22.5°.
∴∠BAF=67.5°﹣45°=22.5°.
∴∠BAF=∠DAP.
∵∠ABF=∠ADP=90°,
∴△BAF≌△DAP(ASA).
∴BF=DP.
由②知:PF=BF+DP,
∴PF=2DP.
在△ABG和△ADE中,
.
∴△ABG≌△ADE(ASA).
∴BG=DE.
作DN⊥BD,截DN=BG,连接NE,AN,如图,
则∠ADN=45°=∠ABG,
∵AD=AB,
∴△ABG≌△ADN(SAS).
∴AG=AN,∠BAF=∠DAN.
在△AGE和△ANE中,
.
∴△AGE≌△ANE(SAS).
∴GE=EN.
∵DN⊥NE,
∴NE2=DE2+NE2.
∴GE2=DE2+BG2.
∴GE2=2BG2.
故⑥正确.
综上所述,①②③④⑤⑥均正确.
故选:A.
20.解:∵BM⊥AC于点M,CN⊥AC于点N,P为BC边的中点,
∴点P是Rt△MBC和Rt△NBC的斜边的中点,
∴MP=NP=BC,
故①正确;
∵BM⊥AC于点M,CN⊥AC于点N,
∴∠AMB=∠ANC=90°,
又∵∠A=∠A,
∴△AMB∽△ANC,
∴=,
故②错误;
∵BM⊥AC于点M,CN⊥AC于点N,P为BC边的中点,
∴点P是Rt△MBC和Rt△NBC的斜边的中点,
∴MP=NP=BP=CP=BC,
∴点M,N,B,C共圆,
∴∠NPM=2∠ABM,
在Rt△ABM中,∠A=60°,
∴∠ABM=30°,
∴∠NPM=60°,
∵PN=PM,
∴△PMN是等边三角形,
故③正确;
当∠ABC=45°时,△BNC为以BC为斜边的等腰直角三角形,
∴BN=BC,
故④正确;
故选:C.
21.解:如图,过D点作AO的平行线,交BA延长线于E点.
∵AO∥ED,
∴=,
即=,
∴AE=,
∵AO∥ED,
∴∠BAC=∠AED,
∵∠BAD+∠BCA=180°,∠BAD+∠EAD=180°,
∴∠BCA=∠EAD,
∴△EAD∽△ACB,
∴=,
∴BC=.
故选:A.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
