25.4相似三角形的判定 同步达标测评 2021-2022学年冀教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 25.4相似三角形的判定 同步达标测评 2021-2022学年冀教版九年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 664.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 11:03:55 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学上册《25.4相似三角形的判定》同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.如图所示,直线y=x﹣1与x轴交于A,与y轴交于B,在第一象限内找点C,使△AOC与△AOB相似,则共能找到的点C的个数( )
A.1 B.2 C.3 D.4
2.如图,在四边形ABCD中,已知∠ADC=∠BAC,那么补充下列条件后不能判定△ADC和△BAC相似的是( )
A.CA平分∠BCD B. C.AC2=BC CD D.∠DAC=∠ABC
3.如图,△ABC中,CE⊥AB,垂足为E,BD⊥AC,垂足为点D,CE与BD交于点F,则图中相似三角形有几对( )
A.6对 B.5对 C.4对 D.3对
4.如图,△ABC中,D、E两点分别在BC、AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F.则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
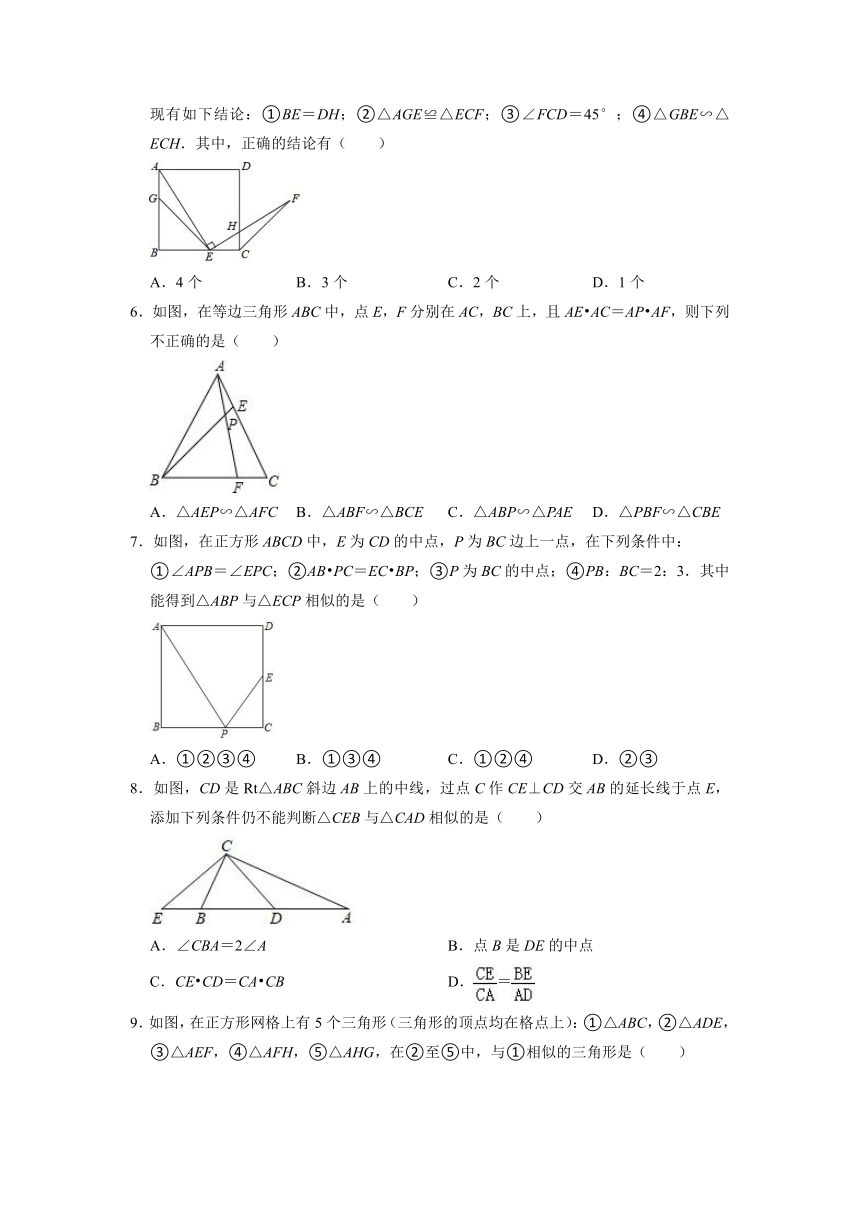
5.如图,G,E分别是正方形ABCD的边AB,BC上的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=DH;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH.其中,正确的结论有( )
A.4个 B.3个 C.2个 D.1个
6.如图,在等边三角形ABC中,点E,F分别在AC,BC上,且AE AC=AP AF,则下列不正确的是( )
A.△AEP∽△AFC B.△ABF∽△BCE C.△ABP∽△PAE D.△PBF∽△CBE
7.如图,在正方形ABCD中,E为CD的中点,P为BC边上一点,在下列条件中:
①∠APB=∠EPC;②AB PC=EC BP;③P为BC的中点;④PB:BC=2:3.其中能得到△ABP与△ECP相似的是( )
A.①②③④ B.①③④ C.①②④ D.②③
8.如图,CD是Rt△ABC斜边AB上的中线,过点C作CE⊥CD交AB的延长线于点E,添加下列条件仍不能判断△CEB与△CAD相似的是( )
A.∠CBA=2∠A B.点B是DE的中点
C.CE CD=CA CB D.=
9.如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )
A.②④ B.②⑤ C.③④ D.④⑤
10.如图,在矩形ABCD中,点E,F分别在BC,CD边上,EF⊥AE,BH⊥AC于点H,EF与AC交于点M,BH与AE交于点N.则下列结论错误的是( )
A.△EFC∽△AEB B.△ECM∽△ABN C.△CFM∽△BEN D.△ANH∽△EFC
二.填空题(共10小题,满分30分)
11.如图,在△ABC中,AB=8,BC=16,点P是AB边的中点,点Q是BC边上一个动点,当BQ= 时,△BPQ与△BAC相似.
12.如图,在Rt△ABC的直角边AC上有一任意点P(不与点A、C重合),过点P作一条直线,将△ABC分成一个三角形和一个四边形,则所得到的三角形与原三角形相似的直线最多有 条.
13.如图,在平面直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,过点C的直线l将△AOB截成两部分,直线l交折线A﹣O﹣B于点P.当截成两部分中有三角形与△AOB相似时,点P的坐标为 .
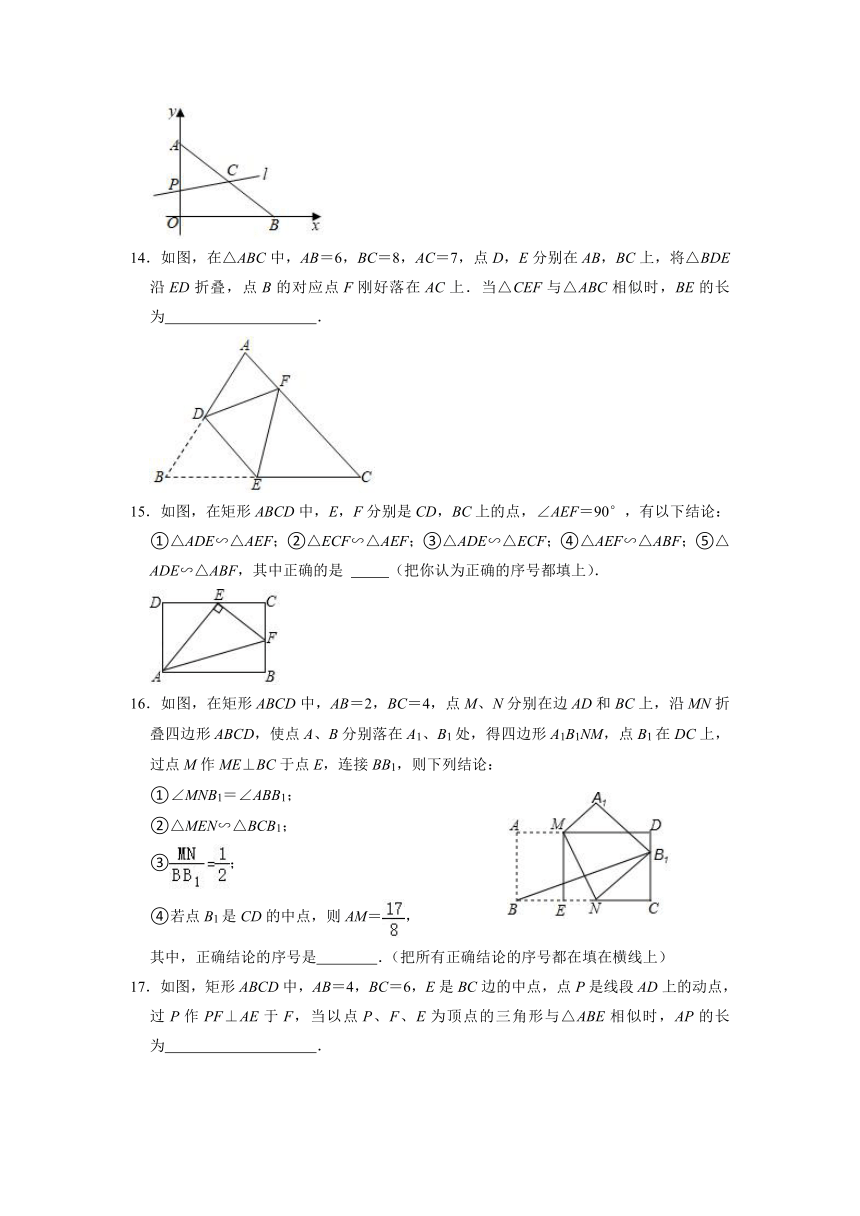
14.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
15.如图,在矩形ABCD中,E,F分别是CD,BC上的点,∠AEF=90°,有以下结论:①△ADE∽△AEF;②△ECF∽△AEF;③△ADE∽△ECF;④△AEF∽△ABF;⑤△ADE∽△ABF,其中正确的是 (把你认为正确的序号都填上).
16.如图,在矩形ABCD中,AB=2,BC=4,点M、N分别在边AD和BC上,沿MN折叠四边形ABCD,使点A、B分别落在A1、B1处,得四边形A1B1NM,点B1在DC上,过点M作ME⊥BC于点E,连接BB1,则下列结论:
①∠MNB1=∠ABB1;
②△MEN∽△BCB1;
③;
④若点B1是CD的中点,则AM=,
其中,正确结论的序号是 .(把所有正确结论的序号都在填在横线上)
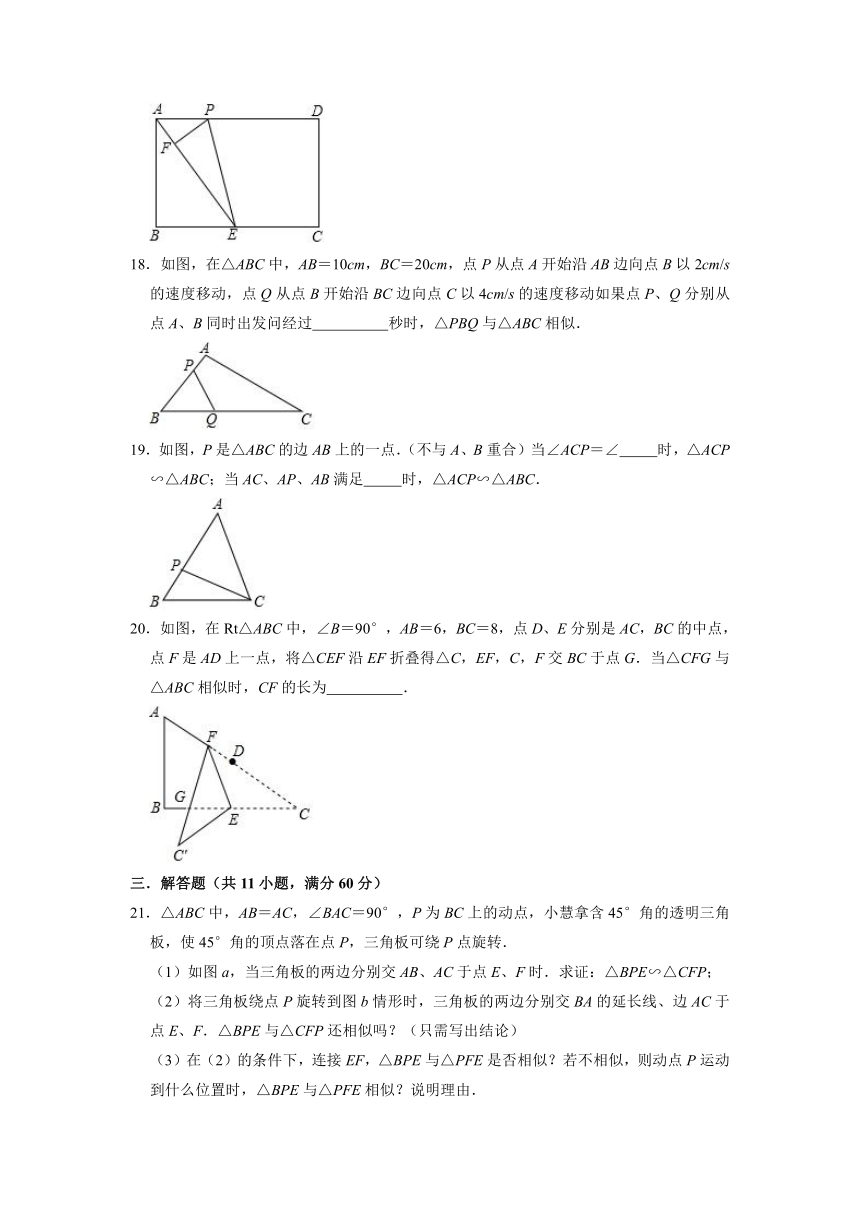
17.如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P是线段AD上的动点,过P作PF⊥AE于F,当以点P、F、E为顶点的三角形与△ABE相似时,AP的长为 .
18.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动如果点P、Q分别从点A、B同时出发问经过 秒时,△PBQ与△ABC相似.
19.如图,P是△ABC的边AB上的一点.(不与A、B重合)当∠ACP=∠ 时,△ACP∽△ABC;当AC、AP、AB满足 时,△ACP∽△ABC.
20.如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,点D、E分别是AC,BC的中点,点F是AD上一点,将△CEF沿EF折叠得△C,EF,C,F交BC于点G.当△CFG与△ABC相似时,CF的长为 .
三.解答题(共11小题,满分60分)
21.△ABC中,AB=AC,∠BAC=90°,P为BC上的动点,小慧拿含45°角的透明三角板,使45°角的顶点落在点P,三角板可绕P点旋转.
(1)如图a,当三角板的两边分别交AB、AC于点E、F时.求证:△BPE∽△CFP;
(2)将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F.△BPE与△CFP还相似吗?(只需写出结论)
(3)在(2)的条件下,连接EF,△BPE与△PFE是否相似?若不相似,则动点P运动到什么位置时,△BPE与△PFE相似?说明理由.
22.如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连接PQ.设动点运动时间为x秒.
(1)含x的代数式表示BQ、PB的长度;
(2)x为何值时,△PBQ为等腰三角形?当△BPQ和△BAC相似时,求此时x的值.
23.如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F,
(Ⅰ)证明:△ABD≌△BCE;
(Ⅱ)证明:△ABE∽△FAE;
(Ⅲ)若AF=7,DF=1,求BD的长.
24.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;
(2)求证:△AFD∽△CFE.
25.△ABC中,∠ACB=90°,CB=6,AC=8,点D是AC上的一点,点E是BD上一点.
(1)如图(1),若点D在AB的垂直平分线上,求CD的长.
(2)如图(2),连接AE,若AE平分∠BAC,BE平分∠ABC,求点E到AC的距离.
(3)若点E到三角形两边的距离均为1.5,求CD的长.(直接写出答案).
26.如图1,点E是正方形ABCD对角线AC上的一点,连接EB、ED.
(1)求证:EB=ED.
(2)如图2,延长BE交CD于F,点G在AB上,连接FG交DE于点O,如果FB=FG,请求证:△FDO∽△FBC.
27.如图,Rt△ABC中,∠ACB=90°,BC=2AC,点E是AC边中点,过点A作AD⊥AB,交BE的延长线于点D,作CH⊥AB交BE于点G,F是AB边上一动点,连接CF.
(1)若∠ACF=∠BCG.①求证:AD=CG;②求
(2)设AC=2,若以B、F、C为顶点的三角形与△ADE相似,求BF的长.
28.如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗?为什么?
29.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
30.如图,在△ABC中,AD⊥BC,垂足为D,EC⊥AB,垂足为E,连接DE.试说明△BDE∽△BAC.
31.已知线段AC上有一动点B,分别以AB、BC为边向线段的同一侧作等边三角形△ABD和△BCE.连接AE、CD(如图),若MN分别为AE、CD的中点,
(1)求证:AM=CN;
(2)求∠MBN的大小;
(3)若连接MN,请你尽可能多的说出图中相似三角形和全等三角形.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵点C在第一象限,
∴当点C为直角顶点时,有两种情形,
当点A为直角顶点时,也有两种情形,共有4种情形.
故选:D.
2.解:在△ADC和△BAC中,∠ADC=∠BAC,
如果△ADC∽△BAC,需满足的条件有:
①∠DAC=∠ABC或AC是∠BCD的平分线;
②=;
故选:C.
3.解:∵BD⊥AC,CE⊥AB,
∴∠AEC=∠ADB=90°,∠BEF=∠CDF=90°,
∵∠A=∠A,∠EFB=∠DFC,
∴△AEC∽△ADB,△BEF∽△CDF,
∵∠EBF=∠ABD,∠BEF=∠ADB=90°,
∴△BEF∽△BDA∽△CEA∽△CDF,
∴共有6对相似三角形,
故选:A.
4.解:①在△ABE与△ACB中,∠ABE=∠C,∠BAE=∠CAB,则△ABE∽△ACB;
②∵AD平分∠BAC,
∴∠1=∠2.
∵∠1=∠2,∠ABF=∠C,
∴△ABF∽△ACD;
③∵ABE∽△ACB,
∴∠BEA=∠ABD,
又∵∠1=∠2,
∴△AEF∽△ABD,
综合①②③知,共有3对相似三角形,
故选:C.
5.解:∵四边形ABCD是正方形,
∴AB=BC=CD,
∵AG=CE,
∴BG=BE,
∴∠BEG=45°,
∴∠BEA>45°,
∵∠AEF=90°,
∴∠HEC<45°,
则HC<EC,
∴CD﹣CH>BC﹣CE,即DH>BE,故①错误;
∵BG=BE,∠B=90°,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∴∠GAE+∠AEG=45°,
∵AE⊥EF,
∴∠AEF=90°,
∵∠BEG=45°,
∴∠AEG+∠FEC=45°,
∴∠GAE=∠FEC,
在△GAE和△CEF中,
∵
∴△GAE≌△CEF(SAS),∴②正确;
∴∠AGE=∠ECF=135°,
∴∠FCD=135°﹣90°=45°,∴③正确;
∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,
∴∠FEC<45°,
∴△GBE和△ECH不相似,∴④错误;
故选:C.
6.解:∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠C=∠BAC=60°,
∵AE AC=AP AF,
∴=,
∵∠PAE=∠CAF,
∴△PAE∽△CAF,
∴∠APE=∠C=60°,
∵∠APE=∠ABP+∠BAP=60°,∠BAP+∠CAF=60°,
∴∠CAF=∠ABE,
∴∠BAF=∠CBE,
∵∠ABF=∠C,
∴△ABF∽△BCE,
∵∠BPF=∠APE=∠C,∠PBF=∠CBE,
∴△PBF∽△CBE,
故选项A,B,D正确,
故选:C.
7.解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∵∠APB=∠EPC,
∴△ABP和△ECP相似,故①正确;
∵AB PC=EC BP,
∴=,
∵∠B=∠C,
∴△ABP∽△ECP,故②正确,
∵P为BC的中点,E为DC的中点,
∴BP=CP=BC,CE=CD,
∵四边形ABCD是正方形,
∴AB=BC=CD,
∴BP=CP=CE,
∴==2,=1,
即≠,
即△ABP和△ECP不相似,故③错误;
设PB=2x,BC=3x,
则PC=3x﹣2x=x,AB=BC=3x,CE=BC=x,
∴==,==,
即=,
∴=,
∵∠B=∠C=90°,
即△ABP和△ECP相似,故④正确;
所以正确的为①②④,
故选:C.
8.解:∵CE⊥CD,
∴∠EDC=90°,
∵∠BCA=90°,
∴∠BCE=∠DCA=90°﹣∠BCD,
∵CD是Rt△ABC斜边AB上的中线,
∴DC=DB=DA,
∴∠DAC=∠A,
∴∠BCE=∠DCA=∠A,
∵∠CBA=2∠A,∠CBA+∠A=90°,
∴∠A=∠BCE=∠DCA=30°,∠CBA=60°,
∴∠E=∠CBA﹣∠BCE=30°,
∴∠BCE=∠DCA=∠E=∠A,
∴△CEB∽△CAD,
∴A不符合题意,
∵点B是DE的中点,
∴BE=BC,
∴∠BCE=∠E,
∴∠BCE=∠E=∠DCA=∠A,
∴△CEB∽△CAD,
∴B不符合题意,
∵CE CD=CA CB,
∴=,
∵∠BCE=∠DCA,
∴△CEB∽△CAD,
∴C不符合题意.
由=,由于∠E和∠A不能判断相等,故不能判断△CEB与△CAD相似,
∴D符合题意,
故选:D.
9.解:由题意:①②④中,∠ABC=∠ADE=∠AFH=135°,
又∵===,
∴=,=,
∴△ABC∽△ADE∽△HFA,
故选:A.
10.解:∵矩形ABCD,
∴∠ABE=∠ECF,
∵∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
∴△EFC∽△AEB,故A正确;
∵∠ANH+∠NAH=90°,∠NAH+∠AME=90°,
∴∠ANH=∠AME,
∴∠ANB=∠EMC,
∴△ABN∽△EMC,故B正确
∴∠BNE=∠FMC,
∵∠AEB=∠EFC,
∴△BNE∽△MFC,故C正确;
故选:D.
二.填空题(共10小题,满分30分)
11.解:∵AB=8,BC=16,点P是AB边的中点,
∴BP=4.
当△BPQ∽△BAC时,
则=,
故=,
解得:BQ=8;
当△BPQ∽△BCA时,
则=,
故=,
解得:BQ=2,
综上所述:当BQ=2或8时,△BPQ与△BAC相似.
故答案为:2或8.
12.解:如图所示,
①过点P作AB的垂线段PD,则△ADP∽△ACB;
②过点P作BC的平行线PE,交AB于E,则△APE∽△ACB;
③过点P作AB的平行线PF,交BC于F,则△PCF∽△ACB;
④作∠PGC=∠A,则△GCP∽△ACB.
故答案为:4.
13.解:当PC∥OB时,△APC∽△AOB,
由点C是AB的中点,可得P为OA的中点,
此时P点坐标为(0,3);
当PC∥OA时,△BCP∽△BAO,
由点C是AB的中点,可得P为OB的中点,
此时P点坐标为(4,0);
当PC⊥AB时,如图,
∵∠CBP=∠OBA,
∴Rt△BPC∽Rt△BAO,
∴=,
∵点B(8,0)和点A(0,6),
∴AB==10,
∵点C是AB的中点,
∴BC=5,
∴=,
∴BP=,
∴OP=OB﹣BP=8﹣=,
此时P点坐标为(,0),
综上所述,满足条件的P点坐标为(0,3)、(4,0)、(,0).
故答案为:(0,3)、(4,0)、(,0).
14.解:∵将△BDE沿DE翻折得到△FDE,
∴BE=EF,
∵BC=8,
∴CE=8﹣BE,
当△CEF与△ABC相似时,=或=,即=或=,
解得:BE=或,
故答案是:或.
15.解:在矩形ABCD中,
∵∠D=∠C=90°,∠AEF=90°,
∴∠DEA+∠CEF=90°,∠DEA+∠DAE=90°,
∴∠DAE=∠CEF,
∴△ADE∽△ECF,
其余都不符合相似的条件.
故答案为:③.
16.解:由折叠可知:∠MNB1=∠BNM,MN⊥BB1,
∴∠BNM+∠B1BN=90°,
∵∠ABB1+∠B1BN=90°,
∴∠BNM=∠ABB1,
∴∠MNB1=∠ABB1,故①正确;
∵ME⊥BC,
∴∠MNE+∠NME=90°,
由折叠的性质可得:MN⊥BB1,
∴∠MNE+∠B1BN=90°,
∴∠NME=∠BB1N,
∴△MEN∽△BCB1,故②正确;
由②可知:=,
∵ME=AB=2,BC=4,
∴==,为定值,故③正确;
∵△MEN∽△BCB1,
∴==,
∴NE=B1C,
若点B1是CD的中点,则B1C=DC,
∴NE=DC=×2=,
设BN=x,则NC=4﹣x,B1N=x,
在Rt△B1NC中,由勾股定理可得x2=(4﹣x)2+12,
解得:x=,
∴AM=BE=BN﹣NE=﹣=,故④不正确.
故答案为:①②③.
17.解:分两种情况:
①若△EFP∽△ABE,如图1,则∠PEF=∠EAB,
∴PE∥AB,
∴四边形ABEP为矩形,
∴PA=EB=3,
②若△PFE∽△ABE,如图2中,则∠PEF=∠AEB,
∵AD∥BC
∴∠PAF=∠AEB,
∴∠PEF=∠PAF
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点,
Rt△ABE中,AB=4,BE=3,
∴AE=5,
∴EF=AE=,
∵△PFE∽△ABE,
∴=,
∴PE=,PA=.
∴满足条件的PA的值为3或.
故答案为3或.
18.解:设经过t秒后,△PBQ与△ABC相似,则有AP=2t,BQ=4t,BP=10﹣2t,
当△PBQ∽△ABC时,有BP:AB=BQ:BC,
即(10﹣2t):10=4t:20,
解得t=2.5(s)
当△QBP∽△ABC时,有BQ:AB=BP:BC,即4t:10=(10﹣2t):20,
解得t=1.
所以,经过2.5s或1s时,△PBQ与△ABC相似.
解法二:设ts后,△PBQ与△ABC相似,则有,AP=2t,BQ=4t,BP=10﹣2t
分两种情况:
(1)当BP与AB对应时,有,即,解得t=2.5s
(2)当BP与BC对应时,有,即,解得t=1s
所以经过1s或2.5s时,以P、B、Q三点为顶点的三角形与△ABC相似,
故答案为:1或2.5
19.解:∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC;
∵,∠A=∠A,
∴△ACP∽△ABC;
故答案为:B;.
20.解:由勾股定理得:AC=10,
①当FG⊥BC时,
∵将△CEF沿EF折叠得△C′EF,
∴∠C′=∠C,C′E=CE=4,
∴sin∠C=sin∠C′,
∴=,
∴EG=2.4,
∵FG∥AB,
∴=,即=,
∴CF=8;
②当GF⊥AC时,如图,
∵将△CEF沿EF折叠得△C′EF,
∴∠1=∠2=45°,
∴HF=HE,
∵sin∠C=sin∠C′==,
∴EH=4×=,
∴C′H==3.2,
∴CF=C′F=C′H+HF=3.2+2.4=5.6.
综上所述,当△CFG与△ABC相似时,CF的长为8或5.6.
故答案为:8或5.6.
三.解答题(共11小题,满分60分)
21.(1)证明:∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=135°,
∵∠EPF=45°,
又∵∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=135°,
∴∠BEP=∠CPF,
又∵∠B=∠C,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(2)解:△BPE∽△CFP;
理由:∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=135°,
∵∠EPF=45°,
又∵∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=135°,
∴∠BEP=∠CPF,
又∵∠B=∠C,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(3)解:动点P运动到BC中点位置时,△BPE与△PFE相似,
证明:同(1),可证△BPE∽△CFP,
得 CP:BE=PF:PE,
而CP=BP,
因此 PB:BE=PF:PE.
又因为∠EBP=∠EPF,
所以△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).
22.解:(1)∵∠B=90°,AC=10cm,BC=6cm,
∴AB===8(cm).
由运动可知:BQ=x(cm),PA=2x(cm),
∴PB=(8﹣2x)cm.
(2)由题意,得
8﹣2x=x,
∴x=.
∴当x=时,△PBQ为等腰三角形.
当BP:BA=BQ:BC时,两三角形相似,此时(8﹣2x):8=x:6,解得x=,
当BP:BC=BQ:AB时,两三角形相似,此时(8﹣2x):6=x:8,解得x=,
综上所述,满足条件的x的值为或.
23.解:(Ⅰ)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE,
在△ABD与△BCE中
,
∴△ABD≌△BCE(SAS);
(Ⅱ)由(1)得:∠BAD=∠CBE,
又∵∠ABC=∠BAC,
∴∠ABE=∠EAF,
又∵∠AEF=∠BEA,
∴△AEF∽△BEA;
(Ⅲ)∵∠BAD=∠CBE,∠BDA=∠FDB,
∴△ABD∽△BFD,
∴,
∴BD2=AD DF=(AF+DF) DF=8,
∴BD=2.
24.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB AD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE.
25.解:∠ACB=90°,CB=6,AC=8,
∴AB==10.
(1)如图1所示,
∵点D在AB的垂直平分线上,
设AB的垂直平分线为DF,垂足为F,
∴AD=BD,AF=BF=AB=5,
设CD=x,则AD=BD=8﹣x,
在Rt△BCD中,根据勾股定理,得
62+x2=(8﹣x)2,
解得x=,
∴点D在AB的垂直平分线上时,CD的长为;
(2)如图2所示,过点E作EF⊥AC于点F,EM⊥AB于点M,EN⊥BC于点N,连接CE,
∵AE平分∠BAC,EF⊥AC,EM⊥AB,
∴EF=EM,
∵BE平分∠ABC,EN⊥BC,EM⊥AB,
∴EN=EM,
∴EF=EM=EN,
设EF=EM=EN=x,则:
S△ABC=S△AEC+S△AEB+S△BEC,
即AC BC=AC EF+AB EM+BC EN,
∴6×8=8x+10x+6x,
解得x=2,
∴点E到AC的距离为2;
(3)根据题意可分三种情况:
①如图3所示,当点E到AB和BC的距离为1.5时,此时点E在∠CBA的角平分线上,
即BD平分∠ABC,过点D作DF⊥AB于点F,
则CD=DF,
∵∠C=∠BFD=90°,BD=BD,
∴Rt△BCD≌Rt△BFD(HL),
∴BF=BC=6,
∴AF=4,
设CD=x,则DF=x,AD=8﹣x,
在Rt△AFD中,根据勾股定理,得
42+x2=(8﹣x)2,
解得x=3,
∴当点E到AB和BC的距离为1.5时,CD=3;
②方法一:
如图4所示,当点E到AC和BC的距离为1.5时,此时点E在∠BCA的角平分线上,
即CE平分∠BCA,过点E作EM⊥AC于点M,EN⊥BC于点N,
此时EM=EN=1.5,EM∥BC,
∵∠NCM=90°,EM⊥AC,EN⊥BC,
∴四边形ENCM是矩形,
∵EM=EN,
∴矩形ENCM是正方形,
∴CM=1.5,
设CD=x,则DM=x﹣1.5,
∵EM∥BC,
∴△DEM∽△DBC,
∴=,
即=,
解得x=2,
方法二:
∵S△BCD=S△BEC+S△CED,
∴BC CD=1.5BC+1.5CD,
即6x=9+1.5x,
解得x=2,
∴CD=2.
∴当点E到AC和BC的距离为1.5时,CD=2;
③方法一:
如图5所示,当点E到AC和AB的距离为1.5时,此时点E在∠BAC的角平分线上,
即AE平分∠BAC,过点E作EM⊥A于B点M,EN⊥AC于点N,
此时EM=EN=1.5,作EF⊥BC于点F,
得矩形EFCN,
∵S△ABC=S△AEC+S△AEB+S△BEC,
即AC BC=AC EN+AB EM+BC EF,
∴6×8=8×1.5+10×1.5+6EF,
解得EF=,
∴CN=EF=,
设CD=x,则DN=x﹣,
∵EN∥BC,
∴△DEN∽△DBC,
∴=,
即=,
解得x=,
方法二:
设CD=x,则AD=8﹣x,EM=EN=1.5,AB=10,BC=6,
∵S△BEA+S△DEA=S△BDA,
∴AB EM+AD EN=AD BC,
即10×1.5+1.5(8﹣x)=6(8﹣x),
解得x=.
∴当点E到AC和AB的距离为1.5时,CD=.
综上所述,点E到三角形两边的距离均为1.5,CD的长为3或2或.
26.证明:(1)∵四边形ABCD是正方形,
∴DC=BC,∠DCE=∠BCA=45°,
在△DCE和△BCE中
∴△DCE≌△BCE(SAS),
∴BE=ED;
(2)∵四边形ABCD是正方形,
∴DC∥AB,
∴∠DFO=∠FGB,∠CFB=∠FBG,
∵FB=FG,
∴∠FGB=∠FBG,
∴∠DFO=∠CFB,
∵△DCE≌△BCE,
∴∠CDG=∠CBF,
∴△FDO∽△FBC.
27.解:(1)①∵AD⊥AB,CH⊥AB,
∴AD∥CH,
∴∠DAC=∠ECG,
∵点E是AC边中点,
∴AE=CE,
在△ADE与△CGF中,,
∴△ADE≌△CGF,(ASA),
∴AD=CG;
②∵∠ACB=∠AHC=∠CHB=90°,
∴△ACH∽△BCH∽△ACB,
∴=,
∴BH=4AH,
∴AB=5AH,
∵HG∥AD,
∴△BHG∽△BAD,
∴=,
连接HE,
∴S△HEC=S△ACH,
∵=,
∴=,
∴CG=CH,
∴S△CGE=S△CHE,
∴S△ADE=S△CEH,
∴S△ADE=S△ACH,
∵∠ACF=∠BCG,
∴∠ACH=∠BCF,
∵∠ACH=∠ABC,
∴∠FCB=∠BCF,
∴CF=BF,
过F作FM⊥BC于M,
∴CM=BM=AC,
∴S△BCF=2S△CMF,
∵∠ACH=∠ABC=∠FCB,
∴=2°,
∴AH2+CH2=AC2,
∴AH2+4AH2=4,
∴AH=,CH=,
∴FM=CM=1,
∴S△ACH=,S△CFB=2,
∴S△ACH=S△BCF,
∴=;
(2)∵AC=2,
∴BC=4,AE=1,
∴AB==2,
∵S△ABC=AC BC=AB CH,
∴CH==,
∴AH=,
∵AD⊥AB,CH⊥AB,
∴AD∥HG,
∴=,∠DAE=∠GCE,
∵∠AED=∠CEG,AE=CE,
∴△ADE≌△CGE(ASA),
∴AD=CG,
∴=,
∴CG=,
∴AD=CG=,
∵∠DAE=∠ACH=∠BCF,
∴以B、F、C为顶点的三角形与△ADE相似,
∴或,
∴=或=,
∴BF=或.
28.解:(1)∵DE是BC垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
∵AB=AD,
∴∠ABC=∠ADB,
∴△FDB∽△ABC;
(2)∵△FDB∽△ABC,
∴==,
∴AB=2FD,
∵AB=AD,
∴AD=2FD,
∴DF=AF.
29.解:(1)∵∠ACB=90°,AC=3,BC=4,
∴AB==5.
∵AD=5t,CE=3t,
∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1.
(2)∵EF=BC=4,G是EF的中点,
∴GE=2.
当AD<AE(即t<)时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则 或 ,
∴或 ,
∴t=或t=;
当AD>AE(即t>)时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则 或 ,
∴或 ,
解得t=或t=;
综上所述,当t=或 或 或 时,△DEG与△ACB相似.
30.证明:∵AD⊥BC
∴∠ADB=90°
∵EC⊥AB
∴∠CEB=90°
∴点D和点E在以AC为直径的圆上,
∴∠BDE=∠BAC,
而∠DBE=∠ABC,
∴△BDE∽△BAC.
31.(1)证明:∵△ABD和△BCE是等边三角形,
∴AB=BD,BC=BE,∠EBC=∠ABC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中
∴△ABE≌△DBC(SAS)
∴AE=DC,
∵M、N分别为AE、CD的中点,
∴AM=AE,CN=DC
∴AM=CN;
(2)解:∵△ABE≌△DBC,
∴∠EAB=∠CDB,
在△AMB和△DNB中
∴△AMB≌△DNB(SAS),
∴∠ABM=∠DBN,
∵∠ABC=∠ABM+∠MBD=60°,
∴∠DBN+∠MBD=60°,
即∠MBN=60°;
(3)解:图中的全等三角形有:△ABM≌△DBN,△BME≌△BCN,△ABE≌△DBC;
相似三角形有:△ABD∽△BCE,△ABD∽△BMN,△BMN∽△BCE.
一.选择题(共10小题,满分30分)
1.如图所示,直线y=x﹣1与x轴交于A,与y轴交于B,在第一象限内找点C,使△AOC与△AOB相似,则共能找到的点C的个数( )
A.1 B.2 C.3 D.4
2.如图,在四边形ABCD中,已知∠ADC=∠BAC,那么补充下列条件后不能判定△ADC和△BAC相似的是( )
A.CA平分∠BCD B. C.AC2=BC CD D.∠DAC=∠ABC
3.如图,△ABC中,CE⊥AB,垂足为E,BD⊥AC,垂足为点D,CE与BD交于点F,则图中相似三角形有几对( )
A.6对 B.5对 C.4对 D.3对
4.如图,△ABC中,D、E两点分别在BC、AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F.则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
5.如图,G,E分别是正方形ABCD的边AB,BC上的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=DH;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH.其中,正确的结论有( )
A.4个 B.3个 C.2个 D.1个
6.如图,在等边三角形ABC中,点E,F分别在AC,BC上,且AE AC=AP AF,则下列不正确的是( )
A.△AEP∽△AFC B.△ABF∽△BCE C.△ABP∽△PAE D.△PBF∽△CBE
7.如图,在正方形ABCD中,E为CD的中点,P为BC边上一点,在下列条件中:
①∠APB=∠EPC;②AB PC=EC BP;③P为BC的中点;④PB:BC=2:3.其中能得到△ABP与△ECP相似的是( )
A.①②③④ B.①③④ C.①②④ D.②③
8.如图,CD是Rt△ABC斜边AB上的中线,过点C作CE⊥CD交AB的延长线于点E,添加下列条件仍不能判断△CEB与△CAD相似的是( )
A.∠CBA=2∠A B.点B是DE的中点
C.CE CD=CA CB D.=
9.如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )
A.②④ B.②⑤ C.③④ D.④⑤
10.如图,在矩形ABCD中,点E,F分别在BC,CD边上,EF⊥AE,BH⊥AC于点H,EF与AC交于点M,BH与AE交于点N.则下列结论错误的是( )
A.△EFC∽△AEB B.△ECM∽△ABN C.△CFM∽△BEN D.△ANH∽△EFC
二.填空题(共10小题,满分30分)
11.如图,在△ABC中,AB=8,BC=16,点P是AB边的中点,点Q是BC边上一个动点,当BQ= 时,△BPQ与△BAC相似.
12.如图,在Rt△ABC的直角边AC上有一任意点P(不与点A、C重合),过点P作一条直线,将△ABC分成一个三角形和一个四边形,则所得到的三角形与原三角形相似的直线最多有 条.
13.如图,在平面直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,过点C的直线l将△AOB截成两部分,直线l交折线A﹣O﹣B于点P.当截成两部分中有三角形与△AOB相似时,点P的坐标为 .
14.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
15.如图,在矩形ABCD中,E,F分别是CD,BC上的点,∠AEF=90°,有以下结论:①△ADE∽△AEF;②△ECF∽△AEF;③△ADE∽△ECF;④△AEF∽△ABF;⑤△ADE∽△ABF,其中正确的是 (把你认为正确的序号都填上).
16.如图,在矩形ABCD中,AB=2,BC=4,点M、N分别在边AD和BC上,沿MN折叠四边形ABCD,使点A、B分别落在A1、B1处,得四边形A1B1NM,点B1在DC上,过点M作ME⊥BC于点E,连接BB1,则下列结论:
①∠MNB1=∠ABB1;
②△MEN∽△BCB1;
③;
④若点B1是CD的中点,则AM=,
其中,正确结论的序号是 .(把所有正确结论的序号都在填在横线上)
17.如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P是线段AD上的动点,过P作PF⊥AE于F,当以点P、F、E为顶点的三角形与△ABE相似时,AP的长为 .
18.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动如果点P、Q分别从点A、B同时出发问经过 秒时,△PBQ与△ABC相似.
19.如图,P是△ABC的边AB上的一点.(不与A、B重合)当∠ACP=∠ 时,△ACP∽△ABC;当AC、AP、AB满足 时,△ACP∽△ABC.
20.如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,点D、E分别是AC,BC的中点,点F是AD上一点,将△CEF沿EF折叠得△C,EF,C,F交BC于点G.当△CFG与△ABC相似时,CF的长为 .
三.解答题(共11小题,满分60分)
21.△ABC中,AB=AC,∠BAC=90°,P为BC上的动点,小慧拿含45°角的透明三角板,使45°角的顶点落在点P,三角板可绕P点旋转.
(1)如图a,当三角板的两边分别交AB、AC于点E、F时.求证:△BPE∽△CFP;
(2)将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F.△BPE与△CFP还相似吗?(只需写出结论)
(3)在(2)的条件下,连接EF,△BPE与△PFE是否相似?若不相似,则动点P运动到什么位置时,△BPE与△PFE相似?说明理由.
22.如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连接PQ.设动点运动时间为x秒.
(1)含x的代数式表示BQ、PB的长度;
(2)x为何值时,△PBQ为等腰三角形?当△BPQ和△BAC相似时,求此时x的值.
23.如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F,
(Ⅰ)证明:△ABD≌△BCE;
(Ⅱ)证明:△ABE∽△FAE;
(Ⅲ)若AF=7,DF=1,求BD的长.
24.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;
(2)求证:△AFD∽△CFE.
25.△ABC中,∠ACB=90°,CB=6,AC=8,点D是AC上的一点,点E是BD上一点.
(1)如图(1),若点D在AB的垂直平分线上,求CD的长.
(2)如图(2),连接AE,若AE平分∠BAC,BE平分∠ABC,求点E到AC的距离.
(3)若点E到三角形两边的距离均为1.5,求CD的长.(直接写出答案).
26.如图1,点E是正方形ABCD对角线AC上的一点,连接EB、ED.
(1)求证:EB=ED.
(2)如图2,延长BE交CD于F,点G在AB上,连接FG交DE于点O,如果FB=FG,请求证:△FDO∽△FBC.
27.如图,Rt△ABC中,∠ACB=90°,BC=2AC,点E是AC边中点,过点A作AD⊥AB,交BE的延长线于点D,作CH⊥AB交BE于点G,F是AB边上一动点,连接CF.
(1)若∠ACF=∠BCG.①求证:AD=CG;②求
(2)设AC=2,若以B、F、C为顶点的三角形与△ADE相似,求BF的长.
28.如图,在△ABC中,BC的垂直平分线分别交BC,AC于点D,E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由.
(2)AF与DF相等吗?为什么?
29.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
30.如图,在△ABC中,AD⊥BC,垂足为D,EC⊥AB,垂足为E,连接DE.试说明△BDE∽△BAC.
31.已知线段AC上有一动点B,分别以AB、BC为边向线段的同一侧作等边三角形△ABD和△BCE.连接AE、CD(如图),若MN分别为AE、CD的中点,
(1)求证:AM=CN;
(2)求∠MBN的大小;
(3)若连接MN,请你尽可能多的说出图中相似三角形和全等三角形.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵点C在第一象限,
∴当点C为直角顶点时,有两种情形,
当点A为直角顶点时,也有两种情形,共有4种情形.
故选:D.
2.解:在△ADC和△BAC中,∠ADC=∠BAC,
如果△ADC∽△BAC,需满足的条件有:
①∠DAC=∠ABC或AC是∠BCD的平分线;
②=;
故选:C.
3.解:∵BD⊥AC,CE⊥AB,
∴∠AEC=∠ADB=90°,∠BEF=∠CDF=90°,
∵∠A=∠A,∠EFB=∠DFC,
∴△AEC∽△ADB,△BEF∽△CDF,
∵∠EBF=∠ABD,∠BEF=∠ADB=90°,
∴△BEF∽△BDA∽△CEA∽△CDF,
∴共有6对相似三角形,
故选:A.
4.解:①在△ABE与△ACB中,∠ABE=∠C,∠BAE=∠CAB,则△ABE∽△ACB;
②∵AD平分∠BAC,
∴∠1=∠2.
∵∠1=∠2,∠ABF=∠C,
∴△ABF∽△ACD;
③∵ABE∽△ACB,
∴∠BEA=∠ABD,
又∵∠1=∠2,
∴△AEF∽△ABD,
综合①②③知,共有3对相似三角形,
故选:C.
5.解:∵四边形ABCD是正方形,
∴AB=BC=CD,
∵AG=CE,
∴BG=BE,
∴∠BEG=45°,
∴∠BEA>45°,
∵∠AEF=90°,
∴∠HEC<45°,
则HC<EC,
∴CD﹣CH>BC﹣CE,即DH>BE,故①错误;
∵BG=BE,∠B=90°,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∴∠GAE+∠AEG=45°,
∵AE⊥EF,
∴∠AEF=90°,
∵∠BEG=45°,
∴∠AEG+∠FEC=45°,
∴∠GAE=∠FEC,
在△GAE和△CEF中,
∵
∴△GAE≌△CEF(SAS),∴②正确;
∴∠AGE=∠ECF=135°,
∴∠FCD=135°﹣90°=45°,∴③正确;
∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,
∴∠FEC<45°,
∴△GBE和△ECH不相似,∴④错误;
故选:C.
6.解:∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠C=∠BAC=60°,
∵AE AC=AP AF,
∴=,
∵∠PAE=∠CAF,
∴△PAE∽△CAF,
∴∠APE=∠C=60°,
∵∠APE=∠ABP+∠BAP=60°,∠BAP+∠CAF=60°,
∴∠CAF=∠ABE,
∴∠BAF=∠CBE,
∵∠ABF=∠C,
∴△ABF∽△BCE,
∵∠BPF=∠APE=∠C,∠PBF=∠CBE,
∴△PBF∽△CBE,
故选项A,B,D正确,
故选:C.
7.解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∵∠APB=∠EPC,
∴△ABP和△ECP相似,故①正确;
∵AB PC=EC BP,
∴=,
∵∠B=∠C,
∴△ABP∽△ECP,故②正确,
∵P为BC的中点,E为DC的中点,
∴BP=CP=BC,CE=CD,
∵四边形ABCD是正方形,
∴AB=BC=CD,
∴BP=CP=CE,
∴==2,=1,
即≠,
即△ABP和△ECP不相似,故③错误;
设PB=2x,BC=3x,
则PC=3x﹣2x=x,AB=BC=3x,CE=BC=x,
∴==,==,
即=,
∴=,
∵∠B=∠C=90°,
即△ABP和△ECP相似,故④正确;
所以正确的为①②④,
故选:C.
8.解:∵CE⊥CD,
∴∠EDC=90°,
∵∠BCA=90°,
∴∠BCE=∠DCA=90°﹣∠BCD,
∵CD是Rt△ABC斜边AB上的中线,
∴DC=DB=DA,
∴∠DAC=∠A,
∴∠BCE=∠DCA=∠A,
∵∠CBA=2∠A,∠CBA+∠A=90°,
∴∠A=∠BCE=∠DCA=30°,∠CBA=60°,
∴∠E=∠CBA﹣∠BCE=30°,
∴∠BCE=∠DCA=∠E=∠A,
∴△CEB∽△CAD,
∴A不符合题意,
∵点B是DE的中点,
∴BE=BC,
∴∠BCE=∠E,
∴∠BCE=∠E=∠DCA=∠A,
∴△CEB∽△CAD,
∴B不符合题意,
∵CE CD=CA CB,
∴=,
∵∠BCE=∠DCA,
∴△CEB∽△CAD,
∴C不符合题意.
由=,由于∠E和∠A不能判断相等,故不能判断△CEB与△CAD相似,
∴D符合题意,
故选:D.
9.解:由题意:①②④中,∠ABC=∠ADE=∠AFH=135°,
又∵===,
∴=,=,
∴△ABC∽△ADE∽△HFA,
故选:A.
10.解:∵矩形ABCD,
∴∠ABE=∠ECF,
∵∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
∴△EFC∽△AEB,故A正确;
∵∠ANH+∠NAH=90°,∠NAH+∠AME=90°,
∴∠ANH=∠AME,
∴∠ANB=∠EMC,
∴△ABN∽△EMC,故B正确
∴∠BNE=∠FMC,
∵∠AEB=∠EFC,
∴△BNE∽△MFC,故C正确;
故选:D.
二.填空题(共10小题,满分30分)
11.解:∵AB=8,BC=16,点P是AB边的中点,
∴BP=4.
当△BPQ∽△BAC时,
则=,
故=,
解得:BQ=8;
当△BPQ∽△BCA时,
则=,
故=,
解得:BQ=2,
综上所述:当BQ=2或8时,△BPQ与△BAC相似.
故答案为:2或8.
12.解:如图所示,
①过点P作AB的垂线段PD,则△ADP∽△ACB;
②过点P作BC的平行线PE,交AB于E,则△APE∽△ACB;
③过点P作AB的平行线PF,交BC于F,则△PCF∽△ACB;
④作∠PGC=∠A,则△GCP∽△ACB.
故答案为:4.
13.解:当PC∥OB时,△APC∽△AOB,
由点C是AB的中点,可得P为OA的中点,
此时P点坐标为(0,3);
当PC∥OA时,△BCP∽△BAO,
由点C是AB的中点,可得P为OB的中点,
此时P点坐标为(4,0);
当PC⊥AB时,如图,
∵∠CBP=∠OBA,
∴Rt△BPC∽Rt△BAO,
∴=,
∵点B(8,0)和点A(0,6),
∴AB==10,
∵点C是AB的中点,
∴BC=5,
∴=,
∴BP=,
∴OP=OB﹣BP=8﹣=,
此时P点坐标为(,0),
综上所述,满足条件的P点坐标为(0,3)、(4,0)、(,0).
故答案为:(0,3)、(4,0)、(,0).
14.解:∵将△BDE沿DE翻折得到△FDE,
∴BE=EF,
∵BC=8,
∴CE=8﹣BE,
当△CEF与△ABC相似时,=或=,即=或=,
解得:BE=或,
故答案是:或.
15.解:在矩形ABCD中,
∵∠D=∠C=90°,∠AEF=90°,
∴∠DEA+∠CEF=90°,∠DEA+∠DAE=90°,
∴∠DAE=∠CEF,
∴△ADE∽△ECF,
其余都不符合相似的条件.
故答案为:③.
16.解:由折叠可知:∠MNB1=∠BNM,MN⊥BB1,
∴∠BNM+∠B1BN=90°,
∵∠ABB1+∠B1BN=90°,
∴∠BNM=∠ABB1,
∴∠MNB1=∠ABB1,故①正确;
∵ME⊥BC,
∴∠MNE+∠NME=90°,
由折叠的性质可得:MN⊥BB1,
∴∠MNE+∠B1BN=90°,
∴∠NME=∠BB1N,
∴△MEN∽△BCB1,故②正确;
由②可知:=,
∵ME=AB=2,BC=4,
∴==,为定值,故③正确;
∵△MEN∽△BCB1,
∴==,
∴NE=B1C,
若点B1是CD的中点,则B1C=DC,
∴NE=DC=×2=,
设BN=x,则NC=4﹣x,B1N=x,
在Rt△B1NC中,由勾股定理可得x2=(4﹣x)2+12,
解得:x=,
∴AM=BE=BN﹣NE=﹣=,故④不正确.
故答案为:①②③.
17.解:分两种情况:
①若△EFP∽△ABE,如图1,则∠PEF=∠EAB,
∴PE∥AB,
∴四边形ABEP为矩形,
∴PA=EB=3,
②若△PFE∽△ABE,如图2中,则∠PEF=∠AEB,
∵AD∥BC
∴∠PAF=∠AEB,
∴∠PEF=∠PAF
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点,
Rt△ABE中,AB=4,BE=3,
∴AE=5,
∴EF=AE=,
∵△PFE∽△ABE,
∴=,
∴PE=,PA=.
∴满足条件的PA的值为3或.
故答案为3或.
18.解:设经过t秒后,△PBQ与△ABC相似,则有AP=2t,BQ=4t,BP=10﹣2t,
当△PBQ∽△ABC时,有BP:AB=BQ:BC,
即(10﹣2t):10=4t:20,
解得t=2.5(s)
当△QBP∽△ABC时,有BQ:AB=BP:BC,即4t:10=(10﹣2t):20,
解得t=1.
所以,经过2.5s或1s时,△PBQ与△ABC相似.
解法二:设ts后,△PBQ与△ABC相似,则有,AP=2t,BQ=4t,BP=10﹣2t
分两种情况:
(1)当BP与AB对应时,有,即,解得t=2.5s
(2)当BP与BC对应时,有,即,解得t=1s
所以经过1s或2.5s时,以P、B、Q三点为顶点的三角形与△ABC相似,
故答案为:1或2.5
19.解:∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC;
∵,∠A=∠A,
∴△ACP∽△ABC;
故答案为:B;.
20.解:由勾股定理得:AC=10,
①当FG⊥BC时,
∵将△CEF沿EF折叠得△C′EF,
∴∠C′=∠C,C′E=CE=4,
∴sin∠C=sin∠C′,
∴=,
∴EG=2.4,
∵FG∥AB,
∴=,即=,
∴CF=8;
②当GF⊥AC时,如图,
∵将△CEF沿EF折叠得△C′EF,
∴∠1=∠2=45°,
∴HF=HE,
∵sin∠C=sin∠C′==,
∴EH=4×=,
∴C′H==3.2,
∴CF=C′F=C′H+HF=3.2+2.4=5.6.
综上所述,当△CFG与△ABC相似时,CF的长为8或5.6.
故答案为:8或5.6.
三.解答题(共11小题,满分60分)
21.(1)证明:∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=135°,
∵∠EPF=45°,
又∵∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=135°,
∴∠BEP=∠CPF,
又∵∠B=∠C,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(2)解:△BPE∽△CFP;
理由:∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=135°,
∵∠EPF=45°,
又∵∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=135°,
∴∠BEP=∠CPF,
又∵∠B=∠C,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(3)解:动点P运动到BC中点位置时,△BPE与△PFE相似,
证明:同(1),可证△BPE∽△CFP,
得 CP:BE=PF:PE,
而CP=BP,
因此 PB:BE=PF:PE.
又因为∠EBP=∠EPF,
所以△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).
22.解:(1)∵∠B=90°,AC=10cm,BC=6cm,
∴AB===8(cm).
由运动可知:BQ=x(cm),PA=2x(cm),
∴PB=(8﹣2x)cm.
(2)由题意,得
8﹣2x=x,
∴x=.
∴当x=时,△PBQ为等腰三角形.
当BP:BA=BQ:BC时,两三角形相似,此时(8﹣2x):8=x:6,解得x=,
当BP:BC=BQ:AB时,两三角形相似,此时(8﹣2x):6=x:8,解得x=,
综上所述,满足条件的x的值为或.
23.解:(Ⅰ)∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE,
在△ABD与△BCE中
,
∴△ABD≌△BCE(SAS);
(Ⅱ)由(1)得:∠BAD=∠CBE,
又∵∠ABC=∠BAC,
∴∠ABE=∠EAF,
又∵∠AEF=∠BEA,
∴△AEF∽△BEA;
(Ⅲ)∵∠BAD=∠CBE,∠BDA=∠FDB,
∴△ABD∽△BFD,
∴,
∴BD2=AD DF=(AF+DF) DF=8,
∴BD=2.
24.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB AD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE.
25.解:∠ACB=90°,CB=6,AC=8,
∴AB==10.
(1)如图1所示,
∵点D在AB的垂直平分线上,
设AB的垂直平分线为DF,垂足为F,
∴AD=BD,AF=BF=AB=5,
设CD=x,则AD=BD=8﹣x,
在Rt△BCD中,根据勾股定理,得
62+x2=(8﹣x)2,
解得x=,
∴点D在AB的垂直平分线上时,CD的长为;
(2)如图2所示,过点E作EF⊥AC于点F,EM⊥AB于点M,EN⊥BC于点N,连接CE,
∵AE平分∠BAC,EF⊥AC,EM⊥AB,
∴EF=EM,
∵BE平分∠ABC,EN⊥BC,EM⊥AB,
∴EN=EM,
∴EF=EM=EN,
设EF=EM=EN=x,则:
S△ABC=S△AEC+S△AEB+S△BEC,
即AC BC=AC EF+AB EM+BC EN,
∴6×8=8x+10x+6x,
解得x=2,
∴点E到AC的距离为2;
(3)根据题意可分三种情况:
①如图3所示,当点E到AB和BC的距离为1.5时,此时点E在∠CBA的角平分线上,
即BD平分∠ABC,过点D作DF⊥AB于点F,
则CD=DF,
∵∠C=∠BFD=90°,BD=BD,
∴Rt△BCD≌Rt△BFD(HL),
∴BF=BC=6,
∴AF=4,
设CD=x,则DF=x,AD=8﹣x,
在Rt△AFD中,根据勾股定理,得
42+x2=(8﹣x)2,
解得x=3,
∴当点E到AB和BC的距离为1.5时,CD=3;
②方法一:
如图4所示,当点E到AC和BC的距离为1.5时,此时点E在∠BCA的角平分线上,
即CE平分∠BCA,过点E作EM⊥AC于点M,EN⊥BC于点N,
此时EM=EN=1.5,EM∥BC,
∵∠NCM=90°,EM⊥AC,EN⊥BC,
∴四边形ENCM是矩形,
∵EM=EN,
∴矩形ENCM是正方形,
∴CM=1.5,
设CD=x,则DM=x﹣1.5,
∵EM∥BC,
∴△DEM∽△DBC,
∴=,
即=,
解得x=2,
方法二:
∵S△BCD=S△BEC+S△CED,
∴BC CD=1.5BC+1.5CD,
即6x=9+1.5x,
解得x=2,
∴CD=2.
∴当点E到AC和BC的距离为1.5时,CD=2;
③方法一:
如图5所示,当点E到AC和AB的距离为1.5时,此时点E在∠BAC的角平分线上,
即AE平分∠BAC,过点E作EM⊥A于B点M,EN⊥AC于点N,
此时EM=EN=1.5,作EF⊥BC于点F,
得矩形EFCN,
∵S△ABC=S△AEC+S△AEB+S△BEC,
即AC BC=AC EN+AB EM+BC EF,
∴6×8=8×1.5+10×1.5+6EF,
解得EF=,
∴CN=EF=,
设CD=x,则DN=x﹣,
∵EN∥BC,
∴△DEN∽△DBC,
∴=,
即=,
解得x=,
方法二:
设CD=x,则AD=8﹣x,EM=EN=1.5,AB=10,BC=6,
∵S△BEA+S△DEA=S△BDA,
∴AB EM+AD EN=AD BC,
即10×1.5+1.5(8﹣x)=6(8﹣x),
解得x=.
∴当点E到AC和AB的距离为1.5时,CD=.
综上所述,点E到三角形两边的距离均为1.5,CD的长为3或2或.
26.证明:(1)∵四边形ABCD是正方形,
∴DC=BC,∠DCE=∠BCA=45°,
在△DCE和△BCE中
∴△DCE≌△BCE(SAS),
∴BE=ED;
(2)∵四边形ABCD是正方形,
∴DC∥AB,
∴∠DFO=∠FGB,∠CFB=∠FBG,
∵FB=FG,
∴∠FGB=∠FBG,
∴∠DFO=∠CFB,
∵△DCE≌△BCE,
∴∠CDG=∠CBF,
∴△FDO∽△FBC.
27.解:(1)①∵AD⊥AB,CH⊥AB,
∴AD∥CH,
∴∠DAC=∠ECG,
∵点E是AC边中点,
∴AE=CE,
在△ADE与△CGF中,,
∴△ADE≌△CGF,(ASA),
∴AD=CG;
②∵∠ACB=∠AHC=∠CHB=90°,
∴△ACH∽△BCH∽△ACB,
∴=,
∴BH=4AH,
∴AB=5AH,
∵HG∥AD,
∴△BHG∽△BAD,
∴=,
连接HE,
∴S△HEC=S△ACH,
∵=,
∴=,
∴CG=CH,
∴S△CGE=S△CHE,
∴S△ADE=S△CEH,
∴S△ADE=S△ACH,
∵∠ACF=∠BCG,
∴∠ACH=∠BCF,
∵∠ACH=∠ABC,
∴∠FCB=∠BCF,
∴CF=BF,
过F作FM⊥BC于M,
∴CM=BM=AC,
∴S△BCF=2S△CMF,
∵∠ACH=∠ABC=∠FCB,
∴=2°,
∴AH2+CH2=AC2,
∴AH2+4AH2=4,
∴AH=,CH=,
∴FM=CM=1,
∴S△ACH=,S△CFB=2,
∴S△ACH=S△BCF,
∴=;
(2)∵AC=2,
∴BC=4,AE=1,
∴AB==2,
∵S△ABC=AC BC=AB CH,
∴CH==,
∴AH=,
∵AD⊥AB,CH⊥AB,
∴AD∥HG,
∴=,∠DAE=∠GCE,
∵∠AED=∠CEG,AE=CE,
∴△ADE≌△CGE(ASA),
∴AD=CG,
∴=,
∴CG=,
∴AD=CG=,
∵∠DAE=∠ACH=∠BCF,
∴以B、F、C为顶点的三角形与△ADE相似,
∴或,
∴=或=,
∴BF=或.
28.解:(1)∵DE是BC垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
∵AB=AD,
∴∠ABC=∠ADB,
∴△FDB∽△ABC;
(2)∵△FDB∽△ABC,
∴==,
∴AB=2FD,
∵AB=AD,
∴AD=2FD,
∴DF=AF.
29.解:(1)∵∠ACB=90°,AC=3,BC=4,
∴AB==5.
∵AD=5t,CE=3t,
∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1.
(2)∵EF=BC=4,G是EF的中点,
∴GE=2.
当AD<AE(即t<)时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则 或 ,
∴或 ,
∴t=或t=;
当AD>AE(即t>)时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则 或 ,
∴或 ,
解得t=或t=;
综上所述,当t=或 或 或 时,△DEG与△ACB相似.
30.证明:∵AD⊥BC
∴∠ADB=90°
∵EC⊥AB
∴∠CEB=90°
∴点D和点E在以AC为直径的圆上,
∴∠BDE=∠BAC,
而∠DBE=∠ABC,
∴△BDE∽△BAC.
31.(1)证明:∵△ABD和△BCE是等边三角形,
∴AB=BD,BC=BE,∠EBC=∠ABC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中
∴△ABE≌△DBC(SAS)
∴AE=DC,
∵M、N分别为AE、CD的中点,
∴AM=AE,CN=DC
∴AM=CN;
(2)解:∵△ABE≌△DBC,
∴∠EAB=∠CDB,
在△AMB和△DNB中
∴△AMB≌△DNB(SAS),
∴∠ABM=∠DBN,
∵∠ABC=∠ABM+∠MBD=60°,
∴∠DBN+∠MBD=60°,
即∠MBN=60°;
(3)解:图中的全等三角形有:△ABM≌△DBN,△BME≌△BCN,△ABE≌△DBC;
相似三角形有:△ABD∽△BCE,△ABD∽△BMN,△BMN∽△BCE.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
