26.4解直角三角形的应用 辅导训练 2021-2022学年冀教版九年级数学上册 (Word版 含答案)
文档属性
| 名称 | 26.4解直角三角形的应用 辅导训练 2021-2022学年冀教版九年级数学上册 (Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 899.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 11:04:44 | ||
图片预览



文档简介
2021-2022学年冀教版九年级数学上册《26.4解直角三角形的应用》优生辅导训练(附答案)
1.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
A.asinx+bsinx B.acosx+bcosx
C.asinx+bcosx D.acosx+bsinx
2.某厂家新开发的一种电动车如图,它的大灯A射出的光线AB、AC与地面MN所夹的锐角分别是8°和10°.大灯A离地面的距离为lm,则该车大灯照亮地面的宽度BC是 m.(不考虑其他因素)(参考数据:sin8°≈,tan8°≈,sin10°≈,tan10°≈).
3.如图,一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从点A到点B经过的路径长为 .
4.高铁修建过程中需要经过一座小山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(A,C,D共线)处同时施工.测得∠CAB=30°,AB=8km,∠ABD=105°,求BD长.(结果精确到十分位≈1.732,≈1.414)
5.如图,某游乐场有一个直径为100米的摩天轮转盘,其最高点距离地面高度为110米,该摩天轮匀速转动一周的时间为24分钟,摩天轮上的吊舱每分钟转过的角度相同.某游客乘坐吊舱从转盘上最低点P出发,2分钟后到达点A处.
(1)求∠AOP的度数;
(2)求此时吊舱所在的位置点A距离地面的高度约为多少米?(结果精确到0.1)(参考数据:≈1.414,≈1.732)
6.某次台风来袭时,一棵笔直且垂直于地面的大树AB被刮倾斜后在C处折断倒在地上,树的顶部恰好接触到地面D处,测得∠ACD=60°,∠ADC=37°,AD=5米,求这棵大树AB的高.
(结果精确到0.1米)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.73)
7.浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图②),测量知,∠A=30°,∠C=49°,AB=60m.请你利用以上数据,求出悬索AC和支架BC的长(结果取整数).参考数据:≈1.73,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15.
.
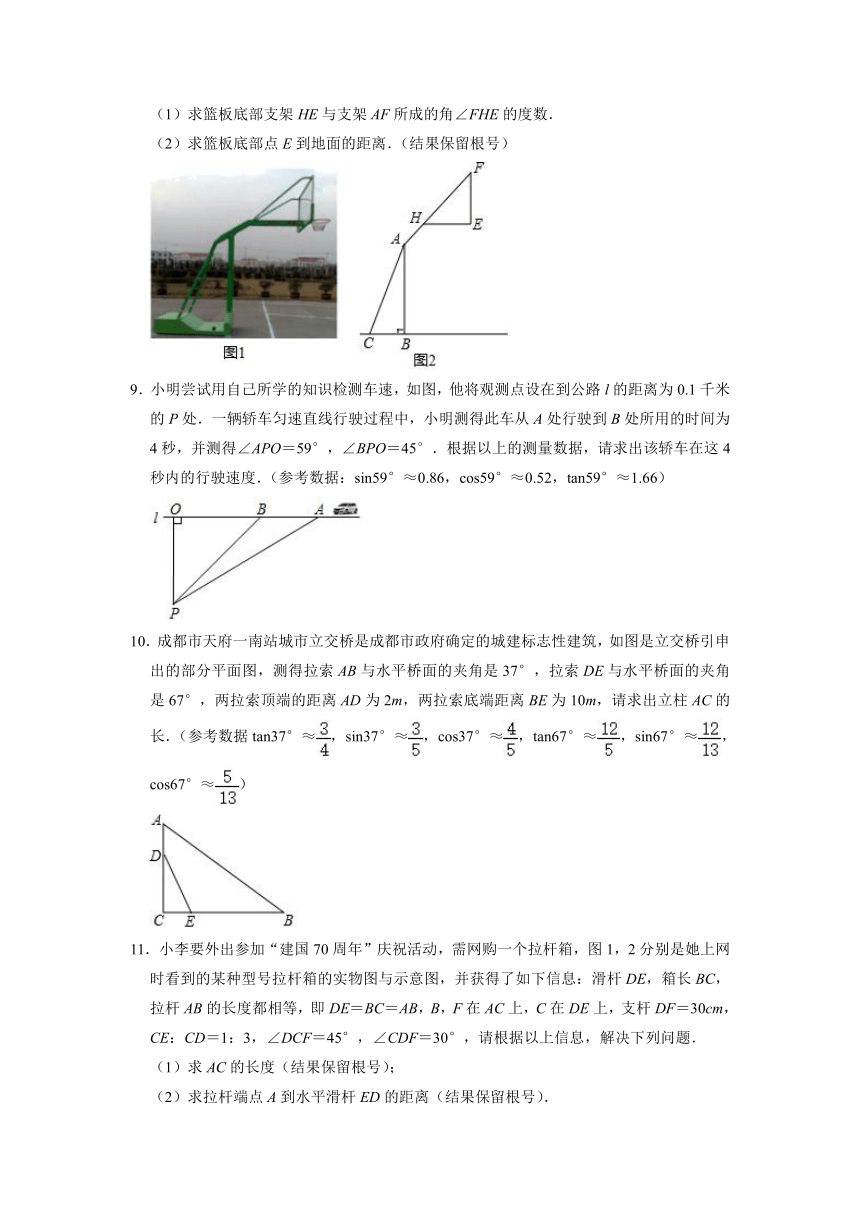
8.如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长米,HF长米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
9.小明尝试用自己所学的知识检测车速,如图,他将观测点设在到公路l的距离为0.1千米的P处.一辆轿车匀速直线行驶过程中,小明测得此车从A处行驶到B处所用的时间为4秒,并测得∠APO=59°,∠BPO=45°.根据以上的测量数据,请求出该轿车在这4秒内的行驶速度.(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
10.成都市天府一南站城市立交桥是成都市政府确定的城建标志性建筑,如图是立交桥引申出的部分平面图,测得拉索AB与水平桥面的夹角是37°,拉索DE与水平桥面的夹角是67°,两拉索顶端的距离AD为2m,两拉索底端距离BE为10m,请求出立柱AC的长.(参考数据tan37°≈,sin37°≈,cos37°≈,tan67°≈,sin67°≈,cos67°≈)
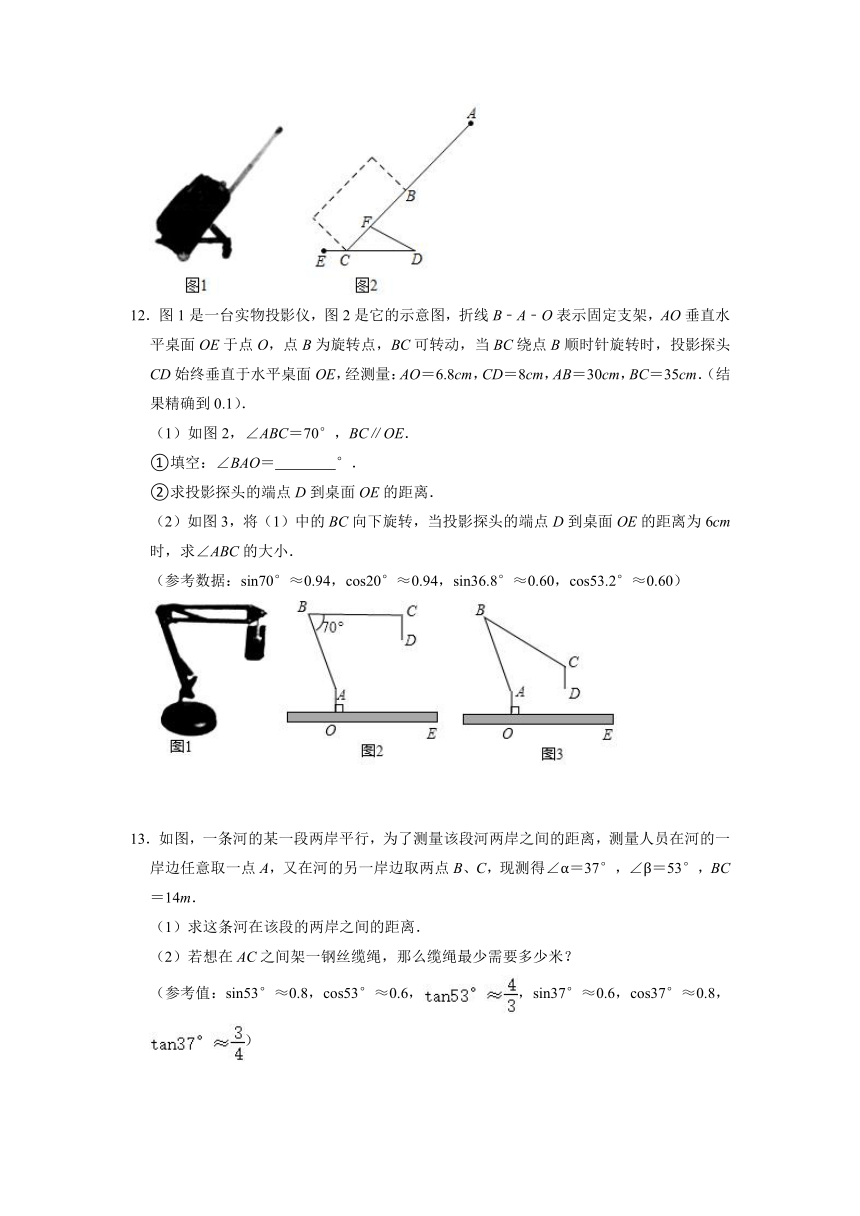
11.小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图1,2分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆DE,箱长BC,拉杆AB的长度都相等,即DE=BC=AB,B,F在AC上,C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°,请根据以上信息,解决下列问题.
(1)求AC的长度(结果保留根号);
(2)求拉杆端点A到水平滑杆ED的距离(结果保留根号).
12.图1是一台实物投影仪,图2是它的示意图,折线B﹣A﹣O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8cm,CD=8cm,AB=30cm,BC=35cm.(结果精确到0.1).
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO= °.
②求投影探头的端点D到桌面OE的距离.
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6cm时,求∠ABC的大小.
(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60)
13.如图,一条河的某一段两岸平行,为了测量该段河两岸之间的距离,测量人员在河的一岸边任意取一点A,又在河的另一岸边取两点B、C,现测得∠α=37°,∠β=53°,BC=14m.
(1)求这条河在该段的两岸之间的距离.
(2)若想在AC之间架一钢丝缆绳,那么缆绳最少需要多少米?
(参考值:sin53°≈0.8,cos53°≈0.6,,sin37°≈0.6,cos37°≈0.8,)
14.如图,小明今年国庆节到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200m,缆车由点B到点D的行驶路线与水平面夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)
15.如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.
16.如图,某小学门口有一直线马路,交警在门口设有一条宽度为4米的斑马线,为安全起见,规定车头距斑马线后端的水平距离不得低于2米,现有一旅游车在路口遇红灯刹车停下,汽车里司机与斑马线前后两端的视角分别为∠FAE=15°和∠FAD=30°,司机距车头的水平距离为0.8米,试问该旅游车停车是否符合上述安全标准?(E、D、C、B四点在平行于斑马线的同一直线上)(参考数据:,,)
17.棕北中学暑假期间将进行校园外貌环境改造.如图为校园内的两幢教学楼,它们的高AB=CD=35m,它们之间的水平距离AC=30m,现工人现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°角时,求EC的高度.
18.智能手机如果安装了一款测量软件“Smart Measure”后,就可以测量物高、宽度和面积等.如图,打开软件后将手机摄像头的屏幕准星对准脚部按键,再对准头部按键,即可测量出人体的高度.其数学原理如图②所示,测量者AB与被测量者CD都垂直于地面BC.
(1)若手机显示AC=1m,AD=1.8m,∠CAD=60°,求此时CD的高.(结果保留根号)
(2)对于一般情况,试探索手机设定的测量高度的公式:设AC=a,AD=b,∠CAD=α,即用a、b、α来表示CD.(提示:sin2α+cos2α=1)
19.综合实践课上,小明所在的小组要测量府南河的宽度.如图所示是府南河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两颗大树之间的距离均为10米,小明先用测角仪在河岸CD的M处测得∠α=30°,然后沿河岸走50米到达N点,测得∠β=60°.请你根据这些数据帮小明他们算出河宽FR.(结果保留两位有效数字,=1.732)
20.为倡导“低碳生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.
(结果精确到1cm.参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75≈3.7321)
21.如图一张长方形卡片ABCD放在宽度为10mm的横格线中,恰好四个顶点都在横格线上,已知α=32°,求长方形卡片的周长.(数据sin32°≈0.5cos32°≈0.8tan32°≈0.6)
22.如图,一座小山的山顶上有一根竖直的电线杆MN,水平直线AC与MN在同一平面,点B在AC上.用测倾器在点A处测得∠MAC=45°,∠NAC=30°,向前走10米到达点B,在点B处测得∠MBC=60°,∠NBC=45°.求:
(1)电线杆MN的长度;
(2)小山相对于水平直线AC的高度(结果保留根式).
23.如图1所示,一架长4m的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面所成的角α为60度.
(1)求AO与BO的长;
(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
①如图2所示,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端NO下滑了多少米?
②如图3所示,当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点,若∠POP′=15°,试求AA′的长.
24.观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则,即AD=csinB,AD=bsinC,于是csinB=bsinC,即,同理有:,
所以.
即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.
(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,)
25.一船在海面C处看见一灯塔A在它的正北方向,另一个灯塔B在它的北偏西60°,此船在正西航行1海里后到D,这时灯塔A、B分别在它的东北、西北方向,求这两个灯塔间的距离(结果保留根号).
26.小明在学习直角三角三角形中的三角函数时发现,在Rt△ABC中,∠C=90°,三个内角A、B、C所对的边所对的边长分别是a、b、c,由于sinA=,sinB=(已知sin90°=1)可以得到,即:在直角三角形中,每条边和它所对角的正弦值的比值相等,小明猜想:在锐角三角形中也有相同的结论.
(1)如图所示,在锐角三角形ABC中,三个内角A、B、C所对的边分别是a、b、c,AD⊥BC,BH⊥AC,请你运用直角三角形中的三角函数的有关知识验证小明的猜想.
(2)请你运用(1)中的结论,完成下题,如图,在南海某海域一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/小时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.
27.阅读材料:
一般地,当α、β为任意角时,tan(α+β)与tan(α﹣β)的值可以用下面的公式求得:tan(α±β)=.
例如:tan15°=tan(45°﹣30°)===
===2﹣.
根据以上材料,解决下列问题:
(1)求tan75°的值;
(2)都匀文峰塔,原名文笔塔,始建于明代万历年间,系五层木塔.文峰塔的木塔年久倾毁,仅存塔基.1983年,人民政府拨款维修文峰塔,成为今天的七层六面实心石塔(图1),小华想用所学知识来测量该铁塔的高度,如图2,已知小华站在离塔底中心A处5.7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.72米,请帮助小华求出文峰塔AB的高度.(精确到1米,参考数据≈1.732,≈1.414)
28.关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ﹣sinαsinβ②
tan(α+β)=③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
tan105°=tan(45°+60°)====﹣(2+).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
参考答案
1.解:作AE⊥OC于点E,作AF⊥OB于点F,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵∠ABC=∠AEC,∠BCO=x,
∴∠EAB=x,
∴∠FBA=x,
∵AB=a,AD=b,
∴FO=FB+BO=a cosx+b sinx,
故选:D.
2.解:作AD⊥MN,垂足为D.
在Rt△ADC中,=tan10°,
即=tan10°,
CD=,
Rt△ABD中,=tan8°,
即=tan8°,
=tan8°,
解得BC≈1.4m.
故答案为1.4m.
3.解:如图所示,
延长AC交x轴于B′.则点B、B′关于y轴对称,CB=CB′.
作AD⊥x轴于D点.则AD=3,DB′=3+1=4.
∴AB′=AC+CB′=AC+CB=5.
即光线从点A到点B经过的路径长为5.
4.解:作BE⊥AD于点E,
∵∠CAB=30°,AB=8km,
∴∠ABE=60°,BE=4km,
∵∠ABD=105°,
∴∠EBD=45°,
∴∠EDB=45°,
∴BE=DE=4km,
∴BD=≈5.7(km),
即BD的长是5.7km.
5.解:(1)∵吊舱每分钟转过的角度==15°,
∴2分钟转过的角度为30°,
∴∠AOP的度数为30°;
(2)如图,过点A作AH⊥MN于H,
在Rt△OAH中,∠AOH=30°,
∴OH=OA cos∠AOH=50×=25,
∴HM=HP+PM=OP﹣OH+MN﹣MP=50﹣25+110﹣100=60﹣25≈16.7(米).
答:此时吊舱所在的位置点A距离地面的高度约为16.7米.
6.解:过点A作AE⊥CD于点E,则∠AEC=∠AED=90°.
∵在Rt△AED中,∠ADC=37°,
∴cos37°==≈0.8,
∴DE≈4,
∵sin37°==≈0.6,
∴AE≈3,
在Rt△AEC中,
∵∠CAE=90°﹣∠ACE=90°﹣60°=30°,
∴CE=AE=,
∴AC=2CE=2,
∴AB=AC+CE+ED=2++4=3+4≈9.2(米).
答:这棵大树AB原来的高度约是9.2米.
7.解:过点B作BD⊥AC于点D,
∵∠A=30°,AB=60,
∴BD=AB=30,
∴AD=BD=30,
在Rt△CBD中,
tan49°=,sin49°=,
∴CD≈26,BC≈40,
∴AC=AD+CD≈78.
8.解:(1)在Rt△EFH中,cos∠FHE==,
∴∠FHE=45°,
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB=,
∴AB=BCtan60°=1×=,
∴GM=AB=,
在Rt△ANH中,∠FAN=∠FHE=45°,
∴HN=AHsin45°=×=,
∴EM=EG+GM=+,
答:篮板底部点E到地面的距离是(+)米.
9.解:在Rt△BOP中,∠BPO=45°,PO=0.1
∴BO=PO=0.1,
在Rt△AOP中,∠APO=59°,PO=0.1,
∴AO=PO tan59°≈0.1×1.66=0.166,
∴AB=AO﹣BO=0.166﹣0.1=0.066,
∴0.066÷=59.4,
答:该轿车在这4秒内的行驶速度为每小时59.4千米.
10.解:设CE=xm,则BC=(10+x)m,
在Rt△CDE中,∵∠DEC=67°,
∴CD=CE tan67°=x,
在Rt△ABC中,∵∠B=37°,
∴AC=BC tan37°=×(10+x),
∴AD=AC﹣CD=×(10+x)﹣x=2,
解得:x=,
∴AC=AD+CD=2+×=10(m),
答:立柱AC的长为10m.
11.解:(1)过F作FH⊥DE于H,
∴∠FHC=∠FHD=90°,
∵∠FDC=30°,DF=30,
∴FH=DF=15,DH=DF=15(cm),
∵∠FCH=45°,
∴CH=FH=15(cm),
∴(cm),
∵CE:CD=1:3,
∴DE=CD=(20+20)(cm),
∵AB=BC=DE,
∴AC=(40+40)cm;
(2)过A作AG⊥ED交ED的延长线于G,
∵∠ACG=45°,
∴AG=AC=(20+20)(cm),
答:拉杆端点A到水平滑杆ED的距离为(20+20)cm.
12.解:(1)①过点A作AG∥BC,如图1,则∠BAG=∠ABC=70°,
∵BC∥OE,
∴AG∥OE,
∴∠GAO=∠AOE=90°,
∴∠BAO=90°+70°=160°,
故答案为:160;
②过点A作AF⊥BC于点F,如图2,
则AF=AB sin∠ABF=30sin70°≈28.2(cm),
∴投影探头的端点D到桌面OE的距离为:AF+OA﹣CD=28.2+6.8﹣8=27.0(cm);
(2)过点DE⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过A作AF⊥BM于点F,如图3,
则∠MBA=70°,AF=28.2cm,DH=6cm,BC=35cm,CD=8cm,
∴CM=AF+AO﹣DH﹣CD=28.2+6.8﹣6﹣8=21(cm),
∴sin∠MBC=,
∴∠MBC=36.8°,
∴∠ABC=∠ABM﹣∠MBC=33.2°.
13.解:(1)过点A作AD⊥BC,垂足为D,则AD的长即为两岸之间的距离.
在Rt△ABD中,tan∠ABD=tanα==,
∴BD=AD;
在Rt△ACD中,tan∠ACD=tanβ==,
∴CD=AD.
又∵AC=AD﹣CD=AD﹣AD=14,
∴AD=24,即这条河在该段的两岸之间的距离为24米.
(2)在Rt△ACD中,sin∠ACD=sinα=≈0.8,
解得:AC≈30.
答:钢丝缆绳最少需要30米.
14.解:Rt△ABC中,斜边AB=200米,∠α=16°,BC=AB sinα=200×sin16°≈54(m),
Rt△BDF中,斜边BD=200米,∠β=42°,
DF=BD sinβ=200×sin42°≈132,
因此缆车垂直上升的距离应该是BC+DF=186(米).
答:缆车垂直上升了186米.
15.解:如图,延长OD,BC交于点P.
由题意可得OB=11米,CD=2米,
∵∠ODC=∠B=90°,∠BCD=120°
∴∠P=30°,
∴在直角△CPD中,DP=DC tan30°=2m,PC=CD÷(sin30°)=4米,
∵∠P=∠P,∠PDC=∠B=90°,
∴△PDC∽△PBO,
∴
∴PB===11米,
∴BC=PB﹣PC=(11﹣4)米.
解法二:求出PB==11,PC==4,
∴BC=PB﹣PC=(11﹣4)米.
16.解:∵∠FAE=15°,∠FAD=30°,
∴∠EAD=15°,
∵AF∥BE,
∴∠AED=∠FAE=15°,∠ADB=∠FAD=30°,
设AB=x,
则在Rt△AEB中,
EB==,
∵ED=4,ED+BD=EB,
∴BD=﹣4,
在Rt△ADB中,
BD==,
∴﹣4=,
即(﹣)x=4,解得x=2,
∴BD==2,
∵BD=CD+BC=CD+0.8,
∴CD=2﹣0.8≈2×1.732﹣0.8≈2.7>2,故符合标准.
答:该旅游车停车符合规定的安全标准.
17.解:∵太阳光与水平线的夹角为30°,
∴∠BEF=30°,
∵AC=EF=30m,
∴BF=EF tan30°=30×=10(m),
∴EC=CD﹣BF=(35﹣10)m.
18.解:(1)作CH⊥AD于点H.
在Rt△ACH中,∵AC=1,∠CAH=60°,
∴AH=,CH=.
∵AD=1.8,
∴HD=1.3.
∴CD=(m);
(2)同上可得,AH=acosα,CH=asinα.
∵AD=b,
∴HD=b﹣acosα.
∴CD==.
19.解:过点F作FG∥EM交CD于G,则MG=EF=20米.
∵∠FGN=∠α=30°.
∴∠GFN=∠β﹣∠FGN=60°﹣30°=30°.
∴∠FGN=∠GFN,
∴FN=GN=50﹣20=30(米).
在Rt△FNR中,
FR=FN×sinβ=30×sin60°=30×≈26(米).
答:河宽FR约为26米.
20.解:(1)∵在RT△ACD中,AC=45cm,DC=60cm,
∴AD==75,
∴车架档AD的长为75cm,
(2)过点E作EF⊥AB,垂足为点F,
∵AE=AC+CE=45+20(cm)
∴EF=AEsin75°=(45+20)sin75°≈62.7835≈63cm,
∴车座点E到车架档AB的距离是63cm.
21.解:作AF⊥l4,交l2于E,交l4于F.
则△ABE和△AFD均为直角三角形.
在Rt△ABE中,∠ABE=∠α=32°,
sin∠ABE=,(3分)
∴AB===40.
∵∠FAD=90°﹣∠BAE=90°﹣∠BAE=∠α,
∴∠FAD=∠α=32°.
在Rt△AFD中,cos∠FAD=,
AD===50.
∴长方形卡片ABCD的周长为(40+50)×2=180(mm).
22.解:(1)延长MN交AC于D,则MD⊥AC,
在Rt△MAD中,∠MAC=45°,
∴DA=DM,
在Rt△NBD中,∠NBC=45°,
∴DB=DN,
∴DA﹣DB=DM﹣DN,即MN=AB=10米;
(2)在Rt△NAD中,∠NAD=30°,
∴ND=AD tan∠NAD=AD,
∴AD﹣AD=10,
解得:AD=15+5,
∴ND=AD=(5+5)米,
答:小山相对于水平直线AC的高度为(5+5)米.
23.解:(1)BO=AB cos60°=4×=2(m)
AO=AB sin60°=4×=2(m)
答:BO=2m;AO=2m.
(2)①设AC=2x,BD=3x,在Rt△COD中,OC=2﹣2x,OD=2+3x,CD=4m.
根据勾股定理有OC2+OD2=CD2.
∴(2﹣2x)2+(2+3x)2=42.
∴13x2+(12﹣8)x=0.
∵x≠0,
∴13x+12﹣8=0,
∴x=m.
∴AC=2x=m.
答:梯子顶端A沿NO下滑了m.
②∵P点和P′点分别是Rt△AOB的斜边AB与Rt△A′OB′的斜边A′B′的中点.
∴PA=PO,P′A′=P′O.
∴∠PAO=∠AOP,∠P′A′O=∠A′OP′.
∴∠P′A′O﹣∠PAO=∠A′OP′﹣∠AOP.
∴∠P′A′O﹣∠PAO=∠POP′=15°.
又∵∠PAO=30°.
∴∠P′A′O=45°.
∴A′O=A′B′ cos45°=4×=2(m).
∴AA′=AO﹣A′O=(2﹣2)m.
24.解:(1)由正弦定理得:∠A=60°,AC=20;
故答案为:60°,20;
(2)如图,依题意:BC=40×0.5=20(海里)
∵CD∥BE,∴∠DCB+∠CBE=180°.
∵∠DCB=30°,∴∠CBE=150°.
∵∠ABE=75°,∴∠ABC=75°.
∴∠A=45°.
在△ABC中,,
即,
解之得:AB=10≈24.49海里.
所以渔政204船距钓鱼岛A的距离约为24.49海里.
25.解:如图所示:过点B作BE⊥CD于点E,
∵∠1=60°,∠2=∠3=45°,∠ADC=∠BDE=45°,
∴AC=DC=1,BE=DE,∠ADB=90°,∠BCE=30°,
∴AD==,tan30°=,
设BE=x,则ED=x,
故=,
解得:x=,
则BD2=2x2=2×()2=2+,
AD2=2,
故AB2=4+,
则AB=(海里),
答:这两个灯塔间的距离为海里.
26.解:(1)如图(2),在Rt△ABH中,∵sinA=,
∴BH=csinA,
在Rt△BCH中,∵sinC=,
∴BH=asinC,
∴csinA=asinC,
∴=,
同理可得=,
∴==;
(2)如图(3),∠1=90°﹣75°=15°,∠2=90°﹣30°=60°,BC=60×=30,
∴∠ABC=75°,
而∠ACB=60°,
∴∠A=180°﹣60°﹣75°=45°,
∵=,
∴=,
∴AB==15,
此时货轮距灯塔A的距离AB为15海里.
27.解:(1)tan75°=tan(45°+30°)====2+;
(2)如图2,易得DE=CA=5.7,AE=CD=1.72,
在Rt△BDE中,∵tan∠BDE=,
∴BE=DEtan75°=5.7×(2+)≈21.2724,
∴AB=BE+AE=21.2724+1.72≈23(m).
答:文峰塔AB的高度约为23m.
28.解:由于α=60°,β=75°,BC=42,
则AB=BC tanβ=42tan75°=42 =42 =42(),
A、D垂直距离为BC tanα=42,
∴CD=AB﹣42=84(米).
答:建筑物CD的高为84米.
1.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
A.asinx+bsinx B.acosx+bcosx
C.asinx+bcosx D.acosx+bsinx
2.某厂家新开发的一种电动车如图,它的大灯A射出的光线AB、AC与地面MN所夹的锐角分别是8°和10°.大灯A离地面的距离为lm,则该车大灯照亮地面的宽度BC是 m.(不考虑其他因素)(参考数据:sin8°≈,tan8°≈,sin10°≈,tan10°≈).
3.如图,一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从点A到点B经过的路径长为 .
4.高铁修建过程中需要经过一座小山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(A,C,D共线)处同时施工.测得∠CAB=30°,AB=8km,∠ABD=105°,求BD长.(结果精确到十分位≈1.732,≈1.414)
5.如图,某游乐场有一个直径为100米的摩天轮转盘,其最高点距离地面高度为110米,该摩天轮匀速转动一周的时间为24分钟,摩天轮上的吊舱每分钟转过的角度相同.某游客乘坐吊舱从转盘上最低点P出发,2分钟后到达点A处.
(1)求∠AOP的度数;
(2)求此时吊舱所在的位置点A距离地面的高度约为多少米?(结果精确到0.1)(参考数据:≈1.414,≈1.732)
6.某次台风来袭时,一棵笔直且垂直于地面的大树AB被刮倾斜后在C处折断倒在地上,树的顶部恰好接触到地面D处,测得∠ACD=60°,∠ADC=37°,AD=5米,求这棵大树AB的高.
(结果精确到0.1米)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.73)
7.浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图②),测量知,∠A=30°,∠C=49°,AB=60m.请你利用以上数据,求出悬索AC和支架BC的长(结果取整数).参考数据:≈1.73,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15.
.
8.如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长米,HF长米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
9.小明尝试用自己所学的知识检测车速,如图,他将观测点设在到公路l的距离为0.1千米的P处.一辆轿车匀速直线行驶过程中,小明测得此车从A处行驶到B处所用的时间为4秒,并测得∠APO=59°,∠BPO=45°.根据以上的测量数据,请求出该轿车在这4秒内的行驶速度.(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
10.成都市天府一南站城市立交桥是成都市政府确定的城建标志性建筑,如图是立交桥引申出的部分平面图,测得拉索AB与水平桥面的夹角是37°,拉索DE与水平桥面的夹角是67°,两拉索顶端的距离AD为2m,两拉索底端距离BE为10m,请求出立柱AC的长.(参考数据tan37°≈,sin37°≈,cos37°≈,tan67°≈,sin67°≈,cos67°≈)
11.小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图1,2分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆DE,箱长BC,拉杆AB的长度都相等,即DE=BC=AB,B,F在AC上,C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°,请根据以上信息,解决下列问题.
(1)求AC的长度(结果保留根号);
(2)求拉杆端点A到水平滑杆ED的距离(结果保留根号).
12.图1是一台实物投影仪,图2是它的示意图,折线B﹣A﹣O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.8cm,CD=8cm,AB=30cm,BC=35cm.(结果精确到0.1).
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO= °.
②求投影探头的端点D到桌面OE的距离.
(2)如图3,将(1)中的BC向下旋转,当投影探头的端点D到桌面OE的距离为6cm时,求∠ABC的大小.
(参考数据:sin70°≈0.94,cos20°≈0.94,sin36.8°≈0.60,cos53.2°≈0.60)
13.如图,一条河的某一段两岸平行,为了测量该段河两岸之间的距离,测量人员在河的一岸边任意取一点A,又在河的另一岸边取两点B、C,现测得∠α=37°,∠β=53°,BC=14m.
(1)求这条河在该段的两岸之间的距离.
(2)若想在AC之间架一钢丝缆绳,那么缆绳最少需要多少米?
(参考值:sin53°≈0.8,cos53°≈0.6,,sin37°≈0.6,cos37°≈0.8,)
14.如图,小明今年国庆节到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200m,缆车由点B到点D的行驶路线与水平面夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)
15.如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.
16.如图,某小学门口有一直线马路,交警在门口设有一条宽度为4米的斑马线,为安全起见,规定车头距斑马线后端的水平距离不得低于2米,现有一旅游车在路口遇红灯刹车停下,汽车里司机与斑马线前后两端的视角分别为∠FAE=15°和∠FAD=30°,司机距车头的水平距离为0.8米,试问该旅游车停车是否符合上述安全标准?(E、D、C、B四点在平行于斑马线的同一直线上)(参考数据:,,)
17.棕北中学暑假期间将进行校园外貌环境改造.如图为校园内的两幢教学楼,它们的高AB=CD=35m,它们之间的水平距离AC=30m,现工人现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°角时,求EC的高度.
18.智能手机如果安装了一款测量软件“Smart Measure”后,就可以测量物高、宽度和面积等.如图,打开软件后将手机摄像头的屏幕准星对准脚部按键,再对准头部按键,即可测量出人体的高度.其数学原理如图②所示,测量者AB与被测量者CD都垂直于地面BC.
(1)若手机显示AC=1m,AD=1.8m,∠CAD=60°,求此时CD的高.(结果保留根号)
(2)对于一般情况,试探索手机设定的测量高度的公式:设AC=a,AD=b,∠CAD=α,即用a、b、α来表示CD.(提示:sin2α+cos2α=1)
19.综合实践课上,小明所在的小组要测量府南河的宽度.如图所示是府南河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两颗大树之间的距离均为10米,小明先用测角仪在河岸CD的M处测得∠α=30°,然后沿河岸走50米到达N点,测得∠β=60°.请你根据这些数据帮小明他们算出河宽FR.(结果保留两位有效数字,=1.732)
20.为倡导“低碳生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.
(结果精确到1cm.参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75≈3.7321)
21.如图一张长方形卡片ABCD放在宽度为10mm的横格线中,恰好四个顶点都在横格线上,已知α=32°,求长方形卡片的周长.(数据sin32°≈0.5cos32°≈0.8tan32°≈0.6)
22.如图,一座小山的山顶上有一根竖直的电线杆MN,水平直线AC与MN在同一平面,点B在AC上.用测倾器在点A处测得∠MAC=45°,∠NAC=30°,向前走10米到达点B,在点B处测得∠MBC=60°,∠NBC=45°.求:
(1)电线杆MN的长度;
(2)小山相对于水平直线AC的高度(结果保留根式).
23.如图1所示,一架长4m的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面所成的角α为60度.
(1)求AO与BO的长;
(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
①如图2所示,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端NO下滑了多少米?
②如图3所示,当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点,若∠POP′=15°,试求AA′的长.
24.观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则,即AD=csinB,AD=bsinC,于是csinB=bsinC,即,同理有:,
所以.
即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.
(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,)
25.一船在海面C处看见一灯塔A在它的正北方向,另一个灯塔B在它的北偏西60°,此船在正西航行1海里后到D,这时灯塔A、B分别在它的东北、西北方向,求这两个灯塔间的距离(结果保留根号).
26.小明在学习直角三角三角形中的三角函数时发现,在Rt△ABC中,∠C=90°,三个内角A、B、C所对的边所对的边长分别是a、b、c,由于sinA=,sinB=(已知sin90°=1)可以得到,即:在直角三角形中,每条边和它所对角的正弦值的比值相等,小明猜想:在锐角三角形中也有相同的结论.
(1)如图所示,在锐角三角形ABC中,三个内角A、B、C所对的边分别是a、b、c,AD⊥BC,BH⊥AC,请你运用直角三角形中的三角函数的有关知识验证小明的猜想.
(2)请你运用(1)中的结论,完成下题,如图,在南海某海域一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/小时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.
27.阅读材料:
一般地,当α、β为任意角时,tan(α+β)与tan(α﹣β)的值可以用下面的公式求得:tan(α±β)=.
例如:tan15°=tan(45°﹣30°)===
===2﹣.
根据以上材料,解决下列问题:
(1)求tan75°的值;
(2)都匀文峰塔,原名文笔塔,始建于明代万历年间,系五层木塔.文峰塔的木塔年久倾毁,仅存塔基.1983年,人民政府拨款维修文峰塔,成为今天的七层六面实心石塔(图1),小华想用所学知识来测量该铁塔的高度,如图2,已知小华站在离塔底中心A处5.7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.72米,请帮助小华求出文峰塔AB的高度.(精确到1米,参考数据≈1.732,≈1.414)
28.关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ﹣sinαsinβ②
tan(α+β)=③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
tan105°=tan(45°+60°)====﹣(2+).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
参考答案
1.解:作AE⊥OC于点E,作AF⊥OB于点F,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵∠ABC=∠AEC,∠BCO=x,
∴∠EAB=x,
∴∠FBA=x,
∵AB=a,AD=b,
∴FO=FB+BO=a cosx+b sinx,
故选:D.
2.解:作AD⊥MN,垂足为D.
在Rt△ADC中,=tan10°,
即=tan10°,
CD=,
Rt△ABD中,=tan8°,
即=tan8°,
=tan8°,
解得BC≈1.4m.
故答案为1.4m.
3.解:如图所示,
延长AC交x轴于B′.则点B、B′关于y轴对称,CB=CB′.
作AD⊥x轴于D点.则AD=3,DB′=3+1=4.
∴AB′=AC+CB′=AC+CB=5.
即光线从点A到点B经过的路径长为5.
4.解:作BE⊥AD于点E,
∵∠CAB=30°,AB=8km,
∴∠ABE=60°,BE=4km,
∵∠ABD=105°,
∴∠EBD=45°,
∴∠EDB=45°,
∴BE=DE=4km,
∴BD=≈5.7(km),
即BD的长是5.7km.
5.解:(1)∵吊舱每分钟转过的角度==15°,
∴2分钟转过的角度为30°,
∴∠AOP的度数为30°;
(2)如图,过点A作AH⊥MN于H,
在Rt△OAH中,∠AOH=30°,
∴OH=OA cos∠AOH=50×=25,
∴HM=HP+PM=OP﹣OH+MN﹣MP=50﹣25+110﹣100=60﹣25≈16.7(米).
答:此时吊舱所在的位置点A距离地面的高度约为16.7米.
6.解:过点A作AE⊥CD于点E,则∠AEC=∠AED=90°.
∵在Rt△AED中,∠ADC=37°,
∴cos37°==≈0.8,
∴DE≈4,
∵sin37°==≈0.6,
∴AE≈3,
在Rt△AEC中,
∵∠CAE=90°﹣∠ACE=90°﹣60°=30°,
∴CE=AE=,
∴AC=2CE=2,
∴AB=AC+CE+ED=2++4=3+4≈9.2(米).
答:这棵大树AB原来的高度约是9.2米.
7.解:过点B作BD⊥AC于点D,
∵∠A=30°,AB=60,
∴BD=AB=30,
∴AD=BD=30,
在Rt△CBD中,
tan49°=,sin49°=,
∴CD≈26,BC≈40,
∴AC=AD+CD≈78.
8.解:(1)在Rt△EFH中,cos∠FHE==,
∴∠FHE=45°,
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB=,
∴AB=BCtan60°=1×=,
∴GM=AB=,
在Rt△ANH中,∠FAN=∠FHE=45°,
∴HN=AHsin45°=×=,
∴EM=EG+GM=+,
答:篮板底部点E到地面的距离是(+)米.
9.解:在Rt△BOP中,∠BPO=45°,PO=0.1
∴BO=PO=0.1,
在Rt△AOP中,∠APO=59°,PO=0.1,
∴AO=PO tan59°≈0.1×1.66=0.166,
∴AB=AO﹣BO=0.166﹣0.1=0.066,
∴0.066÷=59.4,
答:该轿车在这4秒内的行驶速度为每小时59.4千米.
10.解:设CE=xm,则BC=(10+x)m,
在Rt△CDE中,∵∠DEC=67°,
∴CD=CE tan67°=x,
在Rt△ABC中,∵∠B=37°,
∴AC=BC tan37°=×(10+x),
∴AD=AC﹣CD=×(10+x)﹣x=2,
解得:x=,
∴AC=AD+CD=2+×=10(m),
答:立柱AC的长为10m.
11.解:(1)过F作FH⊥DE于H,
∴∠FHC=∠FHD=90°,
∵∠FDC=30°,DF=30,
∴FH=DF=15,DH=DF=15(cm),
∵∠FCH=45°,
∴CH=FH=15(cm),
∴(cm),
∵CE:CD=1:3,
∴DE=CD=(20+20)(cm),
∵AB=BC=DE,
∴AC=(40+40)cm;
(2)过A作AG⊥ED交ED的延长线于G,
∵∠ACG=45°,
∴AG=AC=(20+20)(cm),
答:拉杆端点A到水平滑杆ED的距离为(20+20)cm.
12.解:(1)①过点A作AG∥BC,如图1,则∠BAG=∠ABC=70°,
∵BC∥OE,
∴AG∥OE,
∴∠GAO=∠AOE=90°,
∴∠BAO=90°+70°=160°,
故答案为:160;
②过点A作AF⊥BC于点F,如图2,
则AF=AB sin∠ABF=30sin70°≈28.2(cm),
∴投影探头的端点D到桌面OE的距离为:AF+OA﹣CD=28.2+6.8﹣8=27.0(cm);
(2)过点DE⊥OE于点H,过点B作BM⊥CD,与DC延长线相交于点M,过A作AF⊥BM于点F,如图3,
则∠MBA=70°,AF=28.2cm,DH=6cm,BC=35cm,CD=8cm,
∴CM=AF+AO﹣DH﹣CD=28.2+6.8﹣6﹣8=21(cm),
∴sin∠MBC=,
∴∠MBC=36.8°,
∴∠ABC=∠ABM﹣∠MBC=33.2°.
13.解:(1)过点A作AD⊥BC,垂足为D,则AD的长即为两岸之间的距离.
在Rt△ABD中,tan∠ABD=tanα==,
∴BD=AD;
在Rt△ACD中,tan∠ACD=tanβ==,
∴CD=AD.
又∵AC=AD﹣CD=AD﹣AD=14,
∴AD=24,即这条河在该段的两岸之间的距离为24米.
(2)在Rt△ACD中,sin∠ACD=sinα=≈0.8,
解得:AC≈30.
答:钢丝缆绳最少需要30米.
14.解:Rt△ABC中,斜边AB=200米,∠α=16°,BC=AB sinα=200×sin16°≈54(m),
Rt△BDF中,斜边BD=200米,∠β=42°,
DF=BD sinβ=200×sin42°≈132,
因此缆车垂直上升的距离应该是BC+DF=186(米).
答:缆车垂直上升了186米.
15.解:如图,延长OD,BC交于点P.
由题意可得OB=11米,CD=2米,
∵∠ODC=∠B=90°,∠BCD=120°
∴∠P=30°,
∴在直角△CPD中,DP=DC tan30°=2m,PC=CD÷(sin30°)=4米,
∵∠P=∠P,∠PDC=∠B=90°,
∴△PDC∽△PBO,
∴
∴PB===11米,
∴BC=PB﹣PC=(11﹣4)米.
解法二:求出PB==11,PC==4,
∴BC=PB﹣PC=(11﹣4)米.
16.解:∵∠FAE=15°,∠FAD=30°,
∴∠EAD=15°,
∵AF∥BE,
∴∠AED=∠FAE=15°,∠ADB=∠FAD=30°,
设AB=x,
则在Rt△AEB中,
EB==,
∵ED=4,ED+BD=EB,
∴BD=﹣4,
在Rt△ADB中,
BD==,
∴﹣4=,
即(﹣)x=4,解得x=2,
∴BD==2,
∵BD=CD+BC=CD+0.8,
∴CD=2﹣0.8≈2×1.732﹣0.8≈2.7>2,故符合标准.
答:该旅游车停车符合规定的安全标准.
17.解:∵太阳光与水平线的夹角为30°,
∴∠BEF=30°,
∵AC=EF=30m,
∴BF=EF tan30°=30×=10(m),
∴EC=CD﹣BF=(35﹣10)m.
18.解:(1)作CH⊥AD于点H.
在Rt△ACH中,∵AC=1,∠CAH=60°,
∴AH=,CH=.
∵AD=1.8,
∴HD=1.3.
∴CD=(m);
(2)同上可得,AH=acosα,CH=asinα.
∵AD=b,
∴HD=b﹣acosα.
∴CD==.
19.解:过点F作FG∥EM交CD于G,则MG=EF=20米.
∵∠FGN=∠α=30°.
∴∠GFN=∠β﹣∠FGN=60°﹣30°=30°.
∴∠FGN=∠GFN,
∴FN=GN=50﹣20=30(米).
在Rt△FNR中,
FR=FN×sinβ=30×sin60°=30×≈26(米).
答:河宽FR约为26米.
20.解:(1)∵在RT△ACD中,AC=45cm,DC=60cm,
∴AD==75,
∴车架档AD的长为75cm,
(2)过点E作EF⊥AB,垂足为点F,
∵AE=AC+CE=45+20(cm)
∴EF=AEsin75°=(45+20)sin75°≈62.7835≈63cm,
∴车座点E到车架档AB的距离是63cm.
21.解:作AF⊥l4,交l2于E,交l4于F.
则△ABE和△AFD均为直角三角形.
在Rt△ABE中,∠ABE=∠α=32°,
sin∠ABE=,(3分)
∴AB===40.
∵∠FAD=90°﹣∠BAE=90°﹣∠BAE=∠α,
∴∠FAD=∠α=32°.
在Rt△AFD中,cos∠FAD=,
AD===50.
∴长方形卡片ABCD的周长为(40+50)×2=180(mm).
22.解:(1)延长MN交AC于D,则MD⊥AC,
在Rt△MAD中,∠MAC=45°,
∴DA=DM,
在Rt△NBD中,∠NBC=45°,
∴DB=DN,
∴DA﹣DB=DM﹣DN,即MN=AB=10米;
(2)在Rt△NAD中,∠NAD=30°,
∴ND=AD tan∠NAD=AD,
∴AD﹣AD=10,
解得:AD=15+5,
∴ND=AD=(5+5)米,
答:小山相对于水平直线AC的高度为(5+5)米.
23.解:(1)BO=AB cos60°=4×=2(m)
AO=AB sin60°=4×=2(m)
答:BO=2m;AO=2m.
(2)①设AC=2x,BD=3x,在Rt△COD中,OC=2﹣2x,OD=2+3x,CD=4m.
根据勾股定理有OC2+OD2=CD2.
∴(2﹣2x)2+(2+3x)2=42.
∴13x2+(12﹣8)x=0.
∵x≠0,
∴13x+12﹣8=0,
∴x=m.
∴AC=2x=m.
答:梯子顶端A沿NO下滑了m.
②∵P点和P′点分别是Rt△AOB的斜边AB与Rt△A′OB′的斜边A′B′的中点.
∴PA=PO,P′A′=P′O.
∴∠PAO=∠AOP,∠P′A′O=∠A′OP′.
∴∠P′A′O﹣∠PAO=∠A′OP′﹣∠AOP.
∴∠P′A′O﹣∠PAO=∠POP′=15°.
又∵∠PAO=30°.
∴∠P′A′O=45°.
∴A′O=A′B′ cos45°=4×=2(m).
∴AA′=AO﹣A′O=(2﹣2)m.
24.解:(1)由正弦定理得:∠A=60°,AC=20;
故答案为:60°,20;
(2)如图,依题意:BC=40×0.5=20(海里)
∵CD∥BE,∴∠DCB+∠CBE=180°.
∵∠DCB=30°,∴∠CBE=150°.
∵∠ABE=75°,∴∠ABC=75°.
∴∠A=45°.
在△ABC中,,
即,
解之得:AB=10≈24.49海里.
所以渔政204船距钓鱼岛A的距离约为24.49海里.
25.解:如图所示:过点B作BE⊥CD于点E,
∵∠1=60°,∠2=∠3=45°,∠ADC=∠BDE=45°,
∴AC=DC=1,BE=DE,∠ADB=90°,∠BCE=30°,
∴AD==,tan30°=,
设BE=x,则ED=x,
故=,
解得:x=,
则BD2=2x2=2×()2=2+,
AD2=2,
故AB2=4+,
则AB=(海里),
答:这两个灯塔间的距离为海里.
26.解:(1)如图(2),在Rt△ABH中,∵sinA=,
∴BH=csinA,
在Rt△BCH中,∵sinC=,
∴BH=asinC,
∴csinA=asinC,
∴=,
同理可得=,
∴==;
(2)如图(3),∠1=90°﹣75°=15°,∠2=90°﹣30°=60°,BC=60×=30,
∴∠ABC=75°,
而∠ACB=60°,
∴∠A=180°﹣60°﹣75°=45°,
∵=,
∴=,
∴AB==15,
此时货轮距灯塔A的距离AB为15海里.
27.解:(1)tan75°=tan(45°+30°)====2+;
(2)如图2,易得DE=CA=5.7,AE=CD=1.72,
在Rt△BDE中,∵tan∠BDE=,
∴BE=DEtan75°=5.7×(2+)≈21.2724,
∴AB=BE+AE=21.2724+1.72≈23(m).
答:文峰塔AB的高度约为23m.
28.解:由于α=60°,β=75°,BC=42,
则AB=BC tanβ=42tan75°=42 =42 =42(),
A、D垂直距离为BC tanα=42,
∴CD=AB﹣42=84(米).
答:建筑物CD的高为84米.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
