26.4解直角三角形的应用 同步练习2020-2021学年冀教版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 26.4解直角三角形的应用 同步练习2020-2021学年冀教版数学九年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 686.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 11:05:39 | ||
图片预览



文档简介
解直角三角形的应用
一、单选题
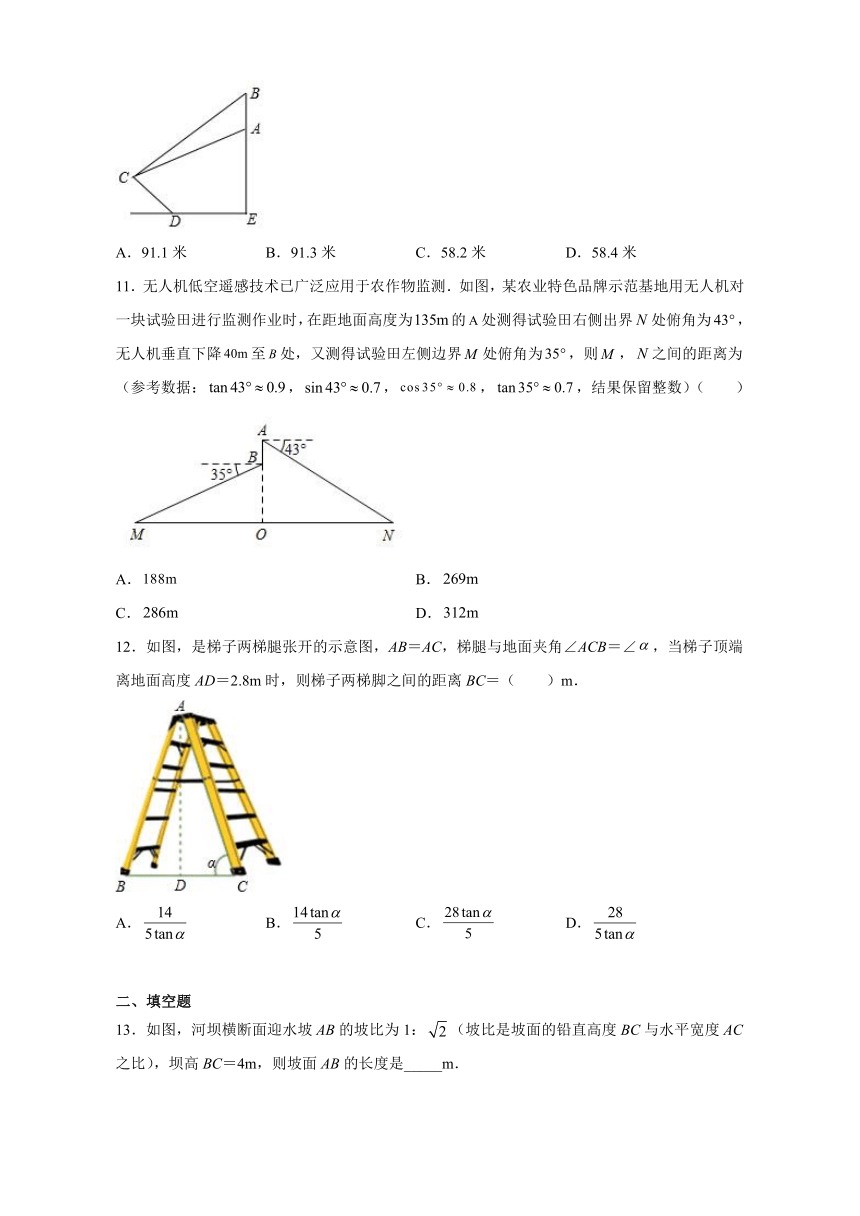
1.如图,飞机于空中A处测得目标B处的俯角为α,此时飞机的高度AC为a米,则AB的距离为( )米
A.atanα B. C. D.
2.如图,岛P位于岛Q的正西方,P、Q两岛间的距离为海里,由岛P、Q分别测得船R位于南偏东和南偏西方向上,则船R到岛P的距离为( )
A.海里 B.海里 C.20海里 D.40海里
3.如图要测量小河两岸相对的两点P、A的距离,可以在小河边取的垂线上的一点C,测得米,,则小河宽为( )米
A. B. C. D.
4.小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高为1.55米,她先站在处看路灯顶端的仰角为35°,再往前走3米站在处,看路灯顶端的仰角为65°,则路灯顶端到地而的距离为(已知,,,,,)( )
A.3.2米 B.3.9米 C.4.7米 D.5.4米
5.重庆移动为了提升网络信号,修建了多个5G信号塔,如图,垂直于水平面的信号塔建在垂直于水平面的悬崖边点处.某测量员从山脚点出发沿水平方向前行78米 到点(点,,在同一直线上),再沿斜坡方向前行78米到点(点,,,,在同一平面内),在点处测得信号塔顶端的仰角为,悬崖的高为144.5米,斜坡的坡度(或坡比),则信号塔的高度约为( )(参考数据:,,)
A.23米 B.24米 C.24.5米 D.25米
6.如图,小明为了测量照母山上“览星塔”AB的高度,先从与塔底中心B在同一水平面上的点D出发,沿着坡度为1:0.75的斜坡DE行走10米至坡顶E处,再从E处沿水平方向继续前行若干米后至点F处,在F点测得塔顶A的仰角为63°,塔底C的俯角为45°,B与C的水平距离为4米(图中A、B、C、D、E、F在同一平面内,E、F和D、C、B分别在同一水平线上),根据小明的测量数据,计算出“览星塔”AB的高度约为(计算结果精确到0.1米,参考数据:sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)( )
A.17.8米 B.23.7米 C.31.5米 D.37.4米
7.如图所示,有一山坡在水平方向每前进100m就升高60m,那么山坡的坡度为( )
A. B. C. D.
8.如图,一棵松树AB挺立在斜坡CB的顶端,斜坡CB长为52米,坡度为i=12:5,小张从与点C相距60米的点D处向上爬12米到达观景台DE的顶端点E,在此测得松树顶端点A的仰角为39°,则松树的高度AB约为( )(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
A.16.8米 B.28.8米 C.40.8米 D.64.2米
9.西南大学附中初2020级小李同学想利用学过的知识测量一棵树的高度,假设树是竖直生长的,用图中线段AB表示,小李站在C点测得∠BCA=45°,小李从C点走4米到达了斜坡DE的底端D点,并测得∠CDE=150°,从D点上斜坡走了8米到达E点,测得∠AED=60°,B,C,D在同一水平线上,A、B、C、D、E在同一平面内,则大树AB的高度约为( )米.(结果精确到0.1米,参考数据:,)
A.24.3 B.24.4 C.20.3 D.20.4
10.如图,某航拍无人机从A点俯拍在坡比为3:4的斜坡上的景点C,此时的俯角为,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为.已知无人机与斜坡的坡底D的水平距离为400米,则斜坡的长度约为(精确到0.1米,参考数据:)( )
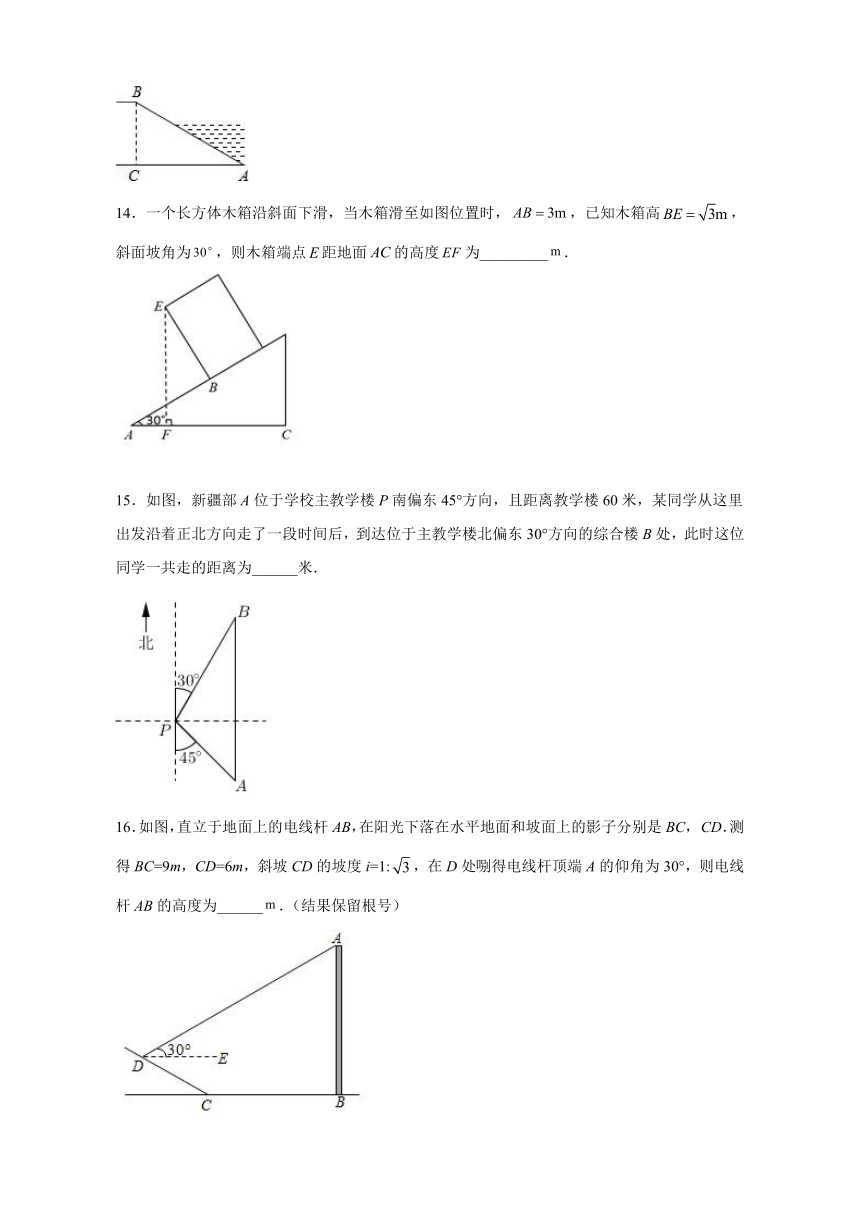
A.91.1米 B.91.3米 C.58.2米 D.58.4米
11.无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为的处测得试验田右侧出界处俯角为,无人机垂直下降至处,又测得试验田左侧边界处俯角为,则,之间的距离为(参考数据:,,,,结果保留整数)( )
A. B.
C. D.
12.如图,是梯子两梯腿张开的示意图,AB=AC,梯腿与地面夹角∠ACB=∠,当梯子顶端离地面高度AD=2.8m时,则梯子两梯脚之间的距离BC=( )m.
A. B. C. D.
二、填空题
13.如图,河坝横断面迎水坡AB的坡比为1:(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=4m,则坡面AB的长度是_____m.
14.一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,,已知木箱高,斜面坡角为,则木箱端点距地面的高度为_________.
15.如图,新疆部A位于学校主教学楼P南偏东45°方向,且距离教学楼60米,某同学从这里出发沿着正北方向走了一段时间后,到达位于主教学楼北偏东30°方向的综合楼B处,此时这位同学一共走的距离为______米.
16.如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC, CD.测得BC=9m,CD=6m,斜坡CD的坡度i=1:,在D处哵得电线杆顶端A的仰角为30°,则电线杆AB的高度为______.(结果保留根号)
17.一颗珍贵的百年老树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,做法如下:在地面上选取一点,测得,米,,则这棵树的高约为________米.(结果精确到0.1,参考数据:,,)
三、解答题
18.如图,在同一平面内,两条平行高速公路l1和l2间有一条“7”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB段垂直,长为30km,求两高速公路间的距离(结果保留根号).
19.如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=140°,BD=520m,∠D=50°,那么另一边开挖点E离D多远正好使A,C,E三点在一直线上(结果保留小数点后一位,cos50°=0.6428)?
20.避雷针是用来保护建筑物、高大树木等避免雷击的装置.如图,小陶同学要测量垂直于地面的大楼顶部避雷针的长度(,,三点共线),在水平地面点测得,,点与大楼底部点的距离,求避雷针的长度.(结果精确到.参考数据:,,,,,)
21.如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图.托板AB=120mm,支撑板CD=80mm,底座DE=90mm.托板AB与支撑板顶端C连接,CB=40mm,AB可绕点C转动,CD可绕点D转动.(结果保留小数点后一位)
(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;
(2)为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.(参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839;sin26.6°≈0.448,cos26.6°≈0.894,tan26.6°≈0.500,)
22.有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度,图2是这种升降熨烫台的平面示意图,和是两根相同长度的活动支撑杆,点O是它们的连接点,,,表示熨烫台的高度.
(1)如图2,若,.
①点O到的距离为__________,的长为__________(结果保留根号);
②若,则熨烫台的高度h=__________;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度h为时,两根支撑杆的夹角是74°(如图3).求该熨烫台支撑杆的长度.
(参考数据:,,,
参考答案
1.C
解:由题意得,∠B=α,
在Rt△ABC中,sinB,
则AB,
故选:C.
2.D
解:如图,RA⊥PQ于A,PQ=20(1+)海里,∠RQP=45°,∠RPA=30°,
设AR=x海里,
在Rt△RAQ中,RA=AQ=x,
在Rt△RPA中,PR=2x,PA=x,
∵PA+QA=PQ,
∴x+x=20(1+),解得x=20,
∴PR=2x=40.
答:船R到岛P的距离为40海里.
故选:D.
3.C
解:∵PA⊥PB,
∴∠APC=90°,
∵PC=50米,∠PCA=44°,
∴tan44°=,
∴小河宽PA=PCtan∠PCA=50 tan44°米.
故选:C.
4.C
解:过点O作OE⊥AC于点E,延长BD交OE于点F,
设DF=x,则BF=3+x,
∵tan65°=,
∴OF=xtan65°≈2.1x,
∵tan35°=,
∴OF=(3+x)tan35°≈0.7(3+x),
∴2.1x=0.7(3+x),
∴x=1.5,
∴OF=1.5×2.1=3.15,
∴OE=3.15+1.55=4.7米,
故选:C.
5.D
解:过E作EF∥CD交AC于F,作EG⊥CD交CD延长线于G,
则CD=78米,DE=78米,
在Rt△EGD中,,设EG=x米,GD=2.4x米,
根据勾股定理,即
解得x=30,2.4x=72,
∵EG⊥CD,AC⊥CD,EF∥CD,
∴EG⊥EF,AC⊥EF,
∴∠EGC=∠FCG=∠GEF=90°,
∴四边形EGCF为矩形,
∴CF=EG=30米,EF=GC=GD+CD=72+78=150米,
在Rt△EFA中,∠AEF=43°,
∴AF=EFtan43°≈150×0.93=139.5,
∴AB=AC-BC==AF+FC-BC=139.5+30-144.5=25米.
故选择D.
6.C
解:过F作FG⊥AB于G,过C作CH⊥FG于H,如图所示:
则PE=CH=BG,GH=BC=4,
∵斜坡DE的坡度为1:0.75,
∴==,
设PD=3x,则PE=4x,
在Rt△PDE中,由勾股定理得:DE==5x,
∴5x=10,
∴x=2,
∴CH=BG=PE=8,
∵∠CFH=45°,
∴△CFH是等腰直角三角形,
∴FH=CH=8,
∴FG=FH+GH=12,
在Rt△AFG中,tan∠AFG=,
∴AG=FG×tan63°≈12×1.96=23.52,
∴AB=AG+BG=23.52+8=31.5(米),
即“览星塔”AB的高度约为31.5米,
故选:C.
7.A
解:铅直高度为,水平宽度为,
山坡的坡度,
故选.
8.B
解:延长AB交DC的延长线于H,作EF⊥AH于F,则四边形EDHF为矩形,
∴FH=DE=12米,EF=DH,
∵斜坡CB的坡度为t=12:5,
∴设BH=12x,CH=5x,
由勾股定理得,(5x)2+(12x)2=522,
解得,x=4,
则BH=12x=48米,CH=5x=20米,
则EF=DH=DC+CH=60+20=80(米),
在Rt△AEF中,tan∠AEF=,
则AF=EF tan∠AEF≈80×0.81=64.8(米),
∴AB=AF+HF﹣BH=64.8+12﹣48=28.8(米),
故选:B.
9.B
解:过E作EG⊥AB于G,EF⊥BD于F,
则BG=EF,EG=BF,
∵∠CDE=150°,
∴∠EDF=30°,
∵DE=8,
∴EF=DE=4,DF=4,
∴CF=CD+DF=4+4,
∵∠ABC=90°,∠ACB=45°,
∴AB=BC,
∴GE=BF=AB+4+4,AG=AB-4,
∵∠AED=60°,∠GED=∠EDF=30°,
∴∠AEG=30°,
∴,
解得:AB=14+6≈24.4,
故选:B.
10.B
解:如图,过点C作于点P,于点Q,
由题意知,,
设,则,
∵,
∴,
即,解得,
∴,
∵,
∴,
∵斜坡的坡比为:,
∴设,则,
∴,
∴,
∴,
即斜坡的长度约91.3米.
故选B.
11.C
解:由题意得:OA⊥MN,∠N=43°,∠M=35°,OA=135m,AB=40m,
∴,
∴,,
∴;
故选C.
12.D
解:∵AB=AC,AD⊥BC,
∴BD=DC=BC,
在Rt△ADC中,tanC=,
∴DC==,
∴BC=2DC=,
故选:D.
13.
解:在Rt△ABC中,BC=4米,tanA=1:;
∴AC=BC÷tanA=,
,
故答案为:.
14.3
解:连接AE,在Rt△ABE中,已知AB=3m,BE=,
∴根据勾股定理得.
又∵,∴.
在Rt△AEF中,,
∴.
故答案为:3.
15..
解:过P作PC⊥AB于C,
∵新疆部A位于学校主教学楼P南偏东45°方向,
∴∠A=45°
∴∠CPA=90°-∠A=45°,
∴PC=AC,
设AC=PC=x,
∵PA=60米
∴AC=PC=PAcos45°=60,
∵综合楼B处在教学楼北偏东30°方向,
∴∠B=30°,
∴PB=2PC=,
在Rt△BCP中,BC=PBcos30°,
∴AB=BC+AC米.
故答案为:.
16.6+3
解:如图,延长AD交BC的延长线于F,作DG⊥BF于G,
∵∠ADE=30°,
∴∠AFB=30°,
∵CD=6m,斜坡CD的坡度i=1:,
∴tan∠DCG=,
∴∠DCG=30°,
∴DG=3m,CG=3m,
∴∠DFC=∠DCF=30°,
∴DF=DC,
∵DG⊥BF,
∴FG=CG=3(m),
∴FC=6m,
∴FB=FC+BC=(6+9)m,
∴AB=BF×tan∠AFB=(6+9)×=(6+3)m.
故答案为:6+3.
17.
解:如图,过点B作BH⊥AC于点H,
设 米,
∵,∠BHC=90°,
∴ ,
∵,
∴∠ABH=45°,
∴∠ABH=∠BAC,
∴AH=BH=x,
∵米,
∴ ,解得: ,
∴AH=BH=12
∴ (米).
故答案为: .
18.两高速公路间的距离为(10+15)千米
解:如图,过B作MN⊥l1于M,交l2于N,
∵l1l2,
∴MN⊥l2,
∴∠AMB=∠BNC=90°,
∴在中,,
∵∠BAM=30°,AB=20,
∴,
∴BM=20×=10(千米),
∵BC⊥AB,
∴∠ABC=90°,
∴∠CBN=90°﹣60°=30°,
∵在中,,
又∵BC=30,
∴,
∴BN=30×=15,
∴AB和CD之间的距离=BM+BN=10+15(千米),
答:两高速公路间的距离为(10+15)千米.
19.334.3米
解:∵∠ABD=140°,
∴∠DBE=180°﹣140°=40°,
又∵∠D=50°,
∴∠E=180°﹣∠DBE﹣∠D
=180°﹣40°﹣50°
=90°,
∴RtBED中, cosD=,
∴cos50°==0.6428,
解得:DE=334.3m.
答:另一边开挖点E离D334.3米正好使A,C,E三点在一直线上.
20.
解:∵,
∴,
∵,,
∴,即,
解得:m,
∵,
∴,即,
解得:m,
∴m .
21.(1);(2)33.4°
解:(1)如图2,作AM⊥DE,交ED的延长线于点M,作CF⊥AM于F,作CN⊥DE于N
得矩形CFMN,Rt△ACF,Rt△CDN,∠AFC=∠CNM=∠FCN=90°
由题意,可知AB=120,CB=40,CD=80,∠DCB=80°,∠CDE=60°,
∴AC=80,
在Rt△CDN中,CN=CD sin∠CDE==FM,
∠DCN=90°﹣60°=30°,
又∵∠DCB=80°, ∴∠BCN=50°,
∴∠ACF=180°﹣90°﹣50°=40°,
在Rt△AFC中,AF=AC sin40°≈80×0.643≈51.44,
∴AM=AF+FM≈51.44+≈120.7,
答:点A到直线DE的距离约为120.7mm
(2)旋转后,如图3所示,根据题意可知∠DCB=80°+10°=90°
在Rt△BCD中,CD=80,BC=40,
∴tan∠D,
∴∠D≈26.6°,
因此旋转的角度为:60°-26.6°≈33.4°,
答:CD旋转的角度约为33.4°.
22.(1)①40,80;②50;(2)支撑杆AB长160cm.
解:(1)①如图2,过点O作OE⊥AC,垂足为E,
∵AO=CO=80cm,
∴∠AOE=∠AOC=×120°=60°,AC=2AE.
在Rt△AEO中,OE=OA=40(cm),
AE=AO sin∠AOE=80×=40(cm),
∴AC=2AE=80.
答:AC的长为80cm;
②延长EO交BD于F,
∵DB∥AC,
∴∠BFO=90°,∠FBO=30°,
∵OB=20cm,
∴OF=OB=×20=10(cm),
∴h=OF+OE=10+40=50,
故答案为:40,80,50;
(2)如图,过点B作BF⊥AC,垂足为F,则BF=128cm,
∵AO=CO,∠AOC=74°,
∴∠OAC=∠OCA==53°,
在Rt△ABF中,AB===160(cm),
答:支撑杆AB长160cm.
一、单选题
1.如图,飞机于空中A处测得目标B处的俯角为α,此时飞机的高度AC为a米,则AB的距离为( )米
A.atanα B. C. D.
2.如图,岛P位于岛Q的正西方,P、Q两岛间的距离为海里,由岛P、Q分别测得船R位于南偏东和南偏西方向上,则船R到岛P的距离为( )
A.海里 B.海里 C.20海里 D.40海里
3.如图要测量小河两岸相对的两点P、A的距离,可以在小河边取的垂线上的一点C,测得米,,则小河宽为( )米
A. B. C. D.
4.小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高为1.55米,她先站在处看路灯顶端的仰角为35°,再往前走3米站在处,看路灯顶端的仰角为65°,则路灯顶端到地而的距离为(已知,,,,,)( )
A.3.2米 B.3.9米 C.4.7米 D.5.4米
5.重庆移动为了提升网络信号,修建了多个5G信号塔,如图,垂直于水平面的信号塔建在垂直于水平面的悬崖边点处.某测量员从山脚点出发沿水平方向前行78米 到点(点,,在同一直线上),再沿斜坡方向前行78米到点(点,,,,在同一平面内),在点处测得信号塔顶端的仰角为,悬崖的高为144.5米,斜坡的坡度(或坡比),则信号塔的高度约为( )(参考数据:,,)
A.23米 B.24米 C.24.5米 D.25米
6.如图,小明为了测量照母山上“览星塔”AB的高度,先从与塔底中心B在同一水平面上的点D出发,沿着坡度为1:0.75的斜坡DE行走10米至坡顶E处,再从E处沿水平方向继续前行若干米后至点F处,在F点测得塔顶A的仰角为63°,塔底C的俯角为45°,B与C的水平距离为4米(图中A、B、C、D、E、F在同一平面内,E、F和D、C、B分别在同一水平线上),根据小明的测量数据,计算出“览星塔”AB的高度约为(计算结果精确到0.1米,参考数据:sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)( )
A.17.8米 B.23.7米 C.31.5米 D.37.4米
7.如图所示,有一山坡在水平方向每前进100m就升高60m,那么山坡的坡度为( )
A. B. C. D.
8.如图,一棵松树AB挺立在斜坡CB的顶端,斜坡CB长为52米,坡度为i=12:5,小张从与点C相距60米的点D处向上爬12米到达观景台DE的顶端点E,在此测得松树顶端点A的仰角为39°,则松树的高度AB约为( )(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
A.16.8米 B.28.8米 C.40.8米 D.64.2米
9.西南大学附中初2020级小李同学想利用学过的知识测量一棵树的高度,假设树是竖直生长的,用图中线段AB表示,小李站在C点测得∠BCA=45°,小李从C点走4米到达了斜坡DE的底端D点,并测得∠CDE=150°,从D点上斜坡走了8米到达E点,测得∠AED=60°,B,C,D在同一水平线上,A、B、C、D、E在同一平面内,则大树AB的高度约为( )米.(结果精确到0.1米,参考数据:,)
A.24.3 B.24.4 C.20.3 D.20.4
10.如图,某航拍无人机从A点俯拍在坡比为3:4的斜坡上的景点C,此时的俯角为,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为.已知无人机与斜坡的坡底D的水平距离为400米,则斜坡的长度约为(精确到0.1米,参考数据:)( )
A.91.1米 B.91.3米 C.58.2米 D.58.4米
11.无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为的处测得试验田右侧出界处俯角为,无人机垂直下降至处,又测得试验田左侧边界处俯角为,则,之间的距离为(参考数据:,,,,结果保留整数)( )
A. B.
C. D.
12.如图,是梯子两梯腿张开的示意图,AB=AC,梯腿与地面夹角∠ACB=∠,当梯子顶端离地面高度AD=2.8m时,则梯子两梯脚之间的距离BC=( )m.
A. B. C. D.
二、填空题
13.如图,河坝横断面迎水坡AB的坡比为1:(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=4m,则坡面AB的长度是_____m.
14.一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,,已知木箱高,斜面坡角为,则木箱端点距地面的高度为_________.
15.如图,新疆部A位于学校主教学楼P南偏东45°方向,且距离教学楼60米,某同学从这里出发沿着正北方向走了一段时间后,到达位于主教学楼北偏东30°方向的综合楼B处,此时这位同学一共走的距离为______米.
16.如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC, CD.测得BC=9m,CD=6m,斜坡CD的坡度i=1:,在D处哵得电线杆顶端A的仰角为30°,则电线杆AB的高度为______.(结果保留根号)
17.一颗珍贵的百年老树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,做法如下:在地面上选取一点,测得,米,,则这棵树的高约为________米.(结果精确到0.1,参考数据:,,)
三、解答题
18.如图,在同一平面内,两条平行高速公路l1和l2间有一条“7”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB段垂直,长为30km,求两高速公路间的距离(结果保留根号).
19.如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=140°,BD=520m,∠D=50°,那么另一边开挖点E离D多远正好使A,C,E三点在一直线上(结果保留小数点后一位,cos50°=0.6428)?
20.避雷针是用来保护建筑物、高大树木等避免雷击的装置.如图,小陶同学要测量垂直于地面的大楼顶部避雷针的长度(,,三点共线),在水平地面点测得,,点与大楼底部点的距离,求避雷针的长度.(结果精确到.参考数据:,,,,,)
21.如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图.托板AB=120mm,支撑板CD=80mm,底座DE=90mm.托板AB与支撑板顶端C连接,CB=40mm,AB可绕点C转动,CD可绕点D转动.(结果保留小数点后一位)
(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;
(2)为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.(参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839;sin26.6°≈0.448,cos26.6°≈0.894,tan26.6°≈0.500,)
22.有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度,图2是这种升降熨烫台的平面示意图,和是两根相同长度的活动支撑杆,点O是它们的连接点,,,表示熨烫台的高度.
(1)如图2,若,.
①点O到的距离为__________,的长为__________(结果保留根号);
②若,则熨烫台的高度h=__________;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度h为时,两根支撑杆的夹角是74°(如图3).求该熨烫台支撑杆的长度.
(参考数据:,,,
参考答案
1.C
解:由题意得,∠B=α,
在Rt△ABC中,sinB,
则AB,
故选:C.
2.D
解:如图,RA⊥PQ于A,PQ=20(1+)海里,∠RQP=45°,∠RPA=30°,
设AR=x海里,
在Rt△RAQ中,RA=AQ=x,
在Rt△RPA中,PR=2x,PA=x,
∵PA+QA=PQ,
∴x+x=20(1+),解得x=20,
∴PR=2x=40.
答:船R到岛P的距离为40海里.
故选:D.
3.C
解:∵PA⊥PB,
∴∠APC=90°,
∵PC=50米,∠PCA=44°,
∴tan44°=,
∴小河宽PA=PCtan∠PCA=50 tan44°米.
故选:C.
4.C
解:过点O作OE⊥AC于点E,延长BD交OE于点F,
设DF=x,则BF=3+x,
∵tan65°=,
∴OF=xtan65°≈2.1x,
∵tan35°=,
∴OF=(3+x)tan35°≈0.7(3+x),
∴2.1x=0.7(3+x),
∴x=1.5,
∴OF=1.5×2.1=3.15,
∴OE=3.15+1.55=4.7米,
故选:C.
5.D
解:过E作EF∥CD交AC于F,作EG⊥CD交CD延长线于G,
则CD=78米,DE=78米,
在Rt△EGD中,,设EG=x米,GD=2.4x米,
根据勾股定理,即
解得x=30,2.4x=72,
∵EG⊥CD,AC⊥CD,EF∥CD,
∴EG⊥EF,AC⊥EF,
∴∠EGC=∠FCG=∠GEF=90°,
∴四边形EGCF为矩形,
∴CF=EG=30米,EF=GC=GD+CD=72+78=150米,
在Rt△EFA中,∠AEF=43°,
∴AF=EFtan43°≈150×0.93=139.5,
∴AB=AC-BC==AF+FC-BC=139.5+30-144.5=25米.
故选择D.
6.C
解:过F作FG⊥AB于G,过C作CH⊥FG于H,如图所示:
则PE=CH=BG,GH=BC=4,
∵斜坡DE的坡度为1:0.75,
∴==,
设PD=3x,则PE=4x,
在Rt△PDE中,由勾股定理得:DE==5x,
∴5x=10,
∴x=2,
∴CH=BG=PE=8,
∵∠CFH=45°,
∴△CFH是等腰直角三角形,
∴FH=CH=8,
∴FG=FH+GH=12,
在Rt△AFG中,tan∠AFG=,
∴AG=FG×tan63°≈12×1.96=23.52,
∴AB=AG+BG=23.52+8=31.5(米),
即“览星塔”AB的高度约为31.5米,
故选:C.
7.A
解:铅直高度为,水平宽度为,
山坡的坡度,
故选.
8.B
解:延长AB交DC的延长线于H,作EF⊥AH于F,则四边形EDHF为矩形,
∴FH=DE=12米,EF=DH,
∵斜坡CB的坡度为t=12:5,
∴设BH=12x,CH=5x,
由勾股定理得,(5x)2+(12x)2=522,
解得,x=4,
则BH=12x=48米,CH=5x=20米,
则EF=DH=DC+CH=60+20=80(米),
在Rt△AEF中,tan∠AEF=,
则AF=EF tan∠AEF≈80×0.81=64.8(米),
∴AB=AF+HF﹣BH=64.8+12﹣48=28.8(米),
故选:B.
9.B
解:过E作EG⊥AB于G,EF⊥BD于F,
则BG=EF,EG=BF,
∵∠CDE=150°,
∴∠EDF=30°,
∵DE=8,
∴EF=DE=4,DF=4,
∴CF=CD+DF=4+4,
∵∠ABC=90°,∠ACB=45°,
∴AB=BC,
∴GE=BF=AB+4+4,AG=AB-4,
∵∠AED=60°,∠GED=∠EDF=30°,
∴∠AEG=30°,
∴,
解得:AB=14+6≈24.4,
故选:B.
10.B
解:如图,过点C作于点P,于点Q,
由题意知,,
设,则,
∵,
∴,
即,解得,
∴,
∵,
∴,
∵斜坡的坡比为:,
∴设,则,
∴,
∴,
∴,
即斜坡的长度约91.3米.
故选B.
11.C
解:由题意得:OA⊥MN,∠N=43°,∠M=35°,OA=135m,AB=40m,
∴,
∴,,
∴;
故选C.
12.D
解:∵AB=AC,AD⊥BC,
∴BD=DC=BC,
在Rt△ADC中,tanC=,
∴DC==,
∴BC=2DC=,
故选:D.
13.
解:在Rt△ABC中,BC=4米,tanA=1:;
∴AC=BC÷tanA=,
,
故答案为:.
14.3
解:连接AE,在Rt△ABE中,已知AB=3m,BE=,
∴根据勾股定理得.
又∵,∴.
在Rt△AEF中,,
∴.
故答案为:3.
15..
解:过P作PC⊥AB于C,
∵新疆部A位于学校主教学楼P南偏东45°方向,
∴∠A=45°
∴∠CPA=90°-∠A=45°,
∴PC=AC,
设AC=PC=x,
∵PA=60米
∴AC=PC=PAcos45°=60,
∵综合楼B处在教学楼北偏东30°方向,
∴∠B=30°,
∴PB=2PC=,
在Rt△BCP中,BC=PBcos30°,
∴AB=BC+AC米.
故答案为:.
16.6+3
解:如图,延长AD交BC的延长线于F,作DG⊥BF于G,
∵∠ADE=30°,
∴∠AFB=30°,
∵CD=6m,斜坡CD的坡度i=1:,
∴tan∠DCG=,
∴∠DCG=30°,
∴DG=3m,CG=3m,
∴∠DFC=∠DCF=30°,
∴DF=DC,
∵DG⊥BF,
∴FG=CG=3(m),
∴FC=6m,
∴FB=FC+BC=(6+9)m,
∴AB=BF×tan∠AFB=(6+9)×=(6+3)m.
故答案为:6+3.
17.
解:如图,过点B作BH⊥AC于点H,
设 米,
∵,∠BHC=90°,
∴ ,
∵,
∴∠ABH=45°,
∴∠ABH=∠BAC,
∴AH=BH=x,
∵米,
∴ ,解得: ,
∴AH=BH=12
∴ (米).
故答案为: .
18.两高速公路间的距离为(10+15)千米
解:如图,过B作MN⊥l1于M,交l2于N,
∵l1l2,
∴MN⊥l2,
∴∠AMB=∠BNC=90°,
∴在中,,
∵∠BAM=30°,AB=20,
∴,
∴BM=20×=10(千米),
∵BC⊥AB,
∴∠ABC=90°,
∴∠CBN=90°﹣60°=30°,
∵在中,,
又∵BC=30,
∴,
∴BN=30×=15,
∴AB和CD之间的距离=BM+BN=10+15(千米),
答:两高速公路间的距离为(10+15)千米.
19.334.3米
解:∵∠ABD=140°,
∴∠DBE=180°﹣140°=40°,
又∵∠D=50°,
∴∠E=180°﹣∠DBE﹣∠D
=180°﹣40°﹣50°
=90°,
∴RtBED中, cosD=,
∴cos50°==0.6428,
解得:DE=334.3m.
答:另一边开挖点E离D334.3米正好使A,C,E三点在一直线上.
20.
解:∵,
∴,
∵,,
∴,即,
解得:m,
∵,
∴,即,
解得:m,
∴m .
21.(1);(2)33.4°
解:(1)如图2,作AM⊥DE,交ED的延长线于点M,作CF⊥AM于F,作CN⊥DE于N
得矩形CFMN,Rt△ACF,Rt△CDN,∠AFC=∠CNM=∠FCN=90°
由题意,可知AB=120,CB=40,CD=80,∠DCB=80°,∠CDE=60°,
∴AC=80,
在Rt△CDN中,CN=CD sin∠CDE==FM,
∠DCN=90°﹣60°=30°,
又∵∠DCB=80°, ∴∠BCN=50°,
∴∠ACF=180°﹣90°﹣50°=40°,
在Rt△AFC中,AF=AC sin40°≈80×0.643≈51.44,
∴AM=AF+FM≈51.44+≈120.7,
答:点A到直线DE的距离约为120.7mm
(2)旋转后,如图3所示,根据题意可知∠DCB=80°+10°=90°
在Rt△BCD中,CD=80,BC=40,
∴tan∠D,
∴∠D≈26.6°,
因此旋转的角度为:60°-26.6°≈33.4°,
答:CD旋转的角度约为33.4°.
22.(1)①40,80;②50;(2)支撑杆AB长160cm.
解:(1)①如图2,过点O作OE⊥AC,垂足为E,
∵AO=CO=80cm,
∴∠AOE=∠AOC=×120°=60°,AC=2AE.
在Rt△AEO中,OE=OA=40(cm),
AE=AO sin∠AOE=80×=40(cm),
∴AC=2AE=80.
答:AC的长为80cm;
②延长EO交BD于F,
∵DB∥AC,
∴∠BFO=90°,∠FBO=30°,
∵OB=20cm,
∴OF=OB=×20=10(cm),
∴h=OF+OE=10+40=50,
故答案为:40,80,50;
(2)如图,过点B作BF⊥AC,垂足为F,则BF=128cm,
∵AO=CO,∠AOC=74°,
∴∠OAC=∠OCA==53°,
在Rt△ABF中,AB===160(cm),
答:支撑杆AB长160cm.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
