25.4相似三角形的判定 解答题专题训练 2021-2022学年冀教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 25.4相似三角形的判定 解答题专题训练 2021-2022学年冀教版九年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 492.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 00:00:00 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学上册《25.4相似三角形的判定》解答题专题训练(附答案)
1.如图,在△ABC中,∠B=90°,AB=4,BC=2,以AC为边作△ACE,∠ACE=90°,AC=CE,延长BC至点D,使CD=5,连接DE.求证:△ABC∽△CED.
2.如图,在△ABC中,D、E分别是边AC、BC的中点,F是BC延长线上一点,∠F=∠B.
(1)若AB=10,求FD的长;
(2)若AC=BC,求证:△CDE∽△DFE.
3.如图,在平面直角坐标系中,已知OA=6厘米,OB=8厘米.点P从点B开始沿BA边向终点A以1厘米/秒的速度移动;点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发,运动时间为t(s).
(1)当t为何值时,△APQ与△AOB相似?
(2)当t为何值时,△APQ的面积为8cm2?
4.如图,点B、D、E在一条直线上,BE交AC于点F,=,且∠BAD=∠CAE.
(1)求证:△ABC∽△ADE;
(2)求证:△AEF∽△BCF.
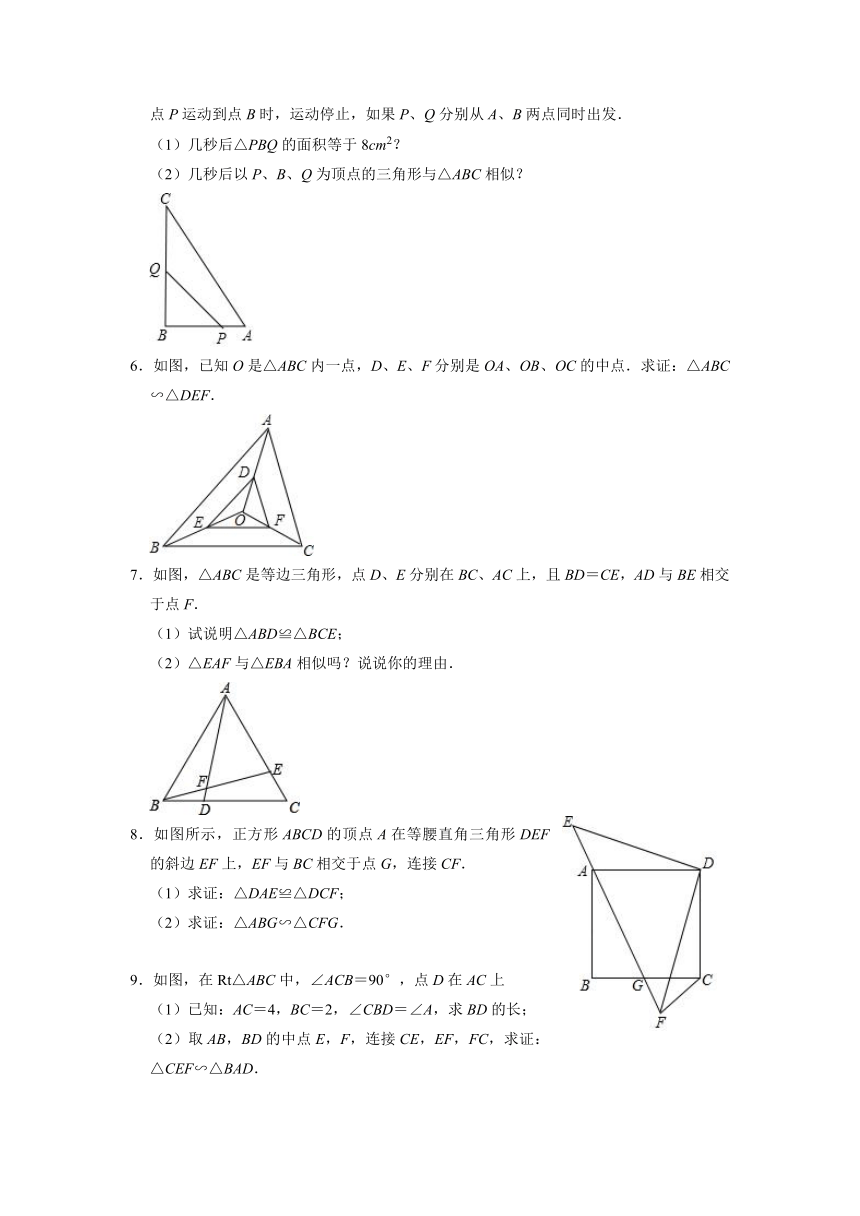
5.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边以1cm/s的速度向点B运动:点Q从点B开始,沿BC边以2cm/s的速度向点C运动,当点P运动到点B时,运动停止,如果P、Q分别从A、B两点同时出发.
(1)几秒后△PBQ的面积等于8cm2?
(2)几秒后以P、B、Q为顶点的三角形与△ABC相似?
6.如图,已知O是△ABC内一点,D、E、F分别是OA、OB、OC的中点.求证:△ABC∽△DEF.
7.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
8.如图所示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
(1)求证:△DAE≌△DCF;
(2)求证:△ABG∽△CFG.
9.如图,在Rt△ABC中,∠ACB=90°,点D在AC上
(1)已知:AC=4,BC=2,∠CBD=∠A,求BD的长;
(2)取AB,BD的中点E,F,连接CE,EF,FC,求证:△CEF∽△BAD.
10.如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.
请解答下列问题:
(1)当t为何值时,△CEF是等腰直角三角形?
(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?
11.如图, ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:△BDE是直角三角形;
(2)如果OE⊥CD,试判断△BDE与△DCE是否相似,并说明理由.
12.如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且==.
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)试判断△ABE与△ACD是否相似?并说明理由.
13.在△ABC和△A′B′C′中,已知:AB=6cm,BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm.试证明△ABC与△A′B′C′相似.
14.如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.写出图中三对相似三角形,并证明其中的一对.
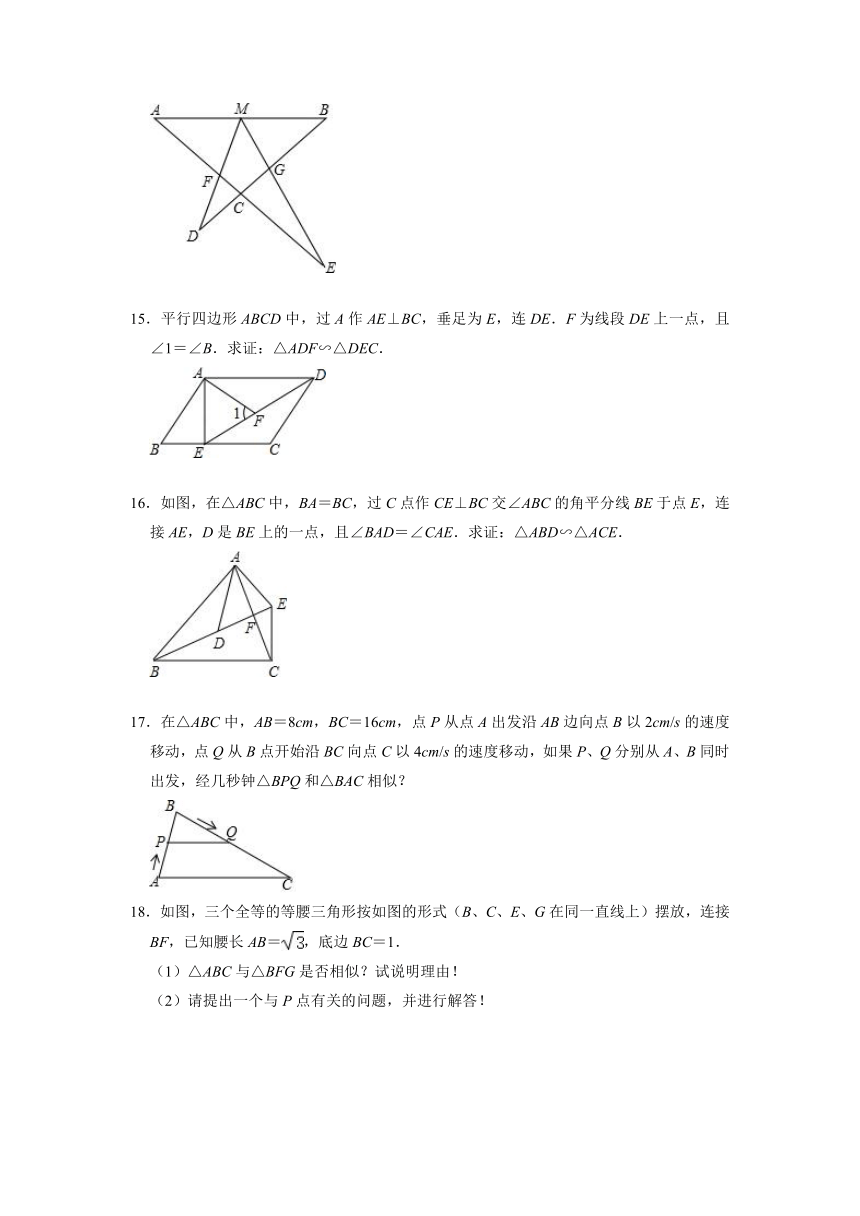
15.平行四边形ABCD中,过A作AE⊥BC,垂足为E,连DE.F为线段DE上一点,且∠1=∠B.求证:△ADF∽△DEC.
16.如图,在△ABC中,BA=BC,过C点作CE⊥BC交∠ABC的角平分线BE于点E,连接AE,D是BE上的一点,且∠BAD=∠CAE.求证:△ABD∽△ACE.
17.在△ABC中,AB=8cm,BC=16cm,点P从点A出发沿AB边向点B以2cm/s的速度移动,点Q从B点开始沿BC向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,经几秒钟△BPQ和△BAC相似?
18.如图,三个全等的等腰三角形按如图的形式(B、C、E、G在同一直线上)摆放,连接BF,已知腰长AB=,底边BC=1.
(1)△ABC与△BFG是否相似?试说明理由!
(2)请提出一个与P点有关的问题,并进行解答!
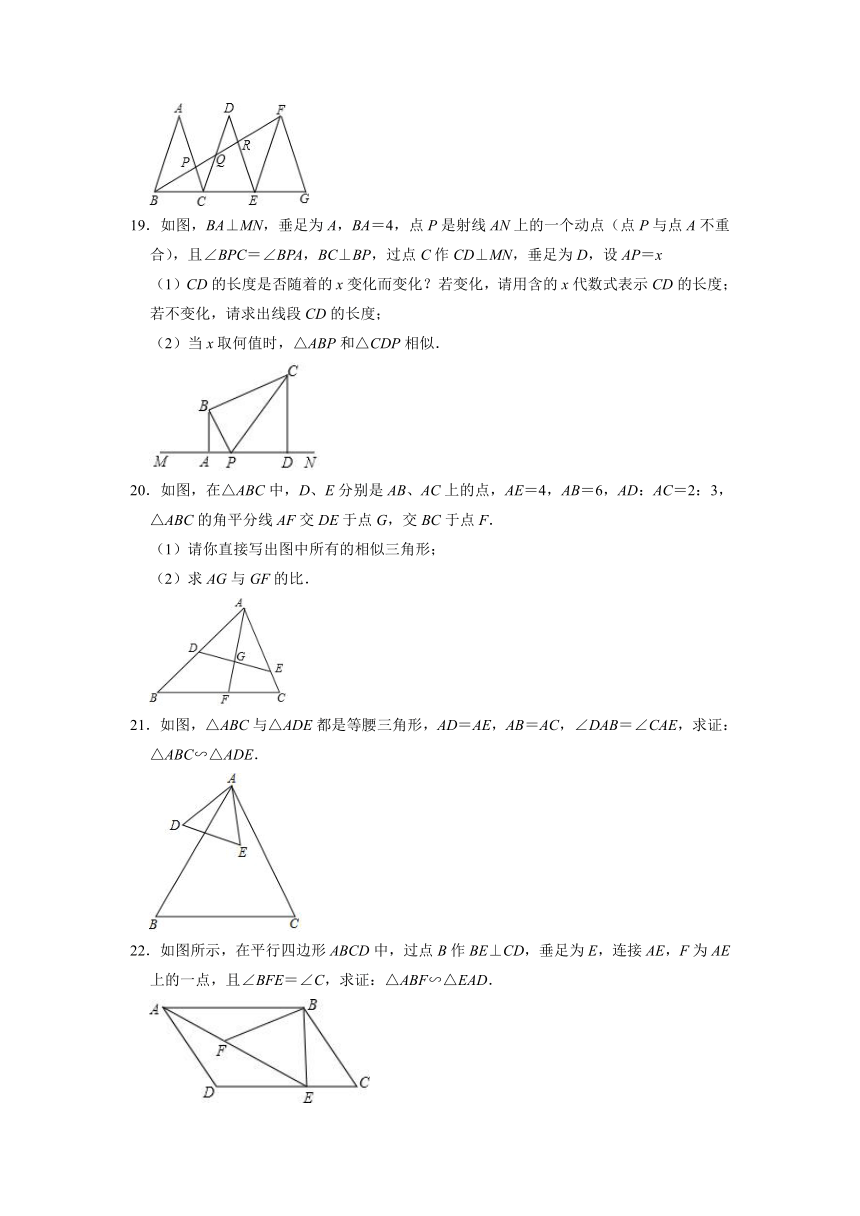
19.如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),且∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x
(1)CD的长度是否随着的x变化而变化?若变化,请用含的x代数式表示CD的长度;若不变化,请求出线段CD的长度;
(2)当x取何值时,△ABP和△CDP相似.
20.如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.
(1)请你直接写出图中所有的相似三角形;
(2)求AG与GF的比.
21.如图,△ABC与△ADE都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE,求证:△ABC∽△ADE.
22.如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C,求证:△ABF∽△EAD.
23.如图,已知△ABC中,AB=AC=15,BC=10,动点P沿CA方向从点C向点A运动,同时,动点Q沿CB方向从点C向点B运动,速度都为每秒1个单位长度,P、Q中任意一点到达终点时,另一点也随之停止运动.过点P作PD∥BC,交AB边于点D,连接DQ.设P、Q的运动时间为t.
(1)直接写出BD的长;(用含t的代数式表示)
(2)求当t为何值时,△ADP与△BDQ相似.
24.如图,△ABC中,∠C=90°,AC=6,BC=8,点D是AB的中点,点E在DC的延长线上,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
(1)求证:AC=CG;
(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.
25.如图,等腰△ABC中,BA=BC,AO=3CO=6.动点F在BA上以每分钟5个单位长度的速度从B点出发向A点移动,过F作FE∥BC交AC边于E点,连接FO、EO.
(1)求A、B两点的坐标;
(2)证明:当△EFO面积最大时,△EFO∽△CBA.
26.如图,在△ABC中,AD、BE分别是BC、AC边上的高.求证:△DCE∽△ACB.
27.甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”.
甲同学的解答得到了老师的好评.
乙同学的解答是这样的:“与△ABC相似的三角形只有△AFD,证明如下:
∵DF∥CB,
∴△AFD∽△ABC.”
乙同学的解答正确吗?若不正确,请你改正.
28.如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连接AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.
29.如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长与CE交于点E.求证:△ABD∽△CED.
30.在△ABC中,∠BAC=90°,AB=AC,点D是BC边上一点,过点D作∠ADE=45°,DE交AC于点E,求证:△ABD∽△DCE.
参考答案
1.证明:∵∠B=90°,AB=4,BC=2,
∴AC==2,
∵CE=AC,
∴CE=2,
∵CD=5,
∵==,=,
∴=,
∵∠B=90°,∠ACE=90°,
∴∠BAC+∠BCA=90°,∠BCA+∠DCE=90°.
∴∠BAC=∠DCE.
∴△ABC∽△CED.
2.解:(1)∵D、E分别是AC、BC的中点,
∴DE∥AB,DE=AB=5,
∵DE∥AB,
∴∠DEC=∠B,而∠F=∠B,
∴∠DEC=∠F,
∴DF=DE=5;
(2)∵AC=BC,
∴∠A=∠B,
∵∠CDE=∠A,∠CED=∠B,
∴∠CDE=∠B,
∵∠B=∠F,
∴∠CDE=∠F,
∵∠CED=∠DEF,
∴△CDE∽△DFE.
3.解:(1)∵点A(0,6),B(8,0),
∴AO=6,BO=8,
∴AB===10,
∵点P的速度是每秒1个单位,点Q的速度是每秒1个单位,
∴AQ=t,AP=10﹣t,
①∠APQ是直角时,△APQ∽△AOB,
∴,
即,
解得t=>6,舍去;
②∠AQP是直角时,△AQP∽△AOB,
∴,
即,
解得t=,
综上所述,t=秒时,△APQ与△AOB相似;
(2)如图,过点P作PC⊥OA于点C,
则PC=AP sin∠OAB=(10﹣t)×=(10﹣t),
△APQ的面积=×t×(10﹣t)=8,
整理,得:t2﹣10t+20=0,
解得:t=5+>6(舍去),或t=5﹣;
故当t=5﹣s时,△APQ的面积为8cm2.
4.(1)∵∠BAD=∠CAE
∴∠BAD+∠CAD=∠CAE+∠CAD
即∠BAC=∠DAE
在△ABC和△ADE中
=,∠BAC=∠DAE,
∴△ABC∽△ADE;
(2)∵△ABC∽△ADE,
∴∠C=∠E、
在△AEF和△BFC中,∠C=∠E,∠AFE=∠BFC,
∴△AEF∽△BCF.
5.解:(1)设t秒后△PBQ的面积等于8cm,此时,AP=t,BP=6﹣t,BQ=2t,
∵S△PBQ=BP BQ,即(6﹣t)×2t=8,即t2﹣6t+8=0,解得t1=2,t2=4.
∴2秒或4秒后,△PBQ的面积等于8cm2;
(2)设x秒后以P、B、Q为顶点的三角形与△ABC相似,此时,AP=x,BP=6﹣x,BQ=2x,
①若△BPQ∽△BAC,则=,即=,解得x=3;
②若△BPQ∽△BCA,则=,即=,解得x=1.2.
综上所述,1.2秒或3秒后,以P、B、Q为顶点的三角形与△ABC相似.
6.证明:∵D、E、F分别是OA、OB、OC的中点,
∴DE=AB,EF=BC,DF=AC,
即==,
∴△ABC∽△DEF.
7.(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)答:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC﹣∠BAD=∠CBA﹣∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
8.证明:(1)∵正方形ABCD,等腰直角三角形EDF,
∴∠ADC=∠EDF=90°,AD=CD,DE=DF,
∴∠ADE+∠ADF=∠ADF+∠CDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF;
(2)延长BA到M,交ED于点M,
∵△ADE≌△CDF,
∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,
∵∠MAD=∠BCD=90°,
∴∠EAM=∠BCF,
∵∠EAM=∠BAG,
∴∠BAG=∠BCF,
∵∠AGB=∠CGF,
∴△ABG∽△CFG.
9.(1)解:∵∠CBD=∠A,∠BCD=∠ACB,
∴△CBD∽△CAB,
∴=,即=,
∴CD=1,
∴BD==.
(2)证明:∵E、F分别是Rt△ABC、Rt△BCD斜边上的中点,
∴CF=BD,CE=AB.
又∵E、F分别为是AB、BD的中点,
∴EF=AD,
∴===,
∴△CEF∽△BAD.
10.解:(1)当CE=CF时,△CEF是等腰三角形,
∴4t=12﹣2t,
∴t=2.
(2)①当=时,△ECF∽△ADC,
∴=,
∴t=3.
②当=时,△FCE∽△ADC,
∴=,
∴t=,
综上所述,当t=s或3s时,以点E,C,F为顶点的三角形与△ACD相似.
11.(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵OE=OB,
∴OE=OD,
∴∠OBE=∠OEB,∠ODE=∠OED,
∵∠OBE+∠OEB+∠ODE+∠OED=180°,
∴∠BED=∠OEB+∠OED=90°,
∴DE⊥BE,即△BDE是直角三角形;
(2)解:△BDE与△DCE相似.
∵OE⊥CD,
∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵∠OBE=∠OEB,
∴∠DBE=∠CDE,
∵∠BED=∠DEC=90°,
∴△BDE∽△DCE.
12.解:(1)∠BAE与∠CAD相等.
理由:∵==,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAE=∠CAD;
(2)△ABE与△ACD相似.
∵=,
∴=.
在△ABE与△ACD中,
∵=,∠BAE=∠CAD,
∴△ABE∽△ACD.
13.证明:∵AB=6cm,BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm,
∴==,==,==,
∴==,
∴△ABC∽△A′B′C′.
14.解:△AME∽△MFE,△BMD∽△MGD,△AMF∽△BGM,
①∵∠AMD=∠B+∠D,∠BGM=∠DMG+∠D
又∠B=∠A=∠DME=α
∴∠AMF=∠BGM,
∴△AMF∽△BGM;
②∵∠EAM=∠EMF、∠AEM=∠MEF,
∴△EMF∽△EAM;
③∵∠DBM=∠DMG,∠BDM=∠MDG,
∴△DMG∽△DBM.
15.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠DEC,∠C+∠B=180°.
∵∠1=∠B,∠1+∠AFD=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC.
16.解:∵BA=BC,BE平分∠ABC,
∴∠ABE=∠CBE,BE⊥AC(等腰三角形三线合一的性质),
∴∠CBE+∠ACB=90°,
又∵CE⊥BC,
∴∠ACE+∠ACB=90°,
∴∠CBE=∠ACE,
∴∠ABE=∠ACE,
∵∠BAD=∠CAE,
∴△ABD∽△ACE.
17.解:设经t秒钟△BPQ和△BAC相似,
当△BPQ∽△BAC时,=,
即=,
解得,t=2,
当△BPQ∽△BCA时,=,
即=,
解得,t=,
答:经2秒或秒钟△BPQ和△BAC相似.
18.解:
(1)相似,理由如下:
∵△ABC≌△DCE≌△FEG
∴BC=CE=EG=1,
∴BG=2BC=3,FG=AB=
∴==,=,即=,
又∠ACB=∠FGB,
∴△ABC∽△BFG;
(2)A层问题(较浅显的,仅用到了1个知识点).
例如:①求证:∠PCB=∠REB.(或问∠PCB与∠REB是否相等)等;
②求证:PC∥RE,(或问线段PC与RE是否平行)等.
B层问题(有一定思考的,用到了2~3个知识点).
例如:①求证:∠BPC=∠BFG等,求证:BP=PR等;
②求证:△ABP∽△CQP等,求证:△BPC∽△BRE等;
③求证:△ABP∽△DQR等;④求BP:PF的值等.
A层解答举例:求证:PC∥RE
证明:△ABC≌△DCE
∴∠PCB=∠REB
∴PC∥RE
B层解答举例:求证:BP=PR
证明:∠ACB=∠REB,
∴AC∥DE.
又BC=CE,∴BP=PR.
19.解:(1)CD的长度不变化.
理由如下:
如图1,延长CB和PA,记交点为点Q.
∵∠BPC=∠BPA,BC⊥BP,
∴QB=BC(等腰三角形“三合一”的性质).
∵BA⊥MN,CD⊥MN,
∴AB∥CD,
∴△QAB∽△QDC,
∴==,
∴CD=2AB=2×4=8,
即CD=8;
(2)当△BAP∽△CDP时,
∵∠BPC=∠BPA,∠CPD=∠BPA,
∴∠BPA=∠BPC=∠CPD=60°,
∴AP===,
即x=;
如图2,当△BAP∽△PDC时,
∵∠CPB=∠BPA,∠PCD=∠BPA,
∴3∠BPA=90°,
∴∠BPA=30°,
∴AP===4,
即x=4;
即当x=或4时,△ABP和△CDP相似.
20.解:(1)△ADG∽△ACF,△AGE∽△AFB,△ADE∽△ACB;
(2)∵==,=,
∴=,
又∵∠DAE=∠CAB,
∴△ADE∽△ACB,
∴∠ADG=∠C,
∵AF为角平分线,
∴∠DAG=∠FAE
∴△ADG∽△ACF,
∴==,
∴=2.
21.证明:∵∠DAB=∠CAE,
∴∠DAB+∠BAE=∠CAE+∠BAE,
即∠DAE=∠BAC,
∵AD=AE,AB=AC,
∴∠D=∠E=,∠B=∠C=,
∴∠D=∠E=∠B=∠C,
∴△ABC∽△ADE.
22.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠C+∠D=180°,∠BAF=∠AED,
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
23.解:(1)BD=t.
(2)∵PD∥BC,AB=AC=15,
∴,
∴AD=AP=15﹣t,
∴BD=CP=t,
∵AC=15,BC=10,CP=t,
∴PD=10﹣t,
∵△ADP和△BDQ相似,
∴或,
∴或,
解得:t1=4,t2=15(舍去),t3=15>10(舍去),t4=6
答:t=4或6时,△ADP与△BDQ相似.
24.证明:∵BF∥DE,
∴=,
∵AD=BD,
∴AC=CG.
(2)解:当PB=5或时,△BCP与△BCD相似;
在△ABC和△GBC中:
,
∴△ABC≌△GBC(SAS),
∴AB=BG
∴∠DBC=∠CBP,
∵AC=6,BC=8,
∴AB=10,
∴CD=5,
∵∠DBC=∠CBP,
第一种情况:若∠DCB=∠BCP,如图1:
在△BCP与△BCD中
∠DCB=∠BCP,
BC=BC,
∠DBC=∠CBP,
∴△BCP≌△BCD(ASA),
∴BP=CD=5;
第二种情况:若∠PCB=∠DCB,如图2:
∵∠CBD=∠CBP,
∴△BPC∽△BCD,
∴,
∴BP=,
综上所述:当PB=5或时,△BCP与△BCD相似.
25.解:(1)∵AO=3CO=6,
∴CO=2,
∴C(2,0),A(0,6).
设BO=x,且x>0;则BC2=(2+x)2,AB2=AO2+OB2=36+x2;
又∵BC=AB,
∴(2+x)2=36+x2,解得x=8,
∴B(﹣8,0);
(2)如图1,过F点作FK⊥BC于K,
可设F点移动的时间为t,且0<t<2,
则:BF=5t,TO=FK=3t;∴AT=6﹣3t,
又∵FE∥BC,
∴△AFE∽△ABC,
而AO⊥BC交EF于T,
则:=,∴=即EF=10﹣5t,
故S△EFO=EF×TO=(10﹣5t)×3t,
即S△EFO=﹣(t﹣2)t,
∴当t=1时,△EFO的面积达到最大值;
此时BF=FA,EF恰好为△ABC的中位线.
则:=,
又有AO⊥BC于O,
则:==,
∴==,
∴△EFO∽△CBA.
26.证明:∵在△ABC中,AD、BE分别是BC、AC边上的高,
∴∠ADC=∠BEC=90°,
∵∠C是公共角,
∴△CDA∽△CEB,
∴CD:CE=CA:CB,
∴CD:CA=CE:CB,
∴△DCE∽△ACB.
27.解:乙同学的解答不正确,
与△ABC相似的三角形还有△GFE,应该补上证明如下:
∵DF∥BC,
∴∠GFE=∠ABC,
又∵∠E=∠C,
∴△GFE∽△ABC.
28.解:(1)∵△ACD和△BCE都是等边三角形,
∴AC=CD,CE=CB,∠ACD=∠BCE=60°
∴∠ACE=∠DCB=120°.
∴△ACE≌△DCB(SAS);
(2)∵△ACE≌△DCB,
∴∠CAE=∠CDB.
∵∠ADC=∠CAD=∠ACD=∠CBE=60°,
∴DC∥BE,
∴∠CDB=∠DBE,
∴∠CAE=∠DBE,
∴∠DAF=∠DBA.
∴△ADF∽△BAD.
29.证明:∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,∠ACF=120°,
∵CE是外角平分线,
∴∠ACE=60°,
∴∠BAC=∠ACE,
又∵∠ADB=∠CDE,
∴△ABD∽△CED.
30.证明:如图所示:
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
1.如图,在△ABC中,∠B=90°,AB=4,BC=2,以AC为边作△ACE,∠ACE=90°,AC=CE,延长BC至点D,使CD=5,连接DE.求证:△ABC∽△CED.
2.如图,在△ABC中,D、E分别是边AC、BC的中点,F是BC延长线上一点,∠F=∠B.
(1)若AB=10,求FD的长;
(2)若AC=BC,求证:△CDE∽△DFE.
3.如图,在平面直角坐标系中,已知OA=6厘米,OB=8厘米.点P从点B开始沿BA边向终点A以1厘米/秒的速度移动;点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发,运动时间为t(s).
(1)当t为何值时,△APQ与△AOB相似?
(2)当t为何值时,△APQ的面积为8cm2?
4.如图,点B、D、E在一条直线上,BE交AC于点F,=,且∠BAD=∠CAE.
(1)求证:△ABC∽△ADE;
(2)求证:△AEF∽△BCF.
5.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边以1cm/s的速度向点B运动:点Q从点B开始,沿BC边以2cm/s的速度向点C运动,当点P运动到点B时,运动停止,如果P、Q分别从A、B两点同时出发.
(1)几秒后△PBQ的面积等于8cm2?
(2)几秒后以P、B、Q为顶点的三角形与△ABC相似?
6.如图,已知O是△ABC内一点,D、E、F分别是OA、OB、OC的中点.求证:△ABC∽△DEF.
7.如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
8.如图所示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
(1)求证:△DAE≌△DCF;
(2)求证:△ABG∽△CFG.
9.如图,在Rt△ABC中,∠ACB=90°,点D在AC上
(1)已知:AC=4,BC=2,∠CBD=∠A,求BD的长;
(2)取AB,BD的中点E,F,连接CE,EF,FC,求证:△CEF∽△BAD.
10.如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.
请解答下列问题:
(1)当t为何值时,△CEF是等腰直角三角形?
(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?
11.如图, ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:△BDE是直角三角形;
(2)如果OE⊥CD,试判断△BDE与△DCE是否相似,并说明理由.
12.如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且==.
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)试判断△ABE与△ACD是否相似?并说明理由.
13.在△ABC和△A′B′C′中,已知:AB=6cm,BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm.试证明△ABC与△A′B′C′相似.
14.如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.写出图中三对相似三角形,并证明其中的一对.
15.平行四边形ABCD中,过A作AE⊥BC,垂足为E,连DE.F为线段DE上一点,且∠1=∠B.求证:△ADF∽△DEC.
16.如图,在△ABC中,BA=BC,过C点作CE⊥BC交∠ABC的角平分线BE于点E,连接AE,D是BE上的一点,且∠BAD=∠CAE.求证:△ABD∽△ACE.
17.在△ABC中,AB=8cm,BC=16cm,点P从点A出发沿AB边向点B以2cm/s的速度移动,点Q从B点开始沿BC向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,经几秒钟△BPQ和△BAC相似?
18.如图,三个全等的等腰三角形按如图的形式(B、C、E、G在同一直线上)摆放,连接BF,已知腰长AB=,底边BC=1.
(1)△ABC与△BFG是否相似?试说明理由!
(2)请提出一个与P点有关的问题,并进行解答!
19.如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),且∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x
(1)CD的长度是否随着的x变化而变化?若变化,请用含的x代数式表示CD的长度;若不变化,请求出线段CD的长度;
(2)当x取何值时,△ABP和△CDP相似.
20.如图,在△ABC中,D、E分别是AB、AC上的点,AE=4,AB=6,AD:AC=2:3,△ABC的角平分线AF交DE于点G,交BC于点F.
(1)请你直接写出图中所有的相似三角形;
(2)求AG与GF的比.
21.如图,△ABC与△ADE都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE,求证:△ABC∽△ADE.
22.如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C,求证:△ABF∽△EAD.
23.如图,已知△ABC中,AB=AC=15,BC=10,动点P沿CA方向从点C向点A运动,同时,动点Q沿CB方向从点C向点B运动,速度都为每秒1个单位长度,P、Q中任意一点到达终点时,另一点也随之停止运动.过点P作PD∥BC,交AB边于点D,连接DQ.设P、Q的运动时间为t.
(1)直接写出BD的长;(用含t的代数式表示)
(2)求当t为何值时,△ADP与△BDQ相似.
24.如图,△ABC中,∠C=90°,AC=6,BC=8,点D是AB的中点,点E在DC的延长线上,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
(1)求证:AC=CG;
(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.
25.如图,等腰△ABC中,BA=BC,AO=3CO=6.动点F在BA上以每分钟5个单位长度的速度从B点出发向A点移动,过F作FE∥BC交AC边于E点,连接FO、EO.
(1)求A、B两点的坐标;
(2)证明:当△EFO面积最大时,△EFO∽△CBA.
26.如图,在△ABC中,AD、BE分别是BC、AC边上的高.求证:△DCE∽△ACB.
27.甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”.
甲同学的解答得到了老师的好评.
乙同学的解答是这样的:“与△ABC相似的三角形只有△AFD,证明如下:
∵DF∥CB,
∴△AFD∽△ABC.”
乙同学的解答正确吗?若不正确,请你改正.
28.如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连接AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.
29.如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长与CE交于点E.求证:△ABD∽△CED.
30.在△ABC中,∠BAC=90°,AB=AC,点D是BC边上一点,过点D作∠ADE=45°,DE交AC于点E,求证:△ABD∽△DCE.
参考答案
1.证明:∵∠B=90°,AB=4,BC=2,
∴AC==2,
∵CE=AC,
∴CE=2,
∵CD=5,
∵==,=,
∴=,
∵∠B=90°,∠ACE=90°,
∴∠BAC+∠BCA=90°,∠BCA+∠DCE=90°.
∴∠BAC=∠DCE.
∴△ABC∽△CED.
2.解:(1)∵D、E分别是AC、BC的中点,
∴DE∥AB,DE=AB=5,
∵DE∥AB,
∴∠DEC=∠B,而∠F=∠B,
∴∠DEC=∠F,
∴DF=DE=5;
(2)∵AC=BC,
∴∠A=∠B,
∵∠CDE=∠A,∠CED=∠B,
∴∠CDE=∠B,
∵∠B=∠F,
∴∠CDE=∠F,
∵∠CED=∠DEF,
∴△CDE∽△DFE.
3.解:(1)∵点A(0,6),B(8,0),
∴AO=6,BO=8,
∴AB===10,
∵点P的速度是每秒1个单位,点Q的速度是每秒1个单位,
∴AQ=t,AP=10﹣t,
①∠APQ是直角时,△APQ∽△AOB,
∴,
即,
解得t=>6,舍去;
②∠AQP是直角时,△AQP∽△AOB,
∴,
即,
解得t=,
综上所述,t=秒时,△APQ与△AOB相似;
(2)如图,过点P作PC⊥OA于点C,
则PC=AP sin∠OAB=(10﹣t)×=(10﹣t),
△APQ的面积=×t×(10﹣t)=8,
整理,得:t2﹣10t+20=0,
解得:t=5+>6(舍去),或t=5﹣;
故当t=5﹣s时,△APQ的面积为8cm2.
4.(1)∵∠BAD=∠CAE
∴∠BAD+∠CAD=∠CAE+∠CAD
即∠BAC=∠DAE
在△ABC和△ADE中
=,∠BAC=∠DAE,
∴△ABC∽△ADE;
(2)∵△ABC∽△ADE,
∴∠C=∠E、
在△AEF和△BFC中,∠C=∠E,∠AFE=∠BFC,
∴△AEF∽△BCF.
5.解:(1)设t秒后△PBQ的面积等于8cm,此时,AP=t,BP=6﹣t,BQ=2t,
∵S△PBQ=BP BQ,即(6﹣t)×2t=8,即t2﹣6t+8=0,解得t1=2,t2=4.
∴2秒或4秒后,△PBQ的面积等于8cm2;
(2)设x秒后以P、B、Q为顶点的三角形与△ABC相似,此时,AP=x,BP=6﹣x,BQ=2x,
①若△BPQ∽△BAC,则=,即=,解得x=3;
②若△BPQ∽△BCA,则=,即=,解得x=1.2.
综上所述,1.2秒或3秒后,以P、B、Q为顶点的三角形与△ABC相似.
6.证明:∵D、E、F分别是OA、OB、OC的中点,
∴DE=AB,EF=BC,DF=AC,
即==,
∴△ABC∽△DEF.
7.(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)答:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC﹣∠BAD=∠CBA﹣∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
8.证明:(1)∵正方形ABCD,等腰直角三角形EDF,
∴∠ADC=∠EDF=90°,AD=CD,DE=DF,
∴∠ADE+∠ADF=∠ADF+∠CDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF;
(2)延长BA到M,交ED于点M,
∵△ADE≌△CDF,
∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,
∵∠MAD=∠BCD=90°,
∴∠EAM=∠BCF,
∵∠EAM=∠BAG,
∴∠BAG=∠BCF,
∵∠AGB=∠CGF,
∴△ABG∽△CFG.
9.(1)解:∵∠CBD=∠A,∠BCD=∠ACB,
∴△CBD∽△CAB,
∴=,即=,
∴CD=1,
∴BD==.
(2)证明:∵E、F分别是Rt△ABC、Rt△BCD斜边上的中点,
∴CF=BD,CE=AB.
又∵E、F分别为是AB、BD的中点,
∴EF=AD,
∴===,
∴△CEF∽△BAD.
10.解:(1)当CE=CF时,△CEF是等腰三角形,
∴4t=12﹣2t,
∴t=2.
(2)①当=时,△ECF∽△ADC,
∴=,
∴t=3.
②当=时,△FCE∽△ADC,
∴=,
∴t=,
综上所述,当t=s或3s时,以点E,C,F为顶点的三角形与△ACD相似.
11.(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵OE=OB,
∴OE=OD,
∴∠OBE=∠OEB,∠ODE=∠OED,
∵∠OBE+∠OEB+∠ODE+∠OED=180°,
∴∠BED=∠OEB+∠OED=90°,
∴DE⊥BE,即△BDE是直角三角形;
(2)解:△BDE与△DCE相似.
∵OE⊥CD,
∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵∠OBE=∠OEB,
∴∠DBE=∠CDE,
∵∠BED=∠DEC=90°,
∴△BDE∽△DCE.
12.解:(1)∠BAE与∠CAD相等.
理由:∵==,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAE=∠CAD;
(2)△ABE与△ACD相似.
∵=,
∴=.
在△ABE与△ACD中,
∵=,∠BAE=∠CAD,
∴△ABE∽△ACD.
13.证明:∵AB=6cm,BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm,
∴==,==,==,
∴==,
∴△ABC∽△A′B′C′.
14.解:△AME∽△MFE,△BMD∽△MGD,△AMF∽△BGM,
①∵∠AMD=∠B+∠D,∠BGM=∠DMG+∠D
又∠B=∠A=∠DME=α
∴∠AMF=∠BGM,
∴△AMF∽△BGM;
②∵∠EAM=∠EMF、∠AEM=∠MEF,
∴△EMF∽△EAM;
③∵∠DBM=∠DMG,∠BDM=∠MDG,
∴△DMG∽△DBM.
15.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠DEC,∠C+∠B=180°.
∵∠1=∠B,∠1+∠AFD=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC.
16.解:∵BA=BC,BE平分∠ABC,
∴∠ABE=∠CBE,BE⊥AC(等腰三角形三线合一的性质),
∴∠CBE+∠ACB=90°,
又∵CE⊥BC,
∴∠ACE+∠ACB=90°,
∴∠CBE=∠ACE,
∴∠ABE=∠ACE,
∵∠BAD=∠CAE,
∴△ABD∽△ACE.
17.解:设经t秒钟△BPQ和△BAC相似,
当△BPQ∽△BAC时,=,
即=,
解得,t=2,
当△BPQ∽△BCA时,=,
即=,
解得,t=,
答:经2秒或秒钟△BPQ和△BAC相似.
18.解:
(1)相似,理由如下:
∵△ABC≌△DCE≌△FEG
∴BC=CE=EG=1,
∴BG=2BC=3,FG=AB=
∴==,=,即=,
又∠ACB=∠FGB,
∴△ABC∽△BFG;
(2)A层问题(较浅显的,仅用到了1个知识点).
例如:①求证:∠PCB=∠REB.(或问∠PCB与∠REB是否相等)等;
②求证:PC∥RE,(或问线段PC与RE是否平行)等.
B层问题(有一定思考的,用到了2~3个知识点).
例如:①求证:∠BPC=∠BFG等,求证:BP=PR等;
②求证:△ABP∽△CQP等,求证:△BPC∽△BRE等;
③求证:△ABP∽△DQR等;④求BP:PF的值等.
A层解答举例:求证:PC∥RE
证明:△ABC≌△DCE
∴∠PCB=∠REB
∴PC∥RE
B层解答举例:求证:BP=PR
证明:∠ACB=∠REB,
∴AC∥DE.
又BC=CE,∴BP=PR.
19.解:(1)CD的长度不变化.
理由如下:
如图1,延长CB和PA,记交点为点Q.
∵∠BPC=∠BPA,BC⊥BP,
∴QB=BC(等腰三角形“三合一”的性质).
∵BA⊥MN,CD⊥MN,
∴AB∥CD,
∴△QAB∽△QDC,
∴==,
∴CD=2AB=2×4=8,
即CD=8;
(2)当△BAP∽△CDP时,
∵∠BPC=∠BPA,∠CPD=∠BPA,
∴∠BPA=∠BPC=∠CPD=60°,
∴AP===,
即x=;
如图2,当△BAP∽△PDC时,
∵∠CPB=∠BPA,∠PCD=∠BPA,
∴3∠BPA=90°,
∴∠BPA=30°,
∴AP===4,
即x=4;
即当x=或4时,△ABP和△CDP相似.
20.解:(1)△ADG∽△ACF,△AGE∽△AFB,△ADE∽△ACB;
(2)∵==,=,
∴=,
又∵∠DAE=∠CAB,
∴△ADE∽△ACB,
∴∠ADG=∠C,
∵AF为角平分线,
∴∠DAG=∠FAE
∴△ADG∽△ACF,
∴==,
∴=2.
21.证明:∵∠DAB=∠CAE,
∴∠DAB+∠BAE=∠CAE+∠BAE,
即∠DAE=∠BAC,
∵AD=AE,AB=AC,
∴∠D=∠E=,∠B=∠C=,
∴∠D=∠E=∠B=∠C,
∴△ABC∽△ADE.
22.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠C+∠D=180°,∠BAF=∠AED,
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
23.解:(1)BD=t.
(2)∵PD∥BC,AB=AC=15,
∴,
∴AD=AP=15﹣t,
∴BD=CP=t,
∵AC=15,BC=10,CP=t,
∴PD=10﹣t,
∵△ADP和△BDQ相似,
∴或,
∴或,
解得:t1=4,t2=15(舍去),t3=15>10(舍去),t4=6
答:t=4或6时,△ADP与△BDQ相似.
24.证明:∵BF∥DE,
∴=,
∵AD=BD,
∴AC=CG.
(2)解:当PB=5或时,△BCP与△BCD相似;
在△ABC和△GBC中:
,
∴△ABC≌△GBC(SAS),
∴AB=BG
∴∠DBC=∠CBP,
∵AC=6,BC=8,
∴AB=10,
∴CD=5,
∵∠DBC=∠CBP,
第一种情况:若∠DCB=∠BCP,如图1:
在△BCP与△BCD中
∠DCB=∠BCP,
BC=BC,
∠DBC=∠CBP,
∴△BCP≌△BCD(ASA),
∴BP=CD=5;
第二种情况:若∠PCB=∠DCB,如图2:
∵∠CBD=∠CBP,
∴△BPC∽△BCD,
∴,
∴BP=,
综上所述:当PB=5或时,△BCP与△BCD相似.
25.解:(1)∵AO=3CO=6,
∴CO=2,
∴C(2,0),A(0,6).
设BO=x,且x>0;则BC2=(2+x)2,AB2=AO2+OB2=36+x2;
又∵BC=AB,
∴(2+x)2=36+x2,解得x=8,
∴B(﹣8,0);
(2)如图1,过F点作FK⊥BC于K,
可设F点移动的时间为t,且0<t<2,
则:BF=5t,TO=FK=3t;∴AT=6﹣3t,
又∵FE∥BC,
∴△AFE∽△ABC,
而AO⊥BC交EF于T,
则:=,∴=即EF=10﹣5t,
故S△EFO=EF×TO=(10﹣5t)×3t,
即S△EFO=﹣(t﹣2)t,
∴当t=1时,△EFO的面积达到最大值;
此时BF=FA,EF恰好为△ABC的中位线.
则:=,
又有AO⊥BC于O,
则:==,
∴==,
∴△EFO∽△CBA.
26.证明:∵在△ABC中,AD、BE分别是BC、AC边上的高,
∴∠ADC=∠BEC=90°,
∵∠C是公共角,
∴△CDA∽△CEB,
∴CD:CE=CA:CB,
∴CD:CA=CE:CB,
∴△DCE∽△ACB.
27.解:乙同学的解答不正确,
与△ABC相似的三角形还有△GFE,应该补上证明如下:
∵DF∥BC,
∴∠GFE=∠ABC,
又∵∠E=∠C,
∴△GFE∽△ABC.
28.解:(1)∵△ACD和△BCE都是等边三角形,
∴AC=CD,CE=CB,∠ACD=∠BCE=60°
∴∠ACE=∠DCB=120°.
∴△ACE≌△DCB(SAS);
(2)∵△ACE≌△DCB,
∴∠CAE=∠CDB.
∵∠ADC=∠CAD=∠ACD=∠CBE=60°,
∴DC∥BE,
∴∠CDB=∠DBE,
∴∠CAE=∠DBE,
∴∠DAF=∠DBA.
∴△ADF∽△BAD.
29.证明:∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,∠ACF=120°,
∵CE是外角平分线,
∴∠ACE=60°,
∴∠BAC=∠ACE,
又∵∠ADB=∠CDE,
∴△ABD∽△CED.
30.证明:如图所示:
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
