第3章 代数式 单元综合练习题 2021-2022学年冀教版七年级数学上册(Word版 含答案)
文档属性
| 名称 | 第3章 代数式 单元综合练习题 2021-2022学年冀教版七年级数学上册(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 11:09:07 | ||
图片预览




文档简介
第3章 代数式 单元综合练习题(解析)
2021-2022学年冀教版七年级数学上册
一、选择题
1、某服装店新开张,第一天销售服装a件,第二天比第一天少销售10件,第三天的销售量是第二天的2倍多7件,则第三天销售了( )
A.(2a﹣13)件 B.(2a+6)件 C.(2a﹣10)件 D.(a+10)件
2、若x表示某件物品的原价,则代数式(1+10%)x表示的意义是( )
A.该物品打九折后的价格 B.该物品价格上涨10%后的售价
C.该物品价格下降10%后的售价 D.该物品价格上涨10%时上涨的价格
3、某商店举办促销活动,促销的方法是将原价x元的衣服以(x﹣10)元的价格出售,则下列说法中,能正确表达该商品促销方法的是( )
A.原价减去8元后再打8折 B.原价打8折后再减去8元
C.原价打2折后再减去8元 D.原价打8折后再减去10元
4、下列式子①,②,③,④,⑤,⑥,⑦,⑧,
其中代数式有( )
A.3个 B.4个 C.5个 D.6个
5、下列各式:(1)1a2b;(2)a 3;(3)20%x;(4)﹣b÷c;(5);(6)m﹣3℃,其中符合代数式书写要求的有( )
A.5个 B.4个 C.3个 D.2个
6、如图为四点在数轴上的位置图,其中O为原点,且,,若点C所表示的数为x,则点B所表示的数为( )
A. B. C. D.
7、已知x﹣2y=2,则代数式3x﹣6y+2014的值是( )
A.2016 B.2018 C.2020 D.2021
8、如图,阴影部分面积的表达式为( )
A.abπa2 B.abπa2 C.ab﹣πa2 D.abπa2
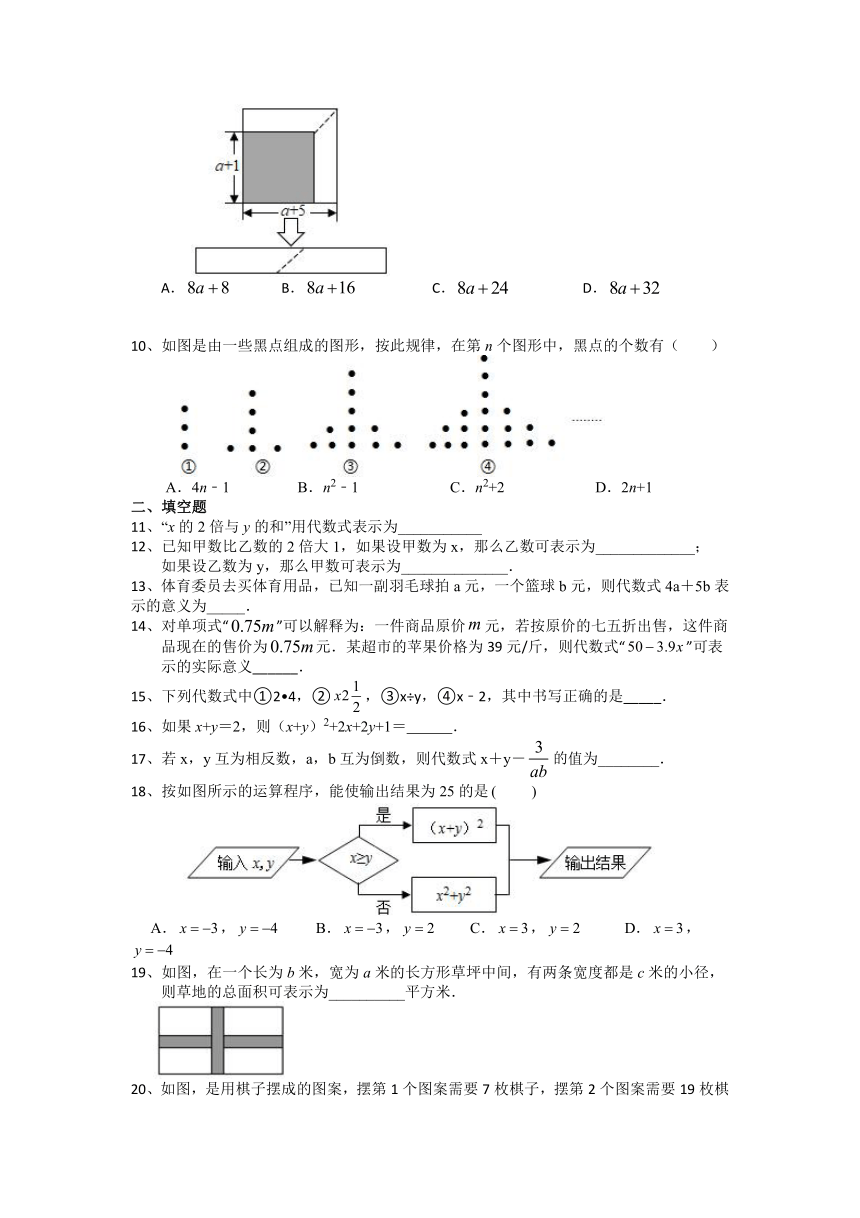
9、如图,从边长为的正方形纸片中剪去一个边长为的正方形,将剩余部分沿虚线剪拼成一个不重叠、无缝隙的长方形,那么该长方形的面积为( )
A. B. C. D.
10、如图是由一些黑点组成的图形,按此规律,在第n个图形中,黑点的个数有( )
A.4n﹣1 B.n2﹣1 C.n2+2 D.2n+1
二、填空题
11、“x的2倍与y的和”用代数式表示为___________
12、已知甲数比乙数的2倍大1,如果设甲数为x,那么乙数可表示为_____________;
如果设乙数为y,那么甲数可表示为______________.
13、体育委员去买体育用品,已知一副羽毛球拍a元,一个篮球b元,则代数式4a+5b表示的意义为_____.
14、对单项式“”可以解释为:一件商品原价元,若按原价的七五折出售,这件商品现在的售价为元.某超市的苹果价格为39元/斤,则代数式“”可表示的实际意义______.
15、下列代数式中①2 4,②,③x÷y,④x﹣2,其中书写正确的是_____.
16、如果x+y=2,则(x+y)2+2x+2y+1= .
17、若x,y互为相反数,a,b互为倒数,则代数式x+y-值为________.
18、按如图所示的运算程序,能使输出结果为25的是
A., B., C., D.,
19、如图,在一个长为b米,宽为a米的长方形草坪中间,有两条宽度都是c米的小径,则草地的总面积可表示为__________平方米.
20、如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要 枚棋子,摆第n个图案需要 枚棋子.
三、解答题
21、(1)当时,求的值;
(2)当时,求的值.
22、求代数式的值.
(1)已知: ,求的值;
(2)当时,求的值;
(3)已知:,求的值;
(4)与互为相反数,求代数式的值.
23、观察图示,解答问题.
(1)由上而下第8行,白球有 个,黑球有 个;
(2)若第为正整数)行白球与黑球的总数记作,求与的关系式;
(3)求出第2020行白球和黑球的总数.
24、课本告诉我们,同一个代数式可以表示不同的实际意义,这体现了不同背景实际问题中的相同数量关系常常可以用同一个代数式来表示.
下列情境中的字母、表示的是两个不超过100的正整数,且,请解决以下问题:
(1)两根同样长的铁丝,分别围成一个长为、宽为的长方形和一个正方形,长方形的长比正方形的边长大多少?
(2)下列情境:①、两数的平均数为;②甲、乙两人分别有元和元,要使两人的钱数一样,则甲需要给乙元;③小亮在超市买了牛奶和可乐共瓶,其中牛奶比可乐少瓶,则他买了瓶牛奶;④小红和爷爷从相距的两地相向而行,1后相遇,相遇时小红比爷爷多行了,则爷爷的平均速度是.上述情境中的、、、也可以用(1)的结果中的代数式表示的是______.(填写所有正确选项前的序号)
25、某仓库一周天内进出货物的吨数如下(“”表示进库,“”表示出库):.
(1)经过这天,仓库里的货物是增多还是减少了?增多或减少了多少吨?
(2)如果货物进仓库的装卸费是元/吨、货物出仓库的装卸费是元/吨,求这天要付的装卸费是多少元? (用含的代数式表示)
26、某市居民使用自来水接如下标准收费(水费按月缴纳)
居民月用水量 不超过的部分 超过但不超过的部分 超过的部分
单价 2元/ 3元/ 4元/
(1)某用户一个月用了水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为n立方米,当时,求该用户应缴纳的水费(用含n的代数式表示);
(3)甲、乙两用户一个月共用水,已知甲用户缴纳的水费超过了20元,设甲用户这个月用水,则甲、乙两用户一个月共缴纳的水费为________元(用含x的代数式表示直接写出答案).
第3章 代数式 单元综合练习题(解析)
2021-2022学年冀教版七年级数学上册
一、选择题
1、某服装店新开张,第一天销售服装a件,第二天比第一天少销售10件,第三天的销售量是第二天的2倍多7件,则第三天销售了( )
A.(2a﹣13)件 B.(2a+6)件 C.(2a﹣10)件 D.(a+10)件
【解题思路】首先求得第二天销售服装(a﹣10)件,则第三天销售了[2(a﹣10)+7]件,进一步整理得出答案即可.
【解答过程】解:由题意可知:
第三天销售量是2(a﹣10)+7=(2a﹣13)件.
故选:A.
2、若x表示某件物品的原价,则代数式(1+10%)x表示的意义是( )
A.该物品打九折后的价格 B.该物品价格上涨10%后的售价
C.该物品价格下降10%后的售价 D.该物品价格上涨10%时上涨的价格
【解题思路】说出代数式的意义,实际上就是把代数式用语言叙述出来.叙述时,要求既要表明运算的顺序,又要说出运算的最终结果.
【解答过程】解:若x表示某件物品的原价,则代数式(1+10%)x表示的意义是该物品价格上涨10%后的售价.
故选:B.
3、某商店举办促销活动,促销的方法是将原价x元的衣服以(x﹣10)元的价格出售,则下列说法中,能正确表达该商品促销方法的是( )
A.原价减去8元后再打8折 B.原价打8折后再减去8元
C.原价打2折后再减去8元 D.原价打8折后再减去10元
【解题思路】根据代数式的实际意义即可得结论.
【解答过程】解:将原价x元的衣服以(x﹣10)元的价格出售,
能正确表达该商店促销方法的是:原价减去10元后再打8折;或原价打8折后再减去8元.
故选:B.
4、下列式子①,②,③,④,⑤,⑥,⑦,⑧,
其中代数式有( )
A.3个 B.4个 C.5个 D.6个
【答案】C
【分析】代数式是运算符号把数和表示数的字母连接而成的式子,据此确定解答即可.
【详解】解:代数式是运算符号把数和表示数的字母连接而成的式子,
所以以上八个式子中,是代数式的有①③⑥⑦⑧五个.故选:C
5、下列各式:(1)1a2b;(2)a 3;(3)20%x;(4)﹣b÷c;(5);(6)m﹣3℃,其中符合代数式书写要求的有( )
A.5个 B.4个 C.3个 D.2个
【解题思路】根据代数式的书写规则,对各小题的代数式进行判断,即可求出答案.
【解答过程】解:(1)1a2b中分数不能为带分数,故原式书写错误;
(2)a 3数与字母相乘要数在前,字母在后并省略乘号,故原式书写错误;
(3)20%x书写正确;
(4)﹣b÷c除号应用分数线,故原式书写错误;
(5)书写正确;
(6)m﹣3℃应该加括号,故原式书写错误;
符合代数式书写要求的有2个.
故选:D.
6、如图为四点在数轴上的位置图,其中O为原点,且,,若点C所表示的数为x,则点B所表示的数为( )
A. B. C. D.
【答案】B
【分析】首先表示A所表示的数,再根据O为原点,OA=OB可得B表示的数和A表示的数是互为相反数,进而可得答案.
【详解】解:∵AC=1,点C所表示的数为x,∴点A表示的数为x-1,
∵O为原点,OA=OB,∴点B所表示的数为-(x-1),
故选:B.
7、已知x﹣2y=2,则代数式3x﹣6y+2014的值是( )
A.2016 B.2018 C.2020 D.2021
【答案】C
【分析】通过提公因式,进行整体代换,代入数值,再进行计算即可.
【解析】解:∵x﹣2y=2,
∴原式=3(x﹣2y)+2014=3×2+2014=2020,
故选:C.
8、如图,阴影部分面积的表达式为( )
A.abπa2 B.abπa2 C.ab﹣πa2 D.abπa2
【解题思路】直接利用矩形面积减去圆的面积进而得出答案.
【解答过程】解:阴影部分面积的表达式为:ab﹣π×()2=abπa2.
故选:D.
9、如图,从边长为的正方形纸片中剪去一个边长为的正方形,将剩余部分沿虚线剪拼成一个不重叠、无缝隙的长方形,那么该长方形的面积为( )
A. B. C. D.
【答案】C
【分析】对照剪拼前的图形,求出剪拼后的长方形的长和宽,即可求出面积.
【详解】解:根据题意得:长方形的宽为(a+5)-(a+1)=4,
长方形的长为(a+5)+(a+1)=2a+6,∴长方形的面积为4(2a+6)=8a+24,
故选:C.
10、如图是由一些黑点组成的图形,按此规律,在第n个图形中,黑点的个数有( )
A.4n﹣1 B.n2﹣1 C.n2+2 D.2n+1
【分析】分析数据可得:第①个图形中点的个数为3;第②个图形中点的个数为3+3;第③个图形中点的个数为3+3+5;第④个图形中点的个数为3+3+5+7;…则知第n个图形中小圆的个数为3+3+5+7+…+(2n﹣1).据此可以求得答案.
【答案】解:第①个图形中点的个数为3;
第②个图形中点的个数为3+3;
第③个图形中点的个数为3+3+5;
第④个图形中点的个数为3+3+5+7;
…
第n个图形中小圆的个数为3+3+5+7+…+(2n﹣1)=n2+2.
故选:C.
二、填空题
11、“x的2倍与y的和”用代数式表示为___________
【答案】
【分析】x的2倍即2x,根据语句列式即可.
【详解】
“x的2倍与y的和”用代数式表示为2x+y,
12、已知甲数比乙数的2倍大1,如果设甲数为x,那么乙数可表示为_____________;
如果设乙数为y,那么甲数可表示为______________.
【答案】 2y+1
【分析】
甲数比乙数的2倍大1,即是已知相等关系:甲数=2×乙数+1.
【详解】
解:如果设甲数为x,那么乙数可表示为;
如果设乙数为y,那么甲数可表示为2y+1.
故答案是:;2y+1.
13、体育委员去买体育用品,已知一副羽毛球拍a元,一个篮球b元,则代数式4a+5b表示的意义为_____.
【答案】买4副羽毛球拍、5个篮球需要的钱数
【解析】
【分析】根据题意,可得4a表示买4副羽毛球拍的钱,5b表示买5个篮球需要的钱数.
【详解】根据题意,可得代数式4a+5b表示的意义为买4副羽毛球拍、5个篮球需要的钱数.
故答案为买4副羽毛球拍、5个篮球需要的钱数
14、对单项式“”可以解释为:一件商品原价元,若按原价的七五折出售,这件商品现在的售价为元.某超市的苹果价格为39元/斤,则代数式“”可表示的实际意义______.
【答案】用50元买原价39元/斤一折出售的苹果斤后余下的钱.
【分析】根据代数式,50是支付的钱,按原价一折,购买x斤的钱,其差表示余下的钱即可.
【详解】解:按原价一折,购买x斤的钱,代数式“”可表示的实际意义是:支付50元买原价39元/斤一折出售的苹果x斤后余下的钱,
故答案为:用50元买原价39元/斤一折出售的苹果斤后余下的钱.
15、下列代数式中①2 4,②,③x÷y,④x﹣2,其中书写正确的是_____.
【答案】④.
【解析】①2 4应为2×4;②x2应为x;③x÷y应为;④x-2书写正确,
综上所述,书写正确的是④.
16、如果x+y=2,则(x+y)2+2x+2y+1= .
【分析】将x+y=2代入(x+y)2+2x+2y+1=(x+y)2+2(x+y)+1可得结果.
【解答】解:∵x+y=2,
∴原式=(x+y)2+2(x+y)+1=22+2×2+1=9,
故答案为:9.
17、若x,y互为相反数,a,b互为倒数,则代数式x+y-值为________.
【答案】-3
【解析】
【分析】
【详解】若x,y互为相反数,a,b互为倒数,则x+y=0,ab=1,
所以,x+y-=0-3=-3
故答案为-3
18、按如图所示的运算程序,能使输出结果为25的是
A., B., C., D.,
【解答】解:当,时,,
当,时,,
当,时,,
当,时,.
故选:.
19、如图,在一个长为b米,宽为a米的长方形草坪中间,有两条宽度都是c米的小径,则草地的总面积可表示为__________平方米.
【答案】
【分析】分别求出小径的面积和长方形的面积,再得出答案即可.
【详解】解:草地的总面积可表示为平方米,
故答案为:平方米.
20、如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要 枚棋子,摆第n个图案需要 枚棋子.
【答案】127 ()
【解析】
∵n=1时,总数是6+1=7;
n=2时,总数为6×(1+2)+1=19;
n=3时,总数为6×(1+2+3)+1=37枚;
…;
∴n=6时,总数为6×(1+2+3…+6)+1=127枚;
…;
∴n=n时,有6×(1+2+3+…n)+1=6×(n+1)n/2+1=(3n2+3n+1)枚.
故答案为127,3n2+3n+1.
三、解答题
21、(1)当时,求的值;
(2)当时,求的值.
【答案】(1)7;(2)
【分析】
(1)把,代人代数式求解即可;
(2)把,代入代数式求解即可.
【解析】
解:(1)把,代人得;
原式;
(2)把,代入:
原式.
22、求代数式的值.
(1)已知: ,求的值;
(2)当时,求的值;
(3)已知:,求的值;
(4)与互为相反数,求代数式的值.
【答案】(1)3;(2);(3)13;(4)
【分析】(1)、(2)直接将字母的取值代入代数式即可求解;
(3)由,可先求出a的值,再将a、b的值代入代数式求解即可;
(4)由与互为相反数,可知,,从而可得,,然后将式子的值代入代数式即可求解.
【解析】
解:(1)当时,原式;
(2)当,原式;
(3)由得,原式;
(4)若与互为相反数,则;
因为;所以;;
原式,
故的值为.
23、观察图示,解答问题.
(1)由上而下第8行,白球有 个,黑球有 个;
(2)若第为正整数)行白球与黑球的总数记作,求与的关系式;
(3)求出第2020行白球和黑球的总数.
【解答】解:(1)由上而下第1行,白球有1个,黑球有3个;
第2行,白球有2个,黑球有5个;
第3行,白球有3个,黑球有7个;
第8行,白球有8个,黑球有15个;
故答案为:8,15;
(2)第为正整数)行白球数为个,
黑球数为:个,
所以总数与的关系式为:;
(3)第2020行白球和黑球的总数为:.
24、课本告诉我们,同一个代数式可以表示不同的实际意义,这体现了不同背景实际问题中的相同数量关系常常可以用同一个代数式来表示.
下列情境中的字母、表示的是两个不超过100的正整数,且,请解决以下问题:
(1)两根同样长的铁丝,分别围成一个长为、宽为的长方形和一个正方形,长方形的长比正方形的边长大多少?
(2)下列情境:①、两数的平均数为;②甲、乙两人分别有元和元,要使两人的钱数一样,则甲需要给乙元;③小亮在超市买了牛奶和可乐共瓶,其中牛奶比可乐少瓶,则他买了瓶牛奶;④小红和爷爷从相距的两地相向而行,1后相遇,相遇时小红比爷爷多行了,则爷爷的平均速度是.上述情境中的、、、也可以用(1)的结果中的代数式表示的是______.(填写所有正确选项前的序号)
【答案】(1)长方形的长比正方形的边长大;(2)②③④
【分析】(1)分别表示长方形和正方形的边长,再作差即可得出结论;(2)根据题意逐项列式,即可看出.
【详解】(1)
答:长方形的长比正方形的边长大.
(2)①,② ,③,
④ ,故答案为:②③④.
25、某仓库一周天内进出货物的吨数如下(“”表示进库,“”表示出库):.
(1)经过这天,仓库里的货物是增多还是减少了?增多或减少了多少吨?
(2)如果货物进仓库的装卸费是元/吨、货物出仓库的装卸费是元/吨,求这天要付的装卸费是多少元? (用含的代数式表示)
【答案】(1)减少了25吨;(2)元
【分析】
(1)求出这7天进出货物的质量和,根据结果的符号和绝对值进行判断即可求出最终水泥的增减量.
(2)分别求出进出货物的总吨数,即各个数的绝对值的和,再求出总装卸费.
【详解】
解:(1)=,
∴经过这7天,仓库里的货物减少了25吨;
(2)由题意得:
进库的总装卸费为: =
出库的总装卸费为:
∴这7天要付元装卸费.
26、某市居民使用自来水接如下标准收费(水费按月缴纳)
居民月用水量 不超过的部分 超过但不超过的部分 超过的部分
单价 2元/ 3元/ 4元/
(1)某用户一个月用了水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为n立方米,当时,求该用户应缴纳的水费(用含n的代数式表示);
(3)甲、乙两用户一个月共用水,已知甲用户缴纳的水费超过了20元,设甲用户这个月用水,则甲、乙两用户一个月共缴纳的水费为________元(用含x的代数式表示直接写出答案).
【答案】(1)35元;(2)4n-28元;(3)106-x或2x+44或x+70
【分析】
(1)根据收费标准进行计算即可;
(2)根据收费标准列代数式即可;
(3)由题意可知甲用户的用水量大于10m3,再分三种情况,根据收费标准列出代数式即可.
【详解】
解:(1)10×2+(15-10)×3=20+15=35元,
∴该用户这个月应缴纳水费35元;
(2)∵n>18,
∴该用户应缴纳的水费为:10×2+(18-10)×3+(n-18)×4=4n-28(元);
(3)∵甲用户缴纳的水费超过了20元,
∴甲用户的用水量大于10m3,
当10<x≤18时,则18≤36-x,此时共缴纳的水费为:10×2+(x-10)×3+4×(36-x)-28=106-x(元);
当x>18,0<36-x≤10时,此时共缴纳的水费为:4x-28+(36-x)×2=2x+44(元);
当x>18,10<36-x<18时,此时共缴纳的水费为:4x-28+10×2+(36-x-10)×3=x+70(元).
2021-2022学年冀教版七年级数学上册
一、选择题
1、某服装店新开张,第一天销售服装a件,第二天比第一天少销售10件,第三天的销售量是第二天的2倍多7件,则第三天销售了( )
A.(2a﹣13)件 B.(2a+6)件 C.(2a﹣10)件 D.(a+10)件
2、若x表示某件物品的原价,则代数式(1+10%)x表示的意义是( )
A.该物品打九折后的价格 B.该物品价格上涨10%后的售价
C.该物品价格下降10%后的售价 D.该物品价格上涨10%时上涨的价格
3、某商店举办促销活动,促销的方法是将原价x元的衣服以(x﹣10)元的价格出售,则下列说法中,能正确表达该商品促销方法的是( )
A.原价减去8元后再打8折 B.原价打8折后再减去8元
C.原价打2折后再减去8元 D.原价打8折后再减去10元
4、下列式子①,②,③,④,⑤,⑥,⑦,⑧,
其中代数式有( )
A.3个 B.4个 C.5个 D.6个
5、下列各式:(1)1a2b;(2)a 3;(3)20%x;(4)﹣b÷c;(5);(6)m﹣3℃,其中符合代数式书写要求的有( )
A.5个 B.4个 C.3个 D.2个
6、如图为四点在数轴上的位置图,其中O为原点,且,,若点C所表示的数为x,则点B所表示的数为( )
A. B. C. D.
7、已知x﹣2y=2,则代数式3x﹣6y+2014的值是( )
A.2016 B.2018 C.2020 D.2021
8、如图,阴影部分面积的表达式为( )
A.abπa2 B.abπa2 C.ab﹣πa2 D.abπa2
9、如图,从边长为的正方形纸片中剪去一个边长为的正方形,将剩余部分沿虚线剪拼成一个不重叠、无缝隙的长方形,那么该长方形的面积为( )
A. B. C. D.
10、如图是由一些黑点组成的图形,按此规律,在第n个图形中,黑点的个数有( )
A.4n﹣1 B.n2﹣1 C.n2+2 D.2n+1
二、填空题
11、“x的2倍与y的和”用代数式表示为___________
12、已知甲数比乙数的2倍大1,如果设甲数为x,那么乙数可表示为_____________;
如果设乙数为y,那么甲数可表示为______________.
13、体育委员去买体育用品,已知一副羽毛球拍a元,一个篮球b元,则代数式4a+5b表示的意义为_____.
14、对单项式“”可以解释为:一件商品原价元,若按原价的七五折出售,这件商品现在的售价为元.某超市的苹果价格为39元/斤,则代数式“”可表示的实际意义______.
15、下列代数式中①2 4,②,③x÷y,④x﹣2,其中书写正确的是_____.
16、如果x+y=2,则(x+y)2+2x+2y+1= .
17、若x,y互为相反数,a,b互为倒数,则代数式x+y-值为________.
18、按如图所示的运算程序,能使输出结果为25的是
A., B., C., D.,
19、如图,在一个长为b米,宽为a米的长方形草坪中间,有两条宽度都是c米的小径,则草地的总面积可表示为__________平方米.
20、如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要 枚棋子,摆第n个图案需要 枚棋子.
三、解答题
21、(1)当时,求的值;
(2)当时,求的值.
22、求代数式的值.
(1)已知: ,求的值;
(2)当时,求的值;
(3)已知:,求的值;
(4)与互为相反数,求代数式的值.
23、观察图示,解答问题.
(1)由上而下第8行,白球有 个,黑球有 个;
(2)若第为正整数)行白球与黑球的总数记作,求与的关系式;
(3)求出第2020行白球和黑球的总数.
24、课本告诉我们,同一个代数式可以表示不同的实际意义,这体现了不同背景实际问题中的相同数量关系常常可以用同一个代数式来表示.
下列情境中的字母、表示的是两个不超过100的正整数,且,请解决以下问题:
(1)两根同样长的铁丝,分别围成一个长为、宽为的长方形和一个正方形,长方形的长比正方形的边长大多少?
(2)下列情境:①、两数的平均数为;②甲、乙两人分别有元和元,要使两人的钱数一样,则甲需要给乙元;③小亮在超市买了牛奶和可乐共瓶,其中牛奶比可乐少瓶,则他买了瓶牛奶;④小红和爷爷从相距的两地相向而行,1后相遇,相遇时小红比爷爷多行了,则爷爷的平均速度是.上述情境中的、、、也可以用(1)的结果中的代数式表示的是______.(填写所有正确选项前的序号)
25、某仓库一周天内进出货物的吨数如下(“”表示进库,“”表示出库):.
(1)经过这天,仓库里的货物是增多还是减少了?增多或减少了多少吨?
(2)如果货物进仓库的装卸费是元/吨、货物出仓库的装卸费是元/吨,求这天要付的装卸费是多少元? (用含的代数式表示)
26、某市居民使用自来水接如下标准收费(水费按月缴纳)
居民月用水量 不超过的部分 超过但不超过的部分 超过的部分
单价 2元/ 3元/ 4元/
(1)某用户一个月用了水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为n立方米,当时,求该用户应缴纳的水费(用含n的代数式表示);
(3)甲、乙两用户一个月共用水,已知甲用户缴纳的水费超过了20元,设甲用户这个月用水,则甲、乙两用户一个月共缴纳的水费为________元(用含x的代数式表示直接写出答案).
第3章 代数式 单元综合练习题(解析)
2021-2022学年冀教版七年级数学上册
一、选择题
1、某服装店新开张,第一天销售服装a件,第二天比第一天少销售10件,第三天的销售量是第二天的2倍多7件,则第三天销售了( )
A.(2a﹣13)件 B.(2a+6)件 C.(2a﹣10)件 D.(a+10)件
【解题思路】首先求得第二天销售服装(a﹣10)件,则第三天销售了[2(a﹣10)+7]件,进一步整理得出答案即可.
【解答过程】解:由题意可知:
第三天销售量是2(a﹣10)+7=(2a﹣13)件.
故选:A.
2、若x表示某件物品的原价,则代数式(1+10%)x表示的意义是( )
A.该物品打九折后的价格 B.该物品价格上涨10%后的售价
C.该物品价格下降10%后的售价 D.该物品价格上涨10%时上涨的价格
【解题思路】说出代数式的意义,实际上就是把代数式用语言叙述出来.叙述时,要求既要表明运算的顺序,又要说出运算的最终结果.
【解答过程】解:若x表示某件物品的原价,则代数式(1+10%)x表示的意义是该物品价格上涨10%后的售价.
故选:B.
3、某商店举办促销活动,促销的方法是将原价x元的衣服以(x﹣10)元的价格出售,则下列说法中,能正确表达该商品促销方法的是( )
A.原价减去8元后再打8折 B.原价打8折后再减去8元
C.原价打2折后再减去8元 D.原价打8折后再减去10元
【解题思路】根据代数式的实际意义即可得结论.
【解答过程】解:将原价x元的衣服以(x﹣10)元的价格出售,
能正确表达该商店促销方法的是:原价减去10元后再打8折;或原价打8折后再减去8元.
故选:B.
4、下列式子①,②,③,④,⑤,⑥,⑦,⑧,
其中代数式有( )
A.3个 B.4个 C.5个 D.6个
【答案】C
【分析】代数式是运算符号把数和表示数的字母连接而成的式子,据此确定解答即可.
【详解】解:代数式是运算符号把数和表示数的字母连接而成的式子,
所以以上八个式子中,是代数式的有①③⑥⑦⑧五个.故选:C
5、下列各式:(1)1a2b;(2)a 3;(3)20%x;(4)﹣b÷c;(5);(6)m﹣3℃,其中符合代数式书写要求的有( )
A.5个 B.4个 C.3个 D.2个
【解题思路】根据代数式的书写规则,对各小题的代数式进行判断,即可求出答案.
【解答过程】解:(1)1a2b中分数不能为带分数,故原式书写错误;
(2)a 3数与字母相乘要数在前,字母在后并省略乘号,故原式书写错误;
(3)20%x书写正确;
(4)﹣b÷c除号应用分数线,故原式书写错误;
(5)书写正确;
(6)m﹣3℃应该加括号,故原式书写错误;
符合代数式书写要求的有2个.
故选:D.
6、如图为四点在数轴上的位置图,其中O为原点,且,,若点C所表示的数为x,则点B所表示的数为( )
A. B. C. D.
【答案】B
【分析】首先表示A所表示的数,再根据O为原点,OA=OB可得B表示的数和A表示的数是互为相反数,进而可得答案.
【详解】解:∵AC=1,点C所表示的数为x,∴点A表示的数为x-1,
∵O为原点,OA=OB,∴点B所表示的数为-(x-1),
故选:B.
7、已知x﹣2y=2,则代数式3x﹣6y+2014的值是( )
A.2016 B.2018 C.2020 D.2021
【答案】C
【分析】通过提公因式,进行整体代换,代入数值,再进行计算即可.
【解析】解:∵x﹣2y=2,
∴原式=3(x﹣2y)+2014=3×2+2014=2020,
故选:C.
8、如图,阴影部分面积的表达式为( )
A.abπa2 B.abπa2 C.ab﹣πa2 D.abπa2
【解题思路】直接利用矩形面积减去圆的面积进而得出答案.
【解答过程】解:阴影部分面积的表达式为:ab﹣π×()2=abπa2.
故选:D.
9、如图,从边长为的正方形纸片中剪去一个边长为的正方形,将剩余部分沿虚线剪拼成一个不重叠、无缝隙的长方形,那么该长方形的面积为( )
A. B. C. D.
【答案】C
【分析】对照剪拼前的图形,求出剪拼后的长方形的长和宽,即可求出面积.
【详解】解:根据题意得:长方形的宽为(a+5)-(a+1)=4,
长方形的长为(a+5)+(a+1)=2a+6,∴长方形的面积为4(2a+6)=8a+24,
故选:C.
10、如图是由一些黑点组成的图形,按此规律,在第n个图形中,黑点的个数有( )
A.4n﹣1 B.n2﹣1 C.n2+2 D.2n+1
【分析】分析数据可得:第①个图形中点的个数为3;第②个图形中点的个数为3+3;第③个图形中点的个数为3+3+5;第④个图形中点的个数为3+3+5+7;…则知第n个图形中小圆的个数为3+3+5+7+…+(2n﹣1).据此可以求得答案.
【答案】解:第①个图形中点的个数为3;
第②个图形中点的个数为3+3;
第③个图形中点的个数为3+3+5;
第④个图形中点的个数为3+3+5+7;
…
第n个图形中小圆的个数为3+3+5+7+…+(2n﹣1)=n2+2.
故选:C.
二、填空题
11、“x的2倍与y的和”用代数式表示为___________
【答案】
【分析】x的2倍即2x,根据语句列式即可.
【详解】
“x的2倍与y的和”用代数式表示为2x+y,
12、已知甲数比乙数的2倍大1,如果设甲数为x,那么乙数可表示为_____________;
如果设乙数为y,那么甲数可表示为______________.
【答案】 2y+1
【分析】
甲数比乙数的2倍大1,即是已知相等关系:甲数=2×乙数+1.
【详解】
解:如果设甲数为x,那么乙数可表示为;
如果设乙数为y,那么甲数可表示为2y+1.
故答案是:;2y+1.
13、体育委员去买体育用品,已知一副羽毛球拍a元,一个篮球b元,则代数式4a+5b表示的意义为_____.
【答案】买4副羽毛球拍、5个篮球需要的钱数
【解析】
【分析】根据题意,可得4a表示买4副羽毛球拍的钱,5b表示买5个篮球需要的钱数.
【详解】根据题意,可得代数式4a+5b表示的意义为买4副羽毛球拍、5个篮球需要的钱数.
故答案为买4副羽毛球拍、5个篮球需要的钱数
14、对单项式“”可以解释为:一件商品原价元,若按原价的七五折出售,这件商品现在的售价为元.某超市的苹果价格为39元/斤,则代数式“”可表示的实际意义______.
【答案】用50元买原价39元/斤一折出售的苹果斤后余下的钱.
【分析】根据代数式,50是支付的钱,按原价一折,购买x斤的钱,其差表示余下的钱即可.
【详解】解:按原价一折,购买x斤的钱,代数式“”可表示的实际意义是:支付50元买原价39元/斤一折出售的苹果x斤后余下的钱,
故答案为:用50元买原价39元/斤一折出售的苹果斤后余下的钱.
15、下列代数式中①2 4,②,③x÷y,④x﹣2,其中书写正确的是_____.
【答案】④.
【解析】①2 4应为2×4;②x2应为x;③x÷y应为;④x-2书写正确,
综上所述,书写正确的是④.
16、如果x+y=2,则(x+y)2+2x+2y+1= .
【分析】将x+y=2代入(x+y)2+2x+2y+1=(x+y)2+2(x+y)+1可得结果.
【解答】解:∵x+y=2,
∴原式=(x+y)2+2(x+y)+1=22+2×2+1=9,
故答案为:9.
17、若x,y互为相反数,a,b互为倒数,则代数式x+y-值为________.
【答案】-3
【解析】
【分析】
【详解】若x,y互为相反数,a,b互为倒数,则x+y=0,ab=1,
所以,x+y-=0-3=-3
故答案为-3
18、按如图所示的运算程序,能使输出结果为25的是
A., B., C., D.,
【解答】解:当,时,,
当,时,,
当,时,,
当,时,.
故选:.
19、如图,在一个长为b米,宽为a米的长方形草坪中间,有两条宽度都是c米的小径,则草地的总面积可表示为__________平方米.
【答案】
【分析】分别求出小径的面积和长方形的面积,再得出答案即可.
【详解】解:草地的总面积可表示为平方米,
故答案为:平方米.
20、如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要 枚棋子,摆第n个图案需要 枚棋子.
【答案】127 ()
【解析】
∵n=1时,总数是6+1=7;
n=2时,总数为6×(1+2)+1=19;
n=3时,总数为6×(1+2+3)+1=37枚;
…;
∴n=6时,总数为6×(1+2+3…+6)+1=127枚;
…;
∴n=n时,有6×(1+2+3+…n)+1=6×(n+1)n/2+1=(3n2+3n+1)枚.
故答案为127,3n2+3n+1.
三、解答题
21、(1)当时,求的值;
(2)当时,求的值.
【答案】(1)7;(2)
【分析】
(1)把,代人代数式求解即可;
(2)把,代入代数式求解即可.
【解析】
解:(1)把,代人得;
原式;
(2)把,代入:
原式.
22、求代数式的值.
(1)已知: ,求的值;
(2)当时,求的值;
(3)已知:,求的值;
(4)与互为相反数,求代数式的值.
【答案】(1)3;(2);(3)13;(4)
【分析】(1)、(2)直接将字母的取值代入代数式即可求解;
(3)由,可先求出a的值,再将a、b的值代入代数式求解即可;
(4)由与互为相反数,可知,,从而可得,,然后将式子的值代入代数式即可求解.
【解析】
解:(1)当时,原式;
(2)当,原式;
(3)由得,原式;
(4)若与互为相反数,则;
因为;所以;;
原式,
故的值为.
23、观察图示,解答问题.
(1)由上而下第8行,白球有 个,黑球有 个;
(2)若第为正整数)行白球与黑球的总数记作,求与的关系式;
(3)求出第2020行白球和黑球的总数.
【解答】解:(1)由上而下第1行,白球有1个,黑球有3个;
第2行,白球有2个,黑球有5个;
第3行,白球有3个,黑球有7个;
第8行,白球有8个,黑球有15个;
故答案为:8,15;
(2)第为正整数)行白球数为个,
黑球数为:个,
所以总数与的关系式为:;
(3)第2020行白球和黑球的总数为:.
24、课本告诉我们,同一个代数式可以表示不同的实际意义,这体现了不同背景实际问题中的相同数量关系常常可以用同一个代数式来表示.
下列情境中的字母、表示的是两个不超过100的正整数,且,请解决以下问题:
(1)两根同样长的铁丝,分别围成一个长为、宽为的长方形和一个正方形,长方形的长比正方形的边长大多少?
(2)下列情境:①、两数的平均数为;②甲、乙两人分别有元和元,要使两人的钱数一样,则甲需要给乙元;③小亮在超市买了牛奶和可乐共瓶,其中牛奶比可乐少瓶,则他买了瓶牛奶;④小红和爷爷从相距的两地相向而行,1后相遇,相遇时小红比爷爷多行了,则爷爷的平均速度是.上述情境中的、、、也可以用(1)的结果中的代数式表示的是______.(填写所有正确选项前的序号)
【答案】(1)长方形的长比正方形的边长大;(2)②③④
【分析】(1)分别表示长方形和正方形的边长,再作差即可得出结论;(2)根据题意逐项列式,即可看出.
【详解】(1)
答:长方形的长比正方形的边长大.
(2)①,② ,③,
④ ,故答案为:②③④.
25、某仓库一周天内进出货物的吨数如下(“”表示进库,“”表示出库):.
(1)经过这天,仓库里的货物是增多还是减少了?增多或减少了多少吨?
(2)如果货物进仓库的装卸费是元/吨、货物出仓库的装卸费是元/吨,求这天要付的装卸费是多少元? (用含的代数式表示)
【答案】(1)减少了25吨;(2)元
【分析】
(1)求出这7天进出货物的质量和,根据结果的符号和绝对值进行判断即可求出最终水泥的增减量.
(2)分别求出进出货物的总吨数,即各个数的绝对值的和,再求出总装卸费.
【详解】
解:(1)=,
∴经过这7天,仓库里的货物减少了25吨;
(2)由题意得:
进库的总装卸费为: =
出库的总装卸费为:
∴这7天要付元装卸费.
26、某市居民使用自来水接如下标准收费(水费按月缴纳)
居民月用水量 不超过的部分 超过但不超过的部分 超过的部分
单价 2元/ 3元/ 4元/
(1)某用户一个月用了水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为n立方米,当时,求该用户应缴纳的水费(用含n的代数式表示);
(3)甲、乙两用户一个月共用水,已知甲用户缴纳的水费超过了20元,设甲用户这个月用水,则甲、乙两用户一个月共缴纳的水费为________元(用含x的代数式表示直接写出答案).
【答案】(1)35元;(2)4n-28元;(3)106-x或2x+44或x+70
【分析】
(1)根据收费标准进行计算即可;
(2)根据收费标准列代数式即可;
(3)由题意可知甲用户的用水量大于10m3,再分三种情况,根据收费标准列出代数式即可.
【详解】
解:(1)10×2+(15-10)×3=20+15=35元,
∴该用户这个月应缴纳水费35元;
(2)∵n>18,
∴该用户应缴纳的水费为:10×2+(18-10)×3+(n-18)×4=4n-28(元);
(3)∵甲用户缴纳的水费超过了20元,
∴甲用户的用水量大于10m3,
当10<x≤18时,则18≤36-x,此时共缴纳的水费为:10×2+(x-10)×3+4×(36-x)-28=106-x(元);
当x>18,0<36-x≤10时,此时共缴纳的水费为:4x-28+(36-x)×2=2x+44(元);
当x>18,10<36-x<18时,此时共缴纳的水费为:4x-28+10×2+(36-x-10)×3=x+70(元).
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
