第25章图形的相似同步达标测评 2021-2022学年冀教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 第25章图形的相似同步达标测评 2021-2022学年冀教版九年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 284.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-26 00:00:00 | ||
图片预览



文档简介
2021-2022学年冀教版九年级数学上册《第25章图形的相似》同步达标测评(附答案)
一.选择题(共12小题,满分48分)
1.已知2x=3y(y≠0),则下面结论成立的是( )
A.= B.= C.= D.=
2.两个相似三角形的最短边分别为5cm和3cm,他们的周长之差为12cm,那么大三角形的周长为( )
A.14 cm B.16 cm C.18 cm D.30 cm
3.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
4.如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的,得到△COD,则CD的长度是( )
A.2 B.1 C.4 D.2
5.如图,已知l1∥l2∥l3,直线AB分别交l1、l2、l3于A、E、B点,直线CD分别交l1、l2、l3于C、F、D三点,且AE=2,BE=4,则的值为( )
A. B. C. D.2
6.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是( )
A.9.3m B.10.5m C.12.4m D.14m
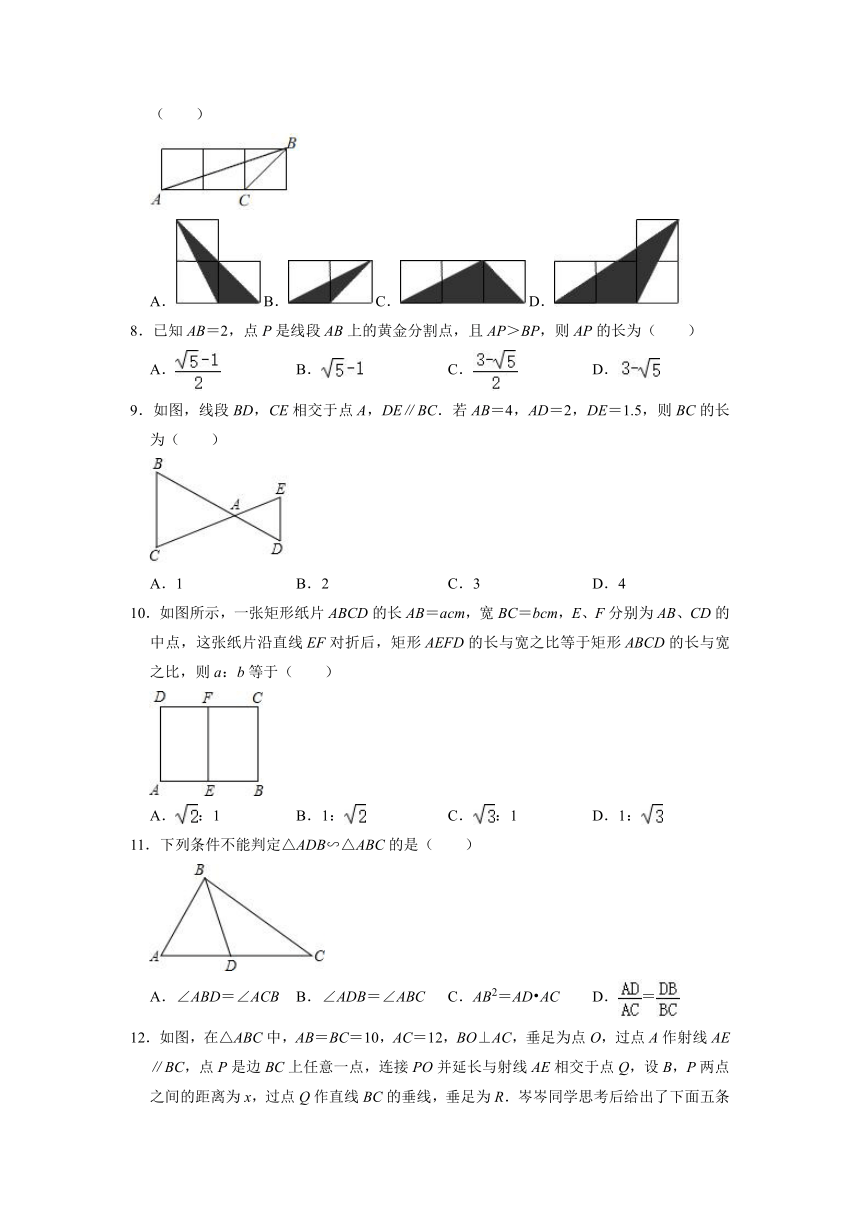
7.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A.B.C.D.
8.已知AB=2,点P是线段AB上的黄金分割点,且AP>BP,则AP的长为( )
A. B. C. D.
9.如图,线段BD,CE相交于点A,DE∥BC.若AB=4,AD=2,DE=1.5,则BC的长为( )
A.1 B.2 C.3 D.4
10.如图所示,一张矩形纸片ABCD的长AB=acm,宽BC=bcm,E、F分别为AB、CD的中点,这张纸片沿直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比,则a:b等于( )
A.:1 B.1: C.:1 D.1:
11.下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B.∠ADB=∠ABC C.AB2=AD AC D.=
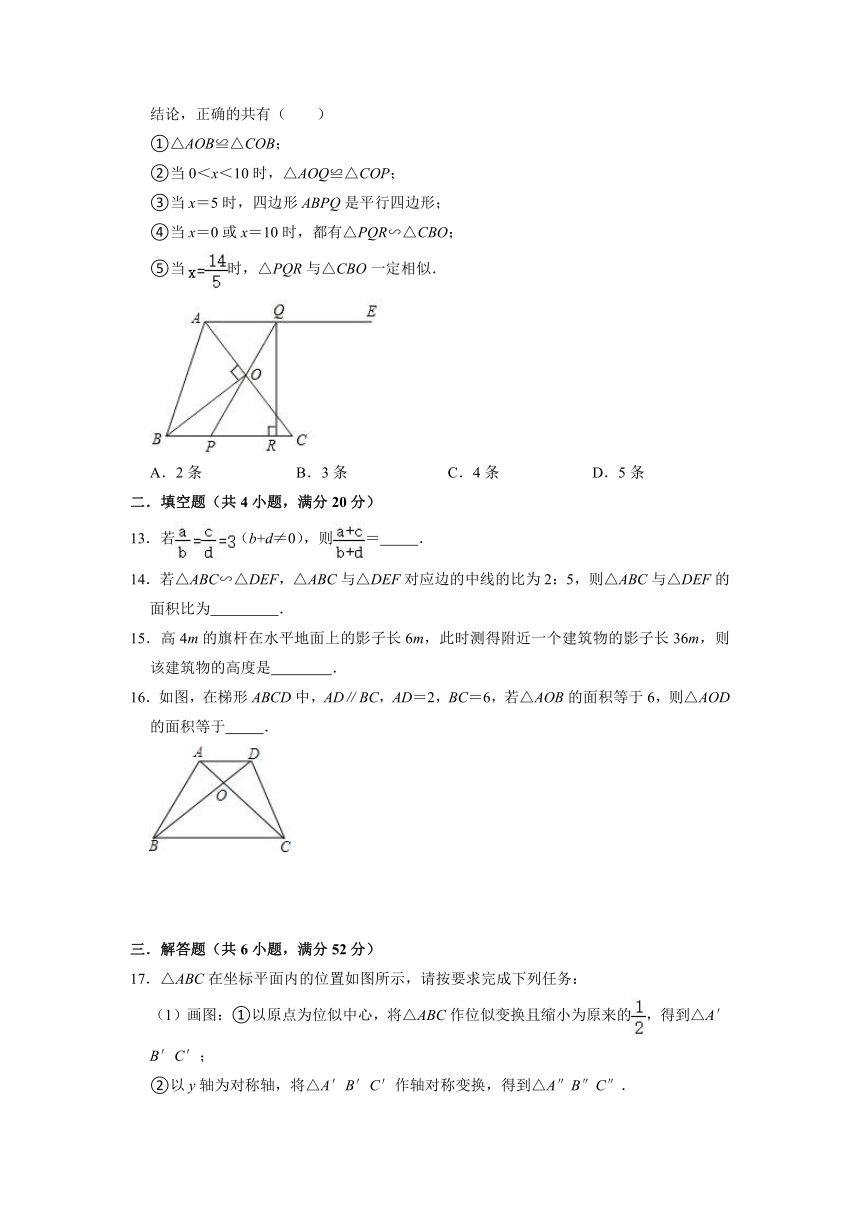
12.如图,在△ABC中,AB=BC=10,AC=12,BO⊥AC,垂足为点O,过点A作射线AE∥BC,点P是边BC上任意一点,连接PO并延长与射线AE相交于点Q,设B,P两点之间的距离为x,过点Q作直线BC的垂线,垂足为R.岑岑同学思考后给出了下面五条结论,正确的共有( )
①△AOB≌△COB;
②当0<x<10时,△AOQ≌△COP;
③当x=5时,四边形ABPQ是平行四边形;
④当x=0或x=10时,都有△PQR∽△CBO;
⑤当时,△PQR与△CBO一定相似.
A.2条 B.3条 C.4条 D.5条
二.填空题(共4小题,满分20分)
13.若(b+d≠0),则= .
14.若△ABC∽△DEF,△ABC与△DEF对应边的中线的比为2:5,则△ABC与△DEF的面积比为 .
15.高4m的旗杆在水平地面上的影子长6m,此时测得附近一个建筑物的影子长36m,则该建筑物的高度是 .
16.如图,在梯形ABCD中,AD∥BC,AD=2,BC=6,若△AOB的面积等于6,则△AOD的面积等于 .
三.解答题(共6小题,满分52分)
17.△ABC在坐标平面内的位置如图所示,请按要求完成下列任务:
(1)画图:①以原点为位似中心,将△ABC作位似变换且缩小为原来的,得到△A′B′C′;
②以y轴为对称轴,将△A′B′C′作轴对称变换,得到△A″B″C″.
(2)填空:如果△ABC内一点M的坐标是(x,y),那么经过上述两次变换后其对应点M″的坐标为 .
18.如图,BE是△ABC的角平分线,延长BE至D,使得BC=CD.
(1)求证:△AEB∽△CED;
(2)若AB=2,BC=4,AE=1,求CE长.
19.如图,一根旗杆AB在某一时刻影子不全落在地面上,有一部分影子落在墙上,测得地面上的影长为3.2m,落在墙上的影长为1.2m,同一时刻测得长为0.8m的竹竿影长为1m,试求出旗杆的高度.
20.已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
21.如图,在△ABC中,∠A=60°,BD⊥AC,垂足为点D,CE⊥AB,垂足为点E.
求证:(1)△ADE∽△ABC.
(2)BC=2DE.
22.如图1,在锐角△ABC中,AD是BC边上的高,BC=6,AD=4,动点P沿线段AD从点A向点D运动,过点P作EF∥BC,EF交AB于E.交AC于F,以EF为边向下作正方形EFGH.
(1)设AP长为x,利用相似三角形的性质.可用含x的代数式表示正方形的边长为EF= ;如图2,当x= 时,GH恰好落在边BC上,此时EF长为 ;
(2)如图3,当GH在△ABC外部,且正方形EFGH与△ABC公共部分的面积为6时,求点P的位置(即求AP的值)
参考答案
一.选择题(共12小题,满分48分)
1.解:A、因为2x=3y,两边都除以2y,得=,故A符合题意;
B、两边除以不同的整式,故B不符合题意;
C、因为2x=3y,两边都除以2y,得=,故C不符合题意;
D、两边除以不同的整式,故D不符合题意;
故选:A.
2.解:根据题意得两三角形的周长的比为5:3,
设两三角形的周长分别为5xcm,3xcm,
则5x﹣3x=12,
解得x=6,
所以5x=30,
即大三角形的周长为30cm.
故选:D.
3.解:3m×2m=6m2,
∴长方形广告牌的成本是120÷6=20元/m2,
将此广告牌的四边都扩大为原来的3倍,
则面积扩大为原来的9倍,
∴扩大后长方形广告牌的面积=9×6=54m2,
∴扩大后长方形广告牌的成本是54×20=1080元,
故选:C.
4.解:∵点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的,得到△COD,
∴C(1,2),则CD的长度是:2.
故选:A.
5.解:∵l1∥l2∥l3,
∴=,
∵AE=2,BE=4,
∴=,
故选:A.
6.解:∵EB∥CD,
∴△ABE∽△ACD,
∴=,即=,
∴CD=10.5(米).
故选:B.
7.解:由正方形的性质可知,∠ACB=180°﹣45°=135°,
A、C、D图形中的钝角都不等于135°,
由勾股定理得,BC=,AC=2,
对应的图形B中的边长分别为1和,
∵=,
∴图B中的三角形(阴影部分)与△ABC相似,
故选:B.
8.解:由于P为线段AB=2的黄金分割点,
且AP>BP,
则AP=×2=﹣1.
故选:B.
9.解:∵DE∥BC,AB=4,AD=2,DE=1.5,
∴,
即,
解得:BC=3,
故选:C.
10.解:∵b:=a:b,
∴a2=2b2,∴a=b,
则a:b=:1.
故选:A.
11.解:A、∵∠ABD=∠ACB,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;
B、∵∠ADB=∠ABC,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;
C、∵AB2=AD AC,∴=,∠A=∠A,△ABC∽△ADB,故此选项不合题意;
D、=不能判定△ADB∽△ABC,故此选项符合题意.
故选:D.
12.解:①∵AB=BC=10,AC=12,BO⊥AC,
∴AO=CO,AB=BC,BO=BO,
∴△AOB≌△COB;
故此选项正确;
②∵AE∥BC,
∴∠AQO=∠OCP,
∵AO=CO,∠AOQ=∠POC,
∴当0<x<10时,△AOQ≌△COP;
故此选项正确;
③当x=5时,
∴BP=PC=5,
∵AQ=PC,
∴AQ=PB=5,
∵AQ∥BC,
∴四边形ABPQ是平行四边形;
故此选项正确;
④当x=0时,P与B重合,
∴∠OBC=∠QPR,
又∵∠BOC=∠PRQ=90°,
∴△BCO∽△PQR;
当x=10时,P与C重合,此时Q与A重合,
∵∠QPR=∠BPO,∠QRP=∠BOC=90°,
∴△QRP∽△BOC,
当x=0时,△BCO∽△PQR与△PQR∽△CBO不相符;故此选项错误;
⑤若△PQR与△CBO一定相似,
则∠QPR=∠BCO,
故OP=OC=6,
过点O作OH⊥BC于H,
由射影定理得CO2=CH CB,
可求得CH=CP=3.6,
故CP=7.2,所以BP=x=2.8
故当时,△PQR与△CBO一定相似.
故此选项正确.
故正确的有4条.
故选:C.
二.填空题(共4小题,满分20分)
13.解:∵==3,
∴a=3b,c=3d,
∴===3.
故答案为3.
14.解:∵△ABC∽△DEF,
而△ABC与△DEF对应边的中线的比为2:5,
∴△ABC与△DEF的相似比为2:5,
∴△ABC与△DEF的面积=22:52=4:25.
故答案为4:25.
15.解:设建筑物的高为h米,
则=,
解得h=24.
故答案为:24米.
16.解:∵AD∥BC,AD=2,BC=6,
∴△ADO∽△CBO,
∴==,
∴S△AOD=S△AOB=2.
故答案为2.
三.解答题(共6小题,满分52分)
17.解:(1)①如图所示:△A′B′C′即为所求;
②如图所示:△A″B″C″即为所求;
(2)∵将△ABC作位似变换且缩小为原来的,以y轴为对称轴,将△A′B′C′作轴对称变换,得到△A″B″C″,
∴如果△ABC内一点M的坐标是(x,y),那么经过上述两次变换后其对应点M″的坐标为:(﹣x,y).
故答案为:(﹣x,y).
18.(1)证明:∵BE是△ABC的角平分线,
∴∠ABE=∠CBE.
∵BC=CD,
∴∠CDE=∠CBE=∠ABE.
又∵∠AEB=∠CED,
∴△AEB∽△CED;
(2)解:∵BC=4,BC=CD,
∴CD=4.
∵△CED∽△AEB,
∴=,即=,
∴CE=2.
19.解:过点D作DE⊥AB,
∵同一时刻测得长为0.8m的竹竿影长为1m,
∴=,
则=,
解得:AE=2.56,
故AB=AE+BE=2.56+1.2=3.76(m),
答:旗杆的高度为3.76m.
20.(1)证明:∵AB=AC,
∴∠B=∠C.
∵∠ADE+∠BDE=∠ADB=∠C+∠CAD,
∠ADE=∠C,
∴∠BDE=∠CAD.
∴△BDE∽△CAD.
(2)解:由(1)得.
∵AB=AC=5,BC=8,CD=2,
∴DB=BC﹣CD=6.
∴.
21.证明:(1)∵BD⊥AC,CE⊥AB,
∴∠AEC=∠ADB=90°,
而∠EAC=∠DAB,
∴△AEC∽△ADB,
∴=,
∴=,
而∠EAD=∠CAB,
∴△ADE∽△ABC;
(2)在Rt△AEC中,∠A=60°,
∴∠ACE=30°,
∴AC=2AE,
∵△ADE∽△ABC,
∴=,即=
∴BC=2DE.
22.解:(1)∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴EF=x,
当GH恰好落在边BC上时,
AP+PD=AP+EF=AD,
∴x+x=4,
解得:x=,
∴EF=x=;
故答案为:x,,;
(2)设EH交BC于G,则EM=PD=AD﹣AP=4﹣x,
∵正方形EFGH与△ABC公共部分的面积为6,
∴EF EM=6,
∴x (4﹣x)=6,
解得:x=2,
即AP=2,
当AP=2时,AP<AD,点P在△ABC的内部,满足题意.
一.选择题(共12小题,满分48分)
1.已知2x=3y(y≠0),则下面结论成立的是( )
A.= B.= C.= D.=
2.两个相似三角形的最短边分别为5cm和3cm,他们的周长之差为12cm,那么大三角形的周长为( )
A.14 cm B.16 cm C.18 cm D.30 cm
3.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
4.如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的,得到△COD,则CD的长度是( )
A.2 B.1 C.4 D.2
5.如图,已知l1∥l2∥l3,直线AB分别交l1、l2、l3于A、E、B点,直线CD分别交l1、l2、l3于C、F、D三点,且AE=2,BE=4,则的值为( )
A. B. C. D.2
6.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是( )
A.9.3m B.10.5m C.12.4m D.14m
7.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A.B.C.D.
8.已知AB=2,点P是线段AB上的黄金分割点,且AP>BP,则AP的长为( )
A. B. C. D.
9.如图,线段BD,CE相交于点A,DE∥BC.若AB=4,AD=2,DE=1.5,则BC的长为( )
A.1 B.2 C.3 D.4
10.如图所示,一张矩形纸片ABCD的长AB=acm,宽BC=bcm,E、F分别为AB、CD的中点,这张纸片沿直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比,则a:b等于( )
A.:1 B.1: C.:1 D.1:
11.下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B.∠ADB=∠ABC C.AB2=AD AC D.=
12.如图,在△ABC中,AB=BC=10,AC=12,BO⊥AC,垂足为点O,过点A作射线AE∥BC,点P是边BC上任意一点,连接PO并延长与射线AE相交于点Q,设B,P两点之间的距离为x,过点Q作直线BC的垂线,垂足为R.岑岑同学思考后给出了下面五条结论,正确的共有( )
①△AOB≌△COB;
②当0<x<10时,△AOQ≌△COP;
③当x=5时,四边形ABPQ是平行四边形;
④当x=0或x=10时,都有△PQR∽△CBO;
⑤当时,△PQR与△CBO一定相似.
A.2条 B.3条 C.4条 D.5条
二.填空题(共4小题,满分20分)
13.若(b+d≠0),则= .
14.若△ABC∽△DEF,△ABC与△DEF对应边的中线的比为2:5,则△ABC与△DEF的面积比为 .
15.高4m的旗杆在水平地面上的影子长6m,此时测得附近一个建筑物的影子长36m,则该建筑物的高度是 .
16.如图,在梯形ABCD中,AD∥BC,AD=2,BC=6,若△AOB的面积等于6,则△AOD的面积等于 .
三.解答题(共6小题,满分52分)
17.△ABC在坐标平面内的位置如图所示,请按要求完成下列任务:
(1)画图:①以原点为位似中心,将△ABC作位似变换且缩小为原来的,得到△A′B′C′;
②以y轴为对称轴,将△A′B′C′作轴对称变换,得到△A″B″C″.
(2)填空:如果△ABC内一点M的坐标是(x,y),那么经过上述两次变换后其对应点M″的坐标为 .
18.如图,BE是△ABC的角平分线,延长BE至D,使得BC=CD.
(1)求证:△AEB∽△CED;
(2)若AB=2,BC=4,AE=1,求CE长.
19.如图,一根旗杆AB在某一时刻影子不全落在地面上,有一部分影子落在墙上,测得地面上的影长为3.2m,落在墙上的影长为1.2m,同一时刻测得长为0.8m的竹竿影长为1m,试求出旗杆的高度.
20.已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
21.如图,在△ABC中,∠A=60°,BD⊥AC,垂足为点D,CE⊥AB,垂足为点E.
求证:(1)△ADE∽△ABC.
(2)BC=2DE.
22.如图1,在锐角△ABC中,AD是BC边上的高,BC=6,AD=4,动点P沿线段AD从点A向点D运动,过点P作EF∥BC,EF交AB于E.交AC于F,以EF为边向下作正方形EFGH.
(1)设AP长为x,利用相似三角形的性质.可用含x的代数式表示正方形的边长为EF= ;如图2,当x= 时,GH恰好落在边BC上,此时EF长为 ;
(2)如图3,当GH在△ABC外部,且正方形EFGH与△ABC公共部分的面积为6时,求点P的位置(即求AP的值)
参考答案
一.选择题(共12小题,满分48分)
1.解:A、因为2x=3y,两边都除以2y,得=,故A符合题意;
B、两边除以不同的整式,故B不符合题意;
C、因为2x=3y,两边都除以2y,得=,故C不符合题意;
D、两边除以不同的整式,故D不符合题意;
故选:A.
2.解:根据题意得两三角形的周长的比为5:3,
设两三角形的周长分别为5xcm,3xcm,
则5x﹣3x=12,
解得x=6,
所以5x=30,
即大三角形的周长为30cm.
故选:D.
3.解:3m×2m=6m2,
∴长方形广告牌的成本是120÷6=20元/m2,
将此广告牌的四边都扩大为原来的3倍,
则面积扩大为原来的9倍,
∴扩大后长方形广告牌的面积=9×6=54m2,
∴扩大后长方形广告牌的成本是54×20=1080元,
故选:C.
4.解:∵点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的,得到△COD,
∴C(1,2),则CD的长度是:2.
故选:A.
5.解:∵l1∥l2∥l3,
∴=,
∵AE=2,BE=4,
∴=,
故选:A.
6.解:∵EB∥CD,
∴△ABE∽△ACD,
∴=,即=,
∴CD=10.5(米).
故选:B.
7.解:由正方形的性质可知,∠ACB=180°﹣45°=135°,
A、C、D图形中的钝角都不等于135°,
由勾股定理得,BC=,AC=2,
对应的图形B中的边长分别为1和,
∵=,
∴图B中的三角形(阴影部分)与△ABC相似,
故选:B.
8.解:由于P为线段AB=2的黄金分割点,
且AP>BP,
则AP=×2=﹣1.
故选:B.
9.解:∵DE∥BC,AB=4,AD=2,DE=1.5,
∴,
即,
解得:BC=3,
故选:C.
10.解:∵b:=a:b,
∴a2=2b2,∴a=b,
则a:b=:1.
故选:A.
11.解:A、∵∠ABD=∠ACB,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;
B、∵∠ADB=∠ABC,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;
C、∵AB2=AD AC,∴=,∠A=∠A,△ABC∽△ADB,故此选项不合题意;
D、=不能判定△ADB∽△ABC,故此选项符合题意.
故选:D.
12.解:①∵AB=BC=10,AC=12,BO⊥AC,
∴AO=CO,AB=BC,BO=BO,
∴△AOB≌△COB;
故此选项正确;
②∵AE∥BC,
∴∠AQO=∠OCP,
∵AO=CO,∠AOQ=∠POC,
∴当0<x<10时,△AOQ≌△COP;
故此选项正确;
③当x=5时,
∴BP=PC=5,
∵AQ=PC,
∴AQ=PB=5,
∵AQ∥BC,
∴四边形ABPQ是平行四边形;
故此选项正确;
④当x=0时,P与B重合,
∴∠OBC=∠QPR,
又∵∠BOC=∠PRQ=90°,
∴△BCO∽△PQR;
当x=10时,P与C重合,此时Q与A重合,
∵∠QPR=∠BPO,∠QRP=∠BOC=90°,
∴△QRP∽△BOC,
当x=0时,△BCO∽△PQR与△PQR∽△CBO不相符;故此选项错误;
⑤若△PQR与△CBO一定相似,
则∠QPR=∠BCO,
故OP=OC=6,
过点O作OH⊥BC于H,
由射影定理得CO2=CH CB,
可求得CH=CP=3.6,
故CP=7.2,所以BP=x=2.8
故当时,△PQR与△CBO一定相似.
故此选项正确.
故正确的有4条.
故选:C.
二.填空题(共4小题,满分20分)
13.解:∵==3,
∴a=3b,c=3d,
∴===3.
故答案为3.
14.解:∵△ABC∽△DEF,
而△ABC与△DEF对应边的中线的比为2:5,
∴△ABC与△DEF的相似比为2:5,
∴△ABC与△DEF的面积=22:52=4:25.
故答案为4:25.
15.解:设建筑物的高为h米,
则=,
解得h=24.
故答案为:24米.
16.解:∵AD∥BC,AD=2,BC=6,
∴△ADO∽△CBO,
∴==,
∴S△AOD=S△AOB=2.
故答案为2.
三.解答题(共6小题,满分52分)
17.解:(1)①如图所示:△A′B′C′即为所求;
②如图所示:△A″B″C″即为所求;
(2)∵将△ABC作位似变换且缩小为原来的,以y轴为对称轴,将△A′B′C′作轴对称变换,得到△A″B″C″,
∴如果△ABC内一点M的坐标是(x,y),那么经过上述两次变换后其对应点M″的坐标为:(﹣x,y).
故答案为:(﹣x,y).
18.(1)证明:∵BE是△ABC的角平分线,
∴∠ABE=∠CBE.
∵BC=CD,
∴∠CDE=∠CBE=∠ABE.
又∵∠AEB=∠CED,
∴△AEB∽△CED;
(2)解:∵BC=4,BC=CD,
∴CD=4.
∵△CED∽△AEB,
∴=,即=,
∴CE=2.
19.解:过点D作DE⊥AB,
∵同一时刻测得长为0.8m的竹竿影长为1m,
∴=,
则=,
解得:AE=2.56,
故AB=AE+BE=2.56+1.2=3.76(m),
答:旗杆的高度为3.76m.
20.(1)证明:∵AB=AC,
∴∠B=∠C.
∵∠ADE+∠BDE=∠ADB=∠C+∠CAD,
∠ADE=∠C,
∴∠BDE=∠CAD.
∴△BDE∽△CAD.
(2)解:由(1)得.
∵AB=AC=5,BC=8,CD=2,
∴DB=BC﹣CD=6.
∴.
21.证明:(1)∵BD⊥AC,CE⊥AB,
∴∠AEC=∠ADB=90°,
而∠EAC=∠DAB,
∴△AEC∽△ADB,
∴=,
∴=,
而∠EAD=∠CAB,
∴△ADE∽△ABC;
(2)在Rt△AEC中,∠A=60°,
∴∠ACE=30°,
∴AC=2AE,
∵△ADE∽△ABC,
∴=,即=
∴BC=2DE.
22.解:(1)∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴EF=x,
当GH恰好落在边BC上时,
AP+PD=AP+EF=AD,
∴x+x=4,
解得:x=,
∴EF=x=;
故答案为:x,,;
(2)设EH交BC于G,则EM=PD=AD﹣AP=4﹣x,
∵正方形EFGH与△ABC公共部分的面积为6,
∴EF EM=6,
∴x (4﹣x)=6,
解得:x=2,
即AP=2,
当AP=2时,AP<AD,点P在△ABC的内部,满足题意.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
